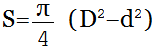Как рассчитать площадь кольца
На данной странице калькулятор поможет рассчитать площадь кольца онлайн. Для расчета задайте внутренние и внешние радиусы или диаметры.
Через радиусы
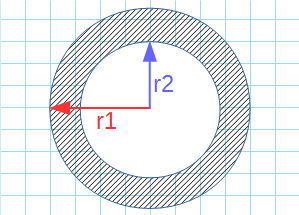
Формула для нахождения площади кольца через внешний и внутренний радиус:
π — константа равная (3.14); r1 — внешний радиус; r2 — внутренний радиус.
Через диаметры
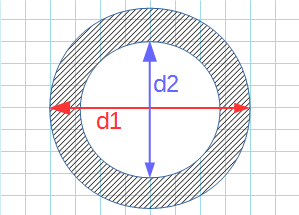
Формула для нахождения площади кольца через внешний и внутренний диаметр:
π — константа равная (3.14); d1 — внешний диаметр; d2 — внутренний диаметр.

{S = pi (R^2 — r^2)}
С помощью приведенных калькулятора и формул можно рассчитать площадь кольца через радиусы или диаметры онлайн.
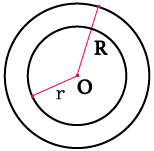
Кольцо — плоская геометрическая фигура, ограниченная двумя концентрическими окружностями.
Содержание:
- калькулятор площади кольца
- формула площади кольца через радиусы
- формула площади кольца через диаметры
- примеры задач
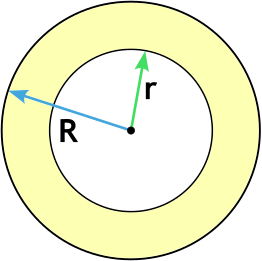
Формула площади кольца через радиусы
{S = pi (R^2 — r^2)}
R — внешний радиус кольца
r — внутренний радиус кольца
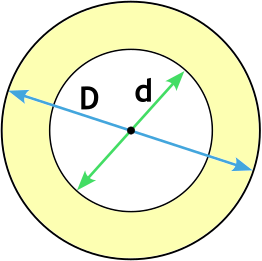
Формула площади кольца через диаметры
{S= dfrac{pi}{4}(D^2 — d^2)}
D — внешний диаметр кольца
d — внутренний диаметр кольца
Примеры задач на нахождение площади кольца
Задача 1
Найдите площадь кольца ограниченного двумя окружностями с общим центром и радиусами 3 см и 7 см.
Решение
В условии задачи даны радиусы ограничивающих кольцо окружностей, поэтому воспользуемся первой формулой.
S = pi (R^2 — r^2) = pi (7^2 — 3^2) = pi (49 — 9) = 40pi approx 125.66371 : см^2
Ответ: 108 cdot 0.866 approx 93.53074 : см^2
Полученный ответ можно проверить с помощью калькулятора .
Задача 2
Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны dfrac{4}{sqrt{pi}} и dfrac{2}{sqrt{pi}}.
Решение
Задача похожа на предыдущую, поэтому алгоритм ее решения будет тот же.
S = pi (R^2 — r^2) = pi ({Big(dfrac{4}{sqrt{pi}} Big) }^2 — {Big(dfrac{2}{sqrt{pi}} Big) }^2) = pi (dfrac{16}{pi} — dfrac{4}{pi}) = pi dfrac{12}{pi} = 12 : см^2
Ответ: 12 : см^2
Наш калькулятор может производить вычисления с выражениями. Для того, чтобы ввести радиусы из условия их нужно записать в понятном для калькулятора формате:
dfrac{4}{sqrt{pi}} : rarr : 4/sqrt(pi)
dfrac{2}{sqrt{pi}} : rarr : 2/sqrt(pi)
Если ввести данные в таком формате, можно проверить ответ .
Задача 3
Найдите площадь кольца образованного двумя окружностями с общим центром если радиусы равны 15 и 13.
Решение
Задача аналогична предыдущим.
S = pi (R^2 — r^2) = pi (15^2 — 13^2) = pi (225 — 169) = 56pi approx 175.92919 : см^2
Ответ: 56pi approx 175.92919 : см^2
Проверка .
Задача 4
Найдите площадь кольца ограниченного двумя окружностями с общим центром и радиусами 13 и 12 см.
Решение
Задача аналогична предыдущим.
S = pi (R^2 — r^2) = pi (13^2 — 12^2) = pi (169 — 144) = 25pi approx 78.53982 : см^2
Ответ: 25pi approx 78.53982 : см^2
Проверка .
При помощи нашего калькулятора вы легко сможете узнать площадь кольца.
Для того что бы вычислить площадь кольца необходимо знать его внутренний и внешний радиус или внутренний и внешний диаметр. Если нам известны указанные величины, для нас не составит труда вычислить площадь кольца.
Площадь кольца рассчитывается по следующим формулам:
- Если нам известен радиус:
Формула для расчета площади кольца через радиус:
S=π(R2-r2) - Если нам известен диаметр:
Формула для расчета площади кольца через диаметр:
S=π/4(D2-d2)
Где S – площадь кольца, R — внешний радиус кольца, r – внутренний радиус кольца, D – внешний диаметр кольца, d — внутренний диаметр кольца, π – число Пи которое всегда примерно равно 3,14.
Площадь кольца
- Главная
- /
- Математика
- /
- Геометрия
- /
- Площадь кольца
Чтобы найти площадь кольца, ограниченного двумя концентрическими окружностями, воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Площадь кольца по радиусам или диаметрам
Чему равна площадь кольца ограниченного двумя окружностями, если:
у внешней окружности
=
у внутренней окружности
=
Ответ: S =
0
Округление числа π: Округление ответа:
Просто введите радиусы или диаметры окружностей, и получите ответ.
Площадь кольца по толщине и любому другому параметру
Чему равна площадь кольца ограниченного двумя окружностями, если:
толщина кольца t =
=
Ответ: S =
0
Округление числа π: Округление ответа:
Просто введите толщину кольца и любой другой известный вам параметр, и получите ответ.
Теория
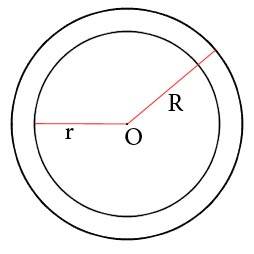
Площадь кольца через радиусы
Чему равна площадь кольца S ограниченного двумя окружностями, если известны радиус внешней окружности R и радиус внутренней окружности r ?
Формула
S = π ⋅ (R² — r²)
Пример
К примеру, определим площадь кольца, у которого внешний радиус R = 3 см, а внутренний радиус r = 2 см:
S = 3.14 ⋅ (3² — 2²) = 3.14 ⋅ (9 — 4) = 3.14 ⋅ 5 = 15.7 см²
Ответ: S = 15.7 см²
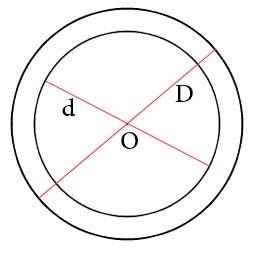
Площадь кольца через диаметры
Чему равна площадь кольца S ограниченного двумя окружностями, если известны диаметр внешней окружности D и диаметр внутренней окружности d ?
Формула
S = π/4 ⋅ (D² — d²)
Пример
К примеру, определим площадь шайбы, внешний диаметр которой D = 4 см, а внутренний – d = 2 см:
S = 3.14 / 4 ⋅ (4² — 2²) = 0.785 ⋅ (16 — 4) = 9.42 см²
Ответ: S = 9.42 см²
Площадь кольца через толщину
Чтобы посчитать площадь кольца S зная его толщину t, необходимо знать ещё какой-нибудь из следующих параметров:
- внешний диаметр D
- внутренний диаметр d
- радиус внешней окружности R
- радиус внутренней окружности r
Формулы
S = π/4 ⋅ (D² — (D — 2t)²)
S = π/4 ⋅ ((d + 2t)² — d²)
S = π ⋅ (R² — (R — t)²)
S = π ⋅ ((r + t)² — r²)
Пример
Для примера, найдём чему равна площадь кольца толщиной t = 2 см и внешним диаметром D = 5 см:
S = 3.14/4 ⋅ (5² — (5 — 2 ⋅ 2)²) = 0.785 ⋅ (25 — 1) = 18.84 см²
См. также
/
/
/ Площадь кольца
Площадь кольца
Площадь кольца вычисляется как разность площадей кругов с радиусами R и r. Также площадь кольца через диаметры находится как произведение одной четвертой числа π на разность квадратов внешнего и внутреннего диаметров кольца.
Установить Площадь кольца на мобильный
Площадь кольца через радиусы
|
||
| Внешний радиус кольца R | ||
| Внутренний радиус кольца r | ||
|
|
||
| Результат |
Площадь кольца через диаметры
|
||
| Внешний диаметр кольца D | ||
| Внутренний диаметр кольца d | ||
| Результат |
Скачать калькулятор
Рейтинг: 2.9 (Голосов 18)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Площадь фигур | Объем фигур | Периметр фигур | Радиус фигур | Единицы измерения площади |
| Конвертеры | Время для пробуждения | Теоремы | Угол | Калькулятор Моей жизни |