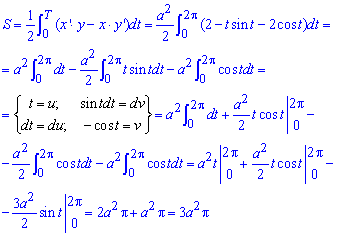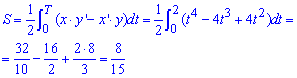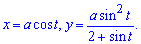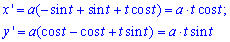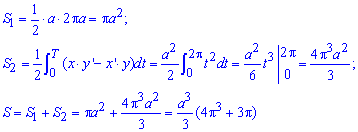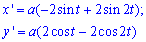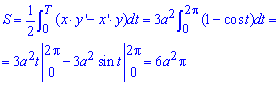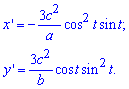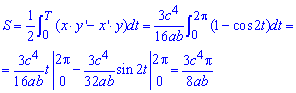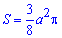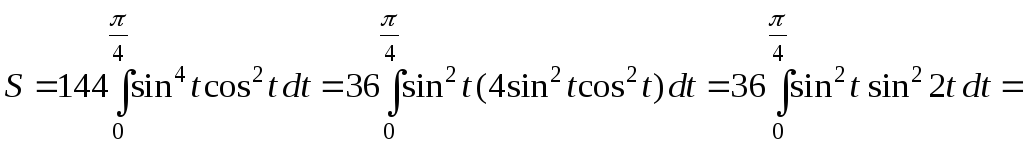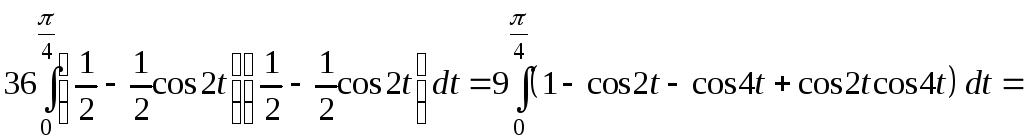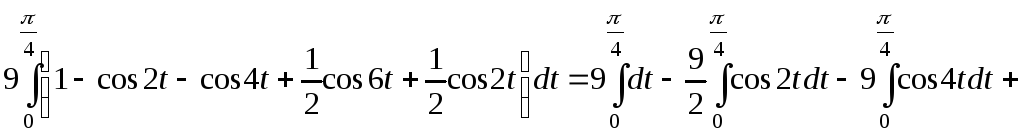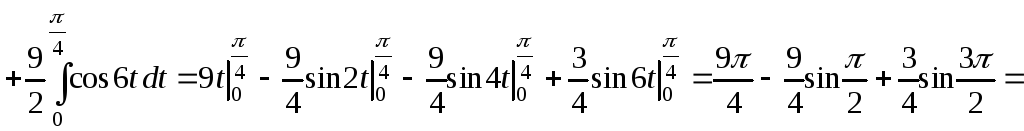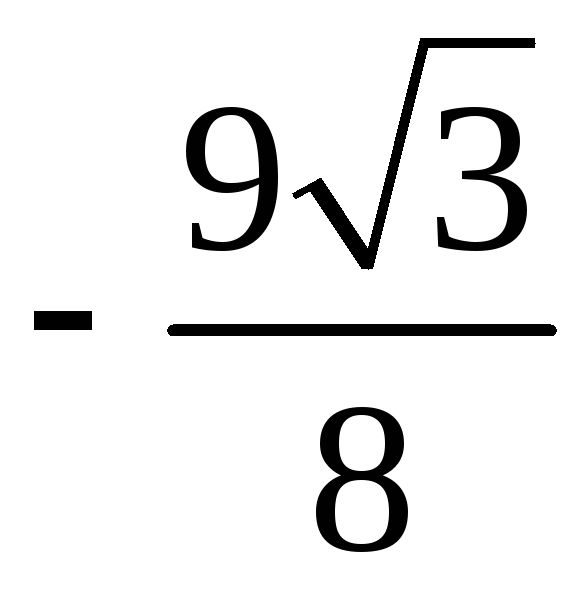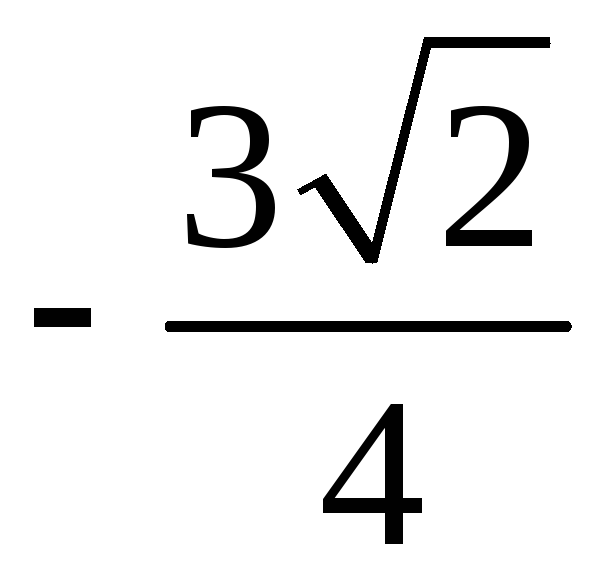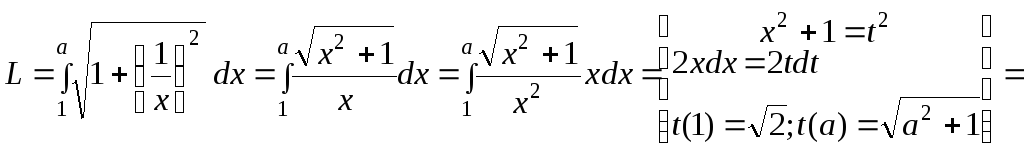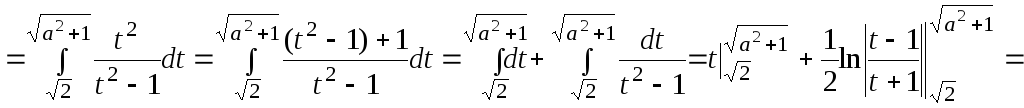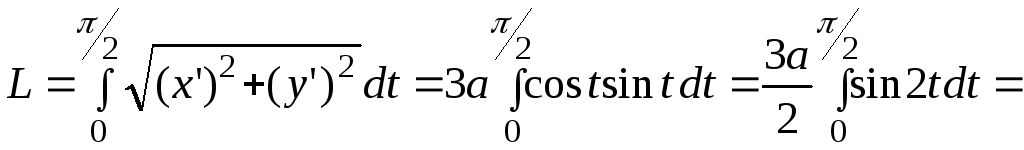Как найти площадь кривой заданной параметрически - Исправление недочетов и поиск решений вместе с Examum.ru

Из настоящей статьи Вы научитесь находить площадь фигуры в пространстве, которая задана параметрическими кривыми.
Для этого Вам нужно знать минимум формул и хорошые знания из интегрирования.
Если имеем x=x(t), y=y(t) — параметрическое уравнение кусково-гладкой простой замкнутой кривой на промежутке [0;T], что проходит против часовой стрелки и ограничивает слева от себя фигурой то ее площадь S находим за формулой
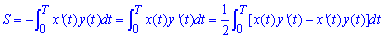
Данный цикл задач в первую очередь облегчит учебу студентам мех-мату Львовского национального университета имени Ивана Франко при прохождении практикума из математического анализа.
Студенты всех Вузов могут набираться практики на подобных интегралах, и изучать методику вычисления площади.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича).

Для запоминания основных моментов схема интегрирования и нахождения площадей из примера в пример будет повторяться. По возможности сами решения будут проиллюстрированы подинтегральными кривыми.

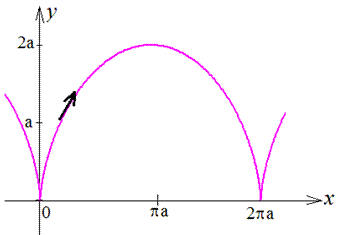
Прибор 2.100 (2413) Найти площадь фигуры, которая ограничена кривыми, заданными в параметрической форме x=a(t-sin(t)), y=a(1-cos(t)) на промежутке [0;2*Pi] и y=0.

Вычисление: Циклоида — плоская трансцендентная кривая, которая определяется кинематически как траектория фиксированной точки круга радиуса a, что катится без скольжения по прямой.
Найдем производные по переменной t заданных функций:
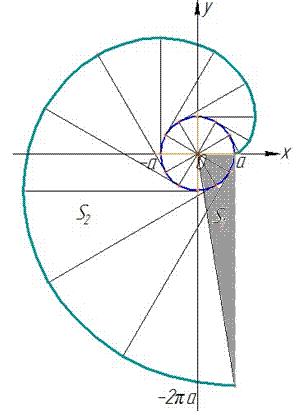
x’=a(1-cos(t));
y’=a*sin(t).
Пределы интегрирования известны по условию — [0;2*Pi].
Запишем подинтегральную функцию за формулой x’*y-x*y’ (поскольку кривая (циклоида) проходит за ходом часовой стрелки):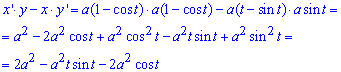
Вычислим площадь фигуры ограниченной одною аркой циклоиды:

Определенные интегралы методом интегрирования частями вычисляются достаточно быстро.
Также не забывайте, что площадь измеряется в единицах квадратных.

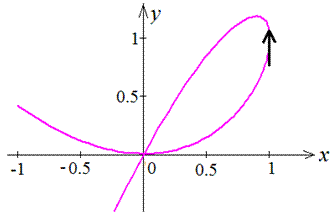
Пример 2.101 (2414) Вычислить площадь фигуры, которая ограничена параметрическими кривыми x=2t-t², y=2t²-t³.

Вычисление: Вычислим производные по переменной t функций:
x’=2-2t;
y’=4t-3t².
Найдем пределы интегрирования — точки пересечения кривой, которая ограничивает заданную фигуру:
x=0 при t₁=0, t₂=2 и
y=0 при t₁=0, t₂=2 .
Поэтому имеем период ровный T=2.
Запишем подинтегральную функцию по формуле x’*y-x*y’ (поскольку кривая проходит против часовой стрелки):

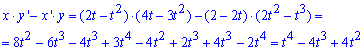
Вычислим площадь фигуры, которая ограничена заданной кривой:

Здесь, как видите, интеграл найти вообще просто, подобные примеры на практических из математического анализа Вы возможно вычисляли огромное количество раз.

Пример 2.102 (2417.1) Найти площадь фигуры, которая ограничена параметрическими кривыми

Вычисление: Продифференцируем функции по переменной t:

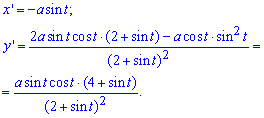
Запишем пределы интегрирования (нужно предварительно исследовать функцию):
T=[0;2*Pi].
Запишем подинтегральную функцию за формулой x’*y

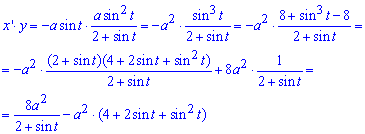
Вычислим площадь фигуры по формуле для параметрических кривых:

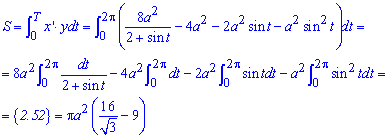
Определенный интеграл достаточно простой в плане вычислений.

Пример 2.103 (2415) Найти площадь фигуры, ограниченной кривыми
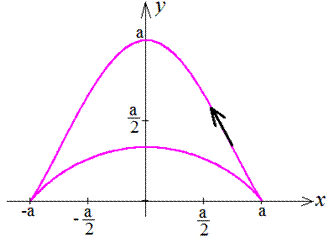
x=a(cos(t)+t*sin(t)), y=a(sin(t)-t*cos(t)) (развертка круга) и x=a, .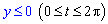

Вычисление: Найдем производные функций по переменной t:

Пределы интегрирования выписываем из начального условия — [0;2*Pi].
Выведем подинтегральную функцию за формулой x’*y-x*y’

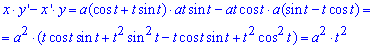
Вычислим площадь фигуры, которая ограничена заданной кривой и прямыми:

Следует заметить, что при интегрировании по углу не учитывается площадь треугольника S₁, что заштрихована серым.
Без построения графика функции учесть необходимость находить дополнительную площадь достаточно трудно.

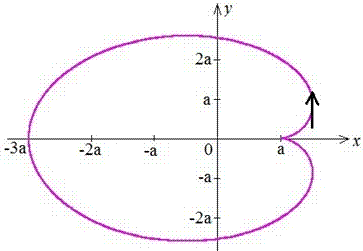
Пример 2.104 (2416) Найти площадь фигуры, ограниченной кривыми
x=a(2*cos(t)-cos(2t)), y=a(2*sin(t)-sin(2t)).

Вычисление: Вычислим производные по переменной t функций:

Запишем пределы интегрирования: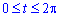
Сложим уравнение подинтегральной функции по формуле x’*y-x*y’

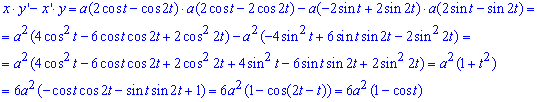
Через определенный интеграл вычисляем площадь фигуры, которая ограничена заданной кривой:

Интеграл не сложный, а конечная формула простая для расчетов площади.

Пример 2.105 (2417) Найти площадь фигуры, ограниченной параметрическими кривыми 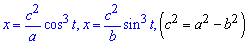(эволюта эллипса)

Вычисление: Эволюта — множество точек центров кривизны кривой.
По отношению к своей эволюте любая кривая является эвольвентой (інволютою, то есть разверткой этой кривой).
Найдем производные функций по переменной t :

Пределы интегрирования равны:

Запишем подинтегральную функцию по формуле
x’*y-x*y’:

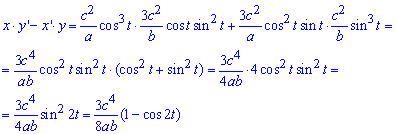
Интегрированием за периодом находим площадь фигуры, которая ограничена заданной кривой:

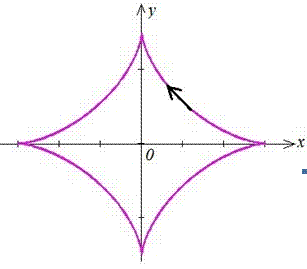
Пример 2429 Возведя уравнение к параметрическому виду, найти площади фигуры, ограниченной кривой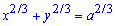 (астроида).
Вычисление: Перепишем уравнение астроиды в виде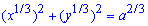

Пусть x=a*cos³(t), y=a*sin³(t).
Нетрудно подставить и убедиться, что это именно та подстановка которая будет уравнением астроиды в параметрической форме.
Далее по аналогии с примером 2.105 будем иметь

В следующих публикациях Вы найдете больше примеров на нахождение площади фигуры с помощью определенного интеграла.

Источник

Если фигура
ограничена кривой, заданной параметрическими
уравнениями
,
прямымии осью9рис. 5), то площадь ее вычисляется по
формулам:

(42)

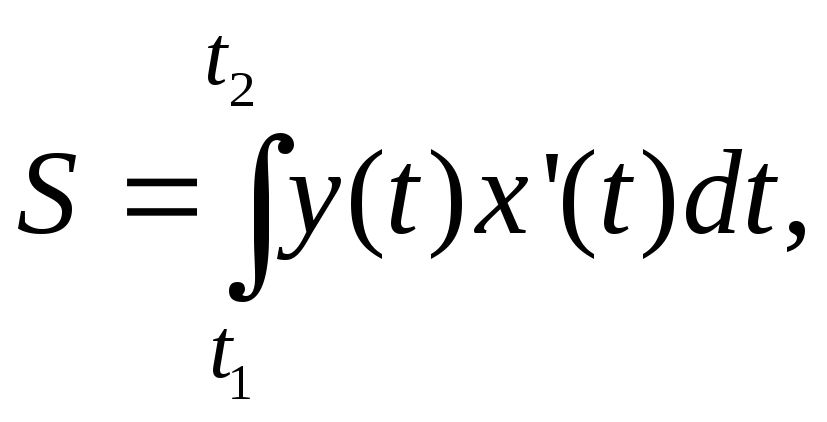
а пределы
интегрирования находятся из уравнений
на отрезка.
Порядок вычисления аналогичен п. 2.9.1.

Пример. Найти
площадь фигуры, ограниченной линиями,
заданными уравнениями:.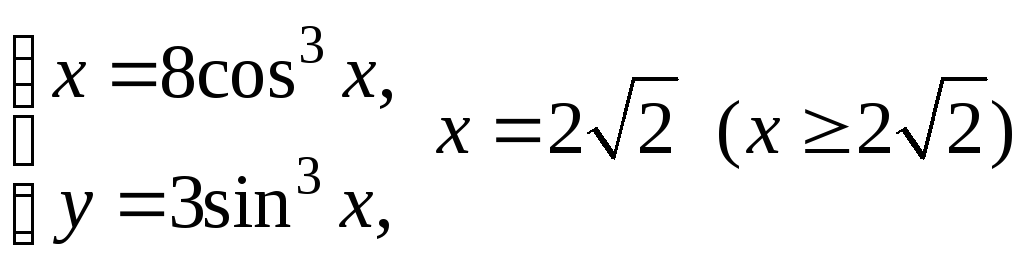

Решение.
Построим кривую, заданную параметрическими
уравнениями (рис. 5). Для этого вычислим
значения
ии поместим их в табл. 5.

ОТРЕДАКТИРОВАТЬ

Таблица 5

Вспомогательная таблица для построения параметрически заданной кривой

Мы подставляли
значения
из верхней строки таблицы в параметрические
уравнения и последовательно получали
значенияи.
Построим также и прямую(см. рис. 6). Найдем пределы интегрирования.
Приравняем,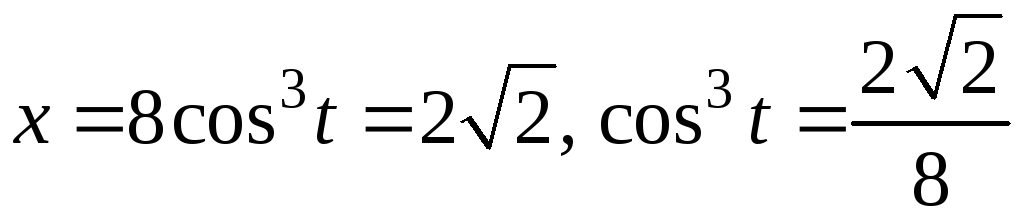
отсюда.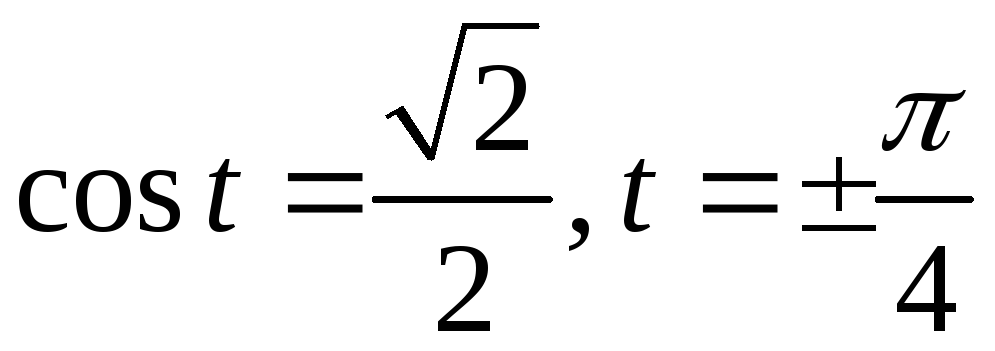
Посколькуизменяется отдо.
Так как фигура, площадь которой мы хотим
навйти, симметрична относительно оси,
то можно интегрировать отдо.
А результат затем удвоить. Подставляем
в формулу (42)::

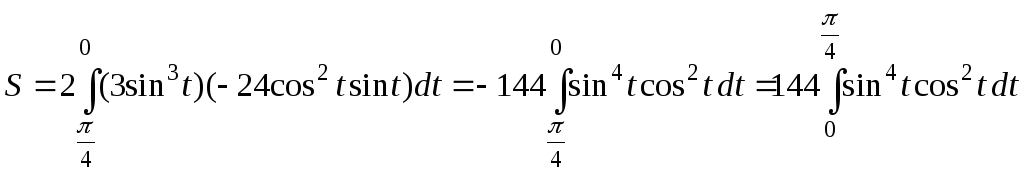
Для вычисления
интеграла воспользуемся формулами
(22)-(27) из п. 1.7:

2.9.3. Площадь фигуры, ограниченной кривой, заданной в полярных координатах

Пусть кривая задана
в полярных координатах уравнением
и двумя лучамии,
тогда ее площадь (рис. 7) вычисляется по
формуле:

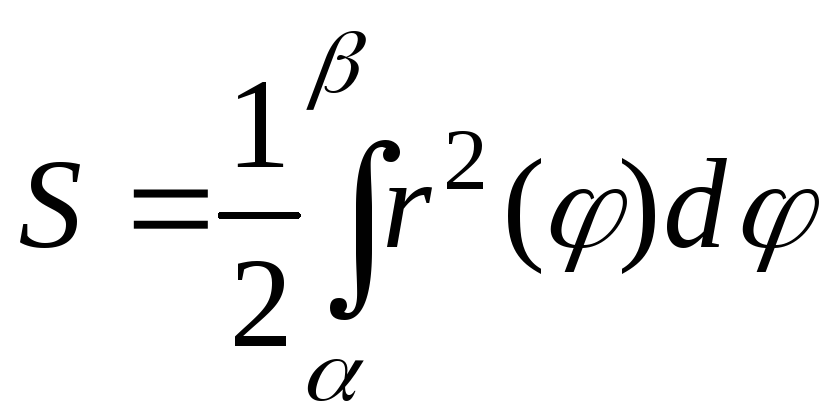
(43)

Порядок вычислений
аналогичен п. 2.9.1.

Пример. Найти
площадь фигуры, ограниченной линией
,
перейдя предварительно к полярным
координатам.

Решение. Переход
от декартовых к полярным координатам
осуществляется по формулам: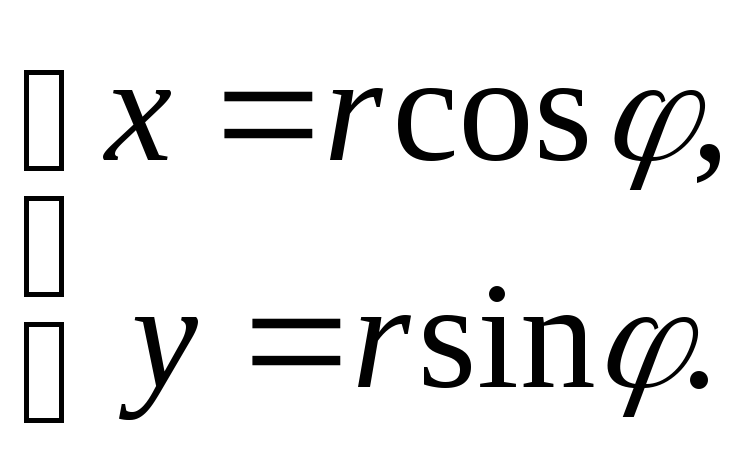Подставив эти выражения в уравнение
кривой, получим:или.
Отсюда получаем уравнение кривой в
полярных координатах:.

Поскольку в правой
части уравнения стоит неотрицательная
величина, то полярный угол может принимать
любые значения
.
В силу периодичности функциивычислим подробно таблицу значений для
аргументов в промежутке(табл. 6).

Таблица 6

Вспомогательная таблица для построения кривой, заданной в полярных координатах

Построим эту кривую
( четырехлепестковую розу). В силу
симметрии фигуры достаточно проинтегрировать
по
отдо,
а затем результат умножить на 8.

Применим формулу
(43):
.
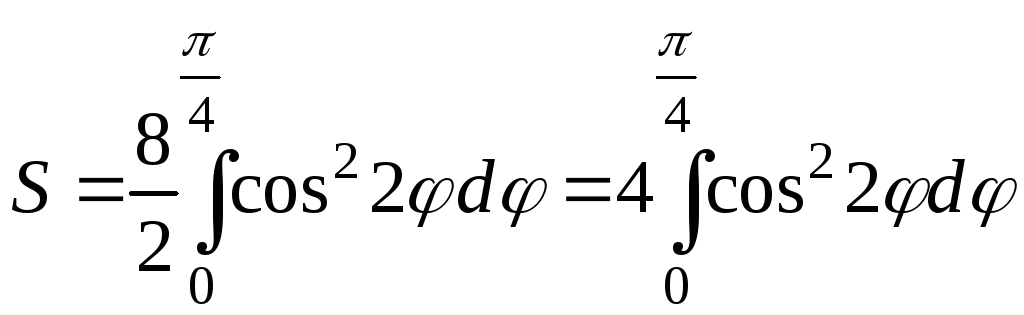
Для вычисления интеграла воспользуемся
формулой понижения степени (15) из п. 1.7:.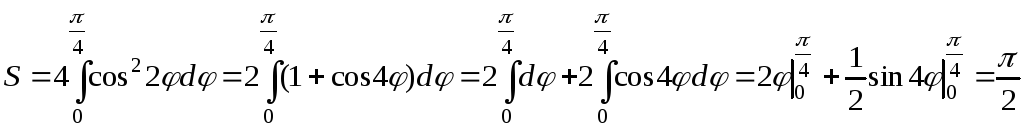

Вычислить интеграл
непосредственно зачастую весьма
непросто. Поэтому создаются специальные
таблицы интегралов. При затруднениях
в вычислении того или иного интеграла,
полученного при решении конкретной
технической задачи, можно ими
воспользоваться. Есть класс так называемых
«неберущихся» интегралов, т.е. класс
функций, первообразные для которых не
являются элементарными. Тем не менее,
интегралы от таких функций часто
встречаются в математике и приложениях.
Так, в теории вероятностей мы встретимся
с функцией
,
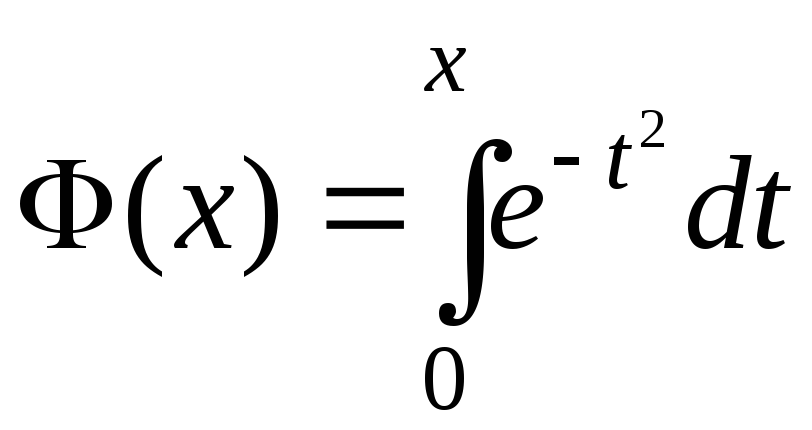
выражающейся через такой «неберущийся»
интеграл. Такого рода интегралы
встречаются в электротехнике, оптике
и т.д.

Для вычисления
таких интегралов разработаны специальные
методы. Например, формулы прямоугольников,
трапеций, Симпсона или с помощью рядов.

Определенный
интеграл применяется в математике для
нахождения длин дуг кривых, объемов
различных тел, площади поверхности тел
вращения и др. Широко применяется
определенный интеграл в механике и
физике. Это вычисление статических
моментов, моментов инерции плоских дуг
кривых и фигур, координат центра тяжести,
а также вычисление работы, давления и
многого другого.

Приложение.

Вычисление
длины кривой, заданной явным уравнением.

Если кривая задана
явным уравнением в прямоугольных
декартовых координатах

то
.

(1)

Пример.

Вычислить
длину дуги куска графика логарифмической
функции
.

Решение. Подставляя
в формулу (1)
,
получим:

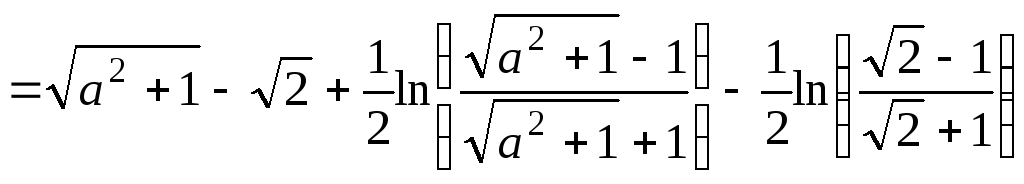
Вычисление
длины кривой, заданной параметрическим
уравнением.

Если кривая задана
параметрическим уравнением в прямоугольных
декартовых координатах

то.
(2)

Пример.
Найти длину
дуги четверти астроиды
между точкамии.

Решение. Найдем
вначале пределы интегрирования из
уравнений:
,.
Отсюда.
Вычислим также элементы подкоренного
выражения:.
Преобразуем подынтегральное выражение,
используя основное тригонометрическое
тождество:.
Подставив полученное выражение и пределы
интегрирования в формулу (2), окончательно
получаем выражение для длины дуги
четверти астроиды:

Вычисление
длины кривой, заданной уравнением в
полярных координатах.

Если кривая задана
уравнением в полярных координатах

то.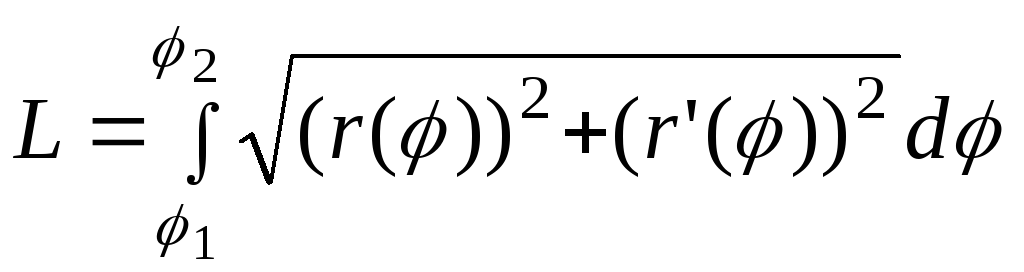

(3)

Пример.
Вычислить
длину дуги одного витка логарифмической
спирали
,
где.

Решение. Подставим
ив формулу (3), получим:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Вычисление площадей фигур в различных системах координат

Площадь плоской фигуры в декартовых координатах

Напомним, что мы назвали криволинейной трапецией фигуру, ограниченную осью абсцисс, прямыми x=a и x=b и графиком функции y=f(x) . В этом пункте выведем формулу для вычисления площади криволинейной трапеции.

Теорема 3. Если функция y=f(x) неотрицательна на отрезке [a;b] и непрерывна на нем, то соответствующая ей криволинейная трапеция квадрируема, причем ее площадь выражается формулой

${ S= intlimits_{a}^{b} f(x),dx,.}$

(4)

Доказательство. Криволинейная трапеция ограничена тремя отрезками и графиком непрерывной функции y=f(x) . Как было показано в пункте 2 такая фигура квадрируема. Чтобы вычислить площадь этой трапеции, построим для нее внешние и внутренние ступенчатые фигуры (см. рис. 26).

Тогда, с одной стороны, имеем:

$sum_{k=0}^{n-1}m_kDelta x_kleqslant Sleqslant sum_{k=0}^{n-1} M_kDelta x_k,,$

где $sum_{k=0}^{n-1}m_kDelta x_k$ — площадь внутренней ступенчатой фигуры, $sum_{k=0}^{n-1}M_kDelta x_k$ —площадь внешней ступенчатой фигуры, $m_k=min_{xin [x_k;x_{k+1}]}f(x)$ и $M_k=max_{xin[x_k;x_{k+1}]}f(x)$ . С другой стороны, по определению интеграла можно записать:

$sum_{k=0}^{n-1}m_kDelta x_kleqslant intlimits_{a}^{b} f(x),dxleqslant sum_{k=0}^{n-1}M_kDelta x_k,.$

Таким образом, числа и $intlimits_{a}^{b} f(x),dx$ разделяют одни и те же числовые множества: $Biggl{,sum_{k=0}^{n-1}m_kDelta x_k,Biggr},$ $Biggl{,sum_{k=0}^{n-1}M_kDelta x_k,Biggr}$ . Но, как было показано при изучении определенного интеграла, эти множества разделяются лишь одним числом, и потому $S=intlimits_{a}^{b} f(x),dx$ . Теорема доказана.

Аналогично доказывается, что если фигура ограничена снизу графиком функции y=f_1(x) , сверху графиком функции y=f_2(x) , а слева и справа прямыми x=a,~x=b (рис. 30), то ее площадь выражается формулой

$S= intlimits_{a}^{b}bigl[f_2(x)-f_1(x)bigr]dx,.$

Наглядный смысл формулы (4) состоит в том, что криволинейную трапецию можно рассматривать как объединение «бесконечно тонких полосок» с основаниями и высотами f(x) .

Площадь фигуры между двумя графиками функций

Пусть теперь функция y=f(x) непрерывна на отрезке [a;b] и принимает на нем только неположительные значения. Выразим с помощью определенного интеграла площадь соответствующей криволинейной трапеции .

Рассмотрим фигуру Phi , симметричную фигуре относительно оси . Эта фигура (рис. 31) представляет собой криволинейную трапецию, ограниченную сверху графиком непрерывной на отрезке [a;b] функции y=f(x) , которая на [a;b] принимает только неотрицательные значения. По доказанному выше

Интегрирование знакопеременной функции

$S(Phi)= intlimits_{a}^{b} bigl(-f(x)bigr)dx$ . Но S(Phi)=S(F).

Значит,

$S(F)= intlimits_{a}^{b} bigl(-f(x)bigr)dx= -intlimits_{a}^{b} f(x),dx,.$

Как мы видим, в рассматриваемом случае интеграл $intlimits_{a}^{b} f(x),dx$ дает значение площади криволинейной трапеции с точностью до знака. Если же функция меняет знак на отрезке [a;b] в конечном числе точек, то значение интеграла $intlimits_{a}^{b} f(x),dx$ дает алгебраическую сумму площадей соответствующих криволинейных трапеций, ограниченных частями графика функции y=f(x) , отрезками оси и, быть может, отрезками, параллельными оси (рис. 32).

Пример 1. Найти площадь фигуры, ограниченной кривой y=e^x , осью абсцисс и прямыми x=1,~x=2 (рис. 33).

Решение. Имеем: $S= intlimits_{1}^{2} e^x,dx= Bigl.{e^x}Bigr|_{1}^{2}= e^2-e= e(e-1)$ (кв. ед.).

Пример 2. Вычислить площадь фигуры, ограниченной дугой параболы y^2=4x и отрезком прямой x=2 (рис. 34).

Решение. Из рисунка видно, что трапеция, площадь которой нужно найти, расположена симметрично относительно оси абсцисс и, следовательно, искомая площадь равна

$S= 2int_{0}^{2}2sqrt{x},dx= left.{frac{4x^{3/2}}{3/2}}right|_{0}^{2}= frac{8}{3}cdot 2^{3/2}= frac{16}{3}sqrt{2},.$

Пример 3. Найти площадь фигуры, ограниченной графиками функций y^2=9x,~ y=3x (рис. 35).

Решение. Искомая площадь равна разности площадей криволинейного треугольника OAB и прямоугольного треугольника OAB:

$S= intlimits_{0}^{1} sqrt{9x},dx- intlimits_{0}^{1} 3x,dx= left.{3cdot frac{x^{3/2}}{3/2}}right|_{0}^{1}- left.{3cdot frac{x^2}{2} }right|_{0}^{1}= 2-frac{3}{2}= frac{1}{2},.$

Площадь фигуры, ограниченной кривой, осью абсцисс и двумя прямыми

Пример 4. Вычислить площадь фигуры, ограниченной петлей кривой a(y^2-x^2)+x^3=0 .

Решение. Из уравнения кривой видно, что она расположена симметрично относительно оси . Следовательно, можно сначала вычислить половину искомой площади (рис. 36). Рекомендуем читателю подробно исследовать и построить данную кривую.

Площадь фигуры, ограниченной петлёй кривой

Записав уравнение кривой в виде $y^2=frac{x^2}{a}(a-x)$ , найдем точки пересечения ее с осью , положив y=0colon, x_1=0,~ x_2=a . Учитывая сказанное, найдем площадь половины петли:

$frac{1}{2}S= frac{1}{sqrt{a}} intlimits_{0}^{a} xsqrt{a-x},dx,.$

Воспользовавшись формулой из таблицы при a=-1,~ b=a , получим:

$intlimits_{0}^{a} xsqrt{a-x},dx= left.{frac{2(-3x-2a)sqrt{(a-x)^3}}{15}}right|_{0}^{a}= frac{4}{15},a^{5/2},.$

Значит, окончательно имеем:

$frac{1}{2}S= frac{1}{sqrt{a}}cdot frac{4}{15},a^{5/2}= frac{4}{15},a^2quad Leftrightarrowquad S=frac{8}{15},a^2,.$

Площадь фигуры, ограниченной кривой, заданной параметрически

Пусть кривая y=f(x),~ f(x)geqslant0,~ aleqslant xleqslant b задана в параметрической форме

$begin{cases}x=varphi(t),\ y=psi(t),end{cases} alpha leqslant tleqslant b,,$

где функция x=varphi(t) монотонна на отрезке [alpha;beta] , причем varphi(alpha)=a, varphi(beta)=b , и имеет на этом отрезке непрерывную производную. Так как y=f(x)= fbigl(varphi(t)bigr)= psi(t) , то по формуле замены переменной под знаком определенного интеграла получаем:

$S= intlimits_{a}^{b} f(x),dx= intlimits_{alpha}^{beta} fbigl(varphi(t)bigr) varphi'(t),dt= intlimits_{alpha}^{beta} psi(t) varphi'(t),dt,.$

Итак, площадь фигуры, ограниченной кривой, заданной параметрически, вычисляется по формуле:

$S= intlimits_{alpha}^{beta} psi(t)varphi'(t),dt,.$

(5)

Пример 5. Вычислить площадь эллипса, заданного параметрически $begin{cases} x=acos{t},,\ y=bsin{t},,end{cases} 0leqslant tleqslant 2pi,.$

Площадь фигуры, ограниченной эллипсом

Решение. Выберем ту часть эллипса (рис. 37), которая расположена в первом квадранте. Точке A(a;0) соответствует значение t=0 , а точке B(0;b) — значение $t=frac{pi}{2}$ . Поэтому

$begin{aligned} S&= 4intlimits_{0}^{a}y,dx= -4intlimits_{0}^{pi/2}bsin{t}cdot(-asin{t}),dt= 4abintlimits_{0}^{pi/2} sin^2t,dt=\ &= 2abintlimits_{0}^{pi/2} bigl(1-cos2tbigr),dt= left.{2ab!left(t- frac{1}{2}sin2t right)}right|_{0}^{pi/2}= pi,ab,. end{aligned}$

Площадь фигуры, заданной в полярных координатах

Вычислить площадь сектора, ограниченного лучами ell и , выходящими из точки , и непрерывной кривой Gamma (рис. 38). Выберем полярную систему координат, полюсом которой является точка . Пусть rho=rho(varphi) — полярное уравнение кривой Gamma , а varphi_0 и Phi — углы между полярной осью и лучами ell и соответственно. При этом пусть функция непрерывна на [varphi_0;Phi] .

Разобьем данный сектор на частей лучами

$varphi_0< varphi_1< varphi_2< ldots< varphi_k< varphi_{k+1}< ldots< varphi_n= Phi$

и рассмотрим k-й частичный сектор $[varphi_k; varphi_{k+1}]$ (рис. 39). Пусть r_k — наименьшее значение функции rho(varphi) в $[varphi_k; varphi_{k+1}]$ , a R_k — наибольшее значение функции в этом отрезке.

Площадь в полярных координатах и разбиение сектора на n частей

Построим два круговых сектора с радиусами r_k и R_k . Обозначим через Deltavarphi_k величину угла рассматриваемого частичного сектора. Тогда площадь частичного криволинейного сектора будет заключена между площадями вписанного и описанного частичных круговых секторов

$frac{1}{2}cdot r_k^2cdot Deltavarphi_k leqslant S_kleqslant frac{1}{2}cdot R_k^2cdot Deltavarphi_k,.$

Построим аналогичным образом внутренние и внешние круговые секторы для всех частичных криволинейных секторов. Объединяя их, получим внутреннюю и внешнюю фигуры.

Площадь внутренней фигуры, состоящей из круговых секторов, равна $frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_k$ , а площадь внешней фигуры равна — $frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k$ . Эти выражения являются нижней и верхней суммами Дарбу s_P и S_P для интеграла $frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi$ . Так как функция rho(varphi) непрерывна, то непрерывна, а потому и интегрируема функция . Поэтому для любого varepsilon найдется такое разбиение отрезка [varphi_0,Phi] , что S_P-s_P<varepsilon . Из теоремы 2 пункта 2 следует, что заданный криволинейный сектор квадрируем. При этом для его площади выполняются неравенства

Площадь, ограниченная одним лепестком полярной розы

$frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_kleqslant Sleqslant frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k,.$

(6)

В то же время по определению определенного интеграла

$frac{1}{2} sum_{k=0}^{n-1} r_k^2 Deltavarphi_kleqslant frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi leqslant frac{1}{2} sum_{k=0}^{n-1} R_k^2 Deltavarphi_k,.$

(7)

В силу единственности разделяющего числа из неравенств (6) и (7) следует, что

$S= frac{1}{2} intlimits_{varphi_0}^{Phi} rho^2(varphi),dvarphi,.$

(8)

Пример 6. Вычислить площадь, ограниченную одним лепестком розы rho=asin2varphi (рис. 40).

Решение. Значениям varphi=0 и $varphi=frac{pi}{2}$ соответствует rho=0 Поэтому

$S= frac{1}{2} intlimits_{0}^{pi/2} a^2sin^22varphi,dvarphi= frac{a^2}{2} intlimits_{0}^{pi/2} frac{1-cos4varphi}{2},dvarphi= left.{frac{a^2}{4}! left(varphi- frac{1}{4}sin4varphiright)}right|_{0}^{pi/2}= frac{a^2}{4}cdot frac{pi}{2}= frac{pi}{2},a^2,.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник