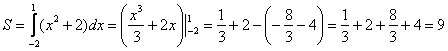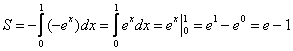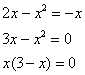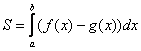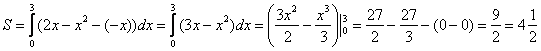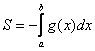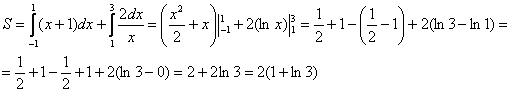Площадь поверхности
разделов
от теории до практики
примеров
Примеры решения задач
видео
Примеры решения задач
-
Первая квадратичная форма поверхности.
Начать изучение
-
Площадь простой поверхности.
Начать изучение
-
Площадь почти простой поверхности.
Начать изучение
Первая квадратичная форма поверхности.
Пусть простая поверхность задана векторным уравнением
$$
boldsymbol{r} = boldsymbol{r}(u, v), (u, v) in overline{Omega},label{ref1}
$$
где (Omega) плоская область.
Найдем скалярный квадрат вектора
$$
dboldsymbol{r} = boldsymbol{r}_{u}(u, v) du + boldsymbol{r}_{v}(u, v) dv.nonumber
$$
Полагая
$$
E = (boldsymbol{r}_{u}, boldsymbol{r}_{u}),quad F = (boldsymbol{r}_{u}, boldsymbol{r}_{v}),quad G = (boldsymbol{r}_{v}, boldsymbol{r}_{v}),label{ref2}
$$
получаем, что справедлива формула
$$
|dboldsymbol{r}|^{2} = (dboldsymbol{r}, dboldsymbol{r}) = E(u, v) du^{2} + 2F(u, v) du dv + G(u, v) dv^{2}.label{ref3}
$$
Выражение, стоящее в правой части равенства eqref{ref3}, называется первой квадратичной формой поверхности, числа (E), (F) и (G) называются коэффициентами первой квадратичной формы поверхности.
Лемма 1.
Первая квадратичная форма простой поверхности положительно определена, то есть (|dboldsymbol{r}|^{2} > 0), если ((du)^{2} + (dv)^{2} > 0).
Доказательство.
(circ) Так как
$$
(boldsymbol{a}, boldsymbol{b}) = |boldsymbol{a}| cdot |boldsymbol{b}| cos widehat{boldsymbol{ab}},quad |[boldsymbol{a}, boldsymbol{b}]| = |boldsymbol{a}| cdot |boldsymbol{b}| cdot |sin widehat{boldsymbol{ab}}|,nonumber
$$
то справедливо тождество
$$
|[boldsymbol{a}, boldsymbol{b}]|^{2} = |boldsymbol{a}|^{2} cdot |boldsymbol{b}|^{2}-|(boldsymbol{a}, boldsymbol{b})|^{2},nonumber
$$
Подставляя в это тождество (boldsymbol{a} = boldsymbol{r}_{u}), (boldsymbol{b} = boldsymbol{r}_{v}), и пользуясь тем, что в любой точке простой поверхности векторы (boldsymbol{r}_{u}) и (boldsymbol{r}_{v}) неколлинеарны, получаем
$$
|[boldsymbol{r}_{u}, boldsymbol{r}_{v}]|^{2} = EG-F^{2} > 0.nonumber
$$
Условия (E > 0), (G > 0), (EG-F^{2} > 0) достаточны для положительной определенности первой квадратичной формы поверхности. (bullet)
Говорят, что первая квадратичная форма задает на поверхности метрику. Зная коэффициенты первой квадратичной формы поверхности, можно вычислить длины кривых, лежащих на поверхности, определить площадь поверхности. Например, дифференциалы длин дуг координатных кривых, проходящих через точку (A(u, v)) поверхности, равны следующим величинам:
$$
ds_{1} = |boldsymbol{r}_{u}du| = sqrt{E}|du|,quad ds_{2} = |boldsymbol{r}_{v}dv| = sqrt{G}|dv|.label{ref4}
$$
Площадь простой поверхности.
Пусть простая поверхность задана уравнением eqref{ref1}. Рассмотрим на поверхности криволинейный параллелограмм, ограниченный координатными линиями (u), (u + Delta u), (v), (v + Delta v). Векторы (boldsymbol{r}_{u}(u, v)Delta u) и (boldsymbol{r}_{v}(u, v)Delta v) будут касательными к координатным линиям, проходящим через точку (A(u, v)) поверхности (рис. 53.1), а длины этих векторов в силу формул eqref{ref4} будут отличаться от длин сторон криволинейного параллелограмма на (o(Delta u)) и (o(Delta v)) соответственно при (Delta u rightarrow 0), (Delta v rightarrow 0). Поэтому естественно считать, что площадь криволинейного параллелограмма приближенно равна площади (dS) параллелограмма, построенного на векторах (boldsymbol{r}_{u} Delta u) и (boldsymbol{r}_{v} Delta v). Таким образом, при (Delta u > 0), (Delta v > 0).
$$
dS = |[boldsymbol{r}_{u}, boldsymbol{r}_{v}] Delta u Delta v| = sqrt{EG-F^{2}} du dv.label{ref5}
$$
Выражение eqref{ref5} называется элементом площади поверхности.
Определим формально площадь простой поверхности (Sigma) как следующий двойной интеграл (область (Omega) предполагается измеримой по Жордану):
$$
S(Sigma) = iintlimits_{Omega} |[boldsymbol{r}_{u}, boldsymbol{r}_{v}]| du dv = iintlimits_{Omega} sqrt{EG-F^{2}} du dv.label{ref6}
$$
Это определение оправдано приведенными выше эвристическими рассуждениями, а также перечисленными ниже свойствами площади поверхности.
Свойство 1.
Число (S(Sigma)) не зависит от способа параметризации поверхности.
Доказательство.
(circ) Пусть переход от параметрического уравнения eqref{ref1} к параметрическому уравнению
$$
boldsymbol{rho} = boldsymbol{rho}(u’, v’), (u’, v’) in Omega’,nonumber
$$
совершается при помощи взаимно однозначного и непрерывно дифференцируемого отображения области (Omega’) на область (Omega) с якобианом, не равным нулю. Тогда, воспользовавшись формулой отсюда и формулой замены переменных в двойном интеграле, получаем
$$
S(Sigma) = iintlimits_{Omega’} |[boldsymbol{rho}_{u’}, boldsymbol{rho}_{v’}]| du’ dv’ = iintlimits_{Omega’} |[boldsymbol{r}_{u}, boldsymbol{r}_{v}]| cdot left|frac{partial(u, v)}{partial(u’, v’)}right| du’ dv’ = iintlimits_{Omega} |[boldsymbol{r}_{u}, boldsymbol{r}_{v}]| du dv. bulletnonumber
$$
Свойство 2.
Если поверхность (Sigma) есть плоская измеримая по Жордану область (Omega), заданная уравнениями
$$
x = u, y = v, z = 0, (u, v) in Omega,nonumber
$$
то ее площадь, вычисленная при помощи формулы eqref{ref6}, совпадает с плоской мерой Жордана области (Omega).
Доказательство.
(circ) Так как
$$
boldsymbol{r} = (u, v, 0), boldsymbol{r}_{u} = (1, 0, 0), boldsymbol{r}_{v} = (0, 1, 0), E = G = 1,nonumber F = 0,
$$
то
$$
S(Sigma) = iintlimits_{Omega} |[boldsymbol{r}_{u}, boldsymbol{r}_{v}]| du dv = iintlimits_{Omega} du dv = m(Omega). bulletnonumber
$$
Свойство 3.
Выражение (S(Sigma)) аддитивно зависит от поверхности.
Доказательство.
(circ) Если область (Omega) гладкой перегородкой разбита на области (Omega_{1}) и (Omega_{2}), то и поверхность (Sigma) разобьется на простые поверхности (Sigma_{1}) и (Sigma_{2}). Из аддитивности двойного интеграла по области интегрирования следует, что
$$
S(Sigma) = S(Sigma_{1}) + S(Sigma_{2}). bulletnonumber
$$
Свойство 4.
Для поверхности, являющейся графиком непрерывно дифференцируемой функции на замыкании измеримой по Жордану области (Omega), формула eqref{ref6} для площади поверхности имеет следующий вид:
$$
S(Sigma) = iintlimits_{Omega} sqrt{1 + f_{x}^{2} + f_{y}^{2}} dx dy.label{ref7}
$$
Доказательство.
(circ) Действительно, так как
$$
boldsymbol{r} = (x, y, f(x, y)), boldsymbol{r}_{x} = (1, 0, f_{x}(x, y)), boldsymbol{r}_{y} = (0, 1, f_{y}(x, y)),nonumber
$$
то
$$
E = boldsymbol{r}_{x}^{2} = 1 + f_{x}^{2}, F = (boldsymbol{r}_{x}, boldsymbol{r}_{y}) = f_{x}f_{y}, G = boldsymbol{r}_{y}^{2} = 1 + f_{y}^{2},nonumber
$$
$$
EG-F^{2} = (1 + f_{x}^{2})(1 + f_{y}^{2})-f_{x}^{2}f_{y}^{2} = 1 + f_{x}^{2} + f_{y}^{2}. bulletnonumber
$$
Пример 1.
Найти площадь части сферы (x^{2} + y^{2} + z^{2} = a^{2}), вырезаемой из нее цилиндром (x^{2}-ax + y^{2} = 0) (см. рис. 48.10).
Решение.
(triangle) В силу симметрии достаточно ограничиться рассмотрением той части сферы, которая лежит в первом октанте. Цилиндр будет вырезать из нее множество точек, определяемое следующими неравенствами и равенствами:
$$
x^{2} + y^{2} + z^{2} = a^{2}, x^{2}-ax + y^{2} leq 0, x geq 0, y geq 0, z geq 0.label{ref8}
$$
Если перейти к сферическим координатам, полагая
$$
x = a cos psi cos varphi, y = a cos psi sin varphi, z =a sin psi,label{ref9}
$$
то система равенств и неравенств eqref{ref8} эквивалентна равенствам eqref{ref9} и неравенствам
$$
0 leq varphi leq psi leq frac{pi}{2},label{ref10}
$$
определяющим в плоскости параметров (varphi, psi) треугольную область (Omega) (рис. 53.2). Интересующая нас простая поверхность есть образ треугольной области (Omega) при отображении eqref{ref9}.
Вычислим коэффициенты первой квадратичной формы. Получаем
$$
boldsymbol{r} = (a cos psi cos varphi, a cos psi sin varphi, a sin psi),nonumber
$$
$$
boldsymbol{r}_{psi} = (-a sin psi cos varphi, -a sin psi sin varphi, a cos psi),nonumber
$$
$$
boldsymbol{r}_{varphi} = (-a cos psi sin varphi, a cos psi cos varphi, 0),nonumber
$$
$$
E = boldsymbol{r}_{psi}^{2} = a^{2}, F = (boldsymbol{r}_{varphi}, boldsymbol{r}_{psi}) = 0, G = boldsymbol{r}_{varphi}^{2} = a^{2} cos^{2} psi.nonumber
$$
Площадь части сферы (x^{2} + y^{2} + z^{2} = a^{2}), вырезаемой из нее цилиндром (x^{2}-ax + y^{2} = 0), равна
$$
S(Sigma) = 4 iintlimits_{Omega} sqrt{EG-F^{2}} dvarphi dpsi = 4 intlimits_{0}^{pi/2} dvarphi intlimits_{varphi}^{pi/2} a^{2} cos psi dpsi = 4a^{2} left(frac{pi}{2}-1right). blacktrianglenonumber
$$
Площадь почти простой поверхности.
Почти простая поверхность задается уравнением (boldsymbol{r} = boldsymbol{r}(u, v)), ((u, v) in overline{Omega}), где (Omega) — плоская область. По определению найдется последовательность ограниченных областей ({Omega_{n}}) такая, что (overline{Omega}_{n} subset Omega_{n + 1}), (displaystyleOmega = bigcup_{n=1}^{infty}Omega_{n}) а поверхности (Sigma_{n}), определяемые уравнениями (boldsymbol{r} = boldsymbol{r}(u, v)), ((u, v) in overline{Omega}), являются простыми. Предположим дополнительно, что области (Omega_{n}) измеримы по Жордану. Тогда под площадью (S(Sigma)) почти простой поверхности будем понимать (displaystylelim_{n rightarrow infty} S(Sigma_{n})).
Так как числовая последовательность (S(Sigma_{n})) монотонно возрастает, то она всегда имеет конечный или бесконечный предел
$$
S(Sigma) = lim_{n rightarrow infty} S(Sigma_{n}) = lim_{n rightarrow infty} iintlimits_{Omega_{n}} sqrt{EG-F^{2}} du dv = iintlimits_{Omega} sqrt{EG-F^{2}} du dv.label{ref11}
$$
Интеграл в формуле eqref{ref11} нужно понимать как несобственный. Если область (Omega) измерима по Жордану, а функция (sqrt{EG-F^{2}}) ограничена на (Omega), то интеграл в формуле eqref{ref11} будет двойным интегралом Римана.
Пример 2.
Найти площадь части боковой поверхности конуса (z^{2} = x^{2} + y^{2}), (z geq 0), вырезаемой из нее цилиндром (x^{2}-ax + y^{2} = 0).
Решение.
(triangle) Обозначим часть боковой поверхности конуса, вырезаемую из нее цилиндром, через (Sigma). Если перейти к цилиндрическим координатам, то (Sigma) будет почти простой поверхностью, определяемой параметрическими уравнениями
$$
x = r cos varphi, y = r sin varphi, z = r, (r, varphi) in Omega,nonumber
$$
$$
Omega = left{(r, varphi): r leq a cos varphi, -frac{pi}{2} leq varphi leq frac{pi}{2}right}.nonumber
$$
Найдем коэффициенты первой квадратичной формы этой поверхности:
$$
boldsymbol{r} = (r cos varphi, r sin varphi, r), boldsymbol{r}_{varphi} = (-r sin varphi, r cos varphi, 0),nonumber
$$
$$
boldsymbol{r}_{r} = (cos varphi, sin varphi, 1), E = boldsymbol{r}_{varphi}^{2} = r^{2}, F = 0, G = boldsymbol{r}_{r}^{2} = 2,nonumber
$$
$$
sqrt{EG-F^{2}} dr dvarphi = rsqrt{2} dr dvarphi.nonumber
$$
Применяя формулу eqref{ref11}, получаем
$$
S(Sigma) = iintlimits_{Omega} sqrt{2}r dr dvarphi = sqrt{2} intlimits_{-pi/2}^{pi/2} dvarphi intlimits_{0}^{a cos varphi} r dr = frac{pi a^{2} sqrt{2}}{4}. blacktrianglenonumber
$$
Если поверхность (Sigma) не является простой или почти простой, но может быть разрезана на конечное число простых кусков, то ее площадью называют сумму площадей всех простых кусков.
Вычисление площади поверхности
Пример 1
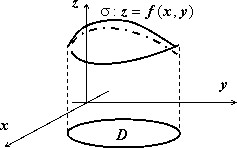
Пусть в пространстве задана кусочно-гладкая поверхность $sigma $, однозначно проектирующаяся в область $mathbf { textit { D } } $ на плоскости $mathbf { textit { Оху } } $. Пусть эта поверхность задаётся уравнением $sigma :;z=f(x,y),;(x,y)in D$. Тогда площадь этой поверхности выражается формулой
$ s(sigma )=iintlimits_D { sqrt { 1+left( { frac { partial f } { partial x } }right)^2+left( { frac { partial f } { partial y } }right)^2 } dxdy } . $
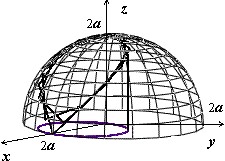
Мы докажем эту формулу позже, когда будем изучать поверхностные интегралы. Сейчас рассмотрим пример: найти площадь лепестков, вырезаемых цилиндром $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } $ = 2$mathbf { textit { ax } } $ из сферы $mathbf { textit { x } } ^ { 2 } +mathbf { textit { y } } ^ { 2 } +mathbf { textit { z } } ^ { 2 } $ = 4$mathbf { textit { a } } ^ { 2 } $ .
Решение:
На рисунке изображён верхний из этих лепестков. Уравнение поверхности $z=sqrt { 4a^2-x^2-y^2 } ,$ вычисляем производные $frac { partial z } { partial x } =-frac { x } { sqrt { 4a^2-x^2-y^2 } } , quad frac { partial z } { partial y } =-frac { y } { sqrt { 4a^2-x^2-y^2 } } ,$ и $s(sigma )=iintlimits_D { sqrt { 1+frac { x^2+y^2 } { 4a^2-x^2-y^2 } dxdy } } =2aiintlimits_D { frac { dxdy } { sqrt { 4a^2-x^2-y^2 } } } $.
Область $mathbf { textit { D } } $ — сдвинутый на $mathbf { textit { а } } $ единиц по оси $mathbf { textit { Ох } } $ круг, поэтому вычисляем в полярных координатах, учитывая симметрию поверхности относительно плоскостей $mathbf { textit { Оху } } $ и $mathbf { textit { Охz } } $:
$s(sigma )=4cdot 2aiintlimits_ { D_ { r,varphi } } { frac { rdrdvarphi } { sqrt { 4a^2-r^2 } } } =8aintlimits_0^ { pi /2 } { dvarphi intlimits_0^ { 2acos varphi } { left( { 4a^2-r^2 }right)^ { -1/2 } rdr } } =-8aintlimits_0^ { pi /2 } { dvarphi left. { left( { 4a^2-r^2 }right)^ { 1/2 } }right|_0^ { 2acos varphi } } = \ =8aintlimits_0^ { pi /2 } { left[ { 2a-2asqrt { 1-cos ^2varphi } }right]dvarphi } =16a^2left. { left( { varphi +cos varphi }right) }right|_0^ { pi /2 } =16a^2left( { pi /2-1 }right)$.
Пример 2
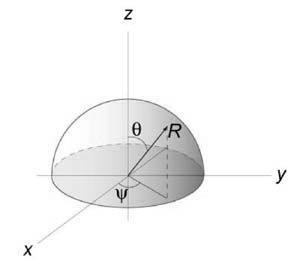
Вычислить площадь cферы радиуса (a.)
Решение:
Рассмотрим верхнюю полусферу. Ее уравнение имеет вид $ { { x^2 } + { y^2 } + { z^2 } = { a^2 } } ;; { text { или } ;;z = sqrt { { a^2 } — { x^2 } — { y^2 } } . } $
Очевидно, область интегрирования (R) представляет собой круг с таким же радиусом (a,) расположенный в центре координат. Площадь полусферы вычисляется по формуле $ { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 + { { left( { frac { { partial z } } { { partial x } } }right) } ^2 } + { { left( { frac { { partial z } } { { partial y } } }right) } ^2 } } dxdy } .$
Найдем частные производные. $ { frac { { partial z } } { { partial x } } } = { frac { partial } { { partial x } } sqrt { { a^2 } — { x^2 } — { y^2 } } } = { frac { { — { 2 } x } } { { { 2 } sqrt { { a^2 } — { x^2 } — { y^2 } } } } } = { — frac { x } { z } , } $ $ { frac { { partial z } } { { partial y } } } = { frac { partial } { { partial y } } sqrt { { a^2 } — { x^2 } — { y^2 } } } = { frac { { — { 2 } y } } { { { 2 } sqrt { { a^2 } — { x^2 } — { y^2 } } } } } = { — frac { y } { z } . } $
Подставляя найденные производные, получаем $ { { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { sqrt { 1 + { { left( { frac { { partial z } } { { partial x } } }right) } ^2 } + { { left( { frac { { partial z } } { { partial y } } }right) } ^2 } } dxdy } } = { iintlimits_R { sqrt { 1 + frac { { { x^2 } } } { { { z^2 } } } + frac { { { y^2 } } } { { { z^2 } } } } dxdy } } = { iintlimits_R { sqrt { frac { { { z^2 } + { x^2 } + { y^2 } } } { { { z^2 } } } } dxdy } } = { iintlimits_R { frac { a } { z } dxdy } . } $
Преобразуем двойной интеграл в полярные координаты. $ { { S_ { largefrac { 1 } { 2 } normalsize } } = iintlimits_R { frac { a } { z } dxdy } } = { intlimits_0^ { 2pi } { intlimits_0^a { frac { a } { { sqrt { { a^2 } — { r^2 } } } } rdrdtheta } } } = { aintlimits_0^ { 2pi } { dtheta } intlimits_0^a { frac { { rdr } } { { sqrt { { a^2 } — { r^2 } } } } } } = { — 2pi aintlimits_0^a { frac { { dleft( { { a^2 } — { r^2 } }right) } } { { 2sqrt { { a^2 } — { r^2 } } } } } } = { — 2pi aleft. { left( { sqrt { { a^2 } — { r^2 } } }right) }right|_ { r = 0 } ^a } = { — 2pi aleft( { 0 — a }right) = 2pi { a^2 } . } $
Площадь поверхности полной сферы, соответственно, равна $S = 2 { S_ { largefrac { 1 } { 2 } normalsize } } = 4pi { a^2 } .$
Определенный интеграл. Площадь криволинейной трапеции
- Теорема о площади криволинейной трапеции
- Формула Ньютона-Лейбница
- Геометрический смысл теоремы Лагранжа о среднем
- Площадь плоской фигуры, ограниченной двумя кривыми
- Примеры
п.1. Теорема о площади криволинейной трапеции
Фигуру, ограниченную прямыми (x=a, x=b), осью абсцисс (y=0) и графиком функции (y=f(x)) называют криволинейной трапецией.
Теорема
Площадь криволинейной трапеции, образованной графиком функции (y=f(x)) на интервале [a;b], равна (F(b)-F(a)), где (F(x)) — первообразная функции (f(x)) на [a;b].
Доказательство:
Выберем на интервале (xin [a;b]). Площадь соответствующей криволинейной трапеции (S(x)) является функцией от (x). Дадим переменной (x) приращение (triangle x).
Площадь криволинейной трапеции на интервале (left[a;x+triangle xright]) равна сумме
(S(x+triangle x)=S(x)+S(triangle x)). Откуда приращение площади: $$ triangle S=S(triangle x)=S(x+triangle x)-S(x) $$ По теореме о среднем (см. ниже в этом параграфе) между (x) и (x+triangle x) всегда найдется такое (t), что приращение площади равно произведению: $$ triangle S=f(t)cdot (x+triangle x-x)=f(t)cdot triangle x $$ Если (triangle xrightarrow 0), то (trightarrow x), и в пределе получаем: begin{gather*} S'(x)=lim_{triangle xrightarrow 0}frac{triangle S}{triangle x}=lim_{triangle xrightarrow 0} frac{f(t)cdot triangle x}{triangle x}=lim_{triangle xrightarrow 0}f(t)=f(x) end{gather*} Т.е. (S(x)) является первообразной для (f(x)) на [a;b]. В общем виде: $$ S(x)=F(x)+C $$ Найдем C. В точке a: $$ S(a)=0=F(a)+CRightarrow C=-F(a) $$ Тогда вся площадь: $$ S=S(b)=F(b)+C=F(b)-F(a) $$ Что и требовалось доказать.
п.2. Формула Ньютона-Лейбница
Площадь криволинейной трапеции, образованной графиком функции (y=f(x)) на интервале [a;b] записывают в виде определенного интеграла: $$ S=int_{a}^{b}f(x)dx $$ По формуле Ньютона-Лейбница определенный интеграл равен: $$ int_{a}^{b}f(x)dx=F(x)|_a^b=F(a)-F(b) $$
Например:
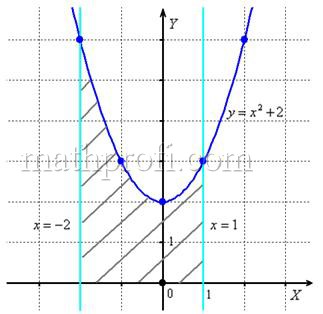
Найдем площадь фигуры, ограниченной осью абсцисс и графиком функции $$ y=3-2x-x^2 $$
 |
Построим график (см. §28 справочника для 8 класса). Это парабола. (alt 0) – ветки вниз. Координаты вершины: begin{gather*} x_0=-frac{b}{2a}=-frac{-2}{2cdot (-1)}=-1,\ y_0=3+2-1=4 end{gather*} Точки пересечения с осью OX: begin{gather*} 3-2x-x^2=0Rightarrow x^2+2x-3=0\ (x+3)(x-1)=0Rightarrow left[ begin{array}{l} x=-3,\ x=1 end{array} right. end{gather*} Точка пересечения с осью OY: $$ x=0, y=3 $$ |
Необходимо найти площадь заштрихованной фигуры.
Функция: (f(x)=3-2x-x^2)
Пределы интегрирования: (a=-3, b=1) begin{gather*} S=int_{-3}^{1}(3-2x-x^2)dx=left(3x-2cdotfrac{x^2}{2}-frac{x^3}{3}right)|_{1}^{-3}=left(3x-x^2-frac{x^3}{3}right)|_{1}^{-3}=\ =left(3-cdot 1-1^2-frac{1^3}{3}right)-left(3cdot(-3)-(-3)^2-frac{(-3)^3}{3}right)=2-frac13+9=10frac23 end{gather*} Ответ: (10frac23)
п.3. Геометрический смысл теоремы Лагранжа о среднем
Теорема Лагранжа о среднем
Если функция (F(x)) непрерывна на отрезке [a;b] и дифференцируема на интервале (a;b), то существует такая точка (muin(a;b)), что $$ F(b)-F(a)=F'(mu)(a-b) $$ Пусть (F'(x)=f(x)), т.е. функция (F(x)) является первообразной для (f(x)). Тогда: $$ F(b)-F(a)=int_{a}^{b}f(x)dx=f(mu)(b-a) $$
Геометрический смысл теоремы Лагранжа о среднем в интегральной форме заключается в том, что площадь криволинейной трапеции равна площади прямоугольника с основанием (d=b-a) и высотой (h=f(mu)), где (aleqmuleq b).
Теорема о среднем используется при доказательстве многих формул, связанных с использованием определенных интегралов (центра тяжести тела, площади поверхности и т.д.).
п.4. Площадь плоской фигуры, ограниченной двумя кривыми
Площадь плоской фигуры, ограниченной прямыми (x=a, x=b, alt b) и кривыми (y=f(x), y=g(x)), причем (f(x)geq g(x)) для любого (xin [a;b]), равна: $$ S=int_{a}^{b}(f(x)-g(x))dx $$
Например:
Найдем площадь фигуры, ограниченной двумя параболами (y=x^2) и (y=4x-x^2).
Найдем точки пересечения парабол: $$ x^2=4x-x^2Rightarrow 2x^2-4x=0Rightarrow 2x(x-2)=0Rightarrow left[ begin{array}{l} x=0\ x=2 end{array} right. $$ Строим графики.
Необходимо найти площадь заштрихованной фигуры.
Функция сверху: (f(x)=4x-x^2)
Функция снизу: (g(x)=x^2)
Пределы интегрирования: (a=0, b=2) begin{gather*} S=int_{0}^{2}left((4x-x^2)-x^2right)dx=int_{0}^{2}(4x-2x^2)dx=left(4cdotfrac{x^2}{2}-2cdotfrac{x^3}{3}right)|_0^2=\ =left(2x^2-frac23 x^3right)|_0^2=2cdot 2^2-frac23cdot 2^3-0=8-frac{16}{3}=frac83=2frac23 end{gather*} Ответ: (2frac23)
п.5. Примеры
Пример 1. Найдите определенный интеграл:
a) (int_{-2}^{3}x^2dx) $$ int_{-2}^{3}x^2dx=frac{x^3}{3}|_{-2}^{3}=frac{3^3}{3}-frac{(-2)^3}{3}=9-frac83=frac{19}{3}=6frac13 $$
б) (int_{0}^{fracpi 3}sinxdx) $$ int_{0}^{fracpi 3}sinxdx=(-cosx)|_{0}^{fracpi 3}=-cosfracpi 3+cos0=-frac12+1=frac12 $$
в) (int_{1}^{2}left(e^x+frac 1xright)dx) $$ int_{1}^{2}left(e^x+frac 1xright)dx=(e^x+ln|x|)|_{1}^{2}=e^2+ln 2-e^1-underbrace{ln 1}_{=0}=e(e-1)+ln 2 $$
г) (int_{2}^{3}(2x-1)^2 dx) begin{gather*} int_{2}^{3}(2x-1)^2 dx=frac12cdotfrac{(2x-3)^3}{3}|_{2}^{3}=frac16((2cdot 3-1)^3)-(2cdot 2-1)^3)=frac{5^3-3^3}{6}=\ =frac{125-27}{6}=frac{98}{6}=frac{49}{3}=16frac13 end{gather*}
д) (int_{1}^{3}frac{dx}{3x-2}) begin{gather*} int_{1}^{3}frac{dx}{3x-2}=frac13cdot ln|3x-2| |_{1}^{3}=frac13left(ln 7-underbrace{ln 1}_{=0}right)=frac{ln 7}{3} end{gather*}
e) (int_{-1}^{4}frac{dx}{sqrt{3x+4}}) begin{gather*} int_{-1}^{4}frac{dx}{sqrt{3x+4}}=frac13cdotfrac{(3x+4)^{-frac12+1}}{-frac12+1}|_{-1}^{4}=frac23sqrt{3x+4}|_{-1}^{4}=\ =frac23left(sqrt{3cdot 4+4}-sqrt{3cdot(-1)+4}right)=frac23(4-1)=2 end{gather*}
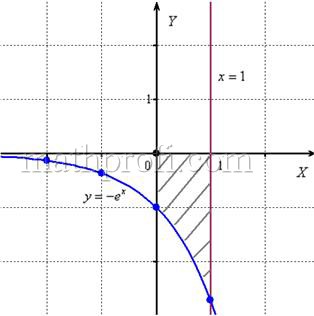
Пример 2. Найдите площадь фигуры под кривой на заданном интервале:
a) (f(x)=x^3+3, xinleft[-1;1right])
б) (f(x)=sin2x, xinleft[0;fracpi 2right])
в) (f(x)=frac4x+3, xinleft[2;6right])
(f(x)=frac4x+3) — гипербола с асимптотами (x=0, y=3)
Площадь под кривой: begin{gather*} S=int_{2}^{6}left(frac4x+3right)dx=(4cdot ln|x|+3x)|_{2}^{6}=(4ln 6+18)-(4ln 2+6)=\ =4(ln 6-ln 2)+12=4lnfrac62+12=4ln 3+12=4(ln 3+3) end{gather*}
г) (f(x)=frac{1}{sqrt{x}}, xinleft[1;4right])
Пример 3. Найдите площадь фигуры, ограниченной линиями:
a) (y=x-2, y=x^2-4x+2)
Найдем точки пересечения прямой и параболы: $$ x-2=x^2-4x+2Rightarrow x^2-5x+4=0Rightarrow (x-1)(x-4)=0Rightarrow left[ begin{array}{l} x=1,\ x=4 end{array} right. $$
Функция сверху: (f(x)=x-2)
Функция снизу: (g(x)=x^2-4x+2)
Пределы интегрирования: (a=1, b=4) begin{gather*} S=int_{1}^{4}left((x-2)-(x^2-4x+2)right)dx=int_{1}^{4}(-x^2+5x-4)dx=\ =left(-frac{x^3}{3}+frac{5x^2}{2}-4xright)|_{1}^{4}=left(-frac{64}{3}+5cdotfrac{16}{2}-4cdot 4right)-left(-frac13+frac52-4right)=\ =-frac{63}{3}+24+1,5=4,5 end{gather*} Ответ: 4,5
б) (y=e^{frac x2}, y=frac1x, x=2, x=3)
Функция сверху: (f(x)=e^{x/2})
Функция снизу: (g(x)=frac1x)
Пределы интегрирования: (a=2, b=3) begin{gather*} S=int_{2}^{3}left(e^{x/2}-frac1xright)dx=(2e^{x/2}-ln|x|)|_{2}^{3}=left(2e^{frac32}-ln 3right)-(2e-ln 2)=\ =2e^{frac32}-2e-ln 3+ln 2=2e(sqrt{e}-1)+lnfrac23 end{gather*} Ответ: (2e(sqrt{e}-1)+lnfrac23)
в*) (y=3-x^2, y=1+|x|)
Найдем точки пересечения ломаной и параболы: begin{gather*} 3-x^2=1+|x|Rightarrow x^2+|x|-2=0Rightarrow left[ begin{array}{l} begin{cases} xgeq 0\ x^2+x-2=0 end{cases} \ begin{cases} xlt 0\ x^2-x-2=0 end{cases} end{array} right. Rightarrow left[ begin{array}{l} begin{cases} xgeq 0\ (x+2)(x-1)=0 end{cases} \ begin{cases} xlt 0\ (x-2)(x+1)=0 end{cases} end{array} right. Rightarrow \ left[ begin{array}{l} begin{cases} xgeq 0\ left[ begin{array}{l} x=-2\ x=1 end{array} right. end{cases} \ begin{cases} xlt 0\ left[ begin{array}{l} x=2\ x=-1 end{array} right. end{cases} end{array} right. Rightarrow left[ begin{array}{l} x=1\ x=-1 end{array} right. end{gather*}
Функция сверху: (f(x)=3-x^2)
Функция снизу: (g(x)=1+|x|)
Пределы интегрирования: (a=-1, b=1)
Чтобы не раскрывать модуль под интегралом, заметим, что площади на интервалах [-1;0] и [0;1] равны, т.к. обе функции четные и симметричные относительно оси OY. Поэтому можно рассматривать только положительные (xinleft[0;1right]), найти для них интеграл (площадь) и умножить на 2: begin{gather*} S=2int_{0}^{1}left((3-x^2)-(1+x)right)dx=2int_{0}^{1}(-x^2-x+2)dx=2left(-frac{x^3}{3}-frac{x^2}{2}+2xright)|_{0}^{1}=\ =2left(-frac13-frac12+2right)-0=frac73=2frac13 end{gather*} Ответ: (2frac13)
г*) (y=3sinx, y=cosx, x=-frac{5pi}{4}, x=fracpi 4)
На отрезке (left[-frac{5pi}{4};-frac{3pi}{4}right]) синус над косинусом, далее на (left[-frac{3pi}{4};frac{pi}{4}right]) — косинус над синусом.
Площадь фигуры, закрашенной голубым, в два раза больше площади фигуры, закрашенной сиреневым. Поэтому общая площадь будет равна трем площадям, закрашенным сиреневым: begin{gather*} S=3int_{-frac{5pi}{4}}^{-frac{3pi}{4}}(sinx-cosx)dx=3(-cosx-sinx)|_{-frac{5pi}{4}}^{-frac{3pi}{4}}=-3(cosx+sinx)|_{-frac{5pi}{4}}^{-frac{3pi}{4}} end{gather*} Прибавим полный период, он одинаков для обеих функций:
(-frac{3pi}{4}+2pi=frac{5pi}{4}; -frac{5pi}{4}+2pi=frac{3pi}{4}) begin{gather*} -3(cosx+sinx)|_{-frac{5pi}{4}}^{-frac{3pi}{4}}=-3left(cosleft(frac{5pi}{4}right)+sinleft(frac{5pi}{4}right)-cosleft(frac{3pi}{4}right)-sinleft(frac{3pi}{4}right)right)=\ =-3left(-frac{sqrt{2}}{2}-frac{sqrt{2}}{2}+frac{sqrt{2}}{2}-frac{sqrt{2}}{2}right)=3sqrt{2} end{gather*} Ответ: (3sqrt{2})
Пример 4*. Пусть (S(k)) — это площадь фигуры, образованной параболой (y=x^2+2x-3) и прямой (y=kx+1). Найдите (S(-1)) и вычислите наименьшее значение (S(k)).
1) Найдем (S(-1)).
(k=-1, y=-x+1 )
 |
Точки пересечения прямой и параболы: begin{gather*} -x+1=x^2+2x-3\ x^2+3x-4=0\ (x+4)(x-1)=0Rightarrow left[ begin{array}{l} x=-4,\ x=1 end{array} right. end{gather*} Функция сверху: (y=-x+1) Функция снизу: (y=x^2+2x-3) Пределы интегрирования: (a=-4, b=1) |
begin{gather*} S(-1)=int_{-4}^{1}left((-x+1)-(x^2+2x-3)right)dx=int_{-4}^{1}(-x-3x+4)dx=\ =left(-frac{x^3}{3}-frac{3x^2}{2}+4xright)|_{-4}^{1}=left(-frac13-frac32+4right)-left(frac{64}{3}-24-16right)=-21frac23+42frac12=20frac56 end{gather*}
2) Решаем в общем виде.
Все прямые (y=kx+1) проходят через точку (0;1) и при образовании фигуры находятся над параболой.
Точки пересечения прямой и параболы: begin{gather*} kx+1=x^2+2x-3Rightarrow x^2+(2-k)x-4=0\ D=(2-k)^2-4cdot (-4)=(k-2)^2+16gt 0 end{gather*} Дискриминант (Dgt 0) при всех (k). Точки пересечения (пределы интегрирования): $$ x_{1,2}=frac{-(2-k)pmsqrt{D}}{2}=frac{k-2pmsqrt{D}}{2} $$ Разность корней: $$ x_2-x_1=sqrt{D}=sqrt{(k-2)^2+16} $$ Минимальное значение разности корней будет при (k=2).
Площадь: begin{gather*} S(k)=int_{x_1}^{x_2}left((kx+1)-(x^2+2x-3)right)dx=int_{x_1}^{x_2}(-x^2+(k-2)x+4)dx=\ =left(-frac{x^3}{3}+frac{(k-2)x^2}{2}+4xright)|_{x_1}^{x_2}=-frac13(x_2^3-x_1^3)+frac{k-2}{2}(x_2^2-x_1^2)+4(x_2-x_1) end{gather*}
 |
begin{gather*} S(k)_{min}=S(2)\ x_{1,2}=pm 2\ S(2)=-frac13cdot(2^3+2^3)+0+4sqrt{16}=\ =-frac{16}{3}+16=frac{32}{3}=10frac23 end{gather*} |
Ответ: 1) (S(-1)=20frac56); 2) (S(k)_{min}=S(2)=10frac23)
Пример 5*. Фигура ограничена линиями (y=(x+3)^2, y=0, x=0). Под каким углом к оси OX надо провести прямые через точку (0;9), чтобы они разбивали фигуру на три равновеликие части?
 |
Площадь криволинейной трапеции AOB: begin{gather*} S_0=int_{-3}^{0}(x+3)^2dx=frac{(x+3)^3}{3}|_{-3}^{0}=\ =9-0=9 end{gather*} Площадь каждой части: (S_i=frac13 S_0=3) Точки (C(x_1; 0)) и (D(x_2; 0)) c (-3lt x_1lt x_2lt 0) такие, что прямые AC и AD отсекают по 1/3 от фигуры. Площадь прямоугольного треугольника (triangle AOD): begin{gather*} S_3=frac12|x_2|cdot 9=3Rightarrow |x_2|=frac69=frac23Rightarrow\ x_2=-frac23 end{gather*} Площадь прямоугольного треугольника (triangle AOC): begin{gather*} S_2+S_3=frac12|x_1|cdot 9=6Rightarrow |x_1|=frac{12}{9}=frac43Rightarrow\ x_1=-frac43 end{gather*} |
Находим углы соответствующих прямых.
Для (x_1: tgalpha=frac{9}{|x_1|}=frac{9}{4/3}=frac{27}{4}, alpha=arctgfrac{27}{4})
Для (x_x: tgbeta=frac{9}{|x_2|}=frac{9}{2/3}=frac{27}{2}, beta=arctgfrac{27}{2})
Ответ: (arctgfrac{27}{4}) и (arctgfrac{27}{2})
Калькулятор онлайн.
Вычислить определенный интеграл (площадь криволинейной трапеции).
Этот математический калькулятор онлайн поможет вам вычислить определенный интеграл (площадь криволинейной трапеции).
Программа для вычисления определенного интеграла (площади криволинейной трапеции) не просто даёт ответ задачи, она приводит подробное
решение с пояснениями, т.е. отображает процесс интегрирования функции.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Вы можете посмотреть теорию о определенном интеграле.
Примеры подробного решения >>
Введите подинтегральную функцию и пределы интегрирования
Наши игры, головоломки, эмуляторы:
Немного теории.
Определенный интеграл.
Задачи, приводящие к понятию определенного интеграла
Задача 1 (о вычислении площади криволинейной трапеции).

В декартовой прямоугольной системе координат xOy дана фигура (см. рисунок), ограниченная осью х, прямыми х = a, х = b (a < b)
и графиком непрерывной и неотрицательной на отрезке [а; b] функции y = f(x); назовем эту фигуру криволинейной трапецией. Требуется
вычислить площадь криволинейной трапеции.
Решение. Геометрия дает нам рецепты для вычисления площадей многоугольников и некоторых частей круга (сектора, сегмента). Используя
геометрические соображения, мы сумеем найти лишь приближенное значение искомой площади, рассуждая следующим образом.
Разобьем отрезок [а; b] (основание криволинейной трапеции) на n равных частей; это разбиение осуществим с помощью точек x1,
x2, … xk, … xn-1. Проведем через эти точки прямые, параллельные оси у. Тогда заданная
криволинейная трапеция разобьется на n частей, на n узеньких столбиков. Площадь всей трапеции равна сумме площадей столбиков.
Рассмотрим отдельно k-ый столбик, т.е. криволинейную трапецию, основанием которой служит отрезок [xk; xk+1].
Заменим его прямоугольником с тем же основанием и высотой, равной f(xk) (см. рисунок). Площадь прямоугольника равна
( f(x_k) cdot Delta x_k ), где ( Delta x_k ) — длина отрезка [xk; xk+1]; естественно
считать составленное произведение приближенным значением площади k-го столбика.
Если теперь сделать то же самое со всеми остальными столбиками, то придем к следующему результату: площадь S заданной криволинейной
трапеции приближенно равна площади Sn ступенчатой фигуры, составленной из n прямоугольников (см. рисунок):
( S_n = f(x_0)Delta x_0 + dots + f(x_k)Delta x_k + dots + f(x_{n-1})Delta x_{n-1} )
Здесь ради единообразия обозначений мы считаем, что a = х0, b = xn;
( Delta x_0 ) — длина отрезка [x0; x1],
( Delta x_1 ) — длина отрезка [x1; x2], и т.д;
при этом, как мы условились выше, ( Delta x_0 = dots = Delta x_{n-1} )
Итак, ( S approx S_n ), причем это приближенное равенство тем точнее, чем больше n.
По определению полагают, что искомая площадь криволинейной трапеции равна пределу последовательности (Sn):
$$ S = lim_{n to infty} S_n $$
Задача 2 (о перемещении точки)
По прямой движется материальная точка. Зависимость скорости от времени выражается формулой v = v(t). Найти перемещение точки
за промежуток времени [а; b].
Решение. Если бы движение было равномерным, то задача решалась бы очень просто: s = vt, т.е. s = v(b-а). Для неравномерного движения
приходится использовать те же идеи, на которых было основано решение предыдущей задачи.
1) Разделим промежуток времени [а; b] на n равных частей.
2) Рассмотрим промежуток времени [tk; tk+1] и будем считать, что в этот промежуток времени скорость была
постоянной, такой, как в момент времени tk. Итак, мы считаем, что v = v(tk).
3) Найдем приближенное значение перемещения точки за промежуток времени [tk; tk+1], это приближенное
значение обозначим sk
( s_k = v(t_k) Delta t_k )
4) Найдем приближенное значение перемещения s:
( s approx S_n ) где
( S_n = s_0 + dots + s_{n-1} = v(t_0)Delta t_0 + dots + v(t_{n-1}) Delta t_{n-1} )
5) Искомое перемещение равно пределу последовательности (Sn):
$$ s = lim_{n to infty} S_n $$
Подведем итоги. Решения различных задач свелись к одной и той же математической модели. Многие задачи из различных областей
науки и техники приводят в процессе решения к такой же модели. Значит, данную математическую модель надо специально изучить.
Понятие определенного интеграла
Дадим математическое описание той модели, которая была построена в трех рассмотренных задачах для функции y = f(x),
непрерывной (но необязательно неотрицательной, как это предполагалось в рассмотренных задачах) на отрезке [а; b]:
1) разбиваем отрезок [а; b] на n равных частей;
2) составляем сумму $$ S_n = f(x_0)Delta x_0 + f(x_1)Delta x_1 + dots + f(x_{n-1})Delta x_{n-1} $$
3) вычисляем $$ lim_{n to infty} S_n $$
В курсе математического анализа доказано, что этот предел в случае непрерывной (или кусочно-непрерывной) функции существует.
Его называют определенным интегралом от функции y = f(x) по отрезку [а; b] и обозначают так:
( intlimits_a^b f(x) dx )
Числа a и b называют пределами интегрирования (соответственно нижним и верхним).
Вернемся к рассмотренным выше задачам. Определение площади, данное в задаче 1, теперь можно переписать следующим образом:
( S = intlimits_a^b f(x) dx )
здесь S — площадь криволинейной трапеции, изображенной на рисунке выше. В этом состоит геометрический смысл определенного интеграла.
Определение перемещения s точки, движущейся по прямой со скоростью v = v(t), за промежуток времени от t = a до t = b, данное
в задаче 2, можно переписать так:
( S = intlimits_a^b v(t) dt )
Формула Ньютона — Лейбница
Для начала ответим на вопрос: какая связь между определенным интегралом и первообразной?
Ответ можно найти в задаче 2. С одной стороны, перемещение s точки, движущейся по прямой со скоростью v = v(t), за промежуток
времени от t = а до t = b и вычисляется по формуле
( S = intlimits_a^b v(t) dt )
С другой стороны, координата движущейся точки есть первообразная для скорости — обозначим ее s(t); значит, перемещение s
выражается формулой s = s(b) — s(a). В итоге получаем:
( S = intlimits_a^b v(t) dt = s(b)-s(a) )
где s(t) — первообразная для v(t).
В курсе математического анализа доказана следующая теорема.
Теорема. Если функция y = f(x) непрерывна на отрезке [а; b], то справедлива формула
( S = intlimits_a^b f(x) dx = F(b)-F(a) )
где F(x) — первообразная для f(x).
Приведенную формулу обычно называют формулой Ньютона — Лейбница в честь английского физика Исаака Ньютона (1643—1727)
и немецкого философа Готфрида Лейбница (1646— 1716), получивших ее независимо друг от друга и практически одновременно.
На практике вместо записи F(b) — F(a) используют запись ( left. F(x)right|_a^b )
(ее называют иногда двойной подстановкой) и, соответственно, переписывают формулу Ньютона — Лейбница в таком виде:
( S = intlimits_a^b f(x) dx = left. F(x)right|_a^b )
Вычисляя определенный интеграл, сначала находят первообразную, а затем осуществляют двойную подстановку.
Опираясь на формулу Ньютона — Лейбница, можно получить два свойства определенного интеграла.
Свойство 1. Интеграл от суммы функций равен сумме интегралов:
( intlimits_a^b (f(x) + g(x))dx = intlimits_a^b f(x)dx + intlimits_a^b g(x)dx )
Свойство 2. Постоянный множитель можно вынести за знак интеграла:
( intlimits_a^b kf(x)dx = k intlimits_a^b f(x)dx )
Вычисление площадей плоских фигур с помощью определенного интеграла
С помощью интеграла можно вычислять площади не только криволинейных трапеций, но и плоских
фигур более сложного вида, например такого, который представлен на рисунке. Фигура Р ограничена прямыми х = а, х = b и графиками
непрерывных функций y = f(x), y = g(x), причем на отрезке [а; b] выполняется неравенство ( g(x) leqslant f(x) ). Чтобы вычислить
площадь S такой фигуры, будем действовать следующим образом:
( S = S_{ABCD} = S_{aDCb} — S_{aABb} = intlimits_a^b f(x) dx — intlimits_a^b g(x) dx = )
( = intlimits_a^b (f(x)-g(x))dx )
Итак, площадь S фигуры, ограниченной прямыми х = а, х = b и графиками функций y = f(x), y = g(x), непрерывных на отрезке [a; b]
и таких, что для любого x из отрезка [а; b] выполняется неравенство ( g(x) leqslant f(x) ), вычисляется по формуле
( S = intlimits_a^b (f(x)-g(x))dx )
Таблица неопределённых интегралов (первообразных) некоторых функций
$$ int 0 cdot dx = C $$
$$ int 1 cdot dx = x+C $$
$$ int x^n dx = frac{x^{n+1}}{n+1} +C ;; (n neq -1) $$
$$ int frac{1}{x} dx = ln |x| +C $$
$$ int e^x dx = e^x +C $$
$$ int a^x dx = frac{a^x}{ln a} +C ;; (a>0, ;; a neq 1) $$
$$ int cos x dx = sin x +C $$
$$ int sin x dx = -cos x +C $$
$$ int frac{dx}{cos^2 x} = text{tg} x +C $$
$$ int frac{dx}{sin^2 x} = -text{ctg} x +C $$
$$ int frac{dx}{sqrt{1-x^2}} = text{arcsin} x +C $$
$$ int frac{dx}{1+x^2} = text{arctg} x +C $$
$$ int text{ch} x dx = text{sh} x +C $$
$$ int text{sh} x dx = text{ch} x +C $$
Задачка это школьная, но, несмотря на то, почти 100% встретится в вашем курсе высшей математики. Поэтому со всей серьёзностью отнесёмся ко ВСЕМ примерам, и первое, что нужно сделать – это ознакомиться с Приложением Графики функций, чтобы освежить в памяти технику построения элементарных графиков. …Есть? Отлично! Типовая формулировка задания звучит так:
Пример 10
Вычислить площадь фигуры, ограниченной линиями .
И первый важнейший этап решения состоит как раз в построении чертежа. При этом я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций.
В нашей задаче: прямая определяет ось
, прямые
параллельны оси
и парабола
симметрична относительно оси
, для неё находим несколько опорных точек:
Искомую фигуру желательно штриховать:
Второй этап состоит в том, чтобы правильно составить и правильно вычислить определённый интеграл. На отрезке график функции
расположен над осью
, поэтому искомая площадь:
Ответ:
После того, как задание выполнено, полезно взглянуть на чертёж
и прикинуть, реалистичный ли получился ответ.
И мы «на глазок» подсчитываем количество заштрихованных клеточек – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получилось, скажем, 20 квадратных единиц, то, очевидно, где-то допущена ошибка – в построенную фигуру 20 клеток явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.
Пример 11
Вычислить площадь фигуры, ограниченной линиями и осью
Быстренько разминаемся (обязательно!) и рассматриваем «зеркальную» ситуацию – когда криволинейная трапеция расположена под осью :
Пример 12
Вычислить площадь фигуры, ограниченной линиями ,
и координатными осями.
Решение: найдём несколько опорных точек для построения экспоненты:
и выполним чертёж, получая фигуру площадью около двух клеток:
Если криволинейная трапеция расположена не выше оси , то её площадь можно найти по формуле:
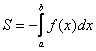
В данном случае:
Ответ: – ну что же, очень и очень похоже на правду.
На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому от простейших школьных задачек мы переходим к более содержательным примерам:
Пример 13
Найти площадь плоской фигуры, ограниченной линиями ,
.
Решение: сначала нужно выполнить чертеж, при этом нас особо интересуют точки пересечения параболы и прямой
, поскольку здесь будут находиться пределы интегрирования. Найти их можно двумя способами. Первый способ – аналитический. Составим и решим уравнение:
таким образом:
Достоинство аналитического способа состоит в его точности, а недостаток – в длительности (и в этом примере нам ещё повезло). Поэтому во многих задачах бывает выгоднее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой».
С прямой всё понятно, а вот для построения параболы удобно найти её вершину, для этого возьмём производную и приравняем её к нулю:
– именно в этой точке и будет находиться вершина. И, в силу симметрии параболы, остальные опорные точки найдём по принципу «влево-вправо»:
Выполним чертеж:
А теперь рабочая формула: если на отрезке некоторая непрерывная функция
больше либо равна непрерывной функции
, то площадь фигуры, ограниченной графиками этих функций и отрезками прямых
, можно найти по формуле:
Здесь уже не надо думать, где расположена фигура – над осью или под осью, а, грубо говоря, важно, какой из двух графиков ВЫШЕ.
В нашем примере очевидно, что на отрезке парабола располагается выше прямой, а поэтому из
нужно вычесть
Завершение решения может выглядеть так:
На отрезке :
, по соответствующей формуле:
Ответ:
Следует отметить, что простые формулы, рассмотренные в начале параграфа – это частные случаи формулы 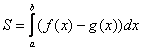
задаётся уравнением
, то одна из функций будет нулевой, и в зависимости от того, выше или ниже лежит криволинейная трапеция, мы получим формулу
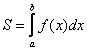
А сейчас пара типовых задач для самостоятельного решения
Пример 14
Найти площадь фигур, ограниченных линиями:
а) ,
.
б) ,
,
Решение с чертежами и краткими комментариями в конце книги
В ходе решения рассматриваемой задачи иногда случается забавный казус. Чертеж выполнен правильно, интеграл решён правильно, но по невнимательности… найдена площадь не той фигуры, именно так несколько раз ошибался ваш покорный слуга. Вот реальный случай из жизни:
Пример 15
Вычислить площадь фигуры, ограниченной линиями
Решение: выполним бесхитростный чертёж,
хитрость которого состоит в том, что искомая площадь заштрихована зелёным цветом (внимательно смотрИте на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована серым цветом! Особое коварство состоит в том, что прямую можно недочертить до оси
, и тогда мы вовсе не увидим нужную фигуру.
Этот пример ещё и полезен тем, что в нём площадь фигуры считается с помощью двух определённых интегралов. Действительно:
1) на отрезке над осью
расположен график прямой
;
2) на отрезке над осью
расположен график гиперболы
.
Совершенно понятно, что площади можно (и нужно) сложить:
Ответ:
И познавательный пример для самостоятельного решения:
Пример 16
Вычислить площадь фигуры, ограниченной линиями ,
,
и координатными осями.
Итак, систематизируем важные моменты этой задачи:
На первом шаге ВНИМАТЕЛЬНО изучаем условие – КАКИЕ функции нам даны? Ошибки бывают даже здесь, в частности, арккотангенс зачастую принимают за арктангенс. Это, кстати, относится и к другим заданием, где встречается арккотангенс.
Далее следует ПРАВИЛЬНО выполнить чертёж. Сначала лучше построить прямые (если они есть), затем графики других функций (если они есть J). Последние во многих случаях выгоднее строить поточечно – найти несколько опорных точек и аккуратно соединить их линией.
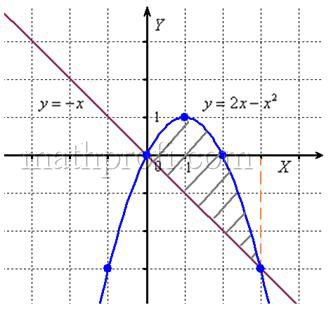
Но здесь могут подстерегать следующие трудности. Во-первых, из чертежа не всегда понятны пределы интегрирования – так бывает, когда они дробные. На mathprofi.ru в соответствующей статье я рассмотрел пример с параболой и прямой
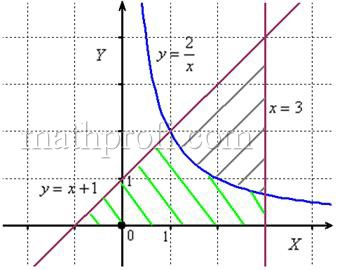
, где из чертежа не понятна одна из точек их пересечения. В таких случаях следует использовать аналитический метод, составляем уравнение:
и находим его корни:
– нижний предел интегрирования,
– верхний предел.
Во-вторых, не всегда понятен «внешний вид» линии, и функция (Пример 16) – яркий тому пример. Я и сам «с ходу» не представляю, как выглядит график этой функции. Здесь можно воспользоваться специализированными программами или онлайн сервисами (а-ля «построить график онлайн»), а в экстремальной ситуации найти побольше опорных точек (штук 10-15), чтобы поточнее провести «неизвестную» кривую.
Ну и, конечно, я призываю вас повышать свои знания и навыки в графиках, в частности, приведу прямую ссылку на особо полезную статью:
http://mathprofi.ru/kak_postroit_grafik_funkcii_s_pomoshyu_preobrazovanii.html
После того, как чертёж построен, анализируем полученную фигуру – ещё раз окидываем взглядом предложенные функции и перепроверяем, ТА ЛИ это фигура. Затем анализируем её форму и расположение, бывает, что площадь достаточно сложнА и тогда её следует разделить на две, а то и на три части.
Составляем определённый интеграл или несколько интегралов по формуле 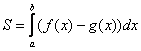
Решаем определённый интеграл (ы). При этом он может оказаться достаточно сложным, и тогда применяем поэтапный алгоритм: 1) находим первообразную и проверяем её дифференцированием, 2) используем формулу Ньютона-Лейбница.
Результат полезно проверить с помощью программного обеспечения / онлайн сервисов или просто «прикинуть» по чертежу по клеточкам. Но и то, и другое не всегда осуществимо, поэтому крайне внимательно относимся к каждому этапу решения!


| Оглавление |
Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин