Как найти площадь круга через радиус формула

Определение окружности

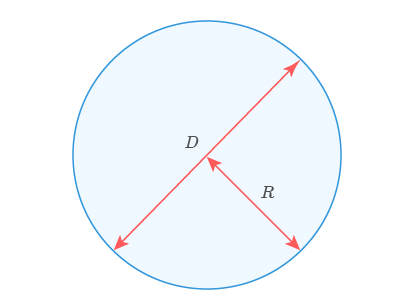
Окружность – это замкнутая линия, причем расстояние от любой точки, находящейся на этой линии, до центра окружности одинаково. Кругом является внутренняя часть окружности.

Онлайн-калькулятор площади круга

Площадь круга.png

Тот самый отрезок, который соединяет выбранную точку на окружности с ее центром, называется радиусом RR.
Длина радиуса, взятая в двойном размере, называется диаметром окружности DD.

То есть D=2RD=2R.

Как найти площадь круга

Площадь круга можно найти двумя способами:

  • используя радиус круга,
  • используя диаметр круга.

Остановимся чуть подробнее на каждом способе и рассмотрим несколько примеров.

Формула площади круга через радиус круга

Сначала разберем общий случай.

Пусть нам дана окружность OO произвольного радиуса R.R. Площадь круга через радиус вычисляется при помощи формулы

S=πR2S=pi R^2,

где πpi – число «Пи», выражающее отношение длины окружности к ее диаметру и численно равное около 3,143,14,

RR – радиус нашей окружности.

Теперь, чтобы было более понятно, рассмотрим пару практических примеров.

Пример

Найдите площадь круга, радиус которого равен 6 см.
Ответ дайте, округленный до целого числа.

Решение:

Пользуемся нашей формулой для вычисления площади круга и получаем:

S=πR2=3,14⋅6⋅6=3,14⋅36=113.S=pi R^2=3,14cdot 6 cdot 6=3,14 cdot 36=113.

Ответ: 113 см2.

Формула площади круга через диаметр

Рассмотрим сначала обобщенный случай без использования цифр.

Формула вычисления площади круга с помощью диаметра немного отличается от формулы, в которой мы использовали радиус. Но ответ остается, безусловно, таким же.

Итак, наша формула выглядит следующим образом:

S=πD24S=pi frac{D^2}{4}

Давайте разберемся, откуда она вообще взялась.

Для начала выразим радиус через диаметр. Получаем R=D2R=frac{D}{2}, затем подставляем полученное выражение в нашу исходную формулу S=πR2S=pi R^2 и получаем результат: S=πD222S=pi frac{D^2}{2^2}, далее упрощаем и выходим на окончательный ответ S=πD24S=pi frac{D^2}{4}.

Пример

Найти площадь круга, если известно, что четвертая часть диаметра равна 2,5 см.

Решение:

Находим диаметр:

D4=2,5.frac{D}{4} =2,5.

Отсюда,

D=2,5⋅4=10.D=2,5 cdot 4=10.

Подставляем значения в формулу:

S=πD24=3,14⋅1024=3,14⋅1004=3,14⋅25=78,5S=pi frac{D^2}{4} =3,14 cdot frac{10^2}{4} =3,14 cdot frac{100}{4} =3,14 cdot 25=78,5

Ответ: 78,5 см2.

Пример решения задачи посложнее.

Пример

Имеется два круга. Площадь первого 153,86153,86 см2. Найдите площадь второго круга, радиус которого в 22 раза больше радиуса первого круга.

Решение:
Для решения задачи нам в первую очередь нужно найти радиус первого круга. Из формулы S=πR2S=pi R^2 находим, что R=SπR=sqrt{frac{S}{pi}}.

R=153.863.14=49=7.R=sqrt{frac{153.86}{3.14}}=sqrt{49} = 7.

Радиус второго круга равен 7⋅2=14.7 cdot 2=14.

Наконец, найдем площадь этого круга: S=πR2=3.14⋅142=3,14⋅196=615,44.S=pi R^2=3.14cdot14^2=3,14 cdot 196=615,44.

Ответ: 615,44615,44 см2.

Ищете специалиста, который сможет написать контрольную работу на заказ для вас? Наши эксперты подбирают индивидуальный подход к каждому клиенту!

Тест по теме “Площадь круга”

Источник

Как рассчитать площадь круга

На данной странице калькулятор поможет рассчитать площадь круга онлайн. Для расчета задайте радиус, диаметр или длину окружности.

Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круг) на расстояние, не превышающее заданное (радиус круга).

Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.

Через радиус

Площадь круга через радиус

Формула для нахождения площади круга через радиус:

π — константа равная (3.14); r — радиус круга.

Через диаметр

Площадь круга через диаметр

Формула для нахождения площади круга через диаметр:

π — константа равная (3.14); d — диаметр.

Через длину окружности

Площадь круга через длину окружности

Формула для нахождения площади круга через длину окружности:

π — константа равная (3.14); l — длина окружности.

Источник

Площадь круга через Диаметр

S — площадь круга,

d — диаметр круга,

π ≈ 3,141592653589

Площадь круга через Радиус

S — площадь круга,

r — радиус круга,

π ≈ 3,141592653589

Площадь круга через Длину Окружности

S — площадь круга,

l — длина окружности,

π ≈ 3,141592653589

Определения и термины

Круг — множество точек плоскости, расстояние до которых от данной точки (центра круга) не превышает заданного расстояния (радиуса круга).

Радиус круга — отрезок, соединяющий центр круга с любой точкой, которая лежит на внешней окружности круг

Диаметр круга — отрезок, соединяющий любые две точки, лежащие на внешней окружности круга, и проходящий через центр круга

Окружность — замкнутая плоская кривая состоящия из всех точек полскости равноудаленных от заданной точки (центра окружности)

Число Пи (π) — математическая константа, которая выражает отношение длины окружности к её диаметру.
Равно приблизительно 3,141592653589…

Площадь окружности

Окружность, по своей сути, является границей круга — замкнутой плоской кривой. Из определения следует, что площади окружности не существует,
а существует Площадь круга.

Источник


Загрузить PDF


Загрузить PDF

Некоторые учащиеся не понимают, как найти площадь круга по исходным данным. Для начала нужно запомнить формулу, по которой вычисляется площадь круга: S=pi r^{2}. Формула проста: чтобы найти площадь круга, нужно знать только его радиус. Но нужно уметь преобразовывать другие исходные величины, чтобы воспользоваться этой формулой.

  1. Изображение с названием Calculate the Area of a Circle Step 1

    1

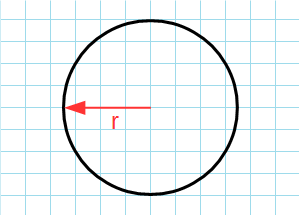
    Найдите радиус круга. Радиус – это отрезок, соединяющий центр круга с любой точкой внешней окружности круга. Радиус можно измерить в любом направлении: он будет одним и тем же. Радиус также равен половине диаметра круга. Диаметр – это отрезок, который проходит через центр круга и соединяет две точки внешней окружности круга.[1]

    • Как правило, значение радиуса дано в условиях задачи. Довольно трудно найти точный центр круга, если только он не обозначен на круге, который нарисован на бумаге.
    • Например, радиус круга равен 6 см.

  2. Изображение с названием Calculate the Area of a Circle Step 2

    2

    Возведите радиус в квадрат. Формула для вычисления площади круга: S=pi r^{2}, где r – радиус, который возведен во вторую степень (в квадрат).[2]

  3. Изображение с названием Calculate the Area of a Circle Step 3

    3

    Полученный результат умножьте на число Пи. Это число обозначается греческой буквой pi и представляет собой математическую константу, которая характеризует взаимосвязь радиуса и площади круга. Число Пи приблизительно равно 3,14. Точное значение числа Пи включает бесконечное количество цифр. Иногда ответ (площадь круга) записывается с постоянной pi .[3]

    • В нашем примере (r = 6 см) площадь вычисляется так:

  4. Изображение с названием Calculate the Area of a Circle Step 4

    4

    Запишите ответ. Помните, что площадь измеряется в квадратных единицах. Если радиус дан в сантиметрах, площадь измеряется в квадратных сантиметрах. Если радиус дан в миллиметрах, площадь измеряется в квадратных миллиметрах. Уточните у преподавателя, нужно ли представить ответ с постоянной pi или в числовой форме, используя приблизительное значение числа Пи. Если требование не ясно, запишите оба варианта ответа.[4]

    • В нашем примере (r = 6 см) S = 36pi см2 или S = 113,04 см2.

    Реклама

  1. Изображение с названием Calculate the Area of a Circle Step 5

    1

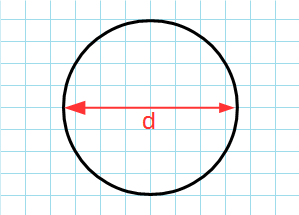
    Измерьте или запишите диаметр. В некоторых задачах радиус не дан. Вместо радиуса указывается диаметр. Если диаметр нарисован на бумаге, измерьте его с помощью линейки. Скорее всего, числовое значение диаметра будет задано.

    • Например, диаметр круга равен 20 мм.

  2. Изображение с названием Calculate the Area of a Circle Step 6

    2

    Разделите диаметр пополам. Помните, что диаметр равен удвоенному радиусу. Поэтому разделите любое значение диаметра на 2, чтобы найти радиус.

    • Таким образом, если диаметр круга равен 20 мм, то радиус круга равен 20/2 = 10 мм.

  3. Изображение с названием Calculate the Area of a Circle Step 7

    3

    Воспользуйтесь стандартной формулой для вычисления площади круга. Найдя радиус, воспользуйтесь формулой S=pi r^{2}, чтобы вычислить площадь круга. Подставьте значение радиуса и выполните вычисления следующим образом:

  4. Изображение с названием Calculate the Area of a Circle Step 8

    4

    Запишите ответ. Помните, что площадь измеряется в квадратных единицах. В нашем примере диаметр дан в миллиметрах, поэтому радиус тоже измеряется в миллиметрах, а площадь в квадратных миллиметрах. В нашем примере S = 100pi мм2.

    • Также ответ можно представить в численной форме, используя вместо pi приблизительное значение 3,14. В этом случае S = (100)(3,14) = 314 мм2.

    Реклама

  1. Изображение с названием Calculate the Area of a Circle Step 9

    1

    Запишите преобразованную формулу. Если известна длина окружности круга, можно воспользоваться преобразованной формулой для вычисления его площади. Такая формула включает длину окружности, а не радиус, и записывается так:

    • S={frac {C^{2}}{4pi }}

  2. Изображение с названием Calculate the Area of a Circle Step 10

    2

    Измерьте или запишите длину окружности. В некоторых ситуациях нельзя точно измерить диаметр или радиус. Если диаметр не нарисован или центр не отмечен, очень сложно найти точный центр круга. Длину окружности некоторых предметов (например, сковороды) довольно легко измерить с помощью рулетки, то есть можно найти более точное значение длины окружности, чем диаметра.[5]

    • Например, длина окружности круга (или круглого предмета) равна 42 см.

  3. Изображение с названием Calculate the Area of a Circle Step 11

    3

  4. Изображение с названием Calculate the Area of a Circle Step 12

    4

    Запишите формулу для вычисления площади круга. Запишите преобразованную формулу на основе соотношения между длиной окружности и радиусом. Подставьте последнее равенство в стандартную формулу для вычисления площади круга:[7]

  5. Изображение с названием Calculate the Area of a Circle Step 13

    5

    Воспользуйтесь преобразованной формулой, чтобы решить задачу. Теперь в формуле вместо радиуса присутствует длина окружности, поэтому можно вычислить площадь круга по известной длине окружности. Подставьте значение длины окружности и выполните вычисления следующим образом:[8]

  6. Изображение с названием Calculate the Area of a Circle Step 14

    6

    Запишите ответ. Если длина окружности дана в виде числа, а не произведения числа и pi , ответ можно записать с pi в знаменателе. Или вместо числа Пи подставьте его приблизительное значение (3,14).[9]

    Реклама

  1. Изображение с названием Calculate the Area of a Circle Step 15

    1

    Запишите известные величины. В некоторых задачах дана площадь сектора круга, по которой нужно найти площадь всего круга. Внимательно прочитайте такую задачу; ее условие может выглядеть так: «Площадь сектора круга равна 15pi см2. Найдите площадь всего круга».[10]

  2. Изображение с названием Calculate the Area of a Circle Step 16

    2

    Запомните определение сектора. Сектор круга – это часть круга, которая ограничена дугой и двумя радиусами. Пространство между такими радиусами и дугой называется сектором.[11]

  3. Изображение с названием Calculate the Area of a Circle Step 17

    3

    Измерьте центральный угол сектора. Воспользуйтесь транспортиром, чтобы измерить угол между двумя радиусами. Линейку (прямолинейную шкалу) совместите с одним из радиусов, причем центр линейки должен совпадать с центром круга. Затем найдите величину угла; для этого посмотрите на точку пересечения второго радиуса с угломерной шкалой.[12]

    • Не перепутайте внутренний и внешний угол между двумя радиусами. В задаче должно быть указано, с каким углом работать. Помните, что сумма внутреннего и внешнего углов равна 360 градусов.
    • Во многих задачах центральный угол дан, то есть измерять его не нужно. Например, в задаче может быть сказано: «Центральный угол сектора равен 45 градусов»; если это не так, измерьте центральный угол.

  4. Изображение с названием Calculate the Area of a Circle Step 18

    4

    Используйте преобразованную формулу для вычисления площади круга. Если известны площадь сектора и его центральный угол, используйте следующую преобразованную формулу, чтобы найти площадь круга: [13]

    • S_{{kr}}=S_{{sek}}{frac {360}{C}}

  5. Изображение с названием Calculate the Area of a Circle Step 19

    5

    Подставьте известные значения и найдите площадь круга. В нашем примере известно, что центральный угол равен 45 градусов, а площадь сектора равна 15pi . Подставьте эти значения в формулу:[14]

  6. Изображение с названием Calculate the Area of a Circle Step 20

    6

    Запишите ответ. В нашем примере сектор составлял одну восьмую полного круга. Поэтому площадь полного круга равна 120pi см2. Так как площадь сектора дана с постоянной pi , скорее всего, ответ тоже можно представить с этой постоянной.[15]

    • Чтобы записать ответ в численной форме, умножьте 120 x 3,14 = 376,8 см2.

    Реклама

Об этой статье

Эту страницу просматривали 266 138 раз.

Была ли эта статья полезной?

Источник

Площадь круга через радиус

{S = pi r^2}

Здесь вы можете рассчитать площадь круга по известным параметрам. Для вычисления достаточно знать радиус, диаметр круга или длину его окружности.

Содержание:
  1. калькулятор площади круга
  2. отличие окружности от круга
  3. формула площади круга через радиус
  4. формула площади круга через диаметр
  5. формула площади круга через длину окружности
  6. примеры задач

Окружность и круг — в чём отличие?

Часто понятия круг и окружность путают, хотя это разные вещи.

Окружность — это замкнутая линия, а круг — это плоская фигура, ограниченная окружностью. Таким образом, гимнастический обруч или колечко — это окружности, а монета или вкусный блин — это круги.

Круг — бесконечное множество точек на плоскости, которые удалены от заданной точки, называемой центром круга, на значение, не превышающее заданного неотрицательного числа, называемого радиусом этого круга.

Отличие окружности и круга

Формула площади круга через радиус

Площадь круга через радиус

S = pi r^2

r — радиус круга

Формула площади круга через диаметр

Площадь круга через диаметр

S = pi dfrac{d^2}{4}

d — диаметр круга

Формула площади круга через длину окружности

Площадь круга через длину окружности

S = dfrac{L^2}{4pi}

L — длина окружности

Примеры задач на нахождение площади круга

Задача 1

Найдите площадь круга, радиус которого равен 4 см.

Решение

Для решения задачи воспользуемся формулой площади круга через радиус.

S = pi r^2 = pi cdot 4^2 = 16 pi : см^2 approx 50.26548 : см^2

Ответ: 16 pi : см^2 approx 50.26548 : см^2

Полученный ответ удобно проверить с помощью калькулятора .

Задача 2

Найдите площадь круга, радиус которого равен 7 см.

Решение

Задача похожа на предыдущую, поэтому решение будет выглядеть аналогично.

S = pi r^2 = pi cdot 7^2 = 49 pi : см^2 approx 153.93804 : см^2

Ответ: 49 pi : см^2 approx 153.93804 : см^2

Проверим ответ на калькуляторе .

Задача 3

Найдите площадь круга, радиус которого равен 9 см.

Решение

Еще одна типовая задача.

S = pi r^2 = pi cdot 9^2 = 81 pi : см^2 approx 254.469 : см^2

Ответ: 81 pi : см^2 approx 254.469 : см^2

Проверим ответ на калькуляторе .

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти фотографию по первоисточнику
  • Ошибка в данных crc внешний жесткий диск как исправить без форматирования
  • Как найти местоположение другого телефона по номеру
  • Как найти сохраненный черновик в инстаграм
  • Как составить протокол олимпиады