Как найти площадь круга описанного около трапеции - Исправление недочетов и поиск решений вместе с Examum.ru

Свойства окружности, описанной вокруг трапеции

Содержание:

Окружность, описанная около трапеции
Как найти радиус описанной окружности
- Если известны угол и диагональ трапеции
- Если известны диагональ, стороны трапеции и площадь одного из треугольников
- Если известны длины сторон треугольника
Как найти центр описанной окружности
- Если угол прямой
- Если угол острый
- Если угол тупой
Задачи с решениями

Окружность, описанная около трапеции

Трапеция — это выпуклый четырехугольник, две стороны которого параллельны, а две другие — не параллельны.

Около четырехугольника можно описать окружность, если сумма его противолежащих углов равна 180°. Поэтому окружность можно описать только вокруг равнобедренной трапеции.

Окружность, описанная около трапеции

Как найти радиус описанной окружности

Самый распространенный способ найти радиус окружности, описанной около трапеции — через радиус окружности, описанной около треугольника, имеющего 3 любые общие вершины с данной трапецией.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Каждая диагональ делит трапецию на два треугольника. Описанная окружность проходит через все вершины трапеции, значит она проходит через все вершины каждого из этих треугольников и также является для них описанной окружностью.

Как найти радиус описанной окружности

Если известны угол и диагональ трапеции

Формула 1

(R=frac а{2cdotsinalpha},)

где R — радиус описанной окружности,

а — сторона треугольника,

α — угол треугольника, противолежащий стороне а.

Например, если известна диагональ BD=а и острый угол трапеции ABCD ∠CDA=β, то можем найти радиус описанной окружности.

Рассмотрим треугольник BCD. Сторона BD известна. (∠BCD=180°-∠CDA=180°-β).

Радиус описанной окружности будет равен (frac а{2cdotsinleft(180^circ-betaright)}).

Если известны диагональ, стороны трапеции и площадь одного из треугольников

Формула 2

(R=frac{abc}{4S}),

где R — радиус описанной окружности,

а, b, c — стороны треугольника,

S — площадь треугольника.

Если известны длины сторон треугольника

Формула 3

(R=frac{abc}{4sqrt{pleft(p-aright)left(p-bright)left(p-cright)}},)

где R — радиус описанной окружности,

а, b, c — стороны треугольника,

p — ½ периметра треугольника.

Как найти центр описанной окружности

Центр описанной окружности может лежать как внутри трапеции, так и вне ее. Определить его местонахождение помогает угол между диагональю трапеции и боковой стороной.

Если угол прямой

Если диагональ трапеции перпендикулярна ее боковой стороне, то центр описанной окружности будет лежать на середине большего основания. Тогда большее основание будет равно диаметру описанной окружности.

Формула 4

(R=frac12а,)

где R — радиус описанной окружности,

а — большее основание трапеции.

Если угол острый

Если диагональ трапеции и боковая сторона образуют острый угол, то центр описанной около трапеции окружности лежит внутри трапеции.

Если угол тупой

Если диагональ трапеции и боковая сторона образуют тупой угол, то центр описанной около трапеции окружности будет лежать вне трапеции за ее большим основанием.

Задачи с решениями

Задача

Дано: трапеция с описанной окружностью. Периметр трапеции равен 22 см, а ее средняя линия — 5 см.

Найти: боковую сторону трапеции.

Решение: Так как около трапеции описана окружность, эта трапеция — равнобедренная. Удвоенная средняя линия трапеции равна сумме ее оснований (10 см). Сумма двух боковых сторон равна 22-10=12 (см). Боковая сторона трапеции равна 6 см.

Ответ: 6 см.

Примечание

Задача

Дано: основания трапеции ВС=11 см и AD=21 см. Диагональ трапеции ВD=20 см.

Найти: радиус описанной окружности.

Решение: найдем радиус окружности, описанной около (ΔABD. R=frac{BD}{2sinangle A}.)

Трапеция ABCD равнобедренная, AB=CD, так как описать окружность можно только около равнобедренной трапеции.
ВЕ — высота трапеции. Отрезок (АЕ=(21-11):2=5 (см)) по свойству равнобедренной трапеции. Отрезок ЕD=21-5=16 (см).
Треугольник BED прямоугольный. ∠BED=90°. По теореме Пифагора (BE=sqrt{20^2-16^2}=12 (см).)
Треугольник АBE также прямоугольный. ∠BED=90°. По теореме Пифагора (АВ=sqrt{5^2+12^2}=13 (см).)
(sin∠BAD=frac{12}{13}) по определению синуса.
(R=frac{BD}{2sinangle A}=10frac56 (см).)

Ответ: (10frac56 см.)

Источник

Радиус описанной окружности трапеции

Как найти радиус описанной окружности для трапеции?

В зависимости от данных условия, сделать это можно разными способами. Готовой формулы радиуса описанной около трапеции окружности нет.

I. Радиус описанной около трапеции окружности как радиус окружности, описанной около треугольника, вершины которого — вершины трапеции

Описанная около трапеции окружность проходит через все её вершины, следовательно, является описанной для любого из треугольников, вершины которых являются вершинами трапеции.

В общем случае радиус описанной около треугольника окружности может быть найден по одной из формул

где a — сторона треугольника, α — противолежащий ей угол;

либо по формуле

где a, b, c — стороны, S — площадь треугольника.

Для трапеции ABCD радиус может быть найден, например, как радиус окружности, описанной около треугольника ABD:

где синус угла A можно найти из прямоугольного треугольника ABF:

III. Радиус описанной около трапеции окружности как расстояние до точки пересечения серединных перпендикуляров

Радиус описанной окружности — точка пересечения серединных перпендикуляров с сторонам трапеции. (Можно рассуждать иначе: в равнобедренном треугольнике AOD (AO=OD=R) высота ON является также медианой. Для треугольника BOC — аналогично).

Если известна высота трапеции KN=h, основания AD=a, BC=b, можно обозначить ON=x.

Если центр окружности лежит внутри трапеции, OK=h-x, из прямоугольных треугольников ANO и BKO можно выразить

и приравнять правые части

Решив это уравнения относительно x, можно найти R.

IV. Если диагональ трапеции перпендикулярна боковой стороне, центр описанной окружности лежит на середине большего основания и радиус равен половине большего основания.

точка O — середина AD

Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной окружности лежит вне трапеции, за большим основанием.

I вариант нахождения радиуса для этого случая не изменяется.

Во II случае OK=h+x, соответственно, изменяется уравнение для нахождения x и R.

Позже рассмотрим конкретные задачи нахождения радиуса описанной около трапеции окружности.

Трапеция. Формулы, признаки и свойства трапеции

Параллельные стороны называются основами трапеции, а две другие боковыми сторонами

Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.

Основы трапеции — параллельные стороны
Боковые стороны — две другие стороны
Средняя линия — отрезок, соединяющий середины боковых сторон.

Равнобедренная трапеция — трапеция, у которой боковые стороны равны
Прямоугольная трапеция — трапеция, у которой одна из боковых сторон перпендикулярна основам

Основные свойства трапеции

AK = KB, AM = MC, BN = ND, CL = LD

3. Средняя линия трапеции параллельна основаниям и равна их полусумме:

BC : AD = OC : AO = OB : DO

d ₁ 2 + d ₂ 2 = 2 a b + c 2 + d 2

Сторона трапеции

Формулы определения длин сторон трапеции:

a = b + h · ( ctg α + ctg β )

b = a — h · ( ctg α + ctg β )

a = b + c· cos α + d· cos β

b = a — c· cos α — d· cos β

4. Формулы боковых сторон через высоту и углы при нижнем основании:

Средняя линия трапеции

Формулы определения длины средней линии трапеции:

1. Формула определения длины средней линии через длины оснований:

2. Формула определения длины средней линии через площадь и высоту:

Высота трапеции

Формулы определения длины высоты трапеции:

h = c· sin α = d· sin β

2. Формула высоты через диагонали и углы между ними:

h =	sin γ ·	d ₁ d ₂	=	sin δ ·	d ₁ d ₂
a + b	a + b

3. Формула высоты через диагонали, углы между ними и среднюю линию:

h =	sin γ ·	d ₁ d ₂	=	sin δ ·	d ₁ d ₂
2 m	2 m

4. Формула высоты трапеции через площадь и длины оснований:

5. Формула высоты трапеции через площадь и длину средней линии:

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

d ₁ = √ a 2 + d 2 — 2 ad· cos β

d ₂ = √ a 2 + c 2 — 2 ac· cos β

2. Формулы диагоналей через четыре стороны:

d ₁ =	√	d 2 + ab —	a ( d 2 — c 2 )
a — b

d ₂ =	√	c 2 + ab —	a ( c 2 — d 2 )
a — b

d ₁ = √ h 2 + ( a — h · ctg β ) 2 = √ h 2 + ( b + h · ctg α ) 2

d ₂ = √ h 2 + ( a — h · ctg α ) 2 = √ h 2 + ( b + h · ctg β ) 2

d ₁ = √ c 2 + d 2 + 2 ab — d ₂ 2

d ₂ = √ c 2 + d 2 + 2 ab — d ₁ 2

Площадь трапеции

Формулы определения площади трапеции:

1. Формула площади через основания и высоту:

3. Формула площади через диагонали и угол между ними:

S =	d ₁ d ₂	· sin γ	=	d ₁ d ₂	· sin δ
2	2

4. Формула площади через четыре стороны:

S =	a + b	√	c 2 —	(	( a — b ) 2 + c 2 — d 2	)	2
2	2( a — b )

5. Формула Герона для трапеции

S =	a + b	√ ( p — a )( p — b )( p — a — c )( p — a — d )
\| a — b \|

где

p =	a + b + c + d	— полупериметр трапеции.
2

Периметр трапеции

Формула определения периметра трапеции:

1. Формула периметра через основания:

Окружность описанная вокруг трапеции

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d ₁
4√ p ( p — a )( p — c )( p — d ₁)

где

a — большее основание

Окружность вписанная в трапецию

Формула определения радиуса вписанной в трапецию окружности

1. Формула радиуса вписанной окружности через высоту:

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

1. Формула определения длин отрезков проходящих через трапецию:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
2	2	a + b

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Трапеция. Свойства трапеции

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .

Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

Свойства трапеции

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия –

Отношение площадей этих треугольников есть .

4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

Свойства и признаки равнобедренной трапеции

1. В равнобедренной трапеции углы при любом основании равны.

2. В равнобедренной трапеции длины диагоналей равны.

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

Вписанная окружность

Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то

Площадь

или где – средняя линия

Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Чтобы не потерять страничку, вы можете сохранить ее у себя:

источники:

http://ru.onlinemschool.com/math/formula/trapezium/

Трапеция. Свойства трапеции

Источник

Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.

Содержание

Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
- Формула нахождения площади круга через радиус:
- Формула нахождения S-площади круга через D-диаметр:
- Нахождение S круга, если известна длина окружности:
Площадь круга, вписанного в квадрат: формула, примеры решения задач
- Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
- Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
Площадь круга, описанного около квадрата: формула, примеры решения задач
Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
Видео: Математика | Вычисление площадей круга и его частей

Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.

Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач

Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.

Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач

Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.

Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.

Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.

Формула нахождения площади круга через радиус:

Площадь круга: формула через радиус

Примеры решения заданий по нахождению S-площади круга через R-радиус:

————————————————————————————————————————

Задача: Найдите площадь окружности, если ее радиус равен 7 см.

Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².

Ответ: Площадь окружности равна 153,86 см².

Формула нахождения S-площади круга через D-диаметр:

Площадь круга: формула через диаметр

Примеры решения заданий по нахождению S, если известен D:

————————————————————————————————————————-

Задача: Найдите S круга, если его D равен 10 см.

Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².

Ответ: Площадь плоской круглой фигуры равна 78,5 см².

Нахождение S круга, если известна длина окружности:

Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.

Рассмотрим решение на примере задачи:

———————————————————————————————————————-

Задача: Найдите площадь круга, если известна длина окружности L — 12 см.

Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.

Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².

Ответ: Площадь круга равна 11,46 см².

Площадь круга, вписанного в квадрат: формула, примеры решения задач

Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.

Формула нахождения площади круга, вписанного в квадрат:

Площадь круга, вписанного в квадрат: формула

Примеры решения задач по нахождению площади круга, вписанного в квадрат:

———————————————————————————————————————

Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.

Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².

Ответ: Площадь плоской круглой фигуры равна 28,26 см².

————————————————————————————————————————

Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.

Решайте так: Сначала найдем R=a/2=4/2=2 см.

Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².

Ответ: Площадь плоской круглой фигуры равна 12,56 см².

Площадь круга, описанного около квадрата: формула, примеры решения задач

Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.

Формула нахождения S круга, описанного около квадратной фигуры:

Площадь круга, описанного около квадрата: формула

Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:

Задача

Площадь круга, описанного около квадрата: примеры решения задач

Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач

Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.

Формула нахождения площади круга, вписанного в равнобедренный треугольник:

Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула

Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².

Формула нахождения площади круга, вписанного в прямоугольный треугольник:

Площадь круга, вписанного в прямоугольный и равнобедренный треугольник

Примеры решения заданий:

Задача №1

Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: примеры решения задач

Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²

Задача №2

Площадь круга, вписанного в равнобедренный треугольник: примеры решения задач

Решение:

Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: примеры

Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.

Задача №3

Площадь круга, вписанного в треугольник: примеры решения задач

Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач

Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.

Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:

Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула

Примеры решения задач:

Площадь круга, описанного около прямоугольного и равнобедренного треугольника: примеры решения задач

Вот еще пример решения задачи с использованием формулы Герона.

Площадь круга, описанного около прямоугольного и равнобедренного треугольника: примеры

Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.

Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач

У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.

Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.

Для решения этой задачи нужно использовать такие формулы:

Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула

Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:

Площадь круга, вписанного в прямоугольную и равнобедренную трапецию

Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.

Примеры решения задач:

Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: примеры решения задач

Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач

Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:

Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач

Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула

Примеры решения задач:

Площадь круга, описанного около прямоугольной и равнобедренной трапеции: примеры решения задач

Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.

Ответ: Радиус равен 6.

В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.

Видео: Математика | Вычисление площадей круга и его частей

Источник

Светило науки — 7292 ответа — 165986 раз оказано помощи

Найти площадь круга, описанного вокруг трапеции.

Трапеция KTLP;

TL=2 ; KP=14

KT=LP=10.

Ответ: 50π (ед. площади)

Формула площади круга S=πR²

Способ 1) (рис.1)

Проведем высоты трапеции ТМ и LH и продлим их до пересечения с окружностью. T₁L₁=MH=TL=2.

Соединим Т₁ и L₁. Треугольник LL₁T₁ — прямоугольный, => центр — описанной окружности лежит на гипотенузе LT₁.

В ∆ LHP отрезок РН=(КР-MH):2=6

По т.Пифагора LH=8.

По т. о пересекающихся хордах LH•HL₁=PH•HK =>

8•HL₁=6•8 => HL₁=6 => LL₁=8+6=14

По т. Пифагора LT1=√(LL₁²+L₁T₁²)=√(14²+2²)=√200=10√2

R=0.5•10√2=5√2

S=π•5√2)*=50π ед. площади.

Способ 2) (рис.2).

Трапеция равнобедренная. Соединив вершины трапеции L и К, получите треугольник KPL. Формула радиуса описанной около треугольника окружности R=a•b•c:4S, где а, b и с — стороны треугольника, Ѕ — его площадь. Найти радиус, затем искомую площадь круга сможете самостоятельно.

Источник

Окружность вписана в n-угольник, если она касается всех сторон этого n-угольника (рис. 8.106).

Окружность описана около n-угольника, если все вершины n-угольника лежат на окружности (рис. 8.107).

Свойства вписанной окружности

1. Окружность можно вписать в любой треугольник.

2. Окружность можно вписать в четырехугольник, если суммы длин его противолежащих сторон равны.

Например, на рисунке 8.106 .

Так, окружность можно вписать в квадрат и в ромб, но нельзя вписать в параллелограмм и в прямоугольник.

Свойства описанной окружности

1. Окружность можно описать около любого треугольника.

2. Окружность можно описать около четырехугольника, если суммы его противолежащих углов равны.

Например, на рисунке 8.107 $LaTeX formula: angle A+angle C=angle B+angle D=180^{circ}$ .

Так, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.

Расположение центров окружностей, описанных около треугольника:

1) центр окружности расположен на пересечении серединных перпендикуляров к сторонам треугольника;

2) если треугольник остроугольный, то центр окружности расположен в этом треугольнике:

а) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника (центры вписанной и описанной окружностей совпадают (рис. 8.108);

б) в равнобедренном треугольнике центр окружности расположен на биссектрисе, проведенной из вершины треугольника к его основанию (рис. 8.109);

3) если треугольник прямоугольный, то центр окружности расположен на середине гипотенузы (рис. 8.110);

4) если треугольник тупоугольный, то центр окружности расположен вне треугольника (рис. 8.111).

Расположение центров окружностей, вписанных в треугольник:

1) центр окружности, вписанной в треугольник, расположен в этом треугольнике (рис. 8.112 – 8.115);

2) центром окружности является точка пересечения биссектрис треугольника;

3) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника.

Формулы для вычисления радиусов вписанной и описанной окружностей

Радиус окружности, описанной около многоугольника, как правило, обозначают , а радиус окружности, вписанной в многоугольник, обозначают :

1) для равностороннего треугольника со стороной :

$LaTeX formula: R=frac{a}{sqrt{3}}$ , (8.34)

$LaTeX formula: r=frac{a}{2sqrt{3}}$ ; (8.35)

2) для произвольного треугольника со сторонами и площадью :

$LaTeX formula: R=frac{abc}{4S}$ , (8.36)

$LaTeX formula: r=frac{2S}{a+b+c}$ ; (8.37)

3) для прямоугольного треугольника с катетами и гипотенузой :

$LaTeX formula: R=frac{c}{2}$ , (8.38)

$LaTeX formula: r=frac{a+b-c}{2}$ ; (8.39)

4) для квадрата со стороной и диагональю :

$LaTeX formula: R=frac{d}{2}$ , (8.40)

$LaTeX formula: r=frac{a}{2}$ ; (8.41)

5) для прямоугольника с диагональю :

$LaTeX formula: R=frac{d}{2}$ ; (8.42)

6) для ромба с высотой :

$LaTeX formula: r=frac{h}{2}$ ; (8.43)

7) для трапеции с высотой , при условии, что в трапецию можно вписать окружность:

$LaTeX formula: r=frac{h}{2}$ . (8.44)

Если около трапеции можно описать окружность, то, проведя диагональ трапеции и рассмотрев один из полученных треугольников со сторонами и площадью , по формуле $LaTeX formula: R=frac{abc}{4S}$ найдем радиус окружности описанной около треугольника, а значит и около трапеции (рис. 8.116);

для правильного шестиугольника со стороной :

, (8.45)

$LaTeX formula: r=frac{asqrt{3}}{2}$ . (8.46)

Правильный шестиугольник состоит из шести правильных треугольников (рис. 8.117) и точка является центром вписанной в него и описанной около него окружностей.

Пример 1. Найдите сторону квадрата, если известно, что разность между площадью квадрата и площадью вписанного в него круга равна .

Решение. Так как площадь круга радиуса находят по формуле 8.32, а площадь квадрата со стороной находят по формуле $LaTeX formula: S=a^{2}$ , то согласно условию задачи запишем: $LaTeX formula: S_{square }-S_{bigcirc }=12$ , $LaTeX formula: pi r^{2}-a^{2}=2pi -8$ .

А так как $LaTeX formula: r=frac{a}{2}$ , то $LaTeX formula: frac{pi a^{2}}{4}-a^{2}=2pi -8$ , $LaTeX formula: pi a^{2}-4a^{2}=4(2pi -8)$ , $LaTeX formula: a^{2}(pi -4)=8(pi -4)$ , $LaTeX formula: a^{2}=8$ , .

Ответ: .

Пример 2. Площадь прямоугольника равна 4, а разность длин его смежных сторон рана 3. Найдите радиус окружности, описанной около этого прямоугольника.

Решение. Площадь прямоугольника со смежными сторонами и находят по формуле .

Пусть , тогда (рис. 8.118).

Получим: , $LaTeX formula: x^{2}+3x-4=0$ , откуда , следовательно, , .

По теореме Пифагора найдем диагональ прямоугольника: $LaTeX formula: d^{2}=1+16=17$ , . Согласно формуле 8.42 .

Ответ: .

Пример 3. Найдите радиус окружности, вписанной в ромб, если его диагонали равны 6 и 8.

Решение. По теореме Пифагора найдем сторону ромба (рис. 8.119):

$LaTeX formula: a^{2}=left (frac{d_{1}}{2} right )^{2}+left ( frac{d_{2}}{2} right )^{2}$ , $LaTeX formula: a^{2}=3^{2}+4^{2}$ , .

По формуле 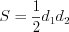$LaTeX formula: S=frac{1}{2}d_{1}d_{2}$ найдем площадь ромба: $LaTeX formula: S=frac{1}{2}cdot 6cdot 8=24$ .

Но площадь ромба можно найти и по формуле , а так как , то . Тогда , а .

Ответ: 2,4.

Пример 4. Найдите длину окружности, вписанной в правильный треугольник, если его площадь равна .

Решение. Площадь правильного треугольника со стороной находят по формуле: $LaTeX formula: S=frac{sqrt{3}a^{2}}{4}$ .

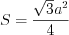
Зная площадь треугольника, найдем его сторону: $LaTeX formula: frac{sqrt{3}a^{2}}{4}=4sqrt{3}$ , $LaTeX formula: a^{2}=16$ , .

По формуле 8.35 найдем радиус окружности, вписанной в этот треугольник: $LaTeX formula: r=frac{4}{2sqrt{3}}=frac{2}{sqrt{3}}$ .

По формуле 8.30 найдем длину окружности: $LaTeX formula: C=frac{4pi }{sqrt{3}}$ .

Ответ: $LaTeX formula: frac{4sqrt{3}pi }{3}$ .

Пример 5. Радиус окружности, описанной около равнобедренного прямоугольного треугольника равен 2. Найдите радиус окружности, вписанной в этот треугольник.

Решение. Радиус окружности, описанной около прямоугольного треугольника с гипотенузой находят по формуле 8.38. Тогда .

Так как треугольник равнобедренный, то его катеты и раны и по теореме Пифагора $LaTeX formula: c^{2}=2a^{2}$ , откуда $LaTeX formula: a=frac{C}{sqrt{2}}$ , $LaTeX formula: a=frac{4}{sqrt{2}}=2sqrt{2}$ .

Радиус окружности, вписанной в прямоугольный треугольник, находят по формуле 8.39. В нашем случае $LaTeX formula: r=frac{2a-c}{2}$ , $LaTeX formula: r=frac{4sqrt{2}-4}{2}=2sqrt{2}-2$ .

Ответ: .

Пример 6. Один из катетов прямоугольного треугольника равен 8, а радиус окружности, вписанной в треугольник равен 3. Найдите площадь треугольника.

Решение. Рассмотрим прямоугольный треугольник . Точка является центром вписанной в треугольник окружности (рис. 8.120).

Так как радиусы вписанной в треугольник окружности перпендикулярны сторонам треугольника в точках касания, то имеем квадрат со стороной 3. Если катет , а сторона квадрата , то .

Пусть отрезок . По свойству касательных и .

Тогда по теореме Пифагора $LaTeX formula: BC^{2}=AC^{2}+AB^{2}$ или $LaTeX formula: 25+10x+x^{2}=64+9+6x+x^{2}$ , откуда , .

Найдем катет : .

Найдем площадь треугольника: $LaTeX formula: S_{Delta ABC}=frac{1}{2}cdot ACcdot AB$ , $LaTeX formula: S_{Delta ABC}=frac{1}{2}cdot 8cdot 15=60$ .

Ответ: 60.

Пример 7. Окружность, центр которой расположен на большей стороне треугольника, делит эту сторону на отрезки 4 и 8 и касается двух других его сторон, длина одной из которых равна 6. Найдите радиус окружности, вписанной в этот треугольник (рис.8.121).

Решение. Согласно свойству биссектрисы треугольника запишем: $LaTeX formula: frac{6}{4}=frac{x}{8}$ , откуда .

Радиус окружности, вписанной в треугольник, найдем по формуле 8.37.

В свою очередь по формуле Герона найдем площадь треугольника. Так как , то .

Тогда $LaTeX formula: r=frac{18sqrt{15}}{30}=frac{3sqrt{15}}{5}=0,6sqrt{15}$ .

Ответ: .

Пример 8. В прямоугольную трапецию вписана окружность радиуса 3, которая в точке касания делит ее боковую сторону на отрезки 4 и 5. Найдите площадь трапеции.

Решение. Согласно условию задачи и рисунку 8.122, запишем: , .

По свойству четырехугольника, описанного около окружности, получим: , , .

Согласно формуле 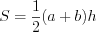$LaTeX formula: S=frac{1}{2}(a+b)h$ найдем площадь трапеции: $LaTeX formula: S=frac{1}{2}cdot 15cdot 6=45$ .

Ответ: 45.

Пример 9. Длины оснований равнобедренной трапеции относятся как , а длина ее высоты равна 17. Вычислите площадь круга, описанного около трапеции, если известно, что средняя линия трапеции равна ее высоте.

Решение. Рассмотрим равнобедренную трапецию (рис. 8.123) и проведем диагональ трапеции .

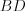
Радиус окружности, описанной около треугольника , найдем по формуле 8.36:

$LaTeX formula: R=frac{ABcdot BDcdot AD}{4cdot S_{triangle ABD}}=frac{ABcdot BDcdot AD}{4cdot frac{1}{2}cdot ADcdot BN}$ , $LaTeX formula: R=frac{ABcdot BD}{2cdot BN}$ .

Зная, что и вводя коэффициент пропорциональности , получим , .

Так как длина средней линии трапеции равна высоте трапеции, то $LaTeX formula: frac{1}{2}(5k +12k)=17$ , откуда . Тогда , .

Поскольку четырехугольник является прямоугольником, то , тогда $LaTeX formula: AN=KD=frac{1}{2}(24-10)=7$ .

Согласно теореме Пифагора запишем:

$LaTeX formula: AB=sqrt{AN^{2}+BN^{2}}$ , $LaTeX formula: AB=sqrt{17^{2}+7^{2}}=sqrt{338}$ ;

$LaTeX formula: BD=sqrt{BN^{2}+ND^{2}}$ , $LaTeX formula: BD=sqrt{17^{2}+17^{2}}=17sqrt{2}$ .

По формуле 8.36 найдем радиус окружности, описанной около треугольника , а, следовательно, и около трапеции :

$LaTeX formula: R=frac{sqrt{338}cdot 17sqrt{2}}{2cdot 17}=frac{2cdot 13}{2}=13$ .

Согласно формуле 8.32 найдем площадь круга: .

Ответ: .

Пример 10. В правильный шестиугольник вписана окружность и около него описана окружность. Найдите площадь образовавшегося кольца, если сторона шестиугольника равна .

Решение. По формуле 8.45 найдем радиус окружности, описанной около правильного шестиугольника: .

По формуле 8.46 найдем радиус окружности, вписанной в этот шестиугольник. Так как , то $LaTeX formula: r=frac{3}{2}$ .

Площадь круга находят по формуле 8.32. Тогда $LaTeX formula: S_{1}=3pi$ , а $LaTeX formula: S_{2}=frac{9pi}{4}$ .

Найдем площадь кольца: $LaTeX formula: S_{K}=S_{1}-S_{2}$ , $LaTeX formula: S_{K}=3pi -frac{9pi }{4}=frac{3pi }{4}$ .

Ответ: .

1. В любой треугольник можно вписать окружность и около любого треугольника можно описать окружность.

2. Не во всякий четырехугольник можно вписать окружность. Например, окружность можно вписать в ромб и квадрат, но нельзя вписать в параллелограмм и прямоугольник.

3. Не около всякого четырехугольника можно описать окружность. Например, окружность можно описать около квадрата и прямоугольника, но нельзя описать около параллелограмма и ромба.

4. Не во всякую трапецию можно писать окружность и не около всякой трапеции можно описать окружность. Описать окружность можно только около равнобедренной трапеции.

5. Если многоугольник правильный (все его стороны и все его углы равны между собой), то в него всегда можно вписать окружность и около него всегда можно описать окружность. Причем, центры этих окружностей совпадают.

Длину окружности радиуса находят по формуле:

. (8.30)

Площадь круга радиуса находят по формуле:

$LaTeX formula: S=pi R^{2}$ . (8.32)

Источник