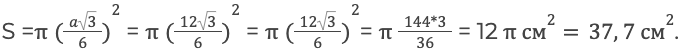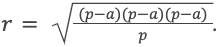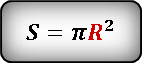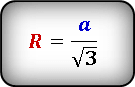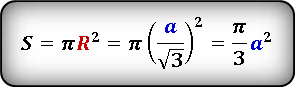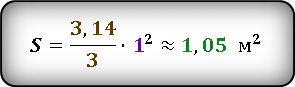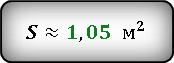Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
Площадь равностороннего треугольника через стороны
Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
Площадь круга, вписанного в равносторонний треугольник: решение
Содержание:
В геометрии встречаются понятия описанной и вписанной геометрических фигур. Описанным будет треугольник, через вершины которого проходит окружность, вписанным – если его стороны соприкасаются с кругом. Такое построение в обоих случаях обладает рядом особенностей, которые применяются на практике и упрощают решение задач. Рассмотрим свойства и формулы для расчёта описанного 3-угольника.
Особенности явления
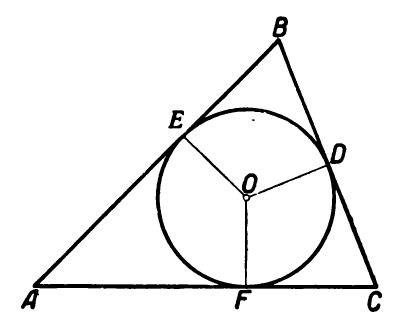
Окружность с центром O, проходящая через одну из точек: D, E либо F обязательно будет лежать и на двух остальных. Прямые, разделяющие углы пополам, или биссектрисы равностороннего треугольника пересекаются в общей точке – центре вписанной окружности, который находится на одинаковом удалении от сторон геометрической фигуры.
Из вышесказанного следуют свойства:
- В треугольник вписывается лишь один круг.
- Его центр находится на одинаковом расстоянии от ближайших точек на сторонах 3-угольника.
- Перпендикуляры, опущенные из центра O, и биссектрисы пересекаются в одной точке, называемой центром вписанной окружности.
Способ вычислить площадь круга, вписанного в треугольник
Для вычисления площади, если дан только размер стороны правильного треугольника, применяется ряд формул.
S=πr 2 .
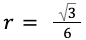
- a – длина стороны геометрической фигуры;
- r – радиус круга, расположенного внутри многоугольника с тремя равными сторонами.
После подстановки значения получается выражение для вычисления площади вписанной окружности:
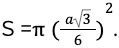
В задачах могут давать длину сторон, тогда 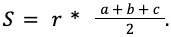
Выражение 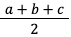
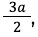
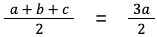
Зная это, формула записывается в виде: S = r * p.
Задачи
В формулу подставим длину сторон треугольника, после вычислений получим результат.
Вычислить занимаемое вписанным в 3-угольник кругом пространство, если его сторона равна 10 см.
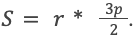
Известно, что он определяется по формуле:
После преобразований выражение упрощается до 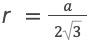
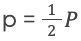
Начинаем проводить вычисления.
P = a + a + a = 10 +10 +10 или 10 * 3 = 30 см.
Быстро найти формулу для расчета онлайн.
Условие задачи:
Прямоугольный треугольник АВС вписан в окружность Найти площадь круга, ограниченного этой окружностью, если размер клеток составляет 1см на 1см.
Дано:
Размер клетки, = 1 см на 1 см
Пояснение к рисунку:
O — центр окружности
К — вершина прямого угла, достроенного прямоугольного треугольника
D — диаметр описанной окружности
c — гипотенуза треугольника
Найти площадь круга: S
Суть всего решения сводится к тому, что:
— первое , достроенный треугольник АСК, имеет смежную гипотенузу с треугольником АВС и является также вписанным в окружность и прямоугольным. А у этого треугольника мы можем уже точно определить его катеты АК=13клеток=13см и КС=5клеток=5см.
— второе , как известно, если прямоугольный треугольник вписан в окружность, то его гипотенуза равна диаметру окружности. Это так же видно и из чертежа.
Для определения площади круга, используем следующую формулу через диаметр, который необходимо найти.
А как уже было сказано выше, диаметр окружности равен гипотенузе.
По теореме Пифагора, находим гипотенузу, т. е. диаметр окружности.
Подставляем полученное выражение в формулу площади круга.
Вставляем значения и вычисляем результат.
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
http://bingoschool.ru/manual/ploshhad-kruga-vpisannogo-v-ravnostoronnij-treugolnik-reshenie/
http://www-formula.ru/81-zadachi/area/list-circle/circle
Расчёт площади круга вписанного в равносторонний треугольник, по стороне треугольника
Калькулятор рассчитывает площадь круга вписанного в равносторонний треугольник, по стороне треугольника.
Введите сторону равностороннего треугольника a
Формула площади круга вписанного в равносторонний треугольник, по стороне треугольника
Где S — площадь круга,
a — сторона треугольника,
π=3.14
Вывод формулы площади круга вписанного в равносторонний треугольник, по стороне треугольника
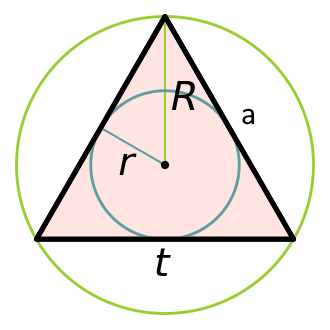
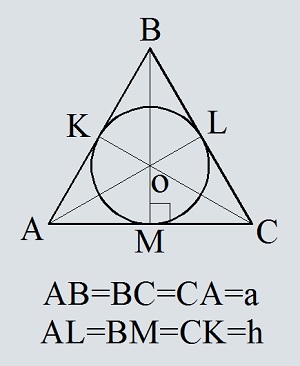
В равностороннем треугольнике каждая медиана совпадает с биссектрисой и высотой. Все они пересекаются в одной точке и делятся ею в отношении 1:2. Эта точка является центром окружности вписанной в этот треугольник.
Т.к. BM=h перепишем формулу выше
h мы вычислим по теореме пифагора из треугольника ABM. AB=a; AM=a/2
Подставим в формулу площади круга радиус через h
Подставим выведенную ранее высоту h
Похожие калькуляторы
Условие задачи:
Равносторонний треугольник со стороной 1 м вписан в окружность. Найти площадь круга, ограниченного этой окружностью.
Дано:
Сторона треугольника, a = 1 м
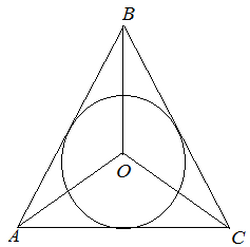
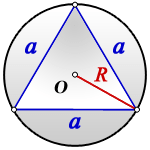
Пояснение к рисунку:
O — центр окружности
R — радиус описанной окружности
Найти площадь круга: S
Решение
Используем формулу площади круга через радиус. Но пока он нам не известен, его надо найти.
Определить радиус, нам поможет следующая формула. В ней радиус окружности выражен через сторону вписанного треугольника.
Подставим радиус выраженный через сторону и преобразовав, получим следующие выражение.
Подставим значения.
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Ответ:
Калькулятор для расчета площади круга
- Подробности
-
Опубликовано: 15 сентября 2017
-
Обновлено: 13 августа 2021




Вписанного в равносторонний треугольник
Формула расчёта площади круга вписанного в равносторонний треугольник Вам необходимо указать сторону равностороннего треугольника (a).
Расчёт происходит по формуле 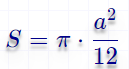
| Сторона равностороннего треугольника (a) |
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.
Оставить комментарий
Заполните все поля.
Ваше имя:
| Оценка |
Как найти площадь круга
Задачи на вычисление площади той или иной геометрической фигуры приходится решать школьнику и студенту, землемеру и архитектору, закройщику и токарю. Площадь круга можно вычислить разными способами, в зависимости от того, какими данными вы располагаете.

Кругом называется часть плоскости, ограниченная окружностью. Основным показателем и для окружности, и для круга является радиус. Если он задан, площадь круга можно вычислить по основной формуле S=πR2, где S – площадь круга, R – радиус окружности, ограничивающей круг, а π – константа, равная 3,14. В условиях задачи может быть дана длина окружности. Она равна L=2πR. В этом случае сначала необходимо вычислить радиус, разделив заданную величину L на 2π, то есть воспользоваться формулой R=L/2π.
В окружность, ограничивающую круг, может быть вписан четырехугольник, сумма противолежащих углов которого составляет 180°, то есть это квадрат или прямоугольник. В этом случае диаметр описанной вокруг четырехугольника окружности является одновременно диагональю. Если в условиях заданы размеры сторон четырехугольника, найти эту диагональ не составит особого труда, воспользовавшись теоремой Пифагора. Диагональ делит квадрат или прямоугольник на два прямоугольных треугольника, то есть является гипотенузой каждого из этих треугольников. Соответственно, найти ее можно, сложив квадраты сторон четырехугольника, то есть по формуле d2=a2+b2. Чтобы найти площадь круга, даже не нужно из полученного результата извлекать квадратный корень, поскольку R=d/2. Чтобы найти квадрат радиуса, достаточно квадрат диаметра разделить на 4.
Способ решения этого варианта задачи зависит от того, какой треугольник вписан и какие его параметры заданы. Если треугольник прямоугольны, алгоритм решения будет таким же, как для квадрата или прямоугольника, поскольку сторона, противолежащая прямому углу, всегда является диаметром описанной окружности. Если даны размеры катетов, возведите каждый из них в квадрат и найдите сумму, а затем полученный результат разделите на 4 и умножьте на число π. Если треугольник равносторонний, придется выполнить несколько дополнительных построений, чтобы в итоге получились прямоугольные треугольники, параметры которых вам известны. Например, в окружность с центром О вписан равносторонний треугольник АВС, сторона которого вам задана. Проведите высоты AN, ВM и СQ. Рассмотрите, например, прямоугольный треугольник AQO. Вам известна его гипотенуза AQ, которая равна половине стороны исходного треугольника, а также все углы, так что найти длину отрезка AQ, который одновременно является радиусом круга, площадь которого вам надо найти, можно по теореме синусов или косинусов.
Видео по теме