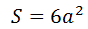Как найти площадь куба если известен объем

Площадь поверхности куба

  1. Главная
  2. /
  3. Математика
  4. /
  5. Геометрия
  6. /
  7. Площадь поверхности куба

Чтобы посчитать площадь поверхности куба воспользуйтесь нашим очень удобным онлайн калькулятором:

Онлайн калькулятор

Площадь поверхности куба через ребро
Чему равна площадь поверхности куба, если:

длина ребра a =

Sпов =

0

Округление ответа:

Площадь поверхности куба через диагональ
Чему равна площадь поверхности куба, если:

длина диагонали d =

Sпов =

0

Округление ответа:

Площадь поверхности куба через объем
Чему равна площадь поверхности куба, если:

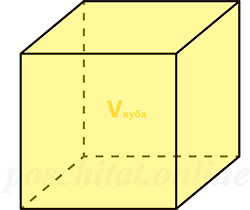
объём Vкуба =

Sпов =

0

Округление ответа:

Теория

Площадь поверхности куба через ребро

Чему равна площадь поверхности куба Sпов, если длина его ребра a:

Формула

Sпов = 6 ⋅ a²

Пример

Для примера, посчитаем чему равна площадь поверхности куба, если он имеет длину рёбер a = 5 см :

Sпов = 6 ⋅ 5² = 6 ⋅ 25 = 150 см²

Площадь поверхности куба через диагональ

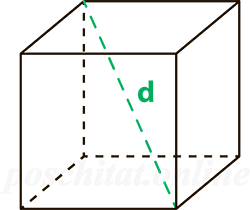
Чему равна площадь поверхности куба Sпов, если длина диагонали этого куба d:

Формула

Sпов = 2 ⋅ d²

Пример

Для примера, посчитаем чему равна площадь поверхности куба, если длина диагонали у него d = 3 м:

Sпов = 2 ⋅ 3² = 2 ⋅ 9 = 18 м² = 180 000 см²

Площадь поверхности куба через объем

Чему равна площадь поверхности куба Sпов, если объём куба Vкуба:

Формула

Sпов = 6 ⋅ ³√Vкуба²

Пример

Для примера, посчитаем чему равна площадь поверхности куба, если его объём Vкуба = 8 см³:

Sпов = 6 ⋅ 3√8² = 6 ⋅3√64 = 6 ⋅ 4 = 24 см²

См. также

Источник

При помощи нашего калькулятора вы легко сможете узнать площадь куба.

Для того что бы вычислить площадь куба необходимо знать длину его ребра. Если нам известна указанная величина, для нас не составит труда вычислить площадь.
Площадь куба рассчитывается по следующей формуле:

S=6a2 или S=6a * a

Где S – площадь, a – длина ребра куба.

Для того, что бы вычислить площадь куба зная его объем необходимо совершить следующие действия:

  1. Вычислить длину сторон куба это делается по следующей формуле
  2. Зная длину сторон куба мы используем формулу приведенную выше

    3. S=6a2 или S=6a * a

Где S – площадь, V — Объем куба, a – длина ребра куба.

Источник

Формулировка задачи: Объем куба равен V. Найдите площадь его поверхности.

Задача входит в состав ЕГЭ по математике базового уровня для 11 класса под номером 13 (Задачи по стереометрии).

Рассмотрим, как решаются подобные задачи на примере и выведем общий способ решения.

Пример задачи:

Объем куба равен 8. Найдите площадь его поверхности.

Решение:

Сторону куба можно получить из его объема:

Теперь можно вычислить площадь поверхности куба по его стороне:

S = 6 ⋅ a2 = 6 ⋅ 22 = 24

Ответ: 24

В общем виде решение данной задачи по стереометрии выглядит следующим образом:

a = ∛V – сторона куба

S = 6a2 = 6 ⋅ (∛V)2

где V – объем куба.

Остается лишь подставить конкретные значения и подсчитать результат.

Поделитесь статьей с одноклассниками «Дан объем куба, найдите площадь его поверхности – как решать».

При копировании материалов с сайта ссылка на источник обязательна. Уважайте труд людей, которые вам помогают.
Нашли ошибку? Выделите текст и нажмите Ctrl + Enter.

Источник

Онлайн калькулятор площади поверхности куба поможет найти площадь куба пятью различными формулами. Выбор неоходимой формулы зависит от исходных данных. 
Выполнив расчет на этом онлайн калькуляторе площади поверхности куба Вы сможете получить не только ответ но еще и детальное пошаговое решение, тем самым закрепите знания в данном материале.

  • Калькулятор
  • Инструкция
  • Теория
  • История
  • Сообщить о проблеме

Распечатать

Способ расчета площади куба:

Сторона а:

Куб

Куб (или гексаэдр) — это правильный многогранник, который состоит из многоугольников, являющихся квадратами.
Формула площади поверхности куба Формула площади поверхности куба По стороне
где a — сторона куба

Решение:

S = 6a2

= 6·82

= 6·64

=

384

Ответ: Площадь поверхности куба со стороной 8 равна 384

Куб – это геометрическая фигура, которую еще называют правильным многогранником, каждая из его граней напоминает квадрат, при этом все ребра этой фигуры между собой равны.

Скачать все формулы нахождения площади поверхности куба в формате Word/PDF

Похожие калькуляторы

  • Площадь поверхности призмы онлайн калькулятор

  • Площадь поверхности параллелепипеда онлайн калькулятор

  • Площадь боковой поверхности цилиндра онлайн калькулятор (2 способа)

  • Площадь поверхности цилиндра онлайн калькулятор (2 способа)

  • Площадь поверхности конуса онлайн калькулятор

Калькуляторы других категорий

  • Деление в столбик онлайн. Калькулятор наглядного деления.

  • Сторона треугольника 14 формул расчет онлайн

  • Перевод чисел из одной системы счисления в любую другую онлайн

  • Сложение, умножение и деление чисел в различных системах счисления

  • Умножение в столбик онлайн. Калькулятор наглядного умножения.

Ваша оценка?
Источник

Площадь поверхности куба через ребро

{S_{полн}=6a^2}

На этой странице мы собрали формулы, которые помогут найти площадь полной и боковой поверхности куба. А чтобы упростить расчет у нас есть калькулятор, который сделает это быстро и точно.

В дополнение на сайте можно найти объем куба.

Куб — фигура, представляющая собой правильный многогранник, все грани которого являются квадратами. Все ребра (стороны) куба равны между собой.

Содержание:
  1. калькулятор площади поверхности куба
  2. площадь полной поверхности куба
  3. формула площади полной поверхности куба через ребро
  4. формула площади полной поверхности куба через диагональ грани
  5. формула площади полной поверхности куба через диагональ куба
  6. формула площади полной поверхности куба через периметр грани
  7. формула площади полной поверхности куба через периметр куба
  8. формула площади полной поверхности куба через объем
  9. формула площади полной поверхности куба через площадь вписанного шара
  10. площадь боковой поверхности куба
  11. формула площади боковой поверхности куба через ребро
  12. формула площади боковой поверхности куба через диагональ грани
  13. формула площади боковой поверхности куба через диагональ куба
  14. формула площади боковой поверхности куба через периметр грани
  15. формула площади боковой поверхности куба через периметр куба
  16. формула площади боковой поверхности куба через объем
  17. примеры задач

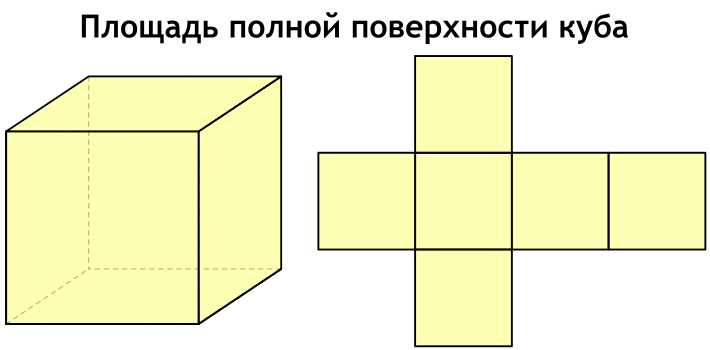
Что такое площадь полной поверхности куба

Куб состоит из сторон, которые называют гранями. Каждая такая грань представляет собой квадрат, а всего у куба 6 граней. Площади всех этих граней равны между собой и сложив все площади всех шести граней куба мы получим площадь полной поверхности куба.

Площадь полной поверхности куба – это сумма площадей всех его граней.

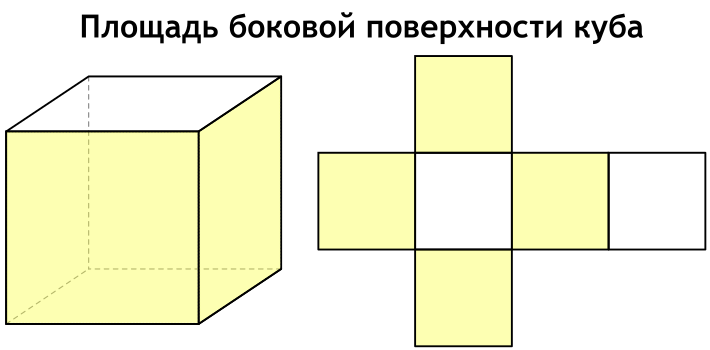
Площадь полной поверхности удобно представить, если посмотреть на развертку куба.

Площадь полной поверхности куба

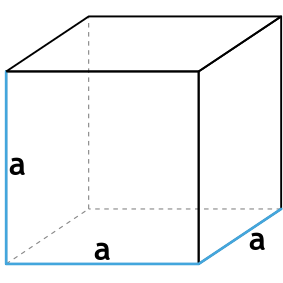
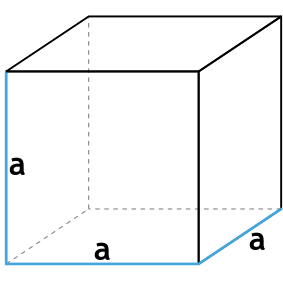
Формула площади полной поверхности куба через ребро

Площадь полной поверхности куба через ребро

{S_{полн}=6a^2}

a — ребро куба

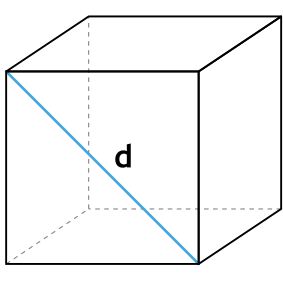
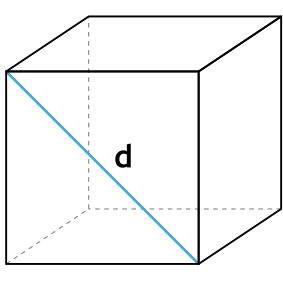
Формула площади полной поверхности куба через диагональ грани

Площадь полной поверхности куба через диагональ грани

{S_{полн}=3d , ^2}

d — диагональ грани куба

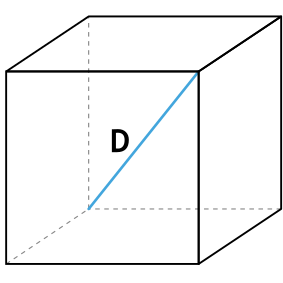
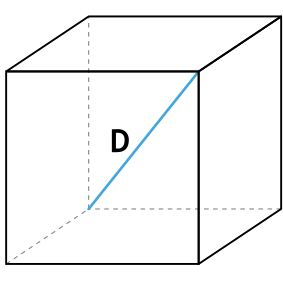
Формула площади полной поверхности куба через диагональ куба

Площадь полной поверхности куба через диагональ куба

{S_{полн}=2D^2}

D — диагональ куба

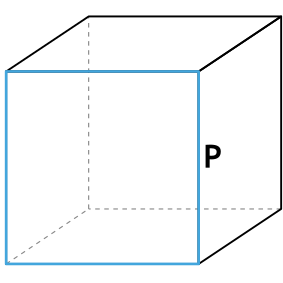
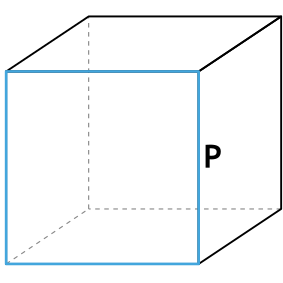
Формула площади полной поверхности куба через периметр грани

Площадь полной поверхности куба через периметр грани

{S_{полн}= dfrac{3}{8}P^2}

P — периметр грани куба

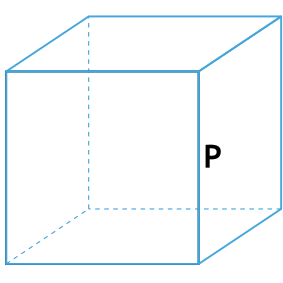
Формула площади полной поверхности куба через периметр куба

Площадь полной поверхности куба через периметр куба

{S_{полн}= dfrac{P^2}{24}}

P — периметр куба

Формула площади полной поверхности куба через объем

Площадь полной поверхности куба через объем

{S_{полн}= 6{(sqrt[3]{V})}^2}

V — объем куба

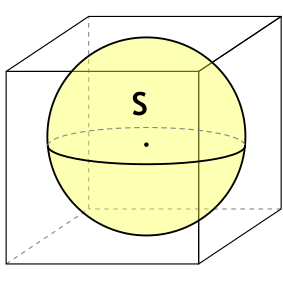
Формула площади полной поверхности куба через площадь вписанного шара

Площадь полной поверхности куба через площадь вписанного шара

{S_{полн}= 6 dfrac{S}{pi}}

S — площадь вписанного в куб шара

Что такое площадь боковой поверхности куба

Боковая поверхность куба — сумма площадей всех его боковых граней, которых у куба четыре.

Площадь боковой поверхности куба

Формула площади боковой поверхности куба через ребро

Площадь боковой поверхности куба через ребро

{S_{бок} = 4a^2}

a — ребро куба

Формула площади боковой поверхности куба через диагональ грани

Площадь боковой поверхности куба через диагональ грани

{S_{бок}=2d , ^2}

d — диагональ грани куба

Формула площади боковой поверхности куба через диагональ куба

Площадь боковой поверхности куба через диагональ куба

{S_{бок}=dfrac{4}{3}D^2}

D — диагональ куба

Формула площади боковой поверхности куба через периметр грани

Площадь боковой поверхности куба через периметр грани

{S_{бок}= dfrac{P^2}{4}}

P — периметр грани куба

Формула площади боковой поверхности куба через периметр куба

Площадь боковой поверхности куба через периметр куба

{S_{бок}= dfrac{P^2}{36}}

P — периметр куба

Формула площади боковой поверхности куба через объем

Площадь боковой поверхности куба через объем

{S_{бок}= 4{(sqrt[3]{V})}^2}

V — объем куба

Примеры задач на нахождение площади поверхности куба

Задача 1

Найдите площадь поверхности куба, если его объем равен 125см³.

Решение

Для нахождения площади полной поверхности куба через его объем, нам поможет эта формула.

S_{полн} = 6{(sqrt[3]{V})}^2 = 6{(sqrt[3]{125})}^2 = 6{(5)}^2 = 6 cdot 25 = 150 : см²

Ответ: 150 см²

Проверить ответ нам поможет калькулятор .

Задача 1

Найдите площадь боковой поверхности куба с ребром 4см.

Решение

Для нахождения площади боковой поверхности куба с известной длиной ребра используем эту формулу.

S_{бок} = 4a^2 = 4 cdot 4^2 = 4 cdot 16 = 64 : см²

Ответ: 64 см²

Проверка .

Источник

Понравилась статья? Поделить с друзьями:
  • Кассовая отчетность как составить
  • Как составить порядок по взаимодействию
  • Как составить лабораторно практическую работу
  • Как составить письменное обращение в министерство здравоохранения
  • Как найти удивительные качели в аватарии