Как найти площадь квадрата если известна диагональ - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

Наиболее распространенной формулой для вычисления площади квадрата является следующая: S = a². Но иногда в задаче дана только диагональ квадрата, то есть отрезок, соединяющий противоположные вершины. Если вы знакомы с прямоугольными треугольниками, для вычисления площади квадрата можно воспользоваться формулой, которая включает диагональ.

1

Нарисуйте квадрат. У квадрата четыре равные стороны.^[1] Допустим, что длина каждой стороны равна а.
2

Посмотрите на основную формулу для вычисления площади квадрата. Площадь квадрата равна произведению длины на ширину. Так как каждая сторона квадрата равна а, формула для вычисления площади квадрата: S = а х а = а². Эта формула понадобится далее.
3

Соедините два противоположных угла квадрата, чтобы провести диагональ. Допустим, что длина диагонали равна d. Диагональ делит квадрат на два прямоугольных треугольника.
4
К одному из треугольников примените теорему Пифагора. По теореме Пифагора^[2] можно найти гипотенузу (самую длинную сторону) прямоугольного треугольника: $a^{2}+b^{2}=c^{2}$ , где а и b — катеты, с — гипотенуза. Разделив квадрат на два прямоугольных треугольника, примените эту формулу к одному из них.
- Катетами прямоугольного треугольника являются стороны квадрата, каждая из которых равна а.
- Гипотенузой является диагональ квадрата, равная d.
- $a^{2}+a^{2}=d^{2}$
5

Изолируйте а² на одной стороне формулы. Помните, что согласно основной формуле для вычисления площади квадрата, она равна а². Если изолировать а² на одной стороне формулы, можно вывести новую формулу для вычисления площади квадрата.
6

Воспользуйтесь этой формулой для решения задачи. Полученную формулу S = ${frac {d^{2}}{2}}$ можно применять к любым квадратам: просто подставьте в нее значение диагонали (вместо d).

Реклама

1

Найдите диагональ по стороне.^[3] Если сторона квадрата равна а, а диагональ равна d, теорема Пифагора запишется так: $2a^{2}=d^{2}$ . По этой формуле можно вычислить диагональ, если сторона квадрата известна.
2
3
Проверьте правильность формулы. Верность математического вывода формулы S = ${frac {d^{2}}{2}}$ не вызывает сомнений, но можно ли проверить правильность формулы наглядно? Допустим, что сторона второго квадрата равна d, то есть диагонали первого квадрата; тогда площадь второго квадрата равна $d^{2}$ . Так как формула для вычисления площади S = ${frac {d^{2}}{2}}$ , можно заключить, что площадь второго квадрата в два раза больше площади первого квадрата. Проверьте это наглядно:
- На бумаге нарисуйте первый квадрат. Убедитесь, что все стороны равны.
- Измерьте диагональ. Нарисуйте второй квадрат: каждая его сторона должна быть равна диагонали первого квадрата.
- Нарисуйте копию первого квадрата, а затем вырежьте три квадрата.
- Разрежьте два меньших квадрата так, чтобы они поместились в большем квадрате. Два меньших квадрата должны полностью покрыть больший квадрат, что доказывает, что площадь большего квадрата в два раза больше площади меньшего квадрата.
Реклама

Советы

Если калькулятора нет, но необходимо получить точное значение √2, извлеките корень вручную. Например, примените метод Ньютона-Рафсона.^[4]
Приведенная формула используется во многих областях, в том числе в кристаллографии, химии и технике. Например, при помощи этой формулы можно вычислить площадь ландшафта, который виден воочию или на фотографии/рисунке. Для этого измерьте пройденный путь, а затем проведите воображаемую диагональ.
Если вы предпочитаете изучать математику с наглядными примерами или хотите узнать, как использовать диаграммы и графики в искусстве, читайте статьи на сайте wikiHow (например, в категориях «Математика», «Графические программы», «Офисные программы» и других).

Об этой статье

Эту страницу просматривали 50 770 раз.

Была ли эта статья полезной?

Источник

{S = a ^2}

На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.

Квадрат — четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.

Содержание:

калькулятор площади квадрата
формула площади квадрата через сторону
формула площади квадрата через диагональ
формула площади квадрата через радиус вписанной окружности
формула площади квадрата через радиус описанной окружности
формула площади квадрата через периметр
примеры задач

Формула площади квадрата через сторону

S = a ^2

a — сторона квадрата

Формула площади квадрата через диагональ

S=dfrac{d^2}{2}

d — диагональ квадрата

Формула площади квадрата через радиус вписанной окружности

S = 4r^2

r — радиус вписанной окружности

Формула площади квадрата через радиус описанной окружности

S = 2R^2

R — радиус описанной окружности

Формула площади квадрата через периметр

S = dfrac{P^2}{16}

P — периметр квадрата

Примеры задач на нахождение площади квадрата

Задача 1

Найдите площадь квадрата если его диагональ равна 1.

Решение

Для решения задачи воспользуемся формулой.

S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2

Ответ: 0.5 см²

Проверим ответ на калькуляторе .

Задача 2

Найдите площадь квадрата, описанного вокруг окружности радиуса 83.

Решение

Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.

S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2

Ответ: 13778 см²

Проверим ответ с помощью калькулятора .

Задача 3

Найдите площадь квадрата если его сторона равна 8 см.

Решение

Используем первую формулу.

S = a ^2 = 8 ^2 = 64 : см^2

Ответ: 64 см²

Проверим результат на калькуляторе .

Задача 4

Найдите площадь квадрата периметр которого равен 456 см.

Решение

Используем формулу для площади квадрата через периметр.

S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2

Ответ: 12996 см²

Проверка .

Задача 5

Найдите площадь квадрата со стороной 15 см.

Решение

Воспользуемся формулой площади квадрата через сторону.

S = a ^2 = 15 ^2 = 225 : см^2

Ответ: 225 см²

Проверка .

Источник

Как рассчитать площадь квадрата

На данной странице калькулятор поможет рассчитать площадь квадрата онлайн. Для расчета задайте длину стороны или диагональ.

Квадрат — это правильный четырёхугольник. У него все стороны и углы равны между собой. Квадрат есть частный вид прямоугольника, а также частный вид ромба.

Через сторону

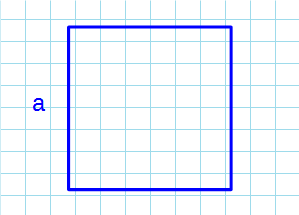
Формула для нахождения площади квадрата через сторону:

a — сторона квадрата.

Через диагональ

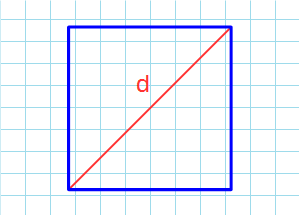
Формула для нахождения площади квадрата через диагональ:

d — диагональ квадрата.

Источник

Площадь квадрата можно найти с помощью двух основных формул:

1) Через сторону.

2) Через диагональ.

Как найти площадь квадрата, если известна его сторона.

Как известно, квадрат — это частный случай прямоугольника, у которого все стороны равны.

Площадь прямоугольника равна произведению 2 его сторон:

Sпр = a * b, a и b — стороны прямоугольника.

В случае с квадратом a = b.

Таким образом, площадь квадрата будет находиться по формуле:

Sкв = a².

Например, если сторона квадрата равна 10 см., то его площадь = 10 * 10 = 100 см².

Как найти площадь квадрата, если известна его диагональ.

Диагональ делит квадрат на 2 прямоугольных треугольника. При этом диагональ является гипотенузой, а стороны квадрата — катетами.

Нам нужно выразить квадрат стороны через теорему Пифагора. Согласно данной теореме:

a*a + b*b = c*c.

a и b — катеты, c — гипотенуза.

В нашем случае a = b, а гипотенуза — это диагональ d.

Перепишем формулу в виде:

2a² = d².

a² = d² / 2.

Таким образом, если известна диагональ квадрата, то его площадь равна половине квадрата этой диагонали.

Например, если диагональ равна 10 см., то площадь квадрата = 10 * 10 / 2 = 50 см².

Источник

Площадь квадрата, как посчитать площадь квадрата. Формула площади квадрата.

Формула площади квадрата.

Площадь квадрата обозначается буквой — S.

Сторона квадрата обозначается любой буквой, которая вам нравится, кроме занятой S.

Обычно сторону обозначают буквой — «a»

Формула площади квадрата : площадь квадрата равна стороне квадрата во второй степени.

Либо может встречаться вот такая формулировка площади квадрата:

Площадь квадрата равна произведению стороны квадрата на себя.

S = a²

Где S — площадь квадрата,

a — длина одной из сторон.

Пример подсчета площади квадрата

Как вычислить площадь квадрата?

Для того, чтобы найти площадь квадрата — нужно знать длину стороны квадрата.

Предположим, что у нас есть квадрат, площадь которого нам требуется узнать!

Пусть это будет 10см.

Условие задачи :

Сколько будет площадь квадрата со стороной 10см.

Решение задачи — найти площадь квадрата:

Как вы помните из правила высчитывания площади квадрата — нужно сторону квадрата умножить на себя или возвести во вторую степень.

S = a²

Умножаем сторону квадрата 10, на себя, на 10 :

10 * 10 = 100см²
Ответ :
Площадь квадрата со стороной 10см, будет равна 100см²
100см²

Как найти площадь квадрата если известен периметр!?

Условие задачи : найдите площадь квадрата, если известен периметр = 32см.

Решение задачи — найти площадь квадрата:

Для того, чтобы узнать площадь квадрата по его периметру нам понадобится формула подсчета периметра квадрата:

P = 4a

Далее нам нужно 32 разделить на 4, мы найдем длину одной стороны квадрата.

И далее по формуле площади квадрата узнаем его площадь :

S = a² = 4² = 16см²

Ответ задачи :

Квадрат, у которого периметр 32 см, площадь равна 16см²

Как найти площадь квадрата если известна диагональ!?

Условие задачи : найдите площадь квадрата, если известна диагональ квадрата = 8см.

Решение задачи — найти площадь квадрата:

Для того, чтобы найти диагональ квадрата, нам нужно вспомнить формулу пифагора :

a² + a² = d²

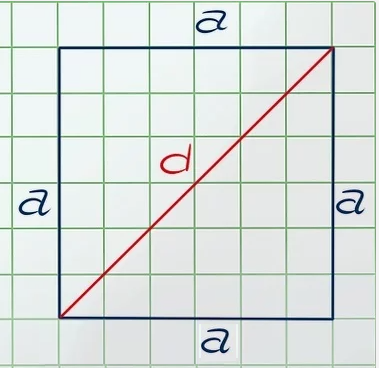
Немного нужно преобразовать :

a² + a² = d² -> 2a² = d² -> a² = d²/2

А если S = a², то S = d²/2

И далее нам нужно подставить нашу диагональ :

S = 8²/2 = 64/2 = 32см².

Ответ :

Если диагональ квадрата равна — 8см, То площадь квадрата равна — 32см².

Какая единица измерения площади квадрата!?

После того, как я написал страницу и началась выдача страницы, интересный поисковый вопрос : «площадь квадрата почему см2«.

Человек, видимо, хотел спросить, откуда двойка в единице измерения площади квадрата!?

Мы можем рассказать… о том, в какой единице измерения измеряются площадь квадрата и откуда там берется двойка!?

Единица измерения площади квадрата

Единица измерения площади квадрата — может быть, любая мера длины в квадрате.

Если мера длины сантиметр, то площадь будет сантиметр в квадрате — см².

Если мера длины метр, то площадь будет метр в квадрате — м².

Если мера длины километр, то площадь будет километр в квадрате — км². и т.д…

Почему единица измерения площади квадрата пишется с двойкой

Обычно в младших классах, на единицу измерения не обращают внимания. Но уже в старших классах на это обращают некоторое внимание!

Почему единица площади(и в том числе квадрата) обозначают двойкой чуть выше буквеного выражения!?

Если мы вспомним, что площадь квадрата равна умноженной длины стороны на себя и напишем единицу измерения… то мы увидим откуда берется двойка…

Давайте покажем на примере…

Пусть надо найти площадь квадрата со стороной 12 см.

Так и записываем в формулу :

S = 12см * 12см

Далее никуда единицу измерения не убираем, а умножаем их между собой, вот отсюда и получается квадратные сантиметры(или другая мера длины в квадрате) :

12*12(см*см) = 12²см² = 144см²

Как найти площадь квадрата зная радиус вписанной окружности!?

Задача :

Как найти площадь квадрата зная радиус вписанной окружности!?

Это очень простая задача!

Диаметр вписанной окружности равна стороне квадрата.

Диаметр окружности равен 2R.

Значит сторона квадрата равна 2R.

Далее вспоминаем формулу площади квадрата — S = a², где a — сторона квадрата, которая равна = 2R.

Значит площадь квадрата равна S = (2R)²

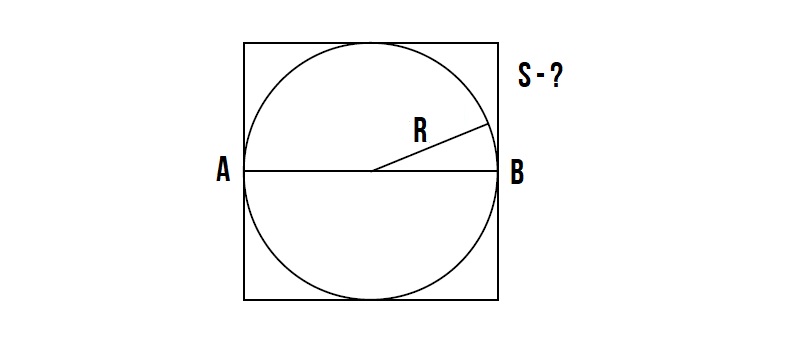
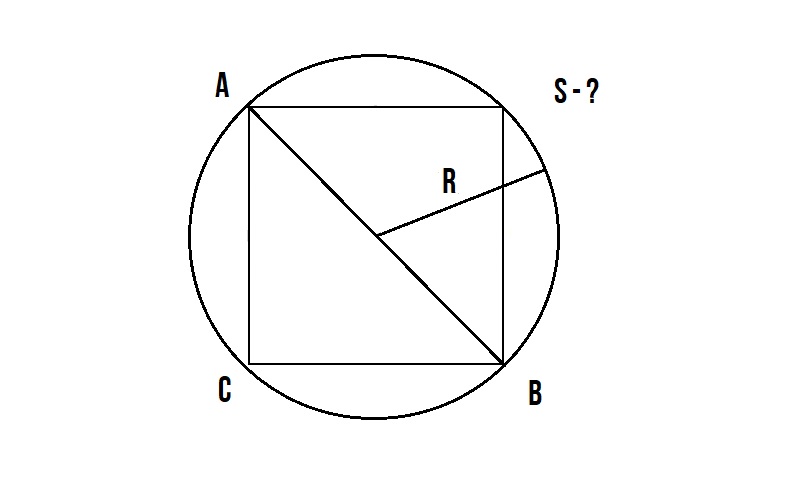
Как найти площадь квадрата зная радиус описанной окружности!?

Задача :

Как найти площадь квадрата зная радиус описанной окружности!?

Данная задача такая же простая, как и выше описанная!

У нас известен радиус окружности описанной вокруг квадрата.

Диаметр окружности AB равен диагонали квадрата AB и мы знаем, что диаметр окружности равен двум радиусам d = 2R.

По диагонали квадрата мы уже один раз высчитывали площадь здесь -> S = d²/2

Далее подставляем S = (2R)²/2

Найти площадь квадрата онлайн

Для того чтобы посчитать площадь квадрата онлайн, вам требуется в поле :

Сторона квадрата — заполнить значением стороны квадрата.

И нажать кнопку посчитать.

Источник