Эта информация доступна зарегистрированным пользователям
Величина- это свойство объекта, явления, процесса, которое характеризуются количественно.
Любая величина имеет свое значение.
Значение величины выражается некоторым числом (размером) с указанием единицы измерения.
Единицей измерения величины является некоторая мера, числовое значение, которой равно единице.
На этом уроке рассмотрим единицы измерения длины и площади.
Выясним область их применения.
Эта информация доступна зарегистрированным пользователям
Познакомимся с новыми единицами площади.
Узнаем, как связаны единицы площади между собой.
Разберем правила и способы измерения площадей.
Единицы, в которых измеряются величины, называются единицами измерения.
Одна и та же величина может быть выражена в разных единицах измерения.
Числовое значение величины непосредственно зависит от выбранной единицы измерения.
Вам уже хорошо известны такие единицы измерения длины, как:
1. Миллиметр— единица длины в системе СИ.
Русское обозначение: мм.
Международное обозначение: mm.
Наглядно представить миллиметр можно с помощью шкалы линейки.
Одному миллиметру равно расстояние между самыми маленькими делениями на линейке.
Эта информация доступна зарегистрированным пользователям
Миллиметры применяют в качестве стандартной единицы измерения длины практически во всех странах мира (единица длины в системе СИ).
Используют данную меру длины в тех случаях, когда необходима высокая точность измерений и вычислений.
На чертежах миллиметр является единицей измерения по умолчанию.
2. Сантиметр— единица длины в системе СИ.
Русское обозначение: см.
Международное обозначение: сm.
Наглядно представить сантиметр можно с помощью линейки: десять миллиметровых делений представляют собой один сантиметр.
Эта информация доступна зарегистрированным пользователям
Отрезок один сантиметр равен отрезку десять миллиметров.
1 см = 10 мм.
3. Дециметр— единица измерения длины в системе СИ.
Русское обозначение: дм.
Международное обозначение: dm.
Наглядно представить сантиметр можно на сантиметровой линейке как отрезок равный десяти сантиметрам.
Эта информация доступна зарегистрированным пользователям
В одном дециметре содержится десять сантиметров или сто миллиметров.
1 дм = 10 см = 100 мм.
На практике дециметр используется не часто.
4. Метр— мера длины, основная в системе СИ.
Русское обозначение: м.
Международное обозначение: m.
Отрезок в один метр равен отрезку десять дециметров.
1 м = 10 дм.
Каждые десять дециметров содержат по десять сантиметров, значит
1 м = 100 см.
С помощью обычной школьной линейки представить метр затруднительно.
Метр легко отмерить с помощью рулетки или портновской сантиметровой ленты.
Эта информация доступна зарегистрированным пользователям
5. Километр— широко используемая единица измерения длины, расстояния.
Русское обозначение: км.
Международное обозначение: km.
«Кило» от греческого тысяча, а «километр» — значит тысяча и метр.
В одном километре тысяча метров.
1 км = 1000 м.
Трудно наглядно изобразить километр, так как это большая мера длины.
В километрах измеряют обычно расстояния между населенными пунктами, странами, протяженность рек и морей, материков, островов и др.
Длина — это характеристика линейных размеров объекта.
Для вычисления площади необходимо знать эти линейные размеры.
Так для нахождения площади прямоугольника нужно знать длины его сторон.
Всем хорошо известно, что площадь прямоугольника равна произведению его длины и ширины.
Так как длина и ширина выражаются в линейных единицах, то их произведение будет представлять собой квадратную меру длины.
Эта информация доступна зарегистрированным пользователям
Таким образом, площадь измеряется в квадратных единицах измерения длины.
К основным единицам площади относят: квадратный километр, квадратный метр, квадратный дециметр, квадратный сантиметр, квадратный миллиметр.
Рассмотрим кратко каждую из них.
Вспомним, что квадрат- это прямоугольник, у которого все стороны равны.
Квадратная единица представляет собой единичный квадрат, у которого сторона равна единице измерения длины.
Площадь такого квадрата равна одной единице измерения длины во второй степени (т.е. возведенная в квадрат).
1. Квадратный миллиметр представляет собой квадрат со стороной в один миллиметр (1 мм).
Русское обозначение: мм2.
Международное обозначение: mm2.
Эта информация доступна зарегистрированным пользователям
S = 1 мм ∙ 1мм = 1 мм2.
Квадратный миллиметр используют для измерения площадей маленьких поверхностей.
В квадратных миллиметрах измеряют, например, чипы микропроцессоров, площадь сечения провода, проволоки и т.д.
Для начертания и измерения объектов небольшой площади удобно использовать миллиметровую бумагу.
Эта информация доступна зарегистрированным пользователям
2. Квадратный сантиметр— это площадь квадрата, сторона которого равна один сантиметр (1 см).
Русское обозначение: см2.
Международное обозначение: сm2.
Эта информация доступна зарегистрированным пользователям
S = 1 см ∙ 1см = 1 см2.
Квадратный сантиметр довольно часто применяют как единицу измерения площади фигур в школьной программе, так как квадратные сантиметры позволяют выражать небольшие по значению площади, соизмеримые с листом бумаги.
Легко представить и приближенно изобразить квадратный сантиметр на тетрадном листе в клетку: 2 клетки ≈ 1 см, поэтому квадрат, состоящий из четырех клеток, будет изображать 1 см2.
Эта информация доступна зарегистрированным пользователям
3. Квадратный дециметр— это площадь квадрата, сторона которого равна один дециметр (1 дм).
Русское обозначение: дм2.
Международное обозначение: dm2.
Эта информация доступна зарегистрированным пользователям
S = 1 дм ∙ 1 дм = 1 дм2.
На практике квадратный дециметр не используют, практически не используют его и в быту.
Квадратный дециметр можно встретить при решении некоторых математических задач, он существует как промежуточная единица между квадратным сантиметром и квадратным метром.
Дециметр квадратный можно приблизительно изобразить на тетрадном листе.
2 клетки ≈ 1 см.
10 см = 1 дм.
20 клеток ≈ 1 дм.
Следовательно, квадрат со стороной 20 тетрадных клеток будет изображать 1 дм2.
4. Квадратный метр— это площадь квадрата со стороной один метр (1 м).
Русское обозначение: м2.
Международное обозначение: m2.
Эта информация доступна зарегистрированным пользователям
S = 1 м ∙ 1 м = 1 м2.
Квадратный метр- это основная и самая распространенная единица площади в Международной системе СИ.
Часто используется для оценки площадей зданий и различных помещений (жилых, офисных, производственных), применяют в сельском хозяйстве, науке и технике, архитектуре, строительстве, в разных областях знаний: физике, медицине, географии и т.д.
Практически ни один ремонт не обходится без вычисления площади, причем эту площадь чаще всего приходится вычислять в метрах квадратных.
Эта информация доступна зарегистрированным пользователям
Необходимо знать и уметь высчитывать площадь стен, пола, потолка, окон и т.д. при закупке строительных материалов.
Наглядно представить один метр квадратный можно, вырезав из обоев квадрат со стороной в один метр.
5. Квадратный километр— площадь квадрата со стороной один километр (1 км).
Русское обозначение: км2.
Международное обозначение: km2.
Эта информация доступна зарегистрированным пользователям
S = 1 км ∙ 1 км = 1 км2.
Для измерения больших площадей используют квадратный километр.
В квадратных километрах измеряют площади крупных объектов: городов, стран, континентов, озер, морей, океанов, планет и т.д.
Эта информация доступна зарегистрированным пользователям
Кроме основных единиц измерения площадей существуют единицы для измерения площадей земельных участков.
К таким единицам относятся Гектар и Ар.
Ар— это внесистемная единица площади, равная 100 квадратным метрам, т.е. это квадрат со стороной в 10 м.
Ар от латинского «area»- площадь, поверхность.
Обозначение: а.
Эта информация доступна зарегистрированным пользователям
S = 10 м ∙ 10 м = 100 м2 = а.
Ар в некоторых странах называют иначе.
В России ар имеет второе название (разговорное)- «сотка» (так как ар равен сотне квадратных метров).
Пример.
2 сотки- это 2 ар.
9 соток- это 9 ар и т.д.
Используют данную единицу площади в сельском и лесном хозяйстве для измерения небольших земельных и лесных участков.
Гектар— единица измерения площади, равная площади квадрата со стороной 100 м.
Русское обозначение: га.
Международное обозначение: ha.
Такое обозначение было принято Международным комитетом мер и весов в 1879 году.
На сегодняшний день гектар допущен в качестве единицы измерения площади вместе с единицами измерения системы СИ.
Гектар от латинского «гекто» и «ар» означает «сто» и «ар» соответственно.
Эта информация доступна зарегистрированным пользователям
S = 100 м ∙ 100 м = 10000 м2 = га.
1 га = 100 ар = 100 соток.
Используют для обозначения площади больших участков земли: сельскохозяйственных угодий, лесов, полей.
До введения гектара в России использовали другие меры площади, например, десятина (примерно равная гектару).
Эта информация доступна зарегистрированным пользователям
Единицы измерения площади можно переводить из одной единицы в другую.
Например, чтобы найти сколько в квадратном сантиметре (1 см2) содержится квадратных миллиметров, необходимо вспомнить, сколько в одном сантиметре (1 см) миллиметров.
Известно, что 1 см2— это квадрат со стороной в 1 см.
1 см = 10 мм.
Тогда все четыре стороны имеют длину равную 10 мм.
Вычислим площадь квадрата со стороной 10 мм, для этого умножим длину квадрата (равную 10 мм) на его ширину (равную 10 мм), т.е. возведем число 10 в квадрат.
S = 10 мм ∙ 10 мм = 102 мм2 = 100 мм2.
Эта информация доступна зарегистрированным пользователям
Получаем: на один квадратный сантиметр приходится сто квадратных миллиметров.
1 см2 = 100 мм2
В таком случае, чтобы перевести квадратные сантиметры в квадратные миллиметры, необходимо количество квадратных сантиметров умножить на 100.
Пример 1.
Переведем 4 см2 в квадратные миллиметры.
Так как 1 см2— это 100 мм2, то число квадратных миллиметров в 100 раз больше, чем число квадратных сантиметров, следовательно, умножим 4 см2 на 100.
Решение:
4 см2 = 4 ∙ 100 = 400 мм2.
Ответ: 4 см2 = 400 мм2.
Соответственно, чтобы перевести квадратные миллиметры в квадратные сантиметры, нужно количество квадратных миллиметров разделить на 100.
Пример 2.
Выразим 400 мм2 в квадратных сантиметрах.
Так как 100 мм2— это 1 см2, выясним сколько будет содержаться квадратных сантиметров (1 см2 = 100 мм2) в 400 мм2.
Разделим 400 мм2 на 100.
Решение:
400 мм2 = 400 ÷ 100 = 4 см2.
Ответ: 400 мм2 = 4 см2.
Рассуждая по такому принципу, можно установить взаимосвязь других единиц измерения площади.
Для этого необходимо четко знать и помнить соотношения единиц измерения длины.
1 см = 10 мм
1 дм = 10 см = 100 мм
1 м = 10 дм = 100 см = 1000 мм
1 км = 1000 м
Запишем соотношение единиц площади:
Эта информация доступна зарегистрированным пользователям
Пример 3.
Площадь лесного участка составляет 40 га.
Выразим данную площадь в м2.
Решение:
1 га- это квадрат площадью 10000 м2, значит 40 га- это 40 квадратов каждый площадью 10000 м2, а это значит:
40 га = 40 ∙ 10000 = 400000 м2.
Ответ: 40 га = 400000 м2.
Пример 4.
Площадь распаханного поля составляет 5 ар.
Выразим данную площадь поля в м2.
Решение:
1 ар- это квадрат площадью 100 м2, значит, 5 ар- это 5 квадратов площадью 100 м2 каждый, а это значит:
5 а = 5 ∙ 100 = 500 м2.
Ответ: 5 а = 500 м2.
Иначе можно сказать так: площадь распаханного поля составляет 5 соток.
Пример 5.
Выразим 2 м2 14 см2 в квадратных сантиметрах.
Решение:
Так как 1 м2 = 10000 см2, то 2 м2 = 20000 см2.
20000 см2 да еще 14 см2 получаем:
2 м2 14 см2 = 20000 см2 + 14 см2 = 20014 см2
Ответ: 2 м2 14 см2 = 20014 см2
Пример 6.
На рисунке изображен прямоугольник ABCD со сторонами 16 см и 2 м 20 см.
Эта информация доступна зарегистрированным пользователям
Найдем площадь прямоугольника ABCD.
Если стороны прямоугольника выражены в разных единицах измерения, то для вычисления площади необходимо длины сторон этого прямоугольника перевести в одинаковые единицы измерения.
Переведем длину и ширину прямоугольника ABCD в сантиметры.
Ширина прямоугольника а = 16 см уже выражена в сантиметрах.
Длину прямоугольника b = 2 м 20 см выразим в сантиметрах.
Так как 1 м = 100 см, то 2 м = 200 см.
200 см да еще 20 см получаем:
b = 200 см + 20 см = 220 см
Эта информация доступна зарегистрированным пользователям
Умение измерять и высчитывать площадь различных объектов- очень ценное знание, которое используется во многих сферах нашей жизни.
Например, часто приходится давать оценку земельных участков различного назначения.
В таком случае площадь может быть определена по результатам обмера участка в реальности, а также по планам и картам.
Эта информация доступна зарегистрированным пользователям
Для того чтобы измерить площадь помещения, нет необходимости совершать сложные вычислительные операции и иметь специальные измерительные приборы.
Измерение площади в таком случае сводится к измерению рулеткой длины отрезков, ограничивающих эту площадь.
Чаще всего помещение имеет прямоугольную или квадратную форму, вычислить площадь такой фигуры несложно.
Необходимо измерить длину и ширину помещения (в одинаковых единицах измерения) и перемножить полученные значения.
Эта информация доступна зарегистрированным пользователям
Для расчета применяется формула: S = а ∙ b
S— площадь помещения
а— ширина помещения
b— длина помещения
Если же необходимо определить площадь сложной формы, то измерением просто длины и ширины помещения не обойтись.
Известно, что общая площадь фигуры равна сумме площадей ее частей.
S = S1 + S2 + S3…
В таком случае необходимо измеряемое пространство разделить условно на прямоугольники и квадраты.
Определить площади каждой простой фигуры, затем сложить получившиеся значения площадей.
Рассмотрим пример.
Найдем площадь всей квартиры, изображенной на рисунке-плане.
Эта информация доступна зарегистрированным пользователям
Условно разобьем пространство всей квартиры на прямоугольники, у каждого найдем площадь.
S1 = а1 ∙ b1— площадь кухни в м2
S2 = а2 ∙ b2— площадь спальни в м2
S3 = а3 ∙ b3— площадь гостиной в м2
S4 = а4 ∙ b4— площадь прихожей в м2
S5 = а5 ∙ b5— площадь ванной комнаты в м2.
S— общая площадь квартиры, ее найдем, сложив площади каждой комнаты
S= S1 + S2 + S3 + S4 + S5
Рассмотрим решение нескольких практических задач.
Задача №1.
Определите сколько стоит жалюзи на окно шириной 2 м и высотой 2 м, если цена жалюзи 600 рублей за 1 м2.
Эта информация доступна зарегистрированным пользователям
Пусть а— ширина окна, b— длина окна, р— цена жалюзи за 1 м2.
Эта информация доступна зарегистрированным пользователям
Задача №2.
Эта информация доступна зарегистрированным пользователям
Линолеум стоит 300 рублей за 1 м2.
Определите стоимость линолеума, который необходимо купить, чтобы застелить пол в комнате шириной 4 м и длинной 6 м.
Пусть а— ширина комнаты, b— длина комнаты, р— цена линолеума за 1 м2.
Эта информация доступна зарегистрированным пользователям
Задача №3
Эта информация доступна зарегистрированным пользователям
Сколько банок краски потребуется для покраски стены длинной 4 м шириной 3 м, если на 1 м2 требуется 250 г краски.
Краска продается в банках по 3000 г.
Выясним, какую площадь необходимо покрасить и сколько на это понадобится граммов краски.
Разделим общее количество необходимой краски на массу одной банки, получим число банок, которые нужно купить для покраски стены.
Пусть m— масса краски, которая расходуется на 1 м2
mб— масса одной банки с краской
mс— масса краски, которая необходима для покраски всей стены
n— число банок с краской, которые нужно купить для покраски стены
Эта информация доступна зарегистрированным пользователям
Если бы в стене был оконный или дверной проем, то необходимо было бы высчитать площадь окна (двери) и вычесть это значение из общей площади стены, которая подлежит покраске.
Эта информация доступна зарегистрированным пользователям
Читайте также
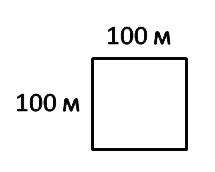
Как рассчитать площадь квадрата
На данной странице калькулятор поможет рассчитать площадь квадрата онлайн. Для расчета задайте длину стороны или диагональ.
Квадрат — это правильный четырёхугольник. У него все стороны и углы равны между собой. Квадрат есть частный вид прямоугольника, а также частный вид ромба.
Через сторону
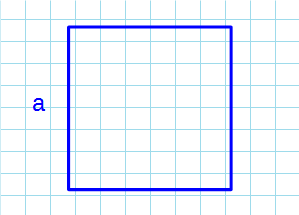
Формула для нахождения площади квадрата через сторону:
a — сторона квадрата.
Через диагональ
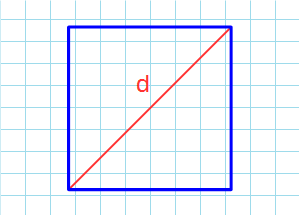
Формула для нахождения площади квадрата через диагональ:
d — диагональ квадрата.
Что такое квадрат и понятие его площади
Квадрат — простейшая плоская геометрическая фигура. Является одновременно правильным четырёхугольником и прямоугольником, все стороны которого равны.
Состоит соответственно из четырёх равных сторон, четырёх вершин ABCD и прямых углов 90°.
Под площадью квадрата подразумевается пространство, ограниченное его сторонами (та часть плоскости, что внутри). Способов расчёта существует немного, а формулы для вычисления площади весьма простые.
Как найти площадь квадрата через сторону
Данный способ и калькулятор позволит найти площадь квадрата через значение длины его сторон — введите его в соответствующее поле. В зелёном поле автоматически выведется результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через периметр
Данный способ и калькулятор позволит найти площадь квадрата через значение его периметра — введите его в соответствующее поле. В зелёном поле выведется результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через диагональ
Данный способ и калькулятор позволит найти площадь квадрата через значение длины его диагонали — введите его в соответствующее поле. В зелёном поле получите результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через радиус вписанной окружности
Данный способ и калькулятор позволит найти площадь квадрата через значение радиуса вписанной окружности — введите его в соответствующее поле. В зелёном поле выведется результат.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Как найти площадь квадрата через радиус описанной окружности
Данный способ и калькулятор позволит найти площадь квадрата через значение радиуса описанной окружности — введите его в соответствующее поле. В зелёном поле выведется результат автоматически.
Важно: если ваши единицы измерения — миллиметры, тогда площадь будет выражаться в мм²; если сантиметры — тогда в см² и так далее …
Ваша оценка?
[Оценок: 5 / Средняя: 4.6]
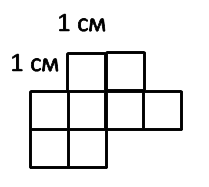
Рассмотрим фигуру ниже:
Вся фигура состоит из 8 квадратов со стороной 1 см каждый.
Площадь одного такого квадрата называют квадратным сантиметром и записывают:
1 см2.
Площадь всей фигуры 8 см2.
Запомните!
Площадь измеряется только в квадратных единицах длины. Всегда проверяйте свои ответы.
В математике для нахождения площади геометрических фигур используют специальные формулы,
в которых площадь обозначается заглавной латинской буквой «S».
Напоминаем, что площадь квадрата можно найти, умножив длину его стороны на саму себя.
Единицей площади служит площадь единичного квадрата. Например, если длина стороны квадрата,
равна 1 м, то его площадь равна 1
квадратному метру (1 м2); если длина
его стороны равна 1 см, то его площадь
равна 1 квадратному сантиметру
(1 см2).
Для нахождения площади какой-либо фигуры её сравнивают с единичным квадратом.
Как перевести квадратные единицы
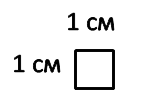
Рассмотрим квадрат со стороной 1 см.
Его площадь равна:
S = 1 см · 1 см = 1см2
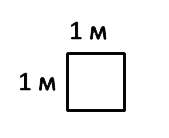
Рассмотрим квадрат со стороной 1 м.
Его площадь равна:
S = 1 м · 1 м = 1 м2
Известно, что: 1 м = 100 см
1 м2 = 1 м · 1 м = 100 см · 100 см = 10 000 см2
Увеличим сторону квадрата равную 1 м в
10 раз. Получим квадрат со
стороной 10 м.
Площадь такого квадрата называют ар или сотка.
S = 10 м · 10 м = 100 м2
В одном аре — сто квадратных метров.
Слово «сотка» часто используют в дачном хозяйстве, хотя это тоже самое, что и «ар».
1 ар (сотка) = 100 м2
Чтобы выразить ар в cм2, вспомним, что 1 м2 = 10 000 см2.
Значит: 1 ар (сотка) = 100 м2 = 100 · 10 000 см2 = 1 000 000 см2
Увеличим сторону квадрата равную 10 м в 10 раз.
Получим квадрат со
стороной 100 м.
Площадь такого квадрата называют гектар. Сокращенно «га». Но при произношении вслух наименование
проговаривается полностью.
Выразим гектар в квадратных метрах.
1 га = 100 м · 100 м = 10 000 м2
Теперь определим, сколько в одном гектаре аров.
1 ар = 100 м2
Значит: 10 000 м2 : 100 м2 = 100 (ар)
1 га = 100 ар
Для измерения больших площадей, например, территорий государств, материков используют квадратный километр.
То есть квадрат со стороной 1 км и
площадью 1 км2.
1 км = 1000 м
1 км2 = 1 км · 1 км = 1 000 м · 1 000 м = 1 000 000 м2
Для простоты расчётов предлагаем вам в помощь таблицу переводов квадратных единиц.
Таблица переводов квадратных единиц
Данная таблица поможет перевести гектары в кв. метры, гектары в ары и наоборот.
| га | ар | м2 | cм2 | |
|---|---|---|---|---|
| 1 км2 | 100 га | 10 000 ар | 1 000 000 м2 | 1 000 000 000 cм2 |
| 1 га | 1 га | 100 ар | 10 000 м2 | 100 000 000 cм2 |
| 1 ар | 0,01 га | 1 ар | 100 м2 | 1 000 000cм2 |
| 1 м2 | 0,000 1 га | 0,01 ар | 1 м2 | 10 000 cм2 |
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
12 сентября 2018 в 20:57
Дмитрий Мозговой
Профиль
Благодарили: 0
Сообщений: 1
Дмитрий Мозговой
Профиль
Благодарили: 0
Сообщений: 1
Внутри большего квадрата расположен меньший квадрат площади 73. Известно, что длины отрезков, на которые сторона большего квадрата делится вершинами меньшего квадрата, — натуральные числа. Чему равна площадь большего квадрата?
0
Спасибо
Ответить
14 октября 2018 в 20:45
Ответ для Дмитрий Мозговой
Дарья Тихая
Профиль
Благодарили: 0
Сообщений: 1
Дарья Тихая
Профиль
Благодарили: 0
Сообщений: 1
146
0
Спасибо
Ответить
21 октября 2018 в 15:44
Ответ для Дмитрий Мозговой
Владимир Шварцман
Профиль
Благодарили: 0
Сообщений: 1
Владимир Шварцман
Профиль
Благодарили: 0
Сообщений: 1
Пусть отрезки большего квадрата a и в. Тогда а2 + в2 =73 Сумма двух чисел нечётна если одно чёт., а второе нечёт. Это 1,9,25,49 и 4, 16,36.64 Легко видеть, что это числа 9 и 64.Т.е. а=3 и в=8 Пл. большого квадрата=112 =121
0
Спасибо
Ответить
12 ноября 2018 в 3:31
Ответ для Дмитрий Мозговой
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Неверно.
0
Спасибо
Ответить
22 июня 2016 в 20:17
Клара Чукаева
Профиль
Благодарили: 0
Сообщений: 1
Клара Чукаева
Профиль
Благодарили: 0
Сообщений: 1
д вечер. у меня вопрос: как найти площадь таблички размером 50 см на 75 см? если перемножить, как нам предлагает школьная программа, то получается 3750 см2, разве это возможно? я ошибаюсь? напишите формулу для расчета пожалуйста?
0
Спасибо
Ответить
24 июня 2016 в 12:18
Ответ для Клара Чукаева
Павел Асафов
Профиль
Благодарили: 0
Сообщений: 2
Павел Асафов
Профиль
Благодарили: 0
Сообщений: 2
Здравствуйте! Все верно.
Формула площади прямоугольника S=a · b
(a)50 · (b)75=3750 см2
Может вы спутали с периметром? Периметр будет равен 250 см
a ·2+b · 2
0
Спасибо
Ответить
16 января 2016 в 18:29
Надюша Бисерова
Профиль
Благодарили: 0
Сообщений: 1
Надюша Бисерова
Профиль
Благодарили: 0
Сообщений: 1
ширина прамоугольника 23 см. на сколько увеличиться площадь прамоугольника, если его длину увеличить на 3 см?
подскажите решение пожалуйста
0
Спасибо
Ответить
21 января 2016 в 16:17
Ответ для Надюша Бисерова
Сергей Фадеев
Профиль
Благодарили: 0
Сообщений: 6
Сергей Фадеев
Профиль
Благодарили: 0
Сообщений: 6
на 3 см квадратных
если я не ошибаюсь взависимости от длины
0
Спасибо
Ответить
24 января 2016 в 13:50
Ответ для Надюша Бисерова
Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
Инна Шабрашина
Профиль
Благодарили: 0
Сообщений: 5
увеличится на 69
0
Спасибо
Ответить
12 октября 2015 в 17:22
Мося Мося
Профиль
Благодарили: 0
Сообщений: 1
Мося Мося
Профиль
Благодарили: 0
Сообщений: 1
найди площадь квадрата периметр которого 280см
0
Спасибо
Ответить
1 июля 2016 в 14:20
Ответ для Мося Мося
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Для нахождения площади квадрата в данном случае нам понадобятся две формулу, а именно:
1) Формула периметра квадрата P=4a. Подробно про периметр читаем здесь http://math-prosto.ru/?page=pages/perimeter/perimeter.php
2) Формула площади квадрата S=a2. Подробно читать здесь http://math-prosto.ru/?page=pages/area/area_figures.php
Приступим к решению. Выразим сторону квадрата из формулы периметра:
P=4a
a=P: 4
a= 280: 4 = 70 (см)
Теперь воспользуемся формулой площади квадрата:
S=a2
S=702=4900 (см2)
Ответ: площадь квадрата равна 4900 см2
0
Спасибо
Ответить
4 сентября 2015 в 15:44
Игорь Винников
Профиль
Благодарили: 0
Сообщений: 2
Игорь Винников
Профиль
Благодарили: 0
Сообщений: 2
Площадь прямоугольника64мс2, одна из сторон 16см. Надо найти соседнюю сторону
0
Спасибо
Ответить
1 сентября 2016 в 10:18
Ответ для Игорь Винников
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Площадь прямоугольника рассчитывается по формуле S=a · b. Подставим значения в формулу и вычислим вторую сторону:
64=16 · b
b=64/16=4
вторая сторона равна 4.
проверка: 16 · 4 = 64.
Ответ: Соседняя сторона прямоугольника равна 4 см.
0
Спасибо
Ответить
6 июля 2015 в 17:48
Дмитрий Рыжков
Профиль
Благодарили: 0
Сообщений: 2
Дмитрий Рыжков
Профиль
Благодарили: 0
Сообщений: 2
Посмотрите, у вас не первый раз перепутаны буквы в примерах.Например посмотрите нм тему: площадь сложных фигур.там же треугольник обозначен одними буквами, а написано в примере другими совершенно. Никто не ответил по предыдущей теме.спасибо.
0
Спасибо
Ответить
12 июля 2015 в 13:31
Ответ для Дмитрий Рыжков
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
Здравствуйте, Дмитрий.
Благодарим Вас за указанное замечание.
Пожалуйста, укажите, более конкретно место ошибки.
В уроке «Площадь сложных фигур» мы не нашли ошибку, о которой Вы написали.
0
Спасибо
Ответить
17 мая 2015 в 10:59
Соня Кизилова
Профиль
Благодарили: 0
Сообщений: 1
Соня Кизилова
Профиль
Благодарили: 0
Сообщений: 1
Самостоятельная работа.
Задание 3.
На сколько частей разбивают плоскость 4 прямые, пересекающиеся в одное точке?
Задание 2.
Начертите угол MON. Отметьте точку K, лежащую внутри этого угла, и точку L, лежащую на отрезке NK.
Задание 4.
Постройте треугольник ABC со стороной AB= 6см,?ABC= 45градусов, ?BAC= 75 градусов.Помогите пожалуйста…
0
Спасибо
Ответить
17 мая 2015 в 12:57
Ответ для Соня Кизилова
Ярослава Фесенко
Профиль
Благодарили: 0
Сообщений: 3
Ярослава Фесенко
Профиль
Благодарили: 0
Сообщений: 3
1.8 частей
0
Спасибо
Ответить

{S = a ^2}
На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.
Квадрат — четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.
Содержание:
- калькулятор площади квадрата
- формула площади квадрата через сторону
- формула площади квадрата через диагональ
- формула площади квадрата через радиус вписанной окружности
- формула площади квадрата через радиус описанной окружности
- формула площади квадрата через периметр
- примеры задач
Формула площади квадрата через сторону
S = a ^2
a — сторона квадрата
Формула площади квадрата через диагональ
S=dfrac{d^2}{2}
d — диагональ квадрата
Формула площади квадрата через радиус вписанной окружности
S = 4r^2
r — радиус вписанной окружности
Формула площади квадрата через радиус описанной окружности
S = 2R^2
R — радиус описанной окружности
Формула площади квадрата через периметр
S = dfrac{P^2}{16}
P — периметр квадрата
Примеры задач на нахождение площади квадрата
Задача 1
Найдите площадь квадрата если его диагональ равна 1.
Решение
Для решения задачи воспользуемся формулой.
S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2
Ответ: 0.5 см²
Проверим ответ на калькуляторе .
Задача 2
Найдите площадь квадрата, описанного вокруг окружности радиуса 83.
Решение
Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.
S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2
Ответ: 13778 см²
Проверим ответ с помощью калькулятора .
Задача 3
Найдите площадь квадрата если его сторона равна 8 см.
Решение
Используем первую формулу.
S = a ^2 = 8 ^2 = 64 : см^2
Ответ: 64 см²
Проверим результат на калькуляторе .
Задача 4
Найдите площадь квадрата периметр которого равен 456 см.
Решение
Используем формулу для площади квадрата через периметр.
S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2
Ответ: 12996 см²
Проверка .
Задача 5
Найдите площадь квадрата со стороной 15 см.
Решение
Воспользуемся формулой площади квадрата через сторону.
S = a ^2 = 15 ^2 = 225 : см^2
Ответ: 225 см²
Проверка .