Как найти площадь квадрата зная корень - Исправление недочетов и поиск решений вместе с Examum.ru

{S = a ^2}

На этой странице вы найдете удобный калькулятор для расчета площади квадрата и формулы, которые помогут найти площадь квадрата через его сторону, диагональ, периметр, а также радиусы вписанной и описанной окружности.

Квадрат — четырёхугольник, у которого все углы прямые (90 градусов) и все стороны равны между собой. Из-за своих свойств квадрат часто называют правильным четырехугольником.

Содержание:

калькулятор площади квадрата
формула площади квадрата через сторону
формула площади квадрата через диагональ
формула площади квадрата через радиус вписанной окружности
формула площади квадрата через радиус описанной окружности
формула площади квадрата через периметр
примеры задач

Формула площади квадрата через сторону

S = a ^2

a — сторона квадрата

Формула площади квадрата через диагональ

S=dfrac{d^2}{2}

d — диагональ квадрата

Формула площади квадрата через радиус вписанной окружности

S = 4r^2

r — радиус вписанной окружности

Формула площади квадрата через радиус описанной окружности

S = 2R^2

R — радиус описанной окружности

Формула площади квадрата через периметр

S = dfrac{P^2}{16}

P — периметр квадрата

Примеры задач на нахождение площади квадрата

Задача 1

Найдите площадь квадрата если его диагональ равна 1.

Решение

Для решения задачи воспользуемся формулой.

S = dfrac{d^2}{2} = dfrac{1^2}{2} = dfrac{1}{2} = 0.5 : см^2

Ответ: 0.5 см²

Проверим ответ на калькуляторе .

Задача 2

Найдите площадь квадрата, описанного вокруг окружности радиуса 83.

Решение

Для решения этой задачи используем формулу площади квадрата через радиус описанной окружности.

S = 2R^2 = 2 cdot 83^2 = 2 cdot 6889 = 13778 : см^2

Ответ: 13778 см²

Проверим ответ с помощью калькулятора .

Задача 3

Найдите площадь квадрата если его сторона равна 8 см.

Решение

Используем первую формулу.

S = a ^2 = 8 ^2 = 64 : см^2

Ответ: 64 см²

Проверим результат на калькуляторе .

Задача 4

Найдите площадь квадрата периметр которого равен 456 см.

Решение

Используем формулу для площади квадрата через периметр.

S = dfrac{P^2}{16} = dfrac{456^2}{16} = dfrac{456 cdot cancel{456}^{ : 57}}{cancel{16}^{ : 2}} = dfrac{57 cdot cancel{456}^{ : 228}}{cancel{2}^{ : 1}} = 57 cdot 228 = 12996 : см^2

Ответ: 12996 см²

Проверка .

Задача 5

Найдите площадь квадрата со стороной 15 см.

Решение

Воспользуемся формулой площади квадрата через сторону.

S = a ^2 = 15 ^2 = 225 : см^2

Ответ: 225 см²

Проверка .

Источник

Зная площадь квадрата, легко найти его сторону. Для этого из заданного значения площади необходимо извлечь квадратный корень.
S=a^2
a=√S

Периметр квадрата получится равным четырем таким корням.
P=4a=4√S

Для того чтобы найти диагональ квадрата, зная площадь, необходимо так же подставить вместо стороны полученное выражение.
d=√2 a=√2S

Углы пересечения диагоналей со сторонами и друг с другом останутся неизменными. (рис. 69.1)
m(

Радиус вписанной в квадрат окружности через площадь квадрата можно найти, подставив в формулу вместо стороны квадратный корень из площади.
r=a/2=√S/2

Для того чтобы найти радиус описанной окружности через площадь квадрата, нужно разделить сторону не на два, а на корень из двух. Тем самым, корни объединятся, и получится, что радиус равен корню из половины площади.
R=a/√2=√S/√2=√(S/2)

Источник

Квадрат – это правильный четырехугольник, в котором все углы и стороны равны между собой.

Довольно часто эту фигуру рассматривают, как частный случай ромба или прямоугольника. Диагонали квадрата равны между собой и используются в формуле площади квадрата через диагональ.
Для расчета площади рассмотрим формулу площади квадрата через диагонали:

$S={d^2}/2$

То есть площадь квадрата равна квадрату длины диагонали поделенному на два. Учитывая, что стороны фигуры равны, можно рассчитать длину диагонали из формулы площади прямоугольного треугольника или по теореме Пифагора.

Рассмотрим пример расчета площади квадрата через диагональ. Пусть дан квадрат с диагональю d = 3 см. Необходимо вычислить его площадь:
$S={3^2}/2=9/2=4,5 {cm}^2$
По этому примеру расчета площади квадрата через диагонали мы получили результат 4,5 ${cm}^2$ .

Площадь квадрата через сторону

Найти площадь правильного четырехугольника можно и по его стороне. Формула площади квадрата очень проста:

Так как в предыдущем примере расчета площади квадрата мы рассчитали значение по диаметру, теперь попробуем найти длину стороны:
Подставим значение в выражение:
Длина стороны квадрата будет равна 2,1 cm.

Очень просто можно использовать формулу площади квадрата вписанного в окружность.

Диаметр описанной окружности будет равен диаметру квадрата. Так как квадрат считается правильным ромбом, можно использовать формулу расчета площади ромба. Она равна половине произведения его диагоналей. Диагонали квадрата равны, значит формула будет выглядеть так: $S={d^2}/2$
Рассмотрим пример расчета площади квадрата вписанного в окружность.

Дан квадрат, вписанный в окружность. Диагональ окружности равна d= 6 см. Найдите площадь квадрата.
Мы помним, что диагональ окружности равна диагонали квадрата. Подставляем значение в формулу расчета площади квадрата через его диагонали:
$S={6^2}/2=36/2=18 cm^2$
Площадь квадрата равна 18 ${cm}^2$

Площадь квадрата через периметр

В некоторых задачах по условиям дается периметр квадрата и требуется расчет его площади. Формула площади квадрата через периметр выводится из значения периметра. Периметр – это сумма длин всех сторон фигуры. Т.к. в квадрате 4 равных стороны, то он будет равен P=4a Отсюда находим сторону фигуры a=P/4 Площадь квадрата по обычной формуле считается так: S=a^2 .
Рассмотрим пример расчета площади квадрата через периметр.

Дан квадрат с периметром P = 16 см. Найдите его площадь.
Находим сторону:

Теперь рассчитаем площадь:

Площадь данного квадрата равна 16 cm^2 .

Источник

Площадь квадрата, как посчитать площадь квадрата. Формула площади квадрата.

Формула площади квадрата.

Площадь квадрата обозначается буквой — S.

Сторона квадрата обозначается любой буквой, которая вам нравится, кроме занятой S.

Обычно сторону обозначают буквой — «a»

Формула площади квадрата : площадь квадрата равна стороне квадрата во второй степени.

Либо может встречаться вот такая формулировка площади квадрата:

Площадь квадрата равна произведению стороны квадрата на себя.

S = a²

Где S — площадь квадрата,

a — длина одной из сторон.

Пример подсчета площади квадрата

Как вычислить площадь квадрата?

Для того, чтобы найти площадь квадрата — нужно знать длину стороны квадрата.

Предположим, что у нас есть квадрат, площадь которого нам требуется узнать!

Пусть это будет 10см.

Условие задачи :

Сколько будет площадь квадрата со стороной 10см.

Решение задачи — найти площадь квадрата:

Как вы помните из правила высчитывания площади квадрата — нужно сторону квадрата умножить на себя или возвести во вторую степень.

S = a²

Умножаем сторону квадрата 10, на себя, на 10 :

10 * 10 = 100см²
Ответ :
Площадь квадрата со стороной 10см, будет равна 100см²
100см²

Как найти площадь квадрата если известен периметр!?

Условие задачи : найдите площадь квадрата, если известен периметр = 32см.

Решение задачи — найти площадь квадрата:

Для того, чтобы узнать площадь квадрата по его периметру нам понадобится формула подсчета периметра квадрата:

P = 4a

Далее нам нужно 32 разделить на 4, мы найдем длину одной стороны квадрата.

И далее по формуле площади квадрата узнаем его площадь :

S = a² = 4² = 16см²

Ответ задачи :

Квадрат, у которого периметр 32 см, площадь равна 16см²

Как найти площадь квадрата если известна диагональ!?

Условие задачи : найдите площадь квадрата, если известна диагональ квадрата = 8см.

Решение задачи — найти площадь квадрата:

Для того, чтобы найти диагональ квадрата, нам нужно вспомнить формулу пифагора :

a² + a² = d²

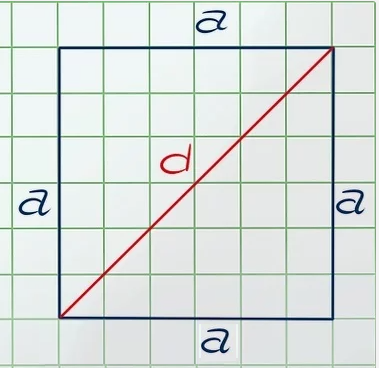
Немного нужно преобразовать :

a² + a² = d² -> 2a² = d² -> a² = d²/2

А если S = a², то S = d²/2

И далее нам нужно подставить нашу диагональ :

S = 8²/2 = 64/2 = 32см².

Ответ :

Если диагональ квадрата равна — 8см, То площадь квадрата равна — 32см².

Какая единица измерения площади квадрата!?

После того, как я написал страницу и началась выдача страницы, интересный поисковый вопрос : «площадь квадрата почему см2«.

Человек, видимо, хотел спросить, откуда двойка в единице измерения площади квадрата!?

Мы можем рассказать… о том, в какой единице измерения измеряются площадь квадрата и откуда там берется двойка!?

Единица измерения площади квадрата

Единица измерения площади квадрата — может быть, любая мера длины в квадрате.

Если мера длины сантиметр, то площадь будет сантиметр в квадрате — см².

Если мера длины метр, то площадь будет метр в квадрате — м².

Если мера длины километр, то площадь будет километр в квадрате — км². и т.д…

Почему единица измерения площади квадрата пишется с двойкой

Обычно в младших классах, на единицу измерения не обращают внимания. Но уже в старших классах на это обращают некоторое внимание!

Почему единица площади(и в том числе квадрата) обозначают двойкой чуть выше буквеного выражения!?

Если мы вспомним, что площадь квадрата равна умноженной длины стороны на себя и напишем единицу измерения… то мы увидим откуда берется двойка…

Давайте покажем на примере…

Пусть надо найти площадь квадрата со стороной 12 см.

Так и записываем в формулу :

S = 12см * 12см

Далее никуда единицу измерения не убираем, а умножаем их между собой, вот отсюда и получается квадратные сантиметры(или другая мера длины в квадрате) :

12*12(см*см) = 12²см² = 144см²

Как найти площадь квадрата зная радиус вписанной окружности!?

Задача :

Как найти площадь квадрата зная радиус вписанной окружности!?

Это очень простая задача!

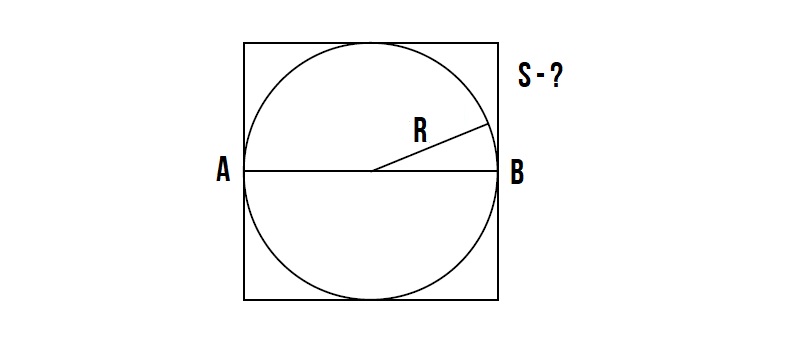
Диаметр вписанной окружности равна стороне квадрата.

Диаметр окружности равен 2R.

Значит сторона квадрата равна 2R.

Далее вспоминаем формулу площади квадрата — S = a², где a — сторона квадрата, которая равна = 2R.

Значит площадь квадрата равна S = (2R)²

Как найти площадь квадрата зная радиус описанной окружности!?

Задача :

Как найти площадь квадрата зная радиус описанной окружности!?

Данная задача такая же простая, как и выше описанная!

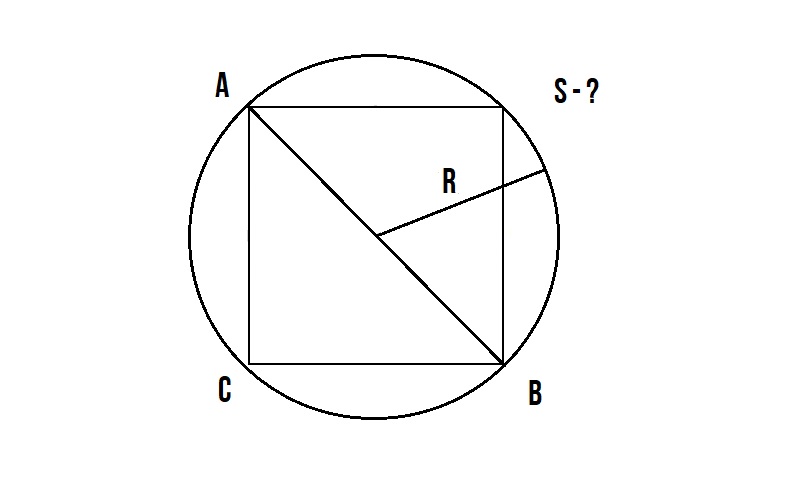
У нас известен радиус окружности описанной вокруг квадрата.

Диаметр окружности AB равен диагонали квадрата AB и мы знаем, что диаметр окружности равен двум радиусам d = 2R.

По диагонали квадрата мы уже один раз высчитывали площадь здесь -> S = d²/2

Далее подставляем S = (2R)²/2

Найти площадь квадрата онлайн

Для того чтобы посчитать площадь квадрата онлайн, вам требуется в поле :

Сторона квадрата — заполнить значением стороны квадрата.

И нажать кнопку посчитать.

Источник

Информация по назначению калькулятора

В плоской (евклидовой) геометрии квадрат — это правильный многоугольник с четырьмя сторонами. Его также можно рассматривать как частный случай прямоугольника, поскольку он имеет четыре прямых угла и параллельные стороны. Аналогично, это также частный случай ромба, параллелограмма и трапеции.

Квадратом называют правильный прямоугольник, все стороны и углы которого равны между собой.

В неевклидовой геометрии квадраты, как правило, представляют собой многоугольники с четырьмя равными сторонами и равными углами.

В сферической геометрии квадрат — это многоугольник, края которого представляют собой большие дуги окружности на равном расстоянии, которые пересекаются под равными углами. В отличие от квадрата плоской геометрии, углы такого квадрата больше прямого угла.

В гиперболической геометрии квадратов с прямыми углами не существует. Скорее всего, квадраты в гиперболической геометрии имеют углы меньше прямых углов.

Онлайн калькулятор предназначен для нахождения параметров квадрата, таких как:

Длины сторон

— равны между собой

(AB=BC=CD=DA)

Периметр

— равен сумме всех сторон, или стороне квадрата умноженной на 4

(P=AB+BC+CD+DA=AB*4)

Площадь

— равна произведению двух сторон, или сторона в квадрате

(S=AB*BC=AB^2)

Диагональ

— является гипотенузой прямоугольного равнобедренного треугольника внутри квадрата с катетом AB и равна стороне квадрата умноженной на квадратный корень из 2

(AC=AB*sqrt{2})

Углы

— всегда равны 90 градусов

Радиус Вписанной и Описанной окружностей
Диаметр Вписанной и Описанной окружностей
Длина Вписанной и Описанной окружностей
Площадь Вписанной и Описанной окружностей

Диаметр описанной окружности равен длине диагонали квадрата, а диаметр вписанной окружности равен длине стороны квадрата

Источник