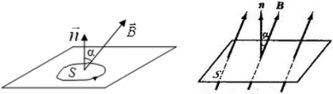
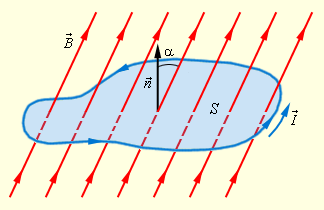
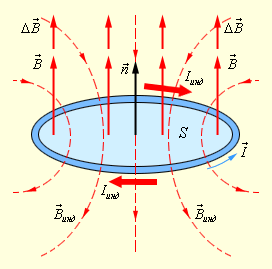
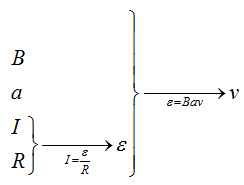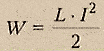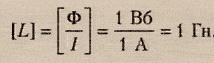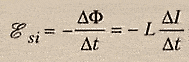Магнитный поток, проходящий через площадь S равен:
Ф = BScosα;
где:
Ф ― величина магнитного потока [Вб],
S ― площадь контура [м2],
B ― индукция магнитного поля [Тл],
α ― угол между нормалью $overrightarrow{n}$ к площади контура и вектором индукции магнитного поля $overrightarrow{B}$.
Если вектор индукции магнитного поля $overrightarrow{B}$ перпендикулярен площади контура, то магнитный поток равен:
Ф = BScos90° = BS;
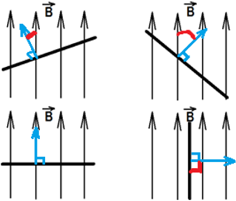
Максимальное значение потока будет тогда, когда косинус будет максимальным (cosα = 1), то есть угол между вектором $overrightarrow{B}$ и вектором нормали к пластинке равен 0°, чему соответствует картинка 3. Наименьшее же значение потока будет тогда, когда косинус будет равен нулю (cosα = 0), то есть угол между нормалью к пластинке и вектором индукции равен 90°, чему соответствует картинка 4.
Электромагнитная индукция ― явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через контур. Если контур разомкнут, то на его концах наблюдается разносность потенциалов, равная ЭДС индукции.
ЭДС электромагнитной индукции возникает только тогда, когда изменяется магнитный поток.
Закон Фарадея об электромагнитной индукции и гласит, что индуцируемая ЭДС прямо пропорциональна скорости изменения магнитного потока:
$varepsilon_i = -frac{Delta text{Ф}}{Delta t}$
где:
$varepsilon_i $ ― ЭДС электромагнитной индукции [B],
$frac{Delta text{Ф}}{Delta t}$ ― скорость изменения магнитного потока [Вб/с],
∆Ф ― изменение магнитного потока [Вб],
∆t ― время, за которое происходит это изменение [c].
Кроме того, ЭДС индукции равна производной магнитного потока по времени:
$varepsilon_i = -text{Ф}_t’$
где:
- ― ЭДС электромагнитной индукции [B],
- ― производная магнитного потока по времени [Вб/с].
Задача 1
Замкнутый контур площадью S из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. В контуре возникают колебания тока с амплитудой iм = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos (bt), где a = 6 · 10-3Тл, b = 3500 c-1. Электрическое сопротивление контура R = 1,2 Ом. Чему равна площадь контура?
Решение:
Обратите внимание на величины, данные в условии. Они здесь совсем не такие, к которым вы привыкли, потому что не дано значение магнитного поля, а дана зависимость магнитного поля от времени. Посмотрим, как это скажется на решении задачи.
Поскольку магнитное поле, а вместе с ним и поток меняются, то будет возникать ЭДС индукции, именно это ЭДС и вызовет электрический ток, поэтому запишем закон электромагнитной индукции.
По закону электромагнитной индукции $varepsilon_i = -frac{Delta text{Ф}}{Delta t}$
ЭДС — это изменение магнитного потока за время. Ничего в определении ЭДС не сказано про это самое время. Дело в том, что изменение какой-то величины за небольшой промежуток времени называется производной по времени. То есть наше ЭДС, которое является изменением магнитного потока за небольшой промежуток времени, это просто производная магнитного потока по времени $varepsilon_i = -text{Ф}_t’$
И это очень важный момент, без которого мы не сможем решить такого рода задачу.
Теперь посчитаем ЭДС индукции.
Напишем, чему равен магнитный поток Ф = BS = acos (bt) · S.
ЭДС индукции — это производная магнитного потока по времени. Теперь придётся вспомнить немного математики. Множители “a” и “S” перед косинусом не зависят от времени, поэтому производная их не трогает, а вот у косинуса в скобках стоит зависимость от времени, поэтому именно от косинуса производную и нужно взять.
Обратите внимание на полученную формулу магнитного потока. В ней стоит просто множитель aS перед сложной функцией косинуса
$text{Ф} underset{text{множитель}}{underbrace{aS}} ;; cdot ;; underset{text{сложная функция}}{underbrace{cos(bt)}}$.
Взяв производную от этой функции, получаем Ф´ = –abS · sin (bt). А теперь, раз мы знаем производную магнитного потока, значит, знаем и ЭДС индукции, потому что $varepsilon_i = -text{Ф}_t’$
Подставив сюда значение производной, получим $varepsilon_i = -text{Ф}_t’$ = abS · sin (bt).
Мы получили значение ЭДС. Кроме этого, мы знаем сопротивление и максимальную силу тока, поэтому запишем закон Ома.
По закону Ома $I = frac{varepsilon}{R}$ , подставив сюда значение ЭДС, получаем $I = frac{abScdot sin(bt)}{R}$.
Мы получили зависимость силы тока от времени.
Из-за синуса, который стоит в этой формуле, ток постоянно меняет свое значение, то он становится больше, то меньше, поскольку синус меняет своё значение от -1 до 1.
В условии дано максимальное значение силы тока, которое протекает по контуру. Когда эта величина будет максимальной? В тот момент, когда синус будет максимальным, то есть равный единице. Поэтому запишем sin (bt) = 1.
Максимальное значение тока будет в тот момент, когда будет максимальным значение ЭДС индукции, то есть когда, $I_{max} = frac{abS}{R}$.
Отсюда можно легко выразить площадь контура $S = frac{I_{max}R}{ab}$, подставив сюда все значения, получим $S = frac{I_{max}R}{ab} = frac{35cdot 10^{-3} Acdot 1,2text{Ом}}{6cdot 10^{-3}text{Тл} cdot 35000c^{-1}} = 0,002text{м}^2$
Ответ: 0,002
Как видно из формулы магнитного потока Ф = BScosα, изменение магнитного потока может быть вызвано разными факторами:
- увеличением или уменьшением модуля индукции магнитного поля (т. е. величины $frac{Delta B}{Delta t}$);
- изменением направления вектора магнитного поля (т. е. изменением угла α);
- деформацией контура, причем такой деформацией, при которой изменяется площадь контура (т. е. изменением величины $frac{Delta S}{Delta t}$ );
- изменением нескольких из этих величин одновременно.
Таким образом, изменение модуля или направление вектора магнитной индукции или площади контура неизбежно приводят к тому, что в контуре возникает электродвижущая сила.
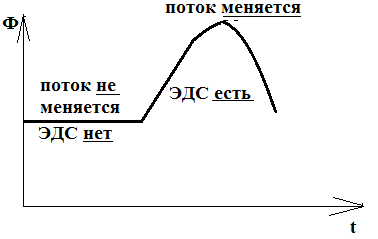
Если нарисовать график зависимости магнитного потока, то он может выглядеть либо так: тогда поток не будет менятьсяи ЭДС не возникает.
Либо так, тогда будет меняться поток и возникать ЭДС:
Знак «минус» перед скоростью изменения магнитного потока в формуле отражает правило Ленца: индуцированный ток всегда направлен так, чтобы магнитное поле, которое он создает, препятствовало изменению магнитного потока.
Если магнитный поток, проходящий через площадь контура, уменьшается, то магнитное поле индуцированных токов будет стремиться его увеличить.
Если поток увеличивается ― магнитное поле индуцированных токов будет стремиться его уменьшить.
Задача 2
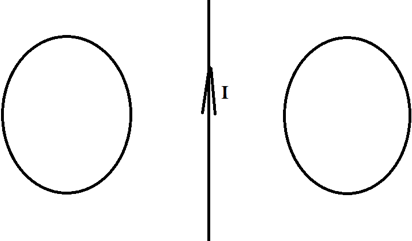
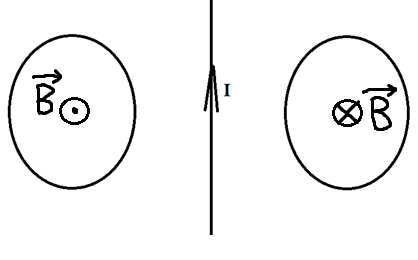
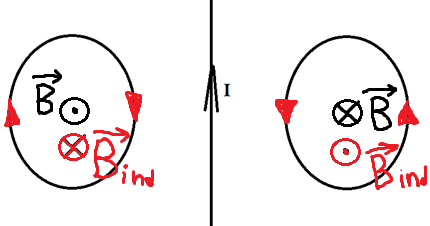
Два проводящих кольца расположены относительно проводника с током в одной плоскости, как это показано на рисунке. В каком направлении будет индуцироваться ток в этих кольцах, если начать двигать их в направлении проводника?
Решение:
Первым делом необходимо понять, как вообще может возникать индуцированный ток, если даже магнитного поля нет?
Его направление мы можем определить по правилу правого винта. Отметим это на рисунке.
Теперь эти два проводника начинают двигать. Разве от этого меняется поток? Ведь площадь остаётся та же самая, угол между нормалью и вектором тоже не меняется. Однако, чем ближе к проводнику с током, тем сильней поле, а чем дальше от него, тем слабее! Поэтому, когда мы двигаем кольца к проводнику, мы увеличиваем поток, ведь ближе поле сильнее. Значит, будет появляться ток, а его направление можно определить по правилу Ленца. Что нам говорит правило Ленца?
Раз поток увеличивается, то по правилу Ленца ток будет индуцироваться так, чтобы уменьшить поток, то есть магнитное поле в левом кольце будет направлено от нас, а в правом ─ на нас. А значит, по правилу правого винта мы можем определить, что ток будет течь по часовой стрелке слева и против часовой стрелки справа.
Движение проводников
Если к концам проводника, движущегося в магнитном поле, подключить вольтметр, то прибор покажет наличие разности потенциалов на концах проводника. Таким образом, когда проводник перемещается в области с магнитным полем, в нем возникает электромагнитная движущая сила (ЭДС).
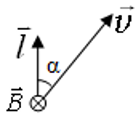
Согласно закону Лоренца, в проводнике, движущемся в магнитном поле, создается ЭДС $|varepsilon_i| = Blvsinalpha$;
где:
$varepsilon_i$― ЭДС электромагнитной индукции [B],
B ― индукция магнитного поля [Тл],
l ― длина проводника [м],
v ― скорость движения проводника [м/с],
α ― угол между направлением вектора скорости $overrightarrow{v}$ и длиной проводника $overrightarrow{l}$ , если вектор индукции магнитного поля $overrightarrow{B}$перпендикулярен проводнику и вектору скорости его движения: $overrightarrow{B} perp overrightarrow{v}, overrightarrow{B} perp overrightarrow{l}$
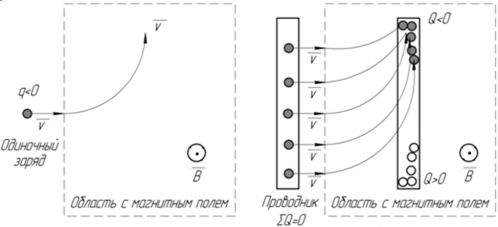
Используя силу Лоренца, можно получить это определение ЭДС. Сила Лоренца ― это проявленное действие магнитного поля на заряженную частицу.
В проводнике присутствует большое количество свободных зарядов (именно это отличает проводники от диэлектриков), и на каждый из зарядов действует сила Лоренца, перемещая их по проводнику так, что в одной его части скапливается отрицательный заряд, а в другой, соответственно, положительный. Это распределение зарядов и является физической основой для возникновения электродвижущей силы.
На рисунке показано как сила Лоренца, действующая на каждый из зарядов проводника, создаёт ЭДС в проводнике. Если одиночный отрицательный заряд попадает в магнитное поле, направленное от нас, то, согласно правилу левой руки, направление его движения изменяется так, как показано на рисунке. Если в область с таким же магнитным полем входит проводник, суммарный заряд которого равен нулю, но внутри которого находятся электроны, способные свободно перемещаться в проводнике, то электроны стекаются в один конец проводника. Так как электроны переместились в один конец проводника, то этот конец приобретает отрицательный заряд, а противоположный ему ― положительный. Таким образом, в проводнике возникает разность потенциалов и электродвижущая сила.
В некоторых случаях удобно решать задачи, используя определение ЭДС через закон Лоренца (обычно это задачи о движении прямолинейного проводника в поле), в других ― через закон Фарадея.
В проводнике, движущемся в магнитном поле, образуется разность потенциалов U = lvBsinα;
где:
U — разность потенциалов [В],
l — длина проводника [м],
v — скорость движения проводника $big[ frac{text{м}}{c} big]$
B — индукция магнитного поля [Тл],
α — угол между направлением скорости и длиной проводника.
В случае, если есть какой-то замкнутый контур, то ЭДС в нем возникает только тогда, когда меняется магнитный потокчерез этот контур. В случае же тонкого стержня, для которого нельзя применить понятия магнитного потока, потому что у него просто нет площади, ЭДС возникает при движении в постоянном магнитном поле.
В случае, если в задаче дана проводящая рамка или контур, для определения ЭДС (напряжения) используем формулу $varepsilon_i = — frac{Delta text{Ф}}{Delta t}$
В случае, если в задачи дан проводник, движущейся в поле, для определения ЭДС (напряжения) используем формулу $varepsilon$ =U= lvBsinα.
Задача 3
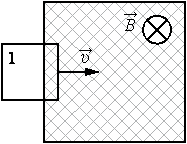
В заштрихованной области на рисунке действует однородное магнитное поле, перпендикулярное плоскости рисунка с индукцией В = 0,1 Тл. Квадратную проволочную рамку, сопротивление которой 10 Ом и длина стороны 10 см, перемещают в этом поле в плоскости рисунка поступательно равномерно с некоторой скоростью υ. При попадании рамки в магнитное поле в положении 1 в ней возникает индукционный ток, равный 1 мА. Какова скорость движения рамки?
Решение:
Составим цепочку.
Зная силу тока и сопротивление, что можно найти? Мы сможем найти напряжение, то есть ЭДС, а ЭДС, уже можно легко связать со скоростью движения рамки.
Составим цепочку. Мы знаем магнитное поле (В), длину стороны (a), сопротивление (R) и силу тока (I), а найти нужно скорость(v).
Зная ток и сопротивление, что сразу можно найти? Напряжение, то есть ЭДС, которое мы сможем найти по закону Ома.
А связать ЭДС с индукцией поля, стороной рамки и скоростью движения очень легко, воспользовавшись той формулой, которую мы получили в прошлой задаче.
Пройдёмся вдоль этой цепочки.
Запишем закон Ома $I = frac{varepsilon}{R}$, подставив сюда формулу для ЭДС, которую мы получили в прошлой задаче, отбросив знак «минус» получим $I = frac{varepsilon}{R} = frac{Bav}{R}$отсюда выразим скорость, и, подставив все величины, получим $v = frac{IR}{Ba} = frac{1cdot 10^{-3} Acdot 10text{Ом}}{0,1 text{Тл} cdot 0,1 text{м}} = 1 frac{text{м}}{c}$
Ответ: 1
Магнитные потоки представляют собой воображаемые линии, проникающие сквозь материал при нахождении в электромагнитном или магнитном поле. Магнитный поток и площадь взаимозависимы.
Магнитный поток и напряженность поля зависят от площади проводящего материала и линейно зависят от площади. По мере увеличения площади проводящего материала увеличивается и магнитный поток через проводник.
Как магнитный поток связан с площадью?
Магнитный поток через материал, находящийся в поле, будет тем больше, чем больше площадь проводника.
Магнитный поток, проникающий через проводящий материал, будет увеличиваться, если площадь материала, находящегося в поле, больше. Следовательно, магнитный поток прямо пропорционален площади материала вместе с магнитным полем.
Магнитное поле напрямую связано с площадью проводника соотношением
Здесь A — площадь, через которую проходят линии магнитного поля, B — магнитное поле, а θ — угол между направлением магнитного поля и линиями магнитного потока.
Зависит ли магнитный поток от площади?
Магнитный поток действительно зависит от площади, поскольку поток через материал увеличивается, если площадь материала больше.
Магнитный поток является очень важной концепцией для определения чистого магнитного потока через материал, и он напрямую зависит от площади. Чем больше площадь проводника, тем больше потока будет проникать через материал.
Как найти магнитный поток от площади?
Магнитный поток представляет собой интеграл магнитного поля на единицу площади.
Магнитный поток из области можно найти, зная напряженность магнитного поля в области и общую площадь проводника. Магнитный поток через этот проводник является произведением обоих.
Рассмотрим плоскую проводящую область в области магнитного поля. Пусть da будет маленьким элементом, имеющим площадь поверхности в один квадратный метр. Линии полного магнитного поля dφ проходят через этот небольшой элемент da в направлении, образующем угол θ, как показано на рисунке ниже.
Магнитный поток, проходящий через единицу площади, является целым кратным магнитного поля в рассматриваемой области и площади da. Следовательно, магнитный поток определяется соотношением
Магнитное поле является общим термином, поскольку оно не является переменным в этой ситуации, поэтому мы можем переписать приведенное выше уравнение как
Интеграл от da представляет собой общую площадь материала в магнитном поле. Решая интеграл, получаем:
Здесь θ — угол, образуемый силовыми линиями магнитного поля с направлением поля.
Если силовые линии перпендикулярны направлению магнитного поля, то θ=0 и, следовательно, мы получаем приведенное выше выражение как,
ф=ВА
Магнитное поле является произведением создаваемого магнитного поля и площади проводника, через которую проходят силовые линии магнитного поля. Это уравнение дает связь между магнитным потоком и площадью.
Как меняется магнитный поток с площадью?
Магнитное поле изменяется в зависимости от площади намагничивающего материала.
Поскольку магнитный поток напрямую зависит от площади проводящего материала в поле, магнитное поле будет уменьшаться, если конфигурация материала уменьшается, и увеличивается, если площадь проводящего материала увеличивается.
Напряженность магнитного поля увеличивается, если увеличивается магнитный поток, проникающий через единицу площади материала. Это явно зависит от типа магнитного материала, находящегося в поле. Ферромагнитный материал пропускает больший магнитный поток через материал, поскольку магнитные диполи легко размещаются в направлении магнитного поля.
Как найти площадь магнитного потока?
Площадь магнитного потока – это общая площадь материала, через которую проходит магнитный поток.
Площадь магнитного потока — это отношение магнитного потока через площадь к полному магнитному полю. Площадь магнитного потока также может быть рассчитана путем деления магнитного потока, протекающего через материал, на плотность магнитного потока через единицу площади.
Мы знаем, что плотность магнитного потока — это общее число силовых линий магнитного поля, проходящих через единицу площади проводника. Это дается формулой,
Здесь,
— плотность магнитного потока через единицу площади, φ — магнитный поток, A — площадь материала.
Следовательно, площадь можно рассчитать, если мы знаем плотность магнитного потока на единицу площади и чистый поток через материал, изменив приведенную выше формулу следующим образом:
Площадь магнитного потока есть отношение магнитного потока к плотности магнитного потока через единицу площади.
График зависимости магнитного потока от площади
Магнитный поток прямо пропорционален площади материала и, следовательно, по мере увеличения площади материала магнитный поток должен увеличиваться. Чем больше площадь, тем сильнее магнитный поток проникает через материал.
Следовательно, график зависимости магнитного потока от площади выглядит так, как показано ниже:
График четко показывает зависимость между магнитным потоком и площадью. Чем больше площадь намагничивающего материала, тем больше и больше магнитного потока будет проникать через него. И, следовательно, магнитный поток через материал будет увеличиваться.
Плотность магнитного поля не изменится с увеличением площади материала. Плотность магнитного потока для конкретного материала, создающего фиксированное магнитное поле, останется постоянной. В то время как магнитный поток, проходящий через материал, будет меняться.
Предположим, что магнитное поле, создаваемое определенным намагничивающимся материалом, равно 2 Тл. Различные плоские листы с переменными площадями из одного и того же материала находятся в одной и той же электромагнитной области, и рассчитывается магнитный поток через материал. Было обнаружено, что силовые линии магнитного потока остаются параллельными направлению магнитного поля.
Были отмечены следующие данные,
| Площадь (м2) | Магнитный поток (Вб) |
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
| 5 | 10 |
Давайте построим график зависимости магнитного потока от площади, используя приведенные выше данные, и поймем концепцию.
Вот график магнитного потока и площади каждого плоского листа, находящегося в области магнитного поля. На графике видно, что магнитный поток линейно увеличивается с площадью. С увеличением напряженности магнитного поля увеличивается общее число проникающих через площадь потоков.
Чему равен магнитный поток через единицу площади проводника, если магнитное поле B0a2? Обратите внимание, что а — это площадь, а В.0 начальное магнитное поле?
Данный: B=B0a2
A = 1 м2
Магнитный поток через единицу площади можно рассчитать, используя выражение
Подставляя значение B в выражение, получаем:
Вычитая общий член из интеграла, мы имеем,
Решая приведенный выше интеграл, получаем:
Подставив значение площади, получим:
Следовательно, магнитный поток составляет одну треть начального магнитного поля.
Чему равно магнитное поле, если магнитный поток, протекающий через площадь 0.16 м2 1 Вб?
Данный: A = 0.16 м2
φ =1 Втб
Магнитный поток связан с магнитным полем уравнением
φ =ВА
Здесь φ — магнитный поток, A — площадь, B — магнитный поток.
Следовательно, выражение для расчета магнитного поля из магнитного потока:
В=φ/А
Подставляя значения в это выражение, получаем:
Решая это дальше, получаем:
В=6.25 Тл
Следовательно, магнитное поле, в котором находится материал, равно 6.25 T.
Заключение
Магнитный поток находится в прямой зависимости от площади намагничивающего материала. Общее количество магнитных потоков, поступающих в проводник при постоянном магнитном поле, зависит от его площади. Если площадь поверхности проводника увеличить, то магнитный поток через проводник увеличится. Магнитный поток линейно возрастает с площадью.
Вероятно, термин «поток» ассоциируется у вас с потоком воды. Если бы вы хотели описать этот поток количественно, то имели бы в виду определенное количество воды, протекающей через поперечное сечение в определенной точке. Такой поток может нести большое или малое количество воды в зависимости от скорости воды и площади этого поперечного сечения.
Магнитный поток — это физическая величина, тесно связанная с явлением электромагнитной индукции. Это сложная величина, довольно абстрактная. Но, как вы правильно догадались, его название берет свое начало в гидродинамике. Здесь, однако, нет потока материи через поверхность, есть только векторы магнитной индукции B, «пронзающие» поверхность и иногда «скользящие» по ней.
Представьте себе однородное магнитное поле, описываемое вектором магнитной индукции B. Мы помещаем плоскую поверхность с полем S в это поле совершенно произвольным образом, то есть под любым углом по отношению к вектору B (рис. 1). Теперь определим вектор B, перпендикулярный плоскости поверхности. Пусть длина этого вектора равна величине поверхности.
Потоком вектора магнитной индукции ФB через поверхность S называется скалярное произведение векторов B и S.
Итак можно дать следующее определение термину «магнитный поток»:
Магнитный поток — это поток вектора магнитной индукции B через некоторую поверхность. Для бесконечно малого участка равен произведению модуля | B | на площадь участка dS и косинус угла α между B и нормалью n к плоскости участка. Для поверхности конечных размеров находится как сумма (интеграл) по её малым фрагментам.
Википедия
Зависимости магнитного потока
Используя формулу, можно увидеть, что магнитный поток зависит от трех переменных: магнитного поля B, площади S и угла α.
Магнитный поток линейно зависит от B и S. Например, если увеличить площадь S, но оставить магнитное поле B и угол α прежними, то магнитный поток будет больше. Поэтому большая площадь означает большой поток, а маленькая площадь — маленький магнитный поток.
Если, с другой стороны, увеличить магнитное поле B, то магнитный поток также увеличится. Сильное магнитное поле приводит к большому потоку, слабое поле — к малому магнитному потоку.
В целом, чем больше магнитное поле B или площадь S, тем больше магнитный поток.
Ситуация с углом α немного сложнее. Представьте, что ваша поверхность перпендикулярна магнитному полю, тогда ваш угол α = 0° . Здесь у вас самый большой магнитный поток. Если теперь шаг за шагом увеличивать угол, магнитный поток уменьшается. Когда вы достигаете α = 90°, магнитный поток равен нулю, потому что магнитное поле параллельно поверхности. После этого он снова начинает увеличиваться.
Единица измерения и обозначение магнитного потока
Магнитное поле B имеет единицу Тесла (T), а площадь — единицу квадратный метр м2 .
Поток является скалярной величиной и его единицей измерения является вебер (Вб): 1 Вб = 1 Т * м2 , то есть [Ф] = Т * м2 . Обозначается магнитный поток как Ф (символ формулы — греческая фи).
Примеры
Приведенные ниже примеры дадут вам лучшее понимание того, что представляет собой новая концепция и аналогия с потоком воды.
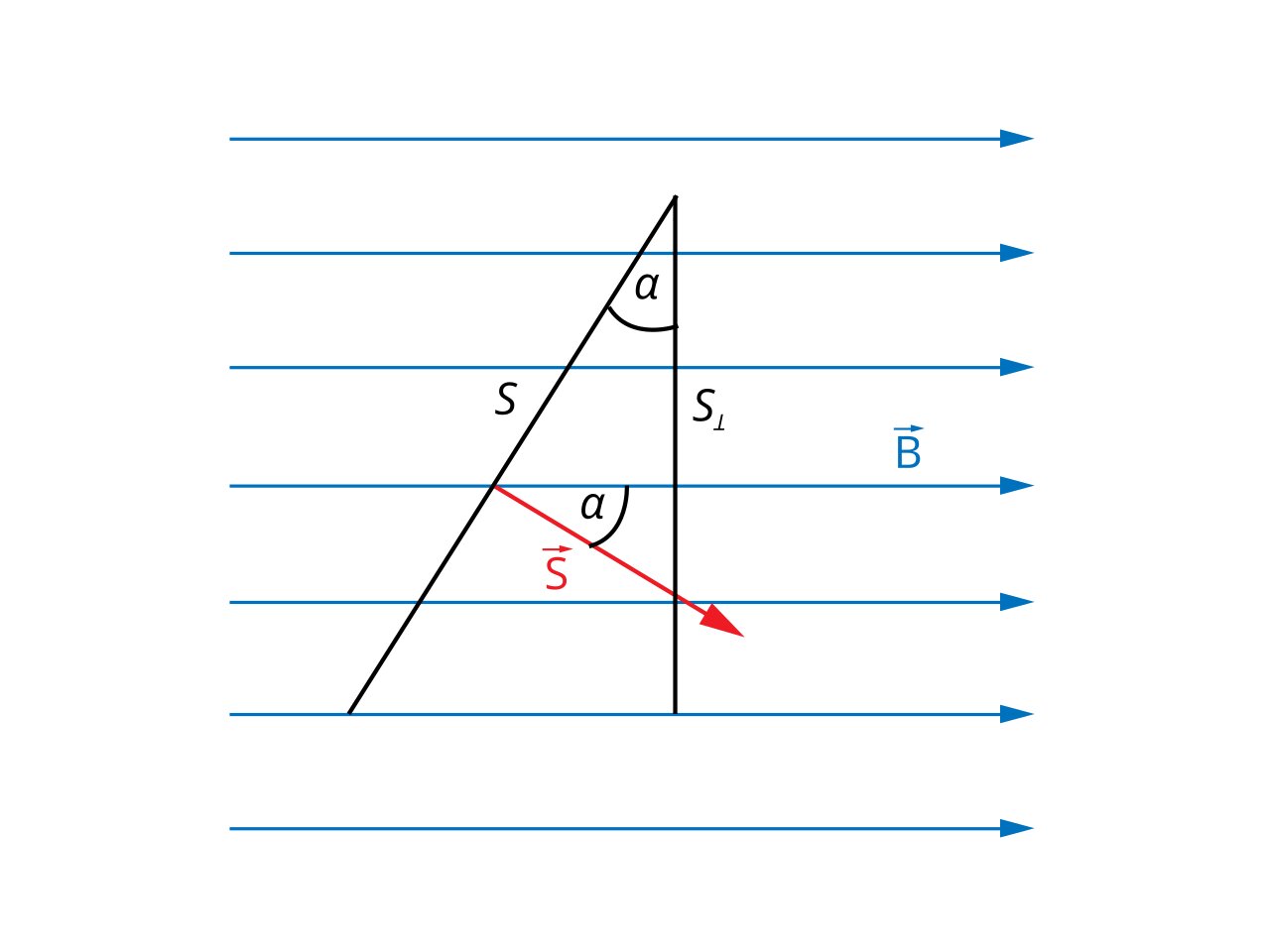
- В случае, показанном на рис. 2, поток магнитного поля с магнитной индукцией B через поверхность S составляет: ФB = B * S и при этом его значение максимально, так как:
2. А в каком случае при ненулевой магнитной индукции ФB = 0 ?
Определение магнитного потока показывает, что это тот случай, когда:
потому что cos 90° = 0.
На рис. 3 мы видим, как в этой ситуации располагается плоская поверхность относительно векторов магнитной индукции.
Обратите внимание, что ФB можно представить как произведение В и S⟂, где S⟂ = S * cos α. Аналогично, вы всегда можете рассчитать величину потока магнитного поля, умножив составляющую магнитной индукции, перпендикулярную поверхности, на величину площади поверхности (см. рис. 4а. и 4б.).
Как можно рассчитать поток магнитного поля, если поле неоднородно и/или поверхность искривлена? Мы делим поверхность, через которую мы должны вычислить поток, на такие маленькие участки, что можно считать, что они плоские и поле однородное. Все это для того, чтобы можно было применить определение потока. Поэтому мы вычисляем небольшие «потоки» и суммируем их. Описанная процедура называется вычислением поверхностного интеграла, который записывается в виде:
Вычислять такие интегралы совсем не обязательно, но полезно понимать смысл такой процедуры.
Магнитный поток
Автор:
Субботин Б.П.
На
картинке показано однородное магнитное
поле. Однородное означает одинаковое
во всех точках в данном объеме. В поле
помещена поверхность с площадью S. Линии
поля пересекают поверхность.
Определение
магнитного потока:
Магнитным
потоком Ф через поверхность S называют
количество линий вектора магнитной
индукции B, проходящих через поверхность
S.
Формула
магнитного потока:
Ф
= BS cos α
здесь
α — угол между направлением вектора
магнитной индукции B и нормалью к
поверхности S.
Из
формулы магнитного потока видно, что
максимальным магнитный поток будет при
cos α = 1, а это случится, когда вектор B
параллелен нормали к поверхности S.
Минимальным магнитный поток будет при
cos α = 0, это будет, когда вектор B
перпендикулярен нормали к поверхности
S, ведь в этом случае линии вектора B
будут скользить по поверхности S, не
пересекая её.
А
по определению магнитного потока
учитываются только те линии вектора
магнитной индукции, которые пересекают
данную поверхность.
Измеряется
магнитный поток в веберах (вольт-секундах):
1 вб = 1 в * с. Кроме того, для измерения
магнитного потока применяют максвелл:
1 вб = 108 мкс.
Соответственно 1 мкс = 10-8 вб.
Магнитный
поток является скалярной величиной.
ЭНЕРГИЯ
МАГНИТНОГО ПОЛЯ ТОКА
Вокруг
проводника с током существует магнитное
поле, которое обладает энергией.
Откуда
она берется? Источник тока, включенный
в эл.цепь, обладает запасом энергии.
В
момент замыкания эл.цепи источник тока
расходует часть своей энергии на
преодоление действия возникающей ЭДС
самоиндукции. Эта часть энергии,
называемая собственной энергией тока,
и идет на образование магнитного
поля.
Энергия магнитного поля
равна собственной
энергии тока.
Собственная
энергия тока численно равна работе,
которую должен совершить источник тока
для преодоления ЭДС самоиндукции, чтобы
создать ток в цепи.
Энергия
магнитного поля, созданного током, прямо
пропорциональна квадрату силы тока.
Куда
пропадает энергия магнитного поля после
прекращения тока? — выделяется ( при
размыкании цепи с достаточно большой
силой тока возможно возникновение искры
или дуги)
4.1. Закон электромагнитной индукции. Самоиндукция. Индуктивность
Основные
формулы
· Закон
электромагнитной индукции (закон
Фарадея):
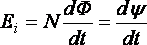
(39)
где – эдс индукции;
–
полный магнитный поток (потокосцепление).
· Магнитный
поток, создаваемый током в контуре,
,
(40)
где –
индуктивность контура;–
сила тока.
· Закон
Фарадея применительно к самоиндукции
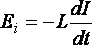
(41)
· Эдс индукции, возникающая при
вращении рамки с током в магнитном поле,
,
(42)
где –
индукция магнитного поля;–
площадь рамки;–
угловая скорость вращения.
· Индуктивность
соленоида
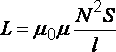
(43)
где –
магнитная постоянная;–
магнитная проницаемость вещества;–
число витков соленоида;–
площадь сечения витка;–
длина соленоида.
· Сила
тока при размыкании цепи
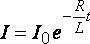
(44)
где –
установившаяся в цепи сила тока;–
индуктивность контура,–
сопротивление контура;–
время размыкания.
· Сила
тока при замыкании цепи
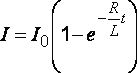
(45)
· Время
релаксации
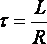
(46)
Примеры
решения задач
Пример
1.
Магнитное
поле изменяется по закону ,
где=
15 мТл,. В
магнитное поле помещен круговой
проводящий виток радиусом = 20
см под угломк
направлению поля (в начальный момент
времени). Найти эдс индукции, возникающую в
витке в момент времени=
5 с.
Решение
По
закону электромагнитной индукции возникающая в
витке эдс индукции 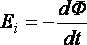
где–
магнитный поток, сцепленный в витке.
,
где –
площадь витка,;
– угол
между направлением вектора магнитной
индукциии
нормалью к контуру:.
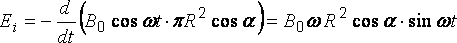
Подставим
числовые значения: =
15 мТл,,
= 20
см = = 0,2 м,.
Вычисления
дают .
|
Пример В Решение При |
|
По
закону Фарадея ,
где,
тогда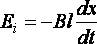
но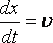
поэтому.
Так, .
Знак
«–» показывает, что эдс индукции
и индукционный ток направлены против
часовой стрелки.
САМОИНДУКЦИЯ
Каждый
проводник, по которому протекает эл.ток,
находится в собственном магнитном поле.
При
изменении силы тока в проводнике меняется
м.поле, т.е. изменяется магнитный поток,
создаваемый этим током. Изменение
магнитного потока ведет в возникновению
вихревого эл.поля и в цепи появляется
ЭДС индукции.
Это
явление называется самоиндукцией.Самоиндукция —
явление возникновения ЭДС индукции в
эл.цепи в результате изменения силы
тока.
Возникающая при этом ЭДС
называется ЭДС
самоиндукции
Проявление
явления самоиндукции
Замыкание
цепи
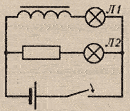
замыкании в эл.цепи нарастает ток, что
вызывает в катушке увеличение магнитного
потока, возникает вихревое эл.поле,
направленное против тока, т.е. в катушке
возникает ЭДС самоиндукции, препятствующая
нарастанию тока в цепи ( вихревое поле
тормозит электроны).
В результатеЛ1
загорается позже, чем
Л2.
Размыкание
цепи
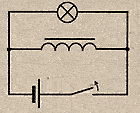
размыкании эл.цепи ток убывает, возникает
уменьшение м.потока в катушке, возникает
вихревое эл.поле, направленное как ток
( стремящееся сохранить прежнюю силу
тока) , т.е. в катушке возникает ЭДС
самоиндукции, поддерживающая ток в
цепи.
В результате Л при выключении ярко
вспыхивает.
Вывод
в
электротехнике явление самоиндукции
проявляется при замыкании цепи (эл.ток
нарастает постепенно) и при размыкании
цепи (эл.ток пропадает не сразу).
ИНДУКТИВНОСТЬ
От
чего зависит ЭДС самоиндукции?
Эл.ток
создает собственное магнитное поле .
Магнитный поток через контур пропорционален
индукции магнитного поля (Ф ~ B), индукция
пропорциональна силе тока в проводнике
(B
~ I), следовательно магнитный поток
пропорционален силе тока (Ф ~ I).
ЭДС
самоиндукции зависит от скорости
изменения силы тока в эл.цепи, от свойств
проводника
(размеров и формы) и от
относительной магнитной проницаемости
среды, в которой находится
проводник.
Физическая величина,
показывающая зависимость ЭДС самоиндукции
от размеров и формы проводника и от
среды, в которой находится проводник,
называется коэффициентом самоиндукции
или индуктивностью.
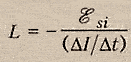
физ. величина, численно равная ЭДС
самоиндукции, возникающей в контуре
при изменении силы тока на 1Ампер за 1
секунду.
Также индуктивность можно
рассчитать по формуле:
где
Ф — магнитный поток через контур, I — сила
тока в контуре.
Единицы
измерения индуктивности в
системе СИ:
Индуктивность
катушки зависит от:
числа витков,
размеров и формы катушки и от относительной
магнитной проницаемости среды
(
возможен сердечник).
ЭДС
САМОИНДУКЦИИ
ЭДС
самоиндукции препятствует нарастанию
силы тока при включении цепи и убыванию
силы тока при размыкании цепи.
Для
характеристики намагниченности вещества
в магнитном поле используетсямагнитный
момент (Рм). Он
численно равен механическому моменту,
испытываемому веществом в магнитном
поле с индукцией в 1 Тл.
Магнитный
момент единицы объема вещества
характеризует его намагниченность
— I,
определяется по формуле:
I= Рм /V,
(2.4)
где V —
объем вещества.
Намагниченность
в системе СИ измеряется, как и напряженность,
в А/м,
величина векторная.
Магнитные
свойства веществ характеризуются объемной
магнитной восприимчивостью — cо , величина
безразмерная.
Если
какое-либо тело поместить в магнитное
поле с индукцией В0,
то происходит его намагничивание.
Вследствие этого тело создает свое
собственное магнитное поле с индукцией В‘,
которое взаимодействует с намагничивающим
полем.
В
этом случае вектор индукции в среде (В)будет
слагаться из векторов:
В
= В0 +
В‘(знак
вектора опущен), (2.5)
где В‘ —индукция
собственного магнитного поля
намагнитившегося вещества.
Индукция
собственного поля определяется магнитными
свойствами вещества, которые характеризуются
объемной магнитной восприимчивостью
— cо ,
справедливо выражение:В‘ = cо В0 (2.6)
Разделим
на m0 выражение
(2.6):
В‘/
mо= cо В0 /m0
Получим: Н‘ = cо Н0 , (2.7)
но Н‘ определяет
намагниченность вещества I,
т.е. Н‘ = I,
тогда из (2.7):
I
= cо Н0.
(2.8)
Таким
образом, если вещество находится во
внешнем магнитном поле с напряженностьюН0,
то внутри него индукция определяется
выражением:
В=В0 +
В‘ =
m0Н0 +m0Н‘ =
m0 (Н0 +
I) (2.9)
Последнее
выражение строго справедливо, когда
сердечник (вещество) находится полностью
во внешнем однородном магнитном поле
(замкнутый тор, бесконечно длинный
соленоид и т.д.).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Явление электромагнитной индукции заключается в том, что в результате изменения во времени магнитного потока, который пронизывает замкнутый проводящий контур, в контуре возникает электрический ток. Открыто это явление было физиком из Великобритании Максом Фарадеем в 1831 году.
Формула магнитного потока
Введем обозначения, необходимые нам для записи формулы. Для обозначения магнитного потока используем букву Ф, площади контура – S, модуля вектора магнитной индукции – B, α – это угол между вектором B→ и нормалью n→ к плоскости контура.
Магнитный поток, который проходит через площадь замкнутого проводящего контура, можно задать следующей формулой:
Φ=B·S·cos α,
Проиллюстрируем формулу.
Рисунок 1.20.1. Магнитный поток через замкнутый контур. Направление нормали n→ и выбранное положительное направление l→ обхода контура связаны правилом правого буравчика.
За единицу магнитного потока в СИ принят 1 вебер (Вб). Магнитный поток, равный 1 Вб, может быть создан в плоском контуре площадью 1 м2 под воздействием магнитного поля с индукцией 1 Тл, которое пронизывает контур по направлению нормали.
1 Вб=1 Тл·м2
Закон Фарадея
Изменение магнитного потока приводит к тому, что в проводящем контуре возникает ЭДС индукции δинд. Она равна скорости, с которой происходит изменение магнитного потока через ограниченную контуром поверхность, взятой со знаком минус. Впервые экспериментально установил это Макс Фарадей. Он же записал свое наблюдение в виде формулы ЭДС индукции, которая теперь носит название Закона Фарадея:
Закон Фарадея:
δинд=-∆Φ∆t
Правило Ленца
Согласно результатам опытов, индукционный ток, который возникает в замкнутом контуре в результате изменения магнитного потока, всегда направлен определенным образом. Создаваемое индукционным током магнитное поле препятствует изменению вызвавшего этот индукционный ток магнитного потока. Ленц сформулировал это правило в 1833 году.
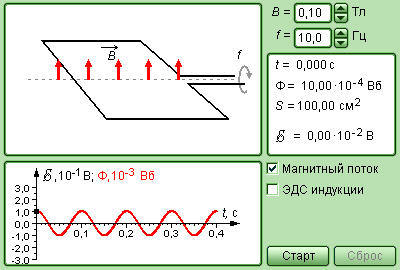
Проиллюстрируем правило Ленца рисунком, на котором изображен неподвижный замкнутый проводящий контур, помещенный в однородное магнитное поле. Модуль индукции увеличивается во времени.
Рисунок 1.20.2. Правило Ленца
Здесь ∆Φ∆t>0, а δинд<0 < 0. Индукционный ток Iинд протекает навстречу выбранному положительному направлению l→ обхода контура.
Благодаря правилу Ленца мы можем обосновать тот факт, что в формуле электромагнитной индукции δинд и ∆Φ∆t противоположны по знакам.
Если задуматься о физическом смысле правила Ленца, то это частный случай Закона сохранения энергии.
Причины возникновения индукционного тока в движущихся и неподвижных проводниках
Причин, по которым может происходить изменение магнитного потока, пронизывающего замкнутый контур, две:
- Изменение магнитного потока вследствие перемещения всего контура или отдельных его частей в магнитном поле, которое не изменяется со временем;
- Изменение магнитного поля при неподвижном контуре.
Перейдем к рассмотрению этих случаев подробнее.
Перемещение контура или его частей в неизменном магнитном поле
При движении проводников и свободных носителей заряда в магнитном поле возникает ЭДС индукции. Объяснить возникновение δинд можно действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца здесь – это сторонняя сила.
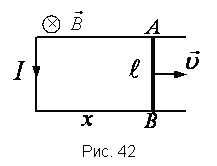
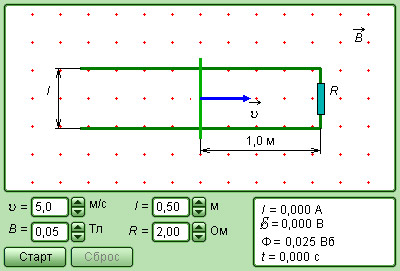
На рисунке мы изобразили пример индукции, когда прямоугольный контур помещен в однородное магнитное поле B→ направленное перпендикулярно плоскости контура. Одна из сторон контура перемещается по двум другим сторонам с некоторой скоростью.
Рисунок 1.20.3. Возникновение ЭДС индукции в движущемся проводнике. Отражена составляющая силы Лоренца, которая действует на свободный электрон
На свободные заряды подвижной части контура воздействует сила Лоренца. Основная составляющая силы Лоренца в данном случае направлена вдоль проводника и связана с переносной скоростью зарядов υ→. Модуль этой сторонней силы равен:
FЛ=eυ→B.
Работа силы FЛ на пути l равна:
A=FЛ·l=eυBl.
По определению ЭДС:
δинд=Ae=υBl.
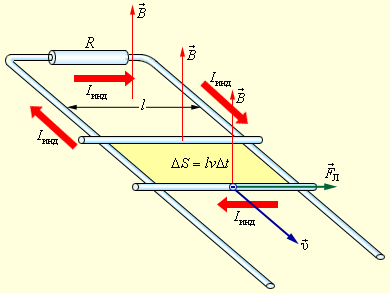
Значение сторонней силы для неподвижных частей контура равно нулю. Для соотношения δинд можно записать другой вариант формулы. Площадь контура с течением времени изменяется на ΔS=lυΔt. Соответственно, магнитный поток тоже будет с течением времени изменяться: ΔΦ=BlυΔt.
Следовательно,
δинд=∆Φ∆t.
Знаки в формуле, которая связывает δинд и ∆Φ∆t, можно установить в зависимости от того, какие направления нормали и направления контура будут выбраны. В случае выбора согласованных между собой по правилу правого буравчика направлений нормали n→ и положительного направления обхода контура l→ можно прийти к формуле Фарадея.
При условии, что сопротивление всей цепи – это R, то по ней будет протекать индукционный ток, который равен Iинд=δиндR. За время Δt на сопротивлении R выделится джоулево тепло:
∆Q=RIинд2∆t=υ2B2l2R∆t
Парадокса здесь нет. Мы просто не учли воздействие на систему еще одной силы. Объяснение заключается в том, что при протекании индукционного тока по проводнику, расположенному в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, которая связана с относительной скоростью движения зарядов вдоль проводника. Благодаря этой составляющей появляется сила Ампера FА→.
Для рассмотренного выше примера модуль силы Ампера равен FA =IBl. Направление силы Ампера таково, что она совершает отрицательную механическую работу Aмех. Вычислить эту механическую работу за определенный период времени можно по формуле:
Aмех=-Fυ∆t=-IBlυ∆t=-υ2B2l2R∆t
Проводник, перемещающийся в магнитном поле, испытывает магнитное торможение. Это приводит к тому, что полная работа силы Лоренца равна нулю. Джоулево тепло может выделяться либо за счет уменьшения кинетической энергии движущегося проводника, либо за счет энергии, которая поддерживает скорость перемещения проводника в пространстве.
Изменение магнитного поля при неподвижном контуре
Вихревое электрическое поле – это электрическое поле, которое вызывается изменяющимся магнитным полем.
В отличие от потенциального электрического поля работа вихревого электрического поля при перемещении единичного положительного заряда по замкнутому проводящему контуру равна δинд в неподвижном проводнике.
В неподвижном проводнике электроны могут приводиться в движение только под действием электрического поля. А возникновение δинд нельзя объяснить действием силы Лоренца.
Первым, кто ввел понятие вихревого электрического поля, был английский физик Джон Максвелл. Случилось это в 1861 году.
Фактически, явления индукции в подвижных и неподвижных проводниках протекают одинаково. Так что в этом случае мы тоже можем использовать формулу Фарадея. Отличия касаются физической причины возникновения индукционного тока: в движущихся проводниках δинд обусловлена силой Лоренца, в неподвижных – действием на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Рисунок 1.20.4. Модель электромагнитной индукции
Рисунок 1.20.5. Модель опытов Фарадея
Рисунок 1.20.6. Модель генератора переменного тока