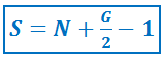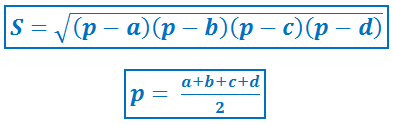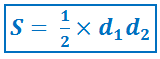ВІДЕОУРОК
Площадь
многоугольника – величина той части плоскости, которую занимает многоугольник.
Площадь
многоугольника – величина, которая имеет такие свойства:
– площадь каждого многоугольника выражается положительным
числом;
– равные многоугольники имеют равные площади;
– площадь многоугольника, состоящая из нескольких
частей, равна сумме площадей всех этих частей;
– за единицу площади принимается площадь единичного
квадрата.
Единичный квадрат –
это квадрат, сторона которого равна единицы длины. Две фигуры с равными площадями
называются равновеликими. Две равные фигуры всегда равновеликие, но не каждые равновеликие
фигуры равны.
Отношение площадей
подобных многоугольников равно квадрату отношения соответствующих сторон (квадрату коэффициента подобности).
ЗАДАЧА:
Стороны двух подобных правильных многоугольников относятся
как 6 : 5,
а разность их площадей равна 77 см2. Найдите
площадь меньшего многоугольника.
РЕШЕНИЕ:
Обозначим сторону меньшего многоугольника
через 5х см, тогда сторона большого – 6х см, где х – некоторое число. Тогда:
ОТВЕТ: 175 см2
Формула Пика.
Площадь многоугольника с целочисленными вершинами равна
N – количество внутренних точек,
G – количество пересечений узлов сетки на границах фигуры.
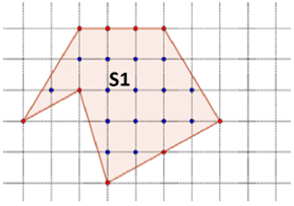
ПРИМЕР:
Найти площадь фигуры с
помощью клеточек.
РЕШЕНИЕ:
Воспользуемся формулой:
S = N + 1/2G – 1.
Сосчитаем количество внутренних точек N,
оно будет равно 15.
Сосчитаем количество внутренних точек пересечений узлов сетки на границах фигуры G, оно будет равно 9.
Подставим эти значения в формулу и найдём
площадь фигуры.
S = 15 + 9/2 –
1 = 18,5 кв. ед.
ЗАДАЧА:
Найдите площадь фигуры с
помощью клеточек.
РЕШЕНИЕ:
Воспользуемся формулой:
S = N + 1/2G – 1.
Сосчитаем количество внутренних точек N,
оно будет равно 5.
Сосчитаем количество внутренних точек пересечений узлов сетки на границах фигуры G, оно будет равно 10.
Подставим эти значения в формулу и найдём
площадь фигуры.
S = 5 + 10/2 –
1 = 9 кв. ед.
ЗАДАЧА:
Найдите площадь фигуры с
помощью клеточек.
РЕШЕНИЕ:
Воспользуемся формулой:
S = N + 1/2G – 1.
Сосчитаем количество внутренних точек N,
оно будет равно 4.
Сосчитаем количество внутренних точек пересечений узлов сетки на границах фигуры G, оно будет равно 12.
Подставим эти значения в формулу и найдём
площадь фигуры.
S = 4 + 12/2 –
1 = 9 кв. ед.
ЗАДАЧА:
Найдите площадь фигуры с
помощью клеточек.
РЕШЕНИЕ:
Воспользуемся формулой:
S = N + 1/2G – 1.
Сосчитаем количество внутренних точек N,
оно будет равно 9.
Сосчитаем количество внутренних точек пересечений узлов сетки на границах фигуры G, оно будет равно 4.
Подставим эти значения в формулу и найдём
площадь фигуры.
S = 9 + 4/2 – 1 =
10 кв. ед.
Площадь четырёхугольника.
Площадь четырёхугольника, вписанного в окружность.
Площадь четырёхугольника, описанного вокруг окружности.
p – полупериметр,
r – радиус вписанной окружности.
Площадь четырёхугольника с перпендикулярными диагоналями (дельтоида) равна половине произведения диагоналей.
ЗАДАЧА:
Площадь треугольника
АВС равна 18 см2.
На стороне АВ обозначили
точки К и D так, что
АК = КD = DВ,
а на стороне АС –
точки F и Е так, что
АF = FЕ = ЕС.
Найдите площадь четырёхугольника DЕFК.
РЕШЕНИЕ:
Начертим чертёж.
Треугольники АВС, АDЕ и АКF подобные, так как у них общий угол и пропорциональные
стороны, которые образуют этот угол.
Пусть АК = х, тогда
АD = 2х, АВ = 3х.
Пользуясь свойством площадей подобных треугольников, получим:
S∆AKF : S∆ABC = AK2 :
AB2,
S∆AKF : 18 = x2 : (3x)2,
SDEFK = S∆ADE
– S∆AKF =
= 8 – 2 = 6 (см2).
ОТВЕТ: 6 см2
ЗАДАЧА:
В треугольнике АВС медиана АК пересекает медиану ВL в точке
L.
Найдите площадь треугольника АВС, если площадь четырёхугольника КСDL равна 5.
РЕШЕНИЕ:
Начертим чертёж.
Проведём третью медиану
СМ.
Три медианы разбивают треугольник на шесть равновеликих треугольников, тогда
S∆CDL = 1/2 SKCDL = 5/2,
S∆ABC = 6∙ S∆CDL = 15.
ОТВЕТ: 15
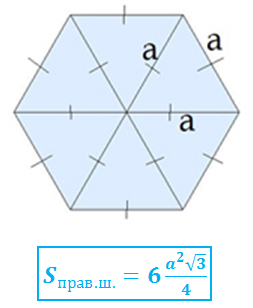
Площадь правильного шестиугольника.
Правильный шестиугольник
состоит из 6 правильных треугольников.
Формула нахождения площади правильного
шестиугольника будет выглядеть следующим образом.
где а – сторона шестиугольника.
ЗАДАЧА:
Найдите радиус окружности, вписанной в правильный
шестиугольник со стороной √͞͞͞͞͞3.
РЕШЕНИЕ:
Для любого многоугольника, в который можно вписать окружность,
верна следующая формула:
S = p∙ r,
где p – полупериметр,
r –
радиус вписанной окружности.
Площадь правильного шестиугольника со
стороной а равна:
а полупериметр
равен 3а, тогда
ОТВЕТ: 1,5
ЗАДАЧА:
Найдите сторону правильного шестиугольника, описанного
около окружности, радиус которой равен √͞͞͞͞͞3.
РЕШЕНИЕ:
Для любого многоугольника, в который можно вписать
окружность, верно
S = p∙ r,
где p – полупериметр,
r –
радиус вписанной окружности.
Площадь правильного шестиугольника со
стороной а равна
полупериметр равен 3а, тогда
а = 2.
ОТВЕТ: 2
Задания к уроку 16
- Задание 1
- Задание 2
- Задание 3
Другие уроки:
- Урок 1. Единицы измерения площади
- Урок 2. Площадь прямоугольника
- Урок 3. Площадь квадрата
- Урок 4. Площадь треугольника
- Урок 5. Площадь прямоугольного треугольника
- Урок 6. Площадь равнобедренного треугольника
- Урок 7. Площадь параллелограмма
- Урок 8. Площадь ромба
- Урок 9. Площадь трапеции
- Урок 10. Площадь равнобедренной трапеции
- Урок 11. Площадь прямругольной трапеции
- Урок 12. Площадь круга и его частей
- Урок 13. Подобие разносторонних треугольников
- Урок 14. Подобие равнобедренных треугольников
- Урок 15. Подобие прямоугольных треугольников
Периметры двух подобных многоугольников относятся как 1 : 10.
Площадь меньшего многоугольника равна 9.
Найдите площадь большего многоугольника.
На этой странице находится вопрос Периметры двух подобных многоугольников относятся как 1 : 10?. Здесь же – ответы на него,
и похожие вопросы в категории Геометрия, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 5 — 9 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.

Геометрия, опубликовано 2018-08-22 14:20:45 by Гость
Периметры двух подобных многоугольников относятся как 1:10. Площадь меньшего многоугольника равна 9. Найдите площадь большего многоугольника.

Ответ оставил Гость
Пусть P1 и Р2 — периметр большего и наименьшего многоугольника
S1 и S2 — площади большего и наименьшего многоугольника
тогда отношение (P2/P1)^2 = S1/S2, получаем
(1/10)^2=9/S2 или 1/100 = 9 /S2 = 900

Не нашли ответа?
Если вы не нашли ответа на свой вопрос, или сомневаетесь в его правильности, то можете воспользоваться формой ниже и уточнить решение. Или воспользуйтесь формой поиска и найдите похожие ответы по предмету Геометрия.
Периметр двух подобных многоугольников…
Задание:
Периметр двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.
Ответ: 50
Решение:
- 1
- 2
- 3
- 4
- 5
Оценка: 3.4 из 10
Комментарии
Всего комментариев: 0
untexave702
Вопрос по математике:
Стороны подобных многоугольников относятся как 2:1, а площадь большего многоугольника равна 36. Найдите площадь меньшего многоугольника.
Трудности с пониманием предмета? Готовишься к экзаменам, ОГЭ или ЕГЭ?
Воспользуйся формой подбора репетитора и занимайся онлайн. Пробный урок — бесплатно!
Ответы и объяснения 2
kfarecalyene
Если все стороны второго многоугольника в 2 раза меньше первого,
то его площадь в 2^2 = 4 раза меньше, то есть равна 36:4 = 9
pomounthithi755
Отношение площадей подобных многоугольников равно квадрату отношения их периметров. Теперь если каждая сторона бОльшего многоугольника по условию в 2 раза больше соответствующей стороны меньшего многоугольника, то и периметр бОльшего многоугольника (как сумма всех сторон) в 2 раза больше периметра меньшего многоугольника.
Пусть S1 — площадь большего мног-ка, S2 — площадь меньшего и Р1, Р2 — соответственно их периметры.
Из всего этого собираем:
Ответ: 9
Знаете ответ? Поделитесь им!
Гость ?
Как написать хороший ответ?
Как написать хороший ответ?
Чтобы добавить хороший ответ необходимо:
- Отвечать достоверно на те вопросы, на которые знаете
правильный ответ; - Писать подробно, чтобы ответ был исчерпывающий и не
побуждал на дополнительные вопросы к нему; - Писать без грамматических, орфографических и
пунктуационных ошибок.
Этого делать не стоит:
- Копировать ответы со сторонних ресурсов. Хорошо ценятся
уникальные и личные объяснения; - Отвечать не по сути: «Подумай сам(а)», «Легкотня», «Не
знаю» и так далее; - Использовать мат — это неуважительно по отношению к
пользователям; - Писать в ВЕРХНЕМ РЕГИСТРЕ.
Есть сомнения?
Не нашли подходящего ответа на вопрос или ответ отсутствует?
Воспользуйтесь поиском по сайту, чтобы найти все ответы на похожие
вопросы в разделе Математика.
Трудности с домашними заданиями? Не стесняйтесь попросить о помощи —
смело задавайте вопросы!
Математика — наука о структурах, порядке и отношениях, исторически сложившаяся на основе операций подсчёта, измерения и описания формы объектов.