Как найти площадь меньшую усеченной пирамиды - Исправление недочетов и поиск решений вместе с Examum.ru

Объем усеченной пирамиды

Рассчитайте объем усеченной пирамиды в зависимости от ее высоты и площадей оснований.

Площадь основания 1

см²

Площадь основания 2

см²

Высота

см

Размерность

Раcсчитать

Оглавление:

📝 Как это работает?
🤔 Частые вопросы и ответы
📋 Похожие материалы
📢 Поделиться и комментировать

🧮 Что такое калькулятор объема усеченной пирамиды?

Калькулятор объема усеченной пирамиды — это инструмент для расчета объема геометрического тела, которое представляет собой усеченную пирамиду.

Усеченная пирамида — это геометрическое тело, которое состоит из двух параллельных и равных многоугольников, называемых основаниями, и боковой поверхности, состоящей из параллельных трапеций. Объем усеченной пирамиды можно вычислить, зная ее высоту и площади оснований.

Калькулятор объема усеченной пирамиды предоставляет пользователю возможность ввести размеры оснований и высоту усеченной пирамиды, после чего вычисляет ее объем.

Как рассчитывается объем усеченной пирамиды?

Объем усеченной пирамиды можно рассчитать с помощью следующей формулы:

V = (1/3) * h * (A + sqrt(A*B) + B)

где V — объем усеченной пирамиды, h — высота усеченной пирамиды, sqrt — означает квадратный корень, A и B — площади большего и меньшего оснований соответственно.

Для расчета объема усеченной пирамиды необходимо знать высоту и площади ее оснований. Первым шагом необходимо определить площади большего и меньшего оснований. Для этого необходимо найти площадь каждого основания (например, площадь треугольника или многоугольника) и обозначить их A и B соответственно.

Затем необходимо найти высоту усеченной пирамиды, которая является расстоянием между плоскостями оснований. Высоту можно измерить прямым измерением или вычислить, зная расстояние между плоскостями оснований и угол между этим расстоянием и боковой гранью.

После этого можно использовать формулу для расчета объема усеченной пирамиды, подставив известные значения площадей оснований и высоты в формулу.

Для чего можно использовать калькулятор объема усеченной пирамиды?

Калькулятор объема усеченной пирамиды можно использовать для расчета объема данной геометрической фигуры, когда известны ее размеры. Это может быть полезно в различных областях, включая:

Архитектуру и строительство: расчет объема усеченной пирамиды может быть полезен для расчета объема строительных материалов, таких как бетон или кирпич, необходимых для создания определенных форм.
Производство: объем усеченной пирамиды может использоваться для расчета объема материала, необходимого для производства определенного изделия.
Образование: расчет объема усеченной пирамиды может быть использован в качестве учебного материала в школах и университетах для изучения геометрии и математики.
Хобби и ремесло: расчет объема усеченной пирамиды может быть полезен в различных хобби и ремеслах, таких как создание моделей или изготовление ювелирных изделий.

Усеченная пирамида как фигура

Усеченная пирамида является интересной геометрической фигурой, которая обладает несколькими уникальными свойствами:

Усеченная пирамида имеет два плоских многоугольных основания, которые могут быть различной формы, но параллельны друг другу.
В отличие от обычной пирамиды, усеченная пирамида может иметь наклонные боковые ребра, которые делают ее форму более сложной и необычной.
Усеченная пирамида может использоваться в качестве модели для создания архитектурных конструкций, таких как купола, шатры, крыши зданий и т.д.
Усеченные пирамиды используются в различных областях науки и техники, включая архитектуру, физику, инженерию, компьютерную графику и многие другие.
Усеченная пирамида может быть использована как основа для создания различных предметов декора и искусства, таких как светильники, вазы, канделябры и т.д.
Усеченная пирамида может быть использована для создания различных игрушек и головоломок, что делает ее интересной не только для учебных, но и для развлекательных целей.

❓Вопросы и ответы

Вот некоторые часто задаваемые вопросы и ответы, связанные с калькулятором объема усеченной пирамиды:

Что такое усеченная пирамида?

Усеченная пирамида — это геометрическая фигура, которая имеет два параллельных многоугольных основания и наклонные боковые грани.

Как рассчитать объем усеченной пирамиды?

Объем усеченной пирамиды можно вычислить с помощью специальной формулы: V = (1/3) * h * (S1 + S2 + sqrt(S1 * S2)), где h — высота усеченной пирамиды, S1 и S2 — площади оснований, sqrt — квадратный корень.

Как использовать калькулятор объема усеченной пирамиды?

Введите значения высоты усеченной пирамиды, площадей ее оснований и нажмите кнопку «Вычислить». Калькулятор автоматически рассчитает объем усеченной пирамиды для вас.

Какие единицы измерения используются при вычислении объема усеченной пирамиды?

Объем усеченной пирамиды может быть выражен в кубических единицах измерения, таких как кубические метры, кубические сантиметры, кубические дюймы и т.д.

Для чего можно использовать калькулятор объема усеченной пирамиды?

Калькулятор объема усеченной пирамиды может быть полезен в образовательных целях, а также для проектирования и расчета объема различных конструкций и изделий.

Похожие калькуляторы

Возможно вам пригодятся ещё несколько калькуляторов по данной теме:

Калькулятор площади шара (сферы). Рассчитайте онлайн площадь поверхности шарообразного объекта (сферы).
Площадь правильного шестиугольника: калькулятор. Рассчитайте площадь правильного (равностороннего) шестиугольника с помощью онлайн-калькулятора.
Калькулятор числа «e». Посмотрите онлайн нужное число знаков после запятой в числе «e» (Эйлера или Непера).
Площадь поверхности куба: калькулятор. Рассчитайте онлайн площадь поверхности куба по длине ребер, диагонали куба или диагоналям его сторон.
Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.

Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!

Есть что добавить?

Напишите своё мнение, комментарий или предложение.

Показать комментарии

Источник

ВИДЕОУРОК

Усечённой пирамидой ABCDA₁B₁C₁D₁ называется часть пирамиды SABCD, заключённая между её основанием и секущей плоскостью, параллельной основанию.

Основаниями усечённой пирамиды называются параллельные грани ABCD и A₁B₁C₁D₁ (ABCD – нижнее основание, A₁B₁C₁D₁– верхнее основание).

Высотой усечённой пирамиды называется отрезок прямой, перпендикулярный её основаниям и заключённый между их плоскостями.

Усечённая пирамида называется правильной, если её основания – правильные многоугольники и прямая, соединяющая центры оснований, перпендикулярна плоскости оснований.

Апофемою правильной усечённой пирамиды называют высоту её боковой грани.

Свойства усечённой пирамиды.

Основания – подобные многоугольники.

Боковые грани – трапеции.

Отношение высоты к высоте пирамиды, из которой она получена, равно отношению разности сторон одной грани к длине нижнего основания этой самой грани.

Поверхность усечённой пирамиды.

Площадь боковой поверхности усечённой пирамиды равна сумме площадей её боковых граней.

Полная поверхность усечённой пирамиды равна сумме площади боковой поверхности и площадей оснований.

Боковая поверхность правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.

где Р и Р₁ – периметры оснований, m – апофема усечённой пирамиды.

Правильная четырёхугольная усечённая пирамида.

Правильная треугольная усечённая пирамида.

Правильная шестиугольная усечённая пирамида.

ЗАДАЧА:

В правильной четырёхугольной усечённой пирамиде стороны оснований равны 5 и 11 дм, а диагональ пирамиды – 12 дм. Определите боковую поверхность пирамиды.

РЕШЕНИЕ:

В усечённой пирамиде  АС₁  имеем
А₁В₁ = В₁С₁ = С₁D₁ = D₁А₁ = 5 дм,
АВ = ВС = СD = DА = 11 дм  и
А₁С = 12 дм.
Найти  боковую поверхность.

Из вершины А₁ проведём А₁N ⊥ AB и А₁M ⊥ AC, тогда А₁N – апофема пирамиды.

Боковая поверхность

S_бок = ¹/₂ (P + P₁) × A₁N.

где P = 4AB = 44
дм, а

P₁ = 4A₁B₁ = 20
дм.
В квадратах АВСD и А₁В₁С₁D₁ по иіх сторонам определяем диагонали

АС = 11√͞͞͞͞͞2 (дм),
A₁С₁ =5√͞͞͞͞͞5 (дм).

Рассмотрев равнобедренную трапецию АА₁С₁С, находим

и соответственно

Тогда из прямоугольного ∆ А₁MC находим высоту пирамиды

Из равнобедренного прямоугольного ∆ AMN (∠ ANM = 90°), гипотенуза которого AM = 3√͞͞͞͞͞2 (дм), находим сторону

Апофему данной пирамиды найдём из прямоугольного

Подставляя найденные значения P, P₁ и A₁N в формулу боковой поверхности пирамиды, получим:

S_бок = ¹/₂ (44 + 20)×5 = 160 (дм²).

ОТВЕТ:

S = 160 дм² = 1,6 м².

ЗАДАЧА:

Высота правильной четырёхугольной усечённой пирамиды
равна 4
см. Стороны оснований равны 2
см и
8 см. Найдите площадь диагональных сечений.

РЕШЕНИЕ:

Начертим чертёж.

Диагональные сечения
AA₁C₁D и BB₁D₁D– равные равнобедренные трапеции с высотой ОО₁ = h = 4 см и с основаниями
– диагоналями оснований АС и А₁С₁ та ВD и В₁D₁ соответственно. ABCD – квадрат, а поэтому

AC² = AD² + CD² =

= 8² + 8² = 128,

AC = √͞͞͞͞͞128 = 8√͞͞͞͞͞2 (cм).

A₁B₁C₁D₁ – квадрат, а поэтому

A₁C₁² = A₁D₁² + C₁D₁² = 2² + 2² = 8,

A₁C₁ = √͞͞͞͞͞8 = 2√͞͞͞͞͞2 (cм).

ОТВЕТ: 20√͞͞͞͞͞2 (cм²)

ЗАДАЧА:

В правильной четырёхугольной усечённой пирамиде высота
равна 2
см, а стороны оснований – 3 см и 5
см. Найдите диагональ этой пирамиды.

РЕШЕНИЕ:

Начертим чертёж.

Диагональным сечением данной пирамиды
является равнобедренная трапеция АА₁С₁С.

Так как
А₁С₁ и АС –
диагонали квадратов, А₁В₁С₁D₁ и ABCD, то

А₁С₁= А₁В₁ ∙ √͞͞͞͞͞2 = 3√͞͞͞͞͞2 (см) и

АС= АВ ∙ √͞͞͞͞͞2 = 5√͞͞͞͞͞2 (см).

Проведём
А₁К ⊥
АС
и С₁Н ⊥ АС. Тогда А₁С₁НК – прямоугольник
и А₁С₁ =
КН. Так что, прямоугольные треугольники АА₁К и СС₁Н равны по гипотенузе и катету.

Тогда,

АК = СН = ¹/₂ (АС – А₁С₁) =

^= 1/₂ (5√͞͞͞͞͞2 – 3√͞͞͞͞͞2) = √͞͞͞͞͞2 (см).

Тогда,

СК = АС – АК = 5√͞͞͞͞͞2 – √͞͞͞͞͞2 =
4√͞͞͞͞͞2 (см),

и по
теореме Пифагора в ∆ А₁СК:

ОТВЕТ: 6 см

ЗАДАЧА:

В правильной четырёхугольной пирамиде плоскость, проведённая
параллельно основанию, делит высоту пирамиды пополам. Найдите сторону основания,
если площадь сечения равна 36 см².

РЕШЕНИЕ:

Пусть SABCD – данная правильная пирамида,

основание – квадрат
ABCD, SO – высота, O –
точка пресечения диагоналей квадрата, φ – плоскость сечения, О₁ –
точка пересечения φ и SO, φ ∥ (ABC), S = 36 cм².

Поскольку φ ∥ (ABC),
то прямые пересечения 𝜑 и боковых граней параллельны соответственно рёбрам
основания:

A₁B₁ ∥ AB, B₁C₁ ∥ BC, C₁D₁ ∥ CD,

A₁D₁ ∥ AD, 𝜑 ⊥ SO,

можно рассмотреть гомотетию с центром S и коэффициентом

которая преобразует квадрат ABCD в квадрат
А₁В₁С₁D₁, стороны которого в два раза меньше, а

S_ABCD = 4S_А_1В1С1D1 = 4 ∙ 36 (см²).

S_ABCD = a² = 4 ∙
36,

a = 2 ∙ 6
= 12 (см).

ОТВЕТ: 12 см

Задания к уроку 10

Задание 1
Задание 2
Задание 3

Другие уроки:

Урок 1. Прямые и плоскости в пространстве
Урок 2. Прямая призма
Урок 3. Наклонная призма
Урок 4. Правильная призма
Урок 5. Параллелепипед
Урок 6. Прямругольный параллелепипед
Урок 7. Куб
Урок 8. Пирамида
Урок 9. Правильная пирамида
Урок 11. Цилиндр
Урок 12. Вписанная и описанная призмы
Урок 13. Конус
Урок 14. Усечённый конус
Урок 15. Вписанная и описанная пирамиды
Урок 16. Сфера и шар
Урок 17. Комбинация тел

Источник

Усеченная пирамида – это многогранник, который образуется основанием пирамиды и параллельным ему сечением. Можно сказать, что усеченная пирамида – это пирамиду со срезанной верхушкой. Эта фигура обладает множеством уникальных свойств:

Боковые грани пирамиды являются трапециями;
Боковые ребра правильной усеченной пирамиды одинаковой длины и наклонены к основанию под одинаковым углом;
Основания являются подобными многоугольниками;
В правильной усеченной пирамиде, грани представляют собой одинаковые равнобедренные трапеции, площадь которых равна. Также они наклонены к основанию под одним углом.

Формула площади боковой поверхности усеченной пирамиды представляет собой сумму площадей ее сторон: ${S_b}=sum{i=1}{n}{S_i}$

Так как стороны усеченной пирамиды представляют собой трапеции, то для расчета параметров придется воспользоваться формулой площади трапеции. Для правильной усеченной пирамиды можно применить другую формулу расчета площади. Так как все ее стороны, грани, и углы при основании равны, то можно применить периметры основания и апофему, а также вывести площадь через угол при основании.

Если по условиям в правильной усеченной пирамиде даны апофема (высота боковой стороны) и длины сторон основания, то можно произвести расчет площади через полупроизведение суммы периметров оснований и апофемы:

$S={1/2}(P_1 + P_2) l$

Давайте рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.
Дана правильная пятиугольная пирамида. Апофема l = 5 см, длина грани в большом основании равна a = 6 см, а грань в меньшем основании b = 4 см. Рассчитайте площадь усеченной пирамиды.

Для начала найдем периметры оснований. Так как нам дана пятиугольная пирамида, мы понимаем, что основания представляют собой пятиугольники. Значит, в основаниях лежит фигура с пятью одинаковыми сторонами. Найдем периметр большего основания:

Таким же образом находим периметр меньшего основания:

Теперь можем рассчитывать площадь правильной усеченной пирамиды. Подставляем данные в формулу:
$S_{6ok}={1/2}*(30+20)*5=25*5=125 cm^2$
Таким образом, мы рассчитали площадь правильной усеченной пирамиды через периметры и апофему.

Еще один способ расчета площади боковой поверхности правильной пирамиды, это формула через углы у основания и площадь этих самых оснований.

$S_{6ok}={S_{1 OCH}-S_{2 OCH}}/{cos{beta}}$

Давайте рассмотрим пример расчета. Помним, что данная формула применяется только для правильной усеченной пирамиды.

Пусть дана правильная четырехугольная пирамида. Грань нижнего основания a = 6 см, а грань верхнего b = 4 см. Двухгранный угол при основании β = 60°. Найдите площадь боковой поверхности правильной усеченной пирамиды.

Для начала рассчитаем площадь оснований. Так как пирамида правильная, все грани оснований равны между собой. Учитывая, что в основании лежит четырехугольник, понимаем, что нужно будет рассчитать площадь квадрата. Она представляет собой произведение ширины на длину, но в квадрате эти значения совпадают. Найдем площадь большего основания:
$S_{1OCH}=6^2=36 cm^2$
$S_{2OCH}=4^2=16 cm^2$
Теперь используем найденные значения для расчета площади боковой поверхности.
$S_{6ok}= {36-16}/0.5 = 40 cm^2$

Зная несколько несложных формул, мы легко рассчитали площадь боковой трапеции усеченной пирамиды через различные значения.

Источник

Как найти площадь поверхности усеченной пирамиды

На данной странице калькулятор поможет рассчитать площадь поверхности пирамиды онлайн. Для расчета задайте периметры оснований и апофему.

Усеченная пирамида — многогранник, образованный пирамидой и её сечением, параллельным основанию.

Апофема – опущенный перпендикуляр из вершины на ребро основания.

Боковая поверхность через периметры и апофему

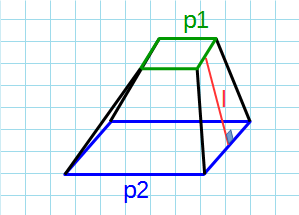
Формула площади боковой поверхности усеченной пирамиды через периметры и апофему:

p1 — периметр верхнего основания; p2 — периметр нижнего основания; l — апофема усеченной пирамиды.

Источник

Этот онлайн-калькулятор поможет узнать не только площадь усеченной пирамиды, но и 18 дополнительных значений. Для этого должны быть известны всего 4 значения, такие как: длины сторон верхнего и нижнего основания, общее количество граней, а также один показатель на выбор из следующих: длина ребра, высота, апофема или площадь боковой поверхности усеченной пирамиды. Введя все необходимые значения и нажав на кнопку расчета, можно будет узнать объем усеченной пирамиды, площадь, высоту, угол сторон основания, длину всех ребер и другие величины. Благодаря развернутым формулам в ответах разобраться в расчетах по величинам фигуры не составит труда.

Введите данные:

Сторона верхнего основания (a) *

Сторона нижнего основания (b) *

Количество граней усеченной пирамиды (n) *

Значение ключевого показателя *

Округление:

* — обязательно заполнить

Источник