Формулы объёма и площади поверхности. Многогранники.
Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:
- Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
- Элементарная логика.
Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.
 Куб |
|
|
 Параллелепипед |
|
|
 Прямоугольный параллелепипед |
|
|
 Призма |
|

|
 Пирамида |
|

|
Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».
Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.
Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.
Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.
Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.
Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Решение:
Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб 
Очевидно, их 6, поскольку у куба 6 граней.
Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.
Разберем задачи, где требуется найти площадь поверхности многогранника.
Мы рассмотрим призмы и пирамиды. Начнем с призмы.
Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.
Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.
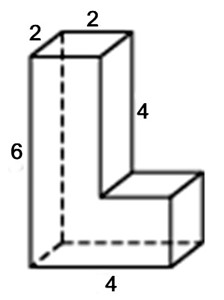
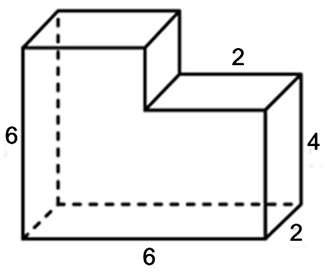
Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Многогранник на рисунке – это прямая призма с высотой 12.
Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:
(больший квадрат),
(маленький прямоугольник),
Подставим все данные в формулу: 
Ответ: 424.
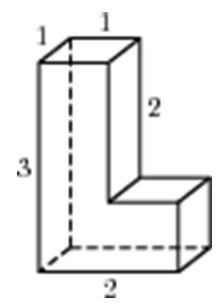
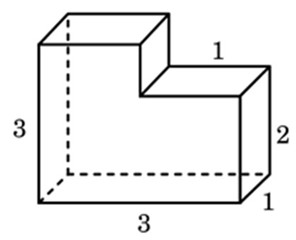
Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
Решение.
Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:
Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:
(большой прямоугольник),
(маленький прямоугольник).
Найдем площадь полной поверхности:
Ответ: 54
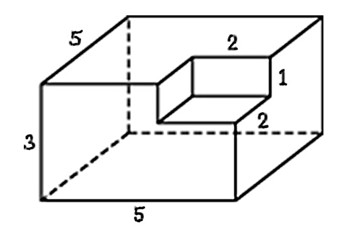
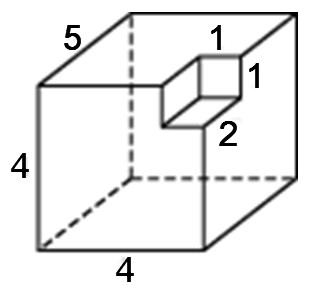
Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Покажем еще один способ решения задачи.
Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.
И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:
Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело. Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.
Ответ: 42
Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.
Решение.
Пусть АВ = 5 см, ВС = 3 см, тогда
Из по теореме косинусов найдем ребро АС:
Отрезок АС – большая сторона , следовательно,
большая боковая грань призмы.
Поэтому или
откуда
Ответ: 75
Теперь две задачи на площадь боковой поверхности пирамиды.
Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.
Решение.
Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.
Проведем , тогда
(по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.
– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.
Из прямоугольного получим:
Из прямоугольного имеем:
(по двум катетам), тогда
следовательно
Ответ: 192
Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.
Решение:
Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.
Площадь поверхности пирамиды равна
где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.
Значит, полупериметр основания .
Апофему найдем по теореме Пифагора:
Ответ: 2256
Как решать задачи на нахождение объема многогранника сложной формы?
Покажем два способа.
Первый способ
1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.
Второй способ.
1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.
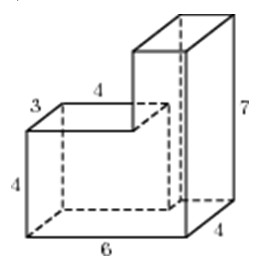
Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
1) Достроим составной многогранник до параллелепипеда.
2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:
3) Найдем объем лишней части, то есть маленького параллелепипеда.
Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем
4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:
Ответ: 220.
Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.
Объем призмы равен , а так как призма прямая, то ее боковое ребро является и высотой, то есть
Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания
Ответ: 126
Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.
Решение.
Объем призмы равен
Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.
Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.
Объем воды не изменился, Так как
высота воды
должна быть в 81 раз меньше, чем
Она равна
(см).
Ответ: 4
Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды
Решение.
Опустим из вершины высоту
Н на основание
Диагональ основания делит его на два равных треугольника, следовательно,
Имеем:
Ответ: 3,5
Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна
Решение.
По формуле объема пирамиды, 
В основании пирамиды лежит правильный треугольник. Его площадь равна
Объем пирамиды
Ответ: 96
Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.
Решение.
По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.
Пусть тогда
Так как точки М и К – середины АD и DС соответственно, то
Площадь треугольника MDK, лежащего в основании новой призмы, составляет часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен
Ответ: 4
Докажем полезную теорему.
Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
Доказательство:
Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.
Больше задач на формулы объема и площади поверхности здесь.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Площади и объемы многогранников
Что такое многогранник
Простейшей геометрической фигурой является прямая. Ею называется линия, которая имеет свое продолжение вправо и влево. Если эту прямую ограничить с двух сторон, получится отрезок. Для определения его величины достаточно одного измерения — длины. Прямая, ограниченная с одной стороны, имеет свое название. Это отрезок.
Источник: rusinfo.info
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В пределах одной плоскости, кроме прямой, которую можно измерить одной величиной, существуют геометрические фигуры, измеряемые длиной и шириной. Это многоугольники.
Источник: sun9-19.userapi.com
Они могут иметь различное количество углов и характеризуются таким понятием как площадь.
Фигура, которая располагается в нескольких плоскостях, характеризуется пространственными величинами или трехмерным измерением. К таким фигурам относят многогранники.
Многогранник — геометрическая фигура, имеющая замкнутую поверхность, которую можно представить совокупностью многоугольников.
Для полной характеристики многогранника необходимо назвать следующие свойства:
- стороны обязательно являются смежными с одной соседней стороной;
- при необходимости можно, начав движение от одного из многоугольников, достигнуть любого другого, используя принцип смежности;
- площадь поверхности многогранника равна сумме площадей многоугольников, ограничивающих фигуру.
При этом каждый многоугольник — это грань, сторона — ребро, а вершина — вершина многогранника.
Многогранник, как геометрическое тело, может быть представлен несколькими параллелепипедами, которые соединены по одной из граней. В таком случае их площадь будет равна сумме площадей свободных сторон и одной стороны, по которой произошло соединение. Объем такого тела будет равен сумме объемов каждого из параллелепипедов.
Источник: examer.ru
Многогранники бывают:
- выпуклыми (каждая из точек фигуры находится по одну сторону от плоскости);
- невыпуклыми (не все точки располагаются по одну сторону плоскости).
Проще говоря, выпуклый многогранник можно поставить на одну из сторон, и он будет на ней «уверенно стоять». С невыпуклым такого действия совершить нельзя.
Примечание 1
Важно помнить, что многогранник — это не только поверхность, состоящая из нескольких многоугольников. Это еще и тот внутренний объем, который ограничивает данная поверхность. Именно поэтому в стереометрии отделяют два понятия: площадь многогранника и его объем.
Как найти площадь: формулы
В зависимости от того, какой фигурой представлен многогранник, выбирают формулу для расчета площади его поверхности. Рассмотрим примеры.
1. Дана призма (многогранник, у которого в параллельных плоскостях расположены два многоугольника, являющихся гранями. Прочие грани представлены параллелограммами).
Источник: osiktakan.ru
Найти площадь данной фигуры можно следующим образом:
Источник: osiktakan.ru
2. Дан параллелепипед (один из вариантов призмы, все шесть граней которой являются параллелограммами).
Источник: osiktakan.ru
В этом случае S=2(ab+bc+ac)
3.Дана пирамида (вид многогранника с основанием в виде n-угольника и боковыми гранями по форме треугольниками. Обязательное условие: все треугольники имеют одну общую вершину, у которой есть свое название — вершина пирамиды).
Источник: osiktakan.ru
Площадь пирамиды можно найти по формуле:
Источник: osiktakan.ru
Примечание 2
Особый случай, когда у пирамиды нет вершины. Такая фигура носит название усеченной. Ее можно себе представить, если мысленно параллельно основанию провести сечение (см. рисунок).
Источник: osiktakan.ru
Sбок усеченной пирамиды находят по формуле:
Источник: osiktakan.ru
В стереометрии существует понятие правильного многогранника. Его вводят для фигур, у которых:
- все грани представлены правильными многоугольниками;
- число граней у всех углов идентично;
- ребра являются равными отрезками;
- величины плоских углов идентичны.
Перечисленным требованиям отвечают 5 видов многогранников, представленных в таблице:
| Наименование фигуры | Пример | |
| 1 | Правильный четырехгранник | Правильный тетраэдр |
| 2 | Правильный шестигранник | Куб |
| 3 | Правильный восьмигранник | Правильный октаэдр |
| 4 | Правильный двенадцатигранник | Правильный додекаэдр |
| 5 | Правильный двадцатигранник | Правильный икосаэдр |
Определить площадь правильных многогранников также несложно, зная следующие формулы (нумерация согласно строке таблицы):
1. S=a2√3
2. S=6a2
3. S=2a2√3
4.
Источник: osiktakan.ru
5. S=5a2√3
Использовать данный формулы нужно в задачах, требующих определить площадь поверхности многогранника, без учета его внутреннего объема.
Объем многогранника: формулы
Объем многогранника, в отличие от площади его поверхности, не может быть определен только касательно поверхности. Ведь он представляет собой все внутреннее пространство, которое ограничивается имеющейся поверхностью. На практике говорят, что объем является величиной, с помощью которой описывают размер трехмерных фигур. Эти фигуры так и называют: объемные (тела). У объемной фигуры имеется не только длина и ширина, но и высота – параметр, измеряемый в третьей плоскости.
Решить задачи по определению объема многогранника также можно с использованием формул.
Рассмотрим следующий рисунок:
Источник: interneturok.ru
Объем такого тела определяется по формуле:
V=a*b*c
Поскольку по рисунку видно, что a*b=S, а c является высотой (h), то формулу можно записать в виде: V=S*h
Рассмотренный вариант касается прямоугольного параллелепипеда. Если же произвольный параллелепипед имеет наклонные вертикальные грани, то данная формула также верна, однако проведенная высота отличается от бокового ребра, и, возможно, лежит внутри либо вне самого тела:
Источник: interneturok.ru
Формула определения объема через площадь и высоту подходит и для такого трехмерного тела, как призма (причем как для прямой, так и наклонной):
Источник: interneturok.ru
В быту часто происходит образование новых многогранников в процессе обрезания кусков от старых и приставления их к уже имеющимся. Как же вычислить объем такого геометрического тела? В геометрии используется принцип Кавальери. Суть его в следующем. Площади прямоугольника и параллелограмма равны потому что они в своей структуре имеют отрезки одинакового размера. Проще говоря, если представить рассечение обеих фигур плоскостями, параллельными основанию, величина отрезка слева всегда будет равна величине отрезка справа. Если третья фигура имеет такое же строение, по ее площадь будет такой же.
Источник: interneturok.ru
Объем многогранника, который может быть разделен на два и более многогранников, может определяться суммой их объемов.
Источник: image2.slideserve.com
Для систематизации формул, применяемых для определения объемов многогранников, рассмотрим таблицу:
| Наименование фигуры | Формула объема | |
| 1 | Параллелепипед непрямоугольный, призма | V=S*h |
| Параллелепипед прямоугольный | V=a*b*c | |
| 2 | Куб | V=a3 |
| 3 | Пирамида | S=1/3(Sh) |
На практике определить объем трехмерного тела можно и без формулы. Например, найти объем призмы можно, если умножить площадь ее основания на высоту фигуры. При этом вариант, когда в основании призмы лежит треугольник, предполагает, что нужно найти его площадь. Если основание квадрат, на первом этапе — нахождение площади квадрата. Величину высоты определяем, опуская перпендикуляр к основанию.
Примеры решения задач
Задача 1
Треугольник ABC — основание пирамиды DABC. При этом AC=AB=13см, BC=10см. AD=9см, это перпендикуляр к основанию. Найти S боковой поверхности.
Источник: ege-study.ru
Искомая величина равна сумме площадей боковых граней этой пирамиды.
Из вершин A и D проведем перпендикуляры к стороне BC. Тогда высота треугольника DBC — DK.
Треугольник ABC является равнобедренным, поскольку AB=AC. Тогда высота AK, которую провели по направлению основания BC, совпадает с медианой. Соответственно BK=KC=5см.
Источник: ege-study.ru
Ответ: 192 см3
Задача 2
Имеется выпуклый многогранник. У него 8 граней, в т.ч. 4 пятиугольника и 4 четырехугольника. Определить, сколько у данного тела ребер и вершин. Определим сумму всех граней: 4*4+4*5=36
Поскольку смежные ребра посчитаны дважды, найденное количество необходимо разделить на два: 36/2=18
В+Г-Р=2
В+12-30=2
В+12-2=30
В+10=30
В=20
Ответ: вершин — 20, ребер — 30.
Задача 3
Если переплавить три куба из латуни, у которых ребра равны соответственно 3, 4, 5см, в один куб, какая величина ребра получится у нового куба?
Решение.
Источник: famiredo.ru
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
24 мая
Обновлённая панель инструментов
22 мая
Беседы Решу ЕГЭ по подготовке к ЕГЭ
11 мая
Решение досрочных ЕГЭ по всем предметам
5 мая
Обновленный поиск заданий по ключевым словам
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Площадь поверхности составного многогранника
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 2 № 25541
i
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Аналоги к заданию № 25541: 25543 25549 25545 … Все
Решение
·
1 комментарий
·
Видеокурс
·
Помощь
2
Тип 2 № 25561
i
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Аналоги к заданию № 25561: 25563 25569 512372 … Все
Источник: ЕГЭ по математике 10.06.2013. Вторая волна. Центр. Вариант 601
Решение
·
Видеокурс
·
Помощь
3
Тип 2 № 25581
i
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Аналоги к заданию № 25581: 25583 25589 25585 … Все
Решение
·
1 комментарий
·
Видеокурс
·
Помощь
4
Тип 2 № 25601
i
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Аналоги к заданию № 25601: 25603 25609 505146 … Все
Решение
·
7 комментариев
·
Видеокурс
·
Помощь
5
Тип 2 № 25621
i
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Аналоги к заданию № 25621: 25623 25625 25629 … Все
Решение
·
3 комментария
·
Видеокурс
·
Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Площадь поверхности многогранника. В данной рубрике в опубликованных статьях «Общий обзор. Формулы стереометрии« и «Что ещё необходимо знать для решения по стереометрии« мы уже рассмотрели теоретические моменты, которые необходимы для решения.
В составе ЕГЭ по математике имеется целый ряд задач на определение площади поверхности и объема составных многогранников. Это, наверное, одни из самых простых задач по стереометрии. НО! Имеется нюанс. Не смотря на то, что сами вычисления просты, ошибку при решении такой задачи допустить очень легко.
В чём же дело? Далеко не все обладают хорошим пространственным мышлением, чтобы сразу увидеть все грани и параллелепипеды из которых «состоят» многогранники. Даже если вы умеете делать это очень хорошо, можете мысленно сделать такую разбивку, всё-таки следует не торопиться и воспользоваться рекомендациями из этой статьи.
Кстати, пока работал над данным материалом, нашёл ошибку в одной из задач на сайте. Нужна внимательность и ещё раз внимательность, вот так.
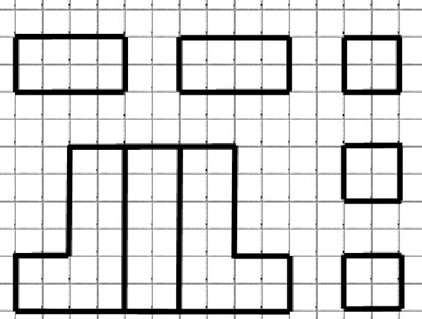
Итак, если стоит вопрос о площади поверхности, то на листе в клетку постройте все грани многогранника, обозначьте размеры. Далее внимательно вычисляйте сумму площадей всех полученных граней. Если будете предельно внимательны при построении и вычислении, то ошибка будет исключена.
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Используем оговоренный способ. Он нагляден. На листе в клетку строим все элементы (грани) в масштабе. Если длины рёбер будут большими, то просто подпишите их.
Ответ: 72
Решите самостоятельно:
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Посмотреть решение
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Посмотреть решение
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Посмотреть решение
Ещё задачи 25881, 77155, 77156. В них приведены решения другим способом (без построения), постарайтесь разобраться — что откуда взялось. Также решите уже представленным способом.
* * *
Если требуется найти объём составного многогранника. Разбиваем многогранник на составляющие его параллелепипеды, записываем внимательно длины их рёбер и вычисляем.
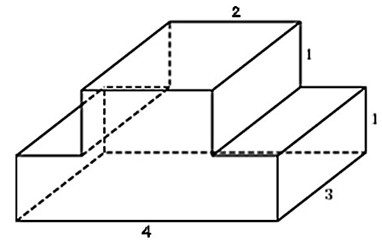
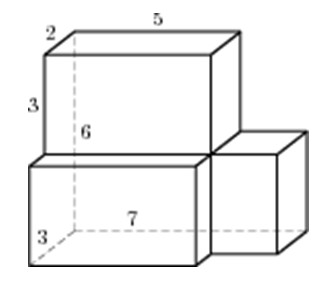
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Объем многогранника, изображенного на рисунке равен сумме объёмов двух многогранников с рёбрами 6,2,4 и 4,2,2
Ответ: 64
Решите самостоятельно:
Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).
Посмотреть решение
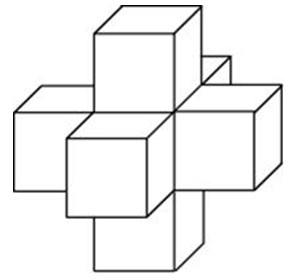
Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.
Посмотреть решение
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Посмотреть решение
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Посмотреть решение
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Посмотреть решение
Казалось бы, данные задачи можно вообще не рассматривать, они же просты и понятны. Но в их решении важна практика. Повторюсь, что ошибиться очень легко, попрактикуйтесь с подобными задачами и вы убедитесь.
В открытом банке задач много примеров аналогичных задач (смотрите здесь и здесь). Договоритесь с одноклассниками решить одни и те же задачи, затем сверьтесь.
Мы продолжим рассматривать задачи данной части, не пропустите! Успехов вам!!!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Такое задание можно выполнить несколькими способами:
а) Вычислить отдельные составляющие многогранника без достроения
б) Достроить до полноценной фигуры (параллелепипеда) и вычесть площадь поверхности фигуры, которую мы «приклеили» в изначально заданному многограннику
Воспользуемся первым способом:
Разметим поверхности для удобства как показано на рисунке и по отдельности вычислим площади составляющих общую поверхность поверхностей составляющих, после чего сложим полученные площади и получим ответ.
S1 = 1*2 = 2
Таких поверхностей у нас две => S1*2 = 2*2 = 4
S2 = 1*1 = 1
Аналогично, две поверхности => S2*2 = 1*2 = 2
S3 = 2*1 = 2
S4 = 1*2 = 2
Две поверхности => S4*2 = 2*2 = 4
S5 = 1*1 = 1
Аналогично, S5*2 = 1*2 = 2
S6 = 2*1 = 2, S6*2 = 2*2 = 4
Теперь сложим все площади: 4 + 2 + 2 + 4 + 2 + 4 = 18