План урока:
Площадь прямоугольного треугольника
Площадь произвольного треугольника
Площадь параллелограмма
Площадь ромба
Площадь трапеции
Площадь прямоугольного треугольника
Пусть в прямоугольном треугольнике известны два его катета. Обозначим их буквами а и b. Как тогда вычислить площадь такого треуг-ка?
Прямоугольный треугольник можно достроить до прямоугольника:
Площадь получившегося прямоугольника равна произведению чисел а и b. С другой стороны, прямоугольник состоит из двух треуг-ков площадью S, поэтому его общая площадь составляет 2S. Тогда можно записать, что
Задание. Катеты прямоугольного треугольника имеют длины 3 и 4. Определите его площадь.
Решение. Просто подставляем в формулу вместе букв a и b числа 3 и 4:
Задание. Площадь прямоугольного треугольника равна 100, а один катет больше другого вдвое. Найдите оба катета.
Решение. Пусть меньший катет равен х, тогда больший катет будет равен 2х. Выразим площадь прямоугольного треугольника через х:
Естественно, нас интересует только положительный корень, а отрицательный можно отбросить:
x = 10
Меньший катет оказался равным 10, тогда больший катет, который вдвое больше, будет равен 20.
Ответ: 10; 20.
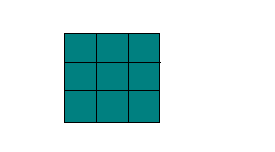
Задание. Найдите площадь фигуры, показанной на рисунке. Сторона каждой клеточки имеет длину, равную единице:
Решение. Эту фигуру можно разбить на квадрат со стороной 8 и два прямоугольных треуг-ка, то есть всего на три фигуры:
Подсчитаем площадь каждой из трех фигур по отдельности:
Чтобы найти площадь всей фигуры, достаточно просто сложить три полученных числа:
Задание. Вычислите площадь треуг-ка, изображенного на рисунке (площадь каждой отдельной клеточки составляет единицу):
Решение. Здесь проблема заключается в том, что треуг-к прямоугольным не является. Однако можно построить прямоуг-к, который будет состоять сразу из 4 треуг-ков:
Мы можем найти как площадь всего прямоугольника (обозначим ее как S), так и площади трех прямоугольных треуг-ков S1, S2 и S3:
Площадь произвольного треугольника
Перейдем к более сложному случаю, когда необходимо подсчитать площадь произвольного треугольника, не являющегося прямоугольным. Предположим, надо найти площадь произвольного ∆АВС. Опустим из А на сторону ВС высоту АН:
В результате мы получили два прямоугольных треуг-ка, ∆АВН и ∆АCН. Мы уже знаем, как найти их площади:
Общая площадь всего ∆АВС равна сумме площадей ∆АВН и ∆АСН. Запишем ее и вынесем общий множитель АН/2 за скобки:
В скобках стоит сумма ВН + НС. Но ведь эта сумма равна длине стороны ВС! Тогда окончательно формулу можно записать в виде:
Получили, что для вычисления площади произвольного треугольника надо сначала умножить его высоту на сторону, на которую она падает, а далее поделить результат на 2. Однако для полного доказательства этого факта надо рассмотреть особый случай, когда высота в треуг-ке падает не на сторону, а на ее продолжение (такая ситуация возникает в тупоугольном треуг-ке):
На рисунке снова получились всё те же прямоугольные треуг-ки ∆АСН и ∆АВН. Запишем формулы их площади:
Отличие в том, что на этот раз площадь АВС можно вычислить не как сумму, а как разницу этих площадей:
Итак, можно сформулировать следующее правило:
Примечание. Часто сторону, на которую опущена высота, называют основанием треуг-ка.
Задание. Вычислите площадь ∆АВС, если сторона АВ имеет длину 7, а высота СН равна 4.
Решение. В данной задаче на сторону длиной 7 падает высота длиной 4. Надо просто подставить эти числа в формулу:
Задание. Докажите, что медиана треуг-ка разбивает его на два равновеликих треуг-ка.
Решение.
Пусть в ∆АВС проведена медиана СМ. Требуется доказать, что
Важно заметить, что СН будет являться высотой не только для ∆АВС, но также и для ∆СВМ и ∆САМ. Обозначим СН как h, а АВ как а. Тогда мы можем найти длины отрезков ВМ и АМ, ведь медиана делит сторону АВ пополам:
Получили одно и то же значение, то есть площади треуг-ков равны.
В рассмотренной задаче мы использовали тот факт, что у нескольких треуг-ков может быть общая высота. Общая высота используется и в многих других геометрических задачах.
Задание. Предложите способ, как разделить треуг-к, показанный на рисунке, на три равновеликих треуг-ка:
Чтобы треуг-ки были равновелики, достаточно, чтобы у них была общая высота, а основания, на которые эта высота падает, были бы равны друг другу. Поэтому можно просто поделить нижнюю сторону на три одинаковых отрезка (длиной по 7 клеток) и соединить концы полученных отрезков с противоположной вершиной:
Красной линией здесь показаны границы треуг-ков, а штриховой – их общая высота СН. Вычислить площадь каждого из треуг-ков можно по следующим формулам:
Но отрезки BD, DE и EA одинаковы (по 7 клеточек), поэтому одинаковы будут и площади:
Заметим, что необязательно делить на три одинаковых отрезка именно нижнюю сторону. Допустимы и два других варианта решения:
Но и это не единственные решения задачи. Попробуйте самостоятельно предложить ещё несколько вариантов.
Формула площади треуг-ка показывает, что между длинами высот и сторон есть взаимосвязь.
Задание.В ∆РЕТ РЕ = 72, ЕТ = 45. Высота ТН имеет длину 40. Найдите высоту РМ.
Решение.
Зная ТН и РЕ, мы сможем найти площадь треуг-ка:
Теперь запишем эту формулу площади в ином виде, когда используется высота МР и сторона ЕТ
Величину SРЕТ мы только что вычислили, а длина ЕТ известна из условия, поэтому можно подставить их в формулу:
Площадь параллелограмма
Для вычисления площади параллелограмма введем понятие «высота параллелограмма». Так называют перпендикуляр, опущенный на сторону параллелограмма (ее в такой ситуации часто называют основанием) из одной из вершин параллелограмма. Важно понимать, что высоты могут упасть не на само основание, а на его продолжение. Так как у каждого параллелограмма есть 4 вершины, а из каждой из них можно опустить высоту на две противоположных вершины, то всего у параллелограмма должно быть 8 высот:
На рисунке синим показаны высоты параллелограмма, а красным цветом отмечены продолжения оснований. Оказывается, что площадь параллелограмма равна произведению его высоты и основания, на которую она опущена. Докажем это.
Опустим в параллелограмме АВСD высоты ВН и СК:
В результате получили четырехуг-к ВНКС, который является прямоугольником, ведь все его углы прямые. Очевидно, что ∆АВН и ∆DCK равные. Это можно доказать тем, что они являются прямоугольными, у них есть одинаковые гипотенузы АВ и CD (они равны как противоположные стороны параллелограмма) и одинаковые катеты ВН и СК (это уже противоположные стороны прямоугольника ВНКС).
Раз они равны, то одинаковы и их площади:
Но величину S3 можно заменить на S2. В свою очередь полученная сумма равна площади прямоугольника ВНКС, которая может быть вычислена как произведение его смежных сторон:
Но ВН – это высота, а НК – основание параллелограмма. То есть мы доказали следующее утверждение:
Задание. Найдите площадь параллелограмма, изображенного на рисунке:
Решение. По рисунке несложно определить длину как основания, так и высоты параллелограмма:
Далее надо просто перемножить эти длины:
Примечание. Конечно, если вы вдруг забыли формулу площади параллелограмма, можно просто разделить его на прямоугольник и два прямоугольных треуг-ка:
Дальше можно просто посчитать по отдельности S1, S2и S3, после чего сложить их. Попробуйте сделать это самостоятельно.
Задание. Площадь параллелограмма равна 162 см2, а одна из его высот вдвое короче основания, к которому она проведена. Найдите эту высоту и основание.
Решение. В данной задаче не потребуется даже рисунок. Обозначим высоту буквой h, тогда основание, которое вдвое длиннее, составляет 2h. Произведение этих чисел – это площадь, то есть оно равно 162:
Высота равна 9, а основание будет вдвое больше, то есть его длина равна 18.
Ответ: 9 и 18.
Задание. Смежные стороны параллелограмма ABCD имеют длину 12 и 14 см, а угол между ними равен 30°. Вычислите его площадь.
Решение. Опустим на сторону длиной 14 см высоту:
Для вычисления площади надо сначала найти высоту ВН. Её можно определить из ∆АВН. Он является прямоугольным, а его острый угол∠А = 30°. У такого треуг-ка катет, лежащий против 30°, вдвое меньше АВ:
Площадь ромба
Многие четырехуг-ки, изученные нами ранее, являются частными случаями параллелограмма. Для прямоугольника и квадрата мы уже знаем формулы вычисления площади. Осталось разобраться с ромбом. Ясно, что его площадь можно найти также, как и у параллелограмма. Однако площадь ромба можно посчитать и зная только его диагонали.
Построим ромб и проведем в нем диагонали:
Нам уже известно, что диагонали ромба пересекаются под прямым углом, а точка их пересечения является серединой для каждой диагонали:
Получается, что диагонали разбивают ромб на 4 одинаковых прямоугольных треуг-ка. Высчитаем, к примеру, SAOB:
В результате мы доказали следующее утверждение:
Задание. Одна диагональ ромба равна 3,2 дм, а другая составляет 14 см. Найдите его площадь.
Решение. Для начала надо перевести все длины в одинаковые единицы измерения. Заменим дециметры на сантиметры:
Задание. Одна диагональ ромба в три раза длиннее другой, а площадь фигуры составляет 150. Вычислите длину диагоналей ромба.
Решение. Обозначим меньшую диагональ как х, тогда вторая будет равна 3х. Выразим площадь через х:
Вторая диагональ ромба будет втрое длиннее, то есть ее длина равна 3•10 = 30
Ответ: 10 и 30 см.
Площадь трапеции
Осталось рассмотреть единственный известный нам вид четырехуг-ка, который не является параллелограммом. Это трапеция. Для вычисления ее площади также потребуется высота. Под ней подразумевают перпендикуляр, опущенный из вершины трапеции на одно из ее оснований. Другими словами, высота трапеции – это расстояние между основаниями трапеции.
В произвольной трапеции ABCD, где АD – большее основание, опустим из В высоту (то есть перпендикуляр) на AD, а из D– высоту на ВС. Также проведем диагональ ВD:
Ясно, что общая площадь трапеции будет равна сумме площадей ∆АВDи ∆ВСD. В свою очередь площадь каждого из них можно подсчитать по стороне и опущенной на нее высоте. Высоты мы как раз и провели, это ВН и DK, поэтому можно записать:
Теперь заметим, что отрезки ВН и КD одинаковы, ведь фигура ВНDК является прямоугольником. Тогда площадь ∆ВСD можно записать в таком виде:
В итоге мы доказали, что для вычисления площади трапеции следует ее высоту умножить на сумму длин оснований, после чего поделить результат на два. Обычно этот факт записывают следующим образом:
Задание. У трапеции АВСD основаниями являются АВ (21 см) и CD (17 см). Высота ВН составляет 7 см. Найдите площадь трапеции.
Решение. Это простая задача на использование формулы площади трапеции:
Задание. Найдите площадь прямоугольной трапеции, показанной на рисунке (площадь клеточки равна единице):
Решение. На рисунке показана прямоугольная трапеция. Её высота равна длине ее правой боковой стороны трапеции. Покажем размеры, необходимые нам для выполнения расчета:
Считаем площадь:
Задание. Тупой угол равнобедренной трапеции составляет 135°. Проведенная из этого угла высота делит противолежащее основание на отрезки длиной 14 и 34 см. Какова площадь трапеции?
Решение. Выполним построение:
Найдем острый угол трапеции. Так как CD||АВ, то
Рассмотрим ∆АDH. Он прямоугольный, а один из его острых углов равен 45°. Тогда и второй острый угол также равен 45°. То есть это равнобедренный треуг-к. Это помогает найти длину высоты DH:
ведь это прямоугольныетреуг-ки с равными гипотенузой и катетом:
Из равенства треуг-ков следует, что
Итак, сегодня мы узнали, как вычислять площади треуг-ков и некоторых видов четырехуг-ков. В большинстве случаев предварительно необходимо найти высоту в многоугольнике. В будущем мы узнаем ещё несколько формул для вычисления площадей фигур.
Цели:
- обучающие: научить учащихся находить площадь
многоугольника, используя выбранные ими способы,
сформировать начальные представления - многоугольнике, графические и измерительные
навыки; - развивающие: развитие способов умственной
деятельности учащихся при выполнении заданий от
наблюдения, расчетов до выяснения
закономерностей вычисления площади
многоугольника; - воспитывающие: раскрытие субъективного опыта
учащихся, поощрение действий, стремлений
учащихся как основы воспитания положительных
качеств личности; - методическая: создание условий для проявления
познавательной активности учащихся.
Оснащение урока:
- Оформление доски: слева — фигуры многоугольника,
справа — чистое полотно доски для записи на уроке,
в центре – многоугольник-прямоугольник. - Листок “К исследованию”.
- Инструментарии учителя и учащихся (мел, указка,
линейка, листок исследования, фигуры, ватман,
маркер).
Метод урока:
- По взаимодействию учителя и учащихся –
диалог-общение; - По способу решения задач – частично-поисковый;
- По способу умственной деятельности — (СУД)
развивающее обучение.
Форма урока — фронтальная, в парах,
индивидуальная.
Тип урока — урок усвоения новых знаний, умений и
навыков.
Структура урока — постепенное углубление в
тему, гибкая, диалогическая.
Ход урока
Приветствие.
Урок прекрасен и приносит радость, когда мы
мыслим, дружно работаем. Сегодня мы будем
рассматривать фигуры, определять их названия,
думать, искать и находить решения. Пожелаем друг
другу успешной работы.
Актуализация знаний.
Рассмотрите фигуры (на доске многоугольники).
Они все вместе. Почему? Какой у них общий
признак? (Многоугольники).
Назовите этот многоугольник (5-угольник,
6-угольник…)
Может быть, вы знаете, что такое площадь
многоугольника?
Тогда покажите на одной из фигур.
(Обобщение учителем: площадь — часть плоскости
внутри замкнутой геометрической фигуры.)
В русском языке это слово имеет несколько
значений.
(Ученик по словарю знакомит со значениями.)
- Часть плоскости внутри замкнутой
геометрической фигуры. - Большое незастроенное и ровное место.
- Помещение для какой-либо цели.
Какое из значений используется в математике?
В математике используется первое значение.
(На доске фигура).
Это многоугольник? Да.
Назовите фигуру по-другому. Прямоугольник.
Покажи длину, ширину.
Как найти площадь многоугольника?
Запишите при помощи букв и знаков формулу.
S = а * в
Если длина нашего прямоугольника 20 см, ширина
10см. Чему равна площадь?
Площадь равна 200 см2
Подумайте, как приложить линейку, чтобы фигура
разделилась на:
- Два треугольника
- Два четырехугольника
- Треугольник и четырехугольник
- Треугольник и пятиугольник
Увидели, из каких частей состоит фигура? А
теперь, наоборот, по частям соберем целое.
( Части фигуры лежат на партах. Дети собирают из
них прямоугольник ).
Сделайте вывод по наблюдениям.
Целую фигуру можно разделить на части и из
частей составить целую.
Дома на основе треугольников и
четырехугольников составляли фигуры, силуэты.
Вот какие они получились.
(Демонстрация рисунков, выполненных дома
учащимися. Одна из работ анализируется).
Какие фигуры использовал? У тебя получился
сложный многоугольник.
Постановка учебной задачи.
На уроке мы должны ответить на вопрос: как найти
площадь сложного многоугольника?
Для чего человеку нужно находить площадь?
(Ответы детей и обобщение учителем).
Задача определения площади возникла из
практики.
(Показывается план школьного участка).
Для того чтобы построить школу, сначала создали
план. Потом разбивалась территория на участки
определенной площади, размещались строения,
клумбы, стадион. При этом участок имеет
определенную форму — форму многоугольника.
Решение учебной задачи.
(Раздаются листы для исследования).
Перед вами фигура. Назовите ее.
Многоугольник, шестиугольник.
Найдем площадь многоугольника. Что для этого
надо делать?
Разделить на прямоугольники.
(При затруднении будет другой вопрос: “Из каких
фигур состоит многоугольник?”).
Из двух прямоугольников.
С помощью линейки и карандаша разделите фигуру
на прямоугольники. Обозначьте цифрами 1 и 2
полученные части.
Проведем измерения.
Найдем площадь первой фигуры.
(Учащиеся предлагают следующие варианты
решений и записывают их на доске).
1способ:
- S1 = 5 ? 2 = 10 см2
- S2 = 5 ? 1 = 5 см2
Зная площадь частей, как найти площадь целой
фигуры?
S = 10 + 5 = 15 см2
2 способ:
- S1 = 6 ? 2 = 12 см2
- S2 = 3 ? 1 = 3 см2
- S = 12 + 3 = 15 см2.
Сравните результаты и сделайте вывод.
Проследим наши действия
Как находили площадь многоугольника?
Составляется и записывается на плакате
алгоритм:?
1. Делим фигуру на части
2. Находим площади частей этих многоугольников (
S1, S2 ).
3. Находим площадь целого многоугольника ( S1
+ S 2 ).
Проговорить алгоритм.
( Несколько учащихся проговаривают алгоритм).
Мы нашли два способа, а может, есть еще?
А можно фигуру достроить.
Сколько прямоугольников получилось?
Два.
Обозначим части 1 и 2. Проведем измерения.
Найдите площадь каждой части многоугольника.
- S1=6? 5=30см2
- S2= 5 ? 3 = 15 см2
Как найти площадь нашего шестиугольника?
S = 30 – 15 = 15 см2
Составим алгоритм:
Достроили фигуру до прямоугольника
Нашли S1 и S2.
Нашли разность S1 – S2.
Сравните два алгоритма. Сделайте вывод. Какие
действия одинаковые? Где разошлись наши
действия?
Закройте глазки, опустите головки. Мысленно
повторите алгоритм.
Мы провели исследовательскую работу,
рассмотрели разные способы и теперь можем
находить площадь любого многоугольника.
Проверка результативности.
Проверьте себя.
Перед вами многоугольники.
Найти площадь одной фигуры по выбору, при этом
можете пользоваться разными способами.
Работа выполняется самостоятельно. Дети
выбирают фигуру. Находят площадь одним из
способов. Проверка – ключ на доске.
Что можно сказать о форме? ( Форма разная)
А какова площадь этих многоугольников? (
Площади этих многоугольников равны)
Оценивают результаты.
У кого правильно – поставь “+”.
У кого сомнения, затруднения – “?”
Консультанты оказывают помощь ребятам, ищут
ошибки, помогают исправить.
Домашнее задание:
Составить свои листки исследования, вычислить
площадь многоугольника разными способами.
Итог урока.
Итак, ребята, что вы расскажите родителям, о том
как найти площадь геометрической фигуры –
многоугольника.
Многоугольником считается фигура,имеющая количество сторон больше или равное 3.
1)Площадь треугольника со сторонами a,b,c, и высотами h1,h2,h3,
площадь S =a*h1/2=b*h2/2=c*h3/2,
или по формуле Герона :
S= V p*(p-a)*(p-b)*(p-c),
где p — полупериметр.
Площадь четырехугольника:
1)площадь квадрата :S = a^2,
2)площадь прямоугольника :S = a *b,
3)площадь параллелограмма : S =a * h1 = b *h2,
4)площадь ромба S = a *h =d1*d2,
где a,b -стороны четырёхугольника,h1,h2-высоты,d1,d2-диагонали ромба.
5)площадь произвольного четырёхугольника определяется путем разбивки его по диагонали и нахождения площади каждого треугольника отдельно.
Площадь правильного многоугольника равна произведению полупериметра =n*a,на апофему h
S=(n*a)*h/2
где а-сторона многоугольника,n-число сторон,h-апофема.
Для решения задач на нахождения периметра и площади прямоугольников и квадратов необходимо освоить следующие основные формулы:
a — длина
b — ширина
P — периметр
S — площадь
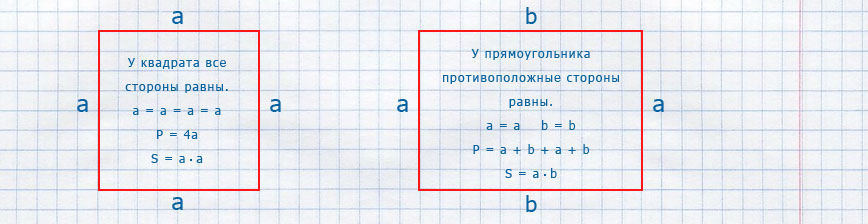
Формулы площади и периметра для квадрата
P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата
Формулы площади и периметра для прямоугольника
P = a + b + a + b; P = 2a + 2b;
P = (a + b) · 2 — периметр прямоугольника
S = a · b — площадь прямоугольника
Примеры решения задач разной сложности на нахождение периметра и площади
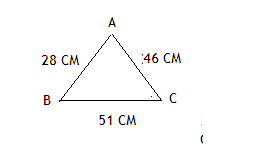
Задача 1
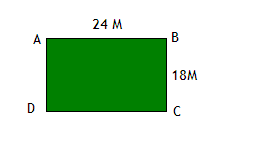
Каков периметр треугольника ABC?
Ответ: периметр треугольника равен 125 см.
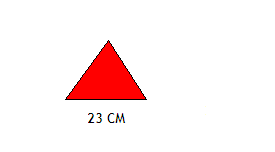
Задача 2
Красный треугольник является равносторонним со стороной 23 сантиметров. Чему равен его периметр?
Ответ: Все три стороны равностороннего треугольника равны. Таким образом, его периметр равен 23 · 3 = 69 см.
Задача 3
Равнобедренный треугольник имеет периметр 37 сантиметров, а его основание имеет длину 9 сантиметров. Каждая из двух других сторон будет иметь длину _____ см.?
Ответ: Равнобедренный треугольник имеет две равные стороны. Сумма равных сторон будет 37 — 9 = 28 см. Значит, каждая из них будет равна 28 : 2 = 14 см.
Задача 4
У Тимы есть сад в форме квадрата со стороной 9 метров. Какова длина забора, который опоясывает сад?
Ответ: Все стороны квадрата равны. Длина забора P равна длине стороны умноженной на 4. P = 4 · 9 = 36 метров.
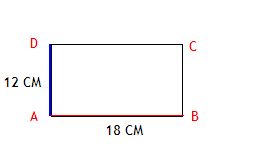
Задача 5
В прямоугольнике ABCD красная сторона составляет 18 см, а синяя сторона 12 см. Чему равен периметр прямоугольника?
Ответ: Периметр прямоугольника равен 60 см.
Задача 6
Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?
Ответ: Площадь прямоугольника 56 м².
Задача 7
Площадь витрины квадратной формы 64м². Узнай ее периметр.
Ответ: Периметр витрины равен 32 м.
Задача 8
Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.
Ответ: Площадь прямоугольника равна 630 см².
Задача 9
Парк имеет форму прямоугольника с длиной 24 метра и шириной 18 метров. Если на его сторонах надо посадить деревья с отступом в 2 метра друг от друга, то сколько нужно деревьев?
Ответ: 42 дерева.
Задача 10
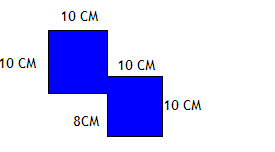
Каков периметр синей фигуры?
Ответ: Здесь есть два квадрата, у которых есть общая часть стороны. Так как сторона квадрата равна 10 см и часть стороны равна 8 см, то общая часть 2 см, а оставшаяся часть второго квадрата равна 8 см.
Периметр равен 10 + 10 + 8 + 10 + 10 + 10 + 8 + 10 = 76 см.
Задача 11
Два прямоугольных участка имеют одинаковую площадь. Длина первого — 48 м, а ширина 30 м. Чему равна длина второго участка, если его ширина на 6 м больше ширины первого участка?
Ответ: Длина второго участка 40 м.
Задача 12
Найди периметр квадрата со стороной 8 см.
Ответ: Периметр квадрата 32 см.
Задача 13
Сторона квадрата 6 см. Найди длину прямоугольника с таким же периметром и шириной 3 см.
Решение:
6 · 4 = 24 (см) -находим периметр квадрата
3 + 3 = 6 (см) -сумма ширины прямоугольника
24 — 6 = 18 (см)- сумма двух длин прямоугольника
18 : 2 = 9 (см)
Ответ: Длина прямоугольника 9 см.
Задача 14
Длина бассейна прямоугольной формы 15 м. Найди периметр бассейна, если его площадь 120 м2.
Решение:
120:15=8 (м)- ширина бассейна
(8+15)·2= 46 (м)
Ответ: Периметр бассейна 46 метров
Задача 15
Периметр квадрата 8 см. Из трех таких квадратов сложили прямоугольник. Найди периметр получившегося прямоугольника.
Решение:
8:4=2 (см)- сторона квадрата
2+2+2+2+2+2+2+2=16(см)
Ответ: Периметр прямоугольника 16 см.
Задача 16
Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см. На сколько см² он ошибся?
Решение:
5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 — 45 = 3 (см²)
Ответ: Ученик ошибся на 3 см²
Задача 17
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.
Решение:
4·2=8 (дм) -длина окна
8·4=32 (дм²)
Ответ: Площадь окна 32 дм²
Задача 18
Один прямоугольный участок имеет длину 36 м, а ширину 20 м. Найдите ширину другого участка с такой же площадью, если его длина на 6 м меньше длины первого участка.
Ответ: Ширина другого участка 24 м.
Задача 19
У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?
Ответ: Площадь квадрата больше на 4 см.
Задача 20
Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
Ответ: Площадь квадрата 36 см², периметр квадрата 24 см.
Задача 21
У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
Ответ: Площадь прямоугольника 35 м², периметр прямоугольника 24 см.
Задача 22
Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?
Решение:
1) 8 ∙ 8 = 64 (площадь клумбы)
2) 64 : 16 = 4(1/16 клумбы)
3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
4) 64 – 28 = 36
Ответ: Незабудками засажено 36 м².
Задача 23
Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?
Решение:
1) 6 ∙ 2 = 12
2) 18 – 12 = 6
3) 6 : 2 = 3 (ширина прямоугольника)
4) 3 ∙ 6 = 18
Ответ: Площадь прямоугольника 18 м².
Задача 24
Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?
Решение:
1) 4800 : 60 = 80 (длина стола)
2) 60 ∙ 2 = 120 см
3) 80 ∙ 2 = 160 см
4) 120 + 160 = 280 см
Ответ: Периметр стола 280 см.
Задача 25
Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?
Решение:
1) 5 ∙ 2 = 10
2) 40 – 10 = 30
3) 30 : 2 = 15 (другая сторона прямоугольника)
4) 5 ∙ 15 = 75
Ответ: Площадь прямоугольника 75 см².
Задача 26
Площадь квадрата 49 кВ дм. Узнайте его периметр.
Решение:
1) 49 : 7 = 7 (сторона квадрата)
2) 7 ∙ 4 = 28 (периметр квадрата)
Ответ: Периметр квадрата равен 28 дм.
Задача 27
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.
Решение:
1) 4 ∙ 2 = 8 (длина окна)
2) 4 ∙ 8 = 32
Ответ: Площадь окна равна 32 м².
Задача 28
Длина участка земли 54 м. ширина — 48 м. 5/9 площади засажено картофелем. Остальная часть участка – капустой. Какая площадь засажена капустой?
Решение:
1) 54 ∙ 48 = 2592 (площадь участка земли)
2) 2592 : 9 = 288 (1/9 площади)
3) 288 ∙ 5 = 1440 (5/9 площади)
4) 2592 – 1440 = 1152
Ответ: Капустой засадили 1152 м².
Задача 29
Найди периметр квадрата со стороной 16 см.
Ответ: Периметр квадрата 64 см.
Задача 30
Найди длину прямоугольника с помощью уравнения, если его ширина 7 см, а периметр равен 40 см.
Решение:
P = (a + b) · 2 — периметр прямоугольника
или
(a + b) · 2 = P,
где a — длина = ?, b — ширина = 7 см, P — периметр = 40 см.
Составим уравнение:
(а + 7) · 2 = 40
2а + 14 = 40
2а = 40 — 14
2а = 26
а = 26 : 2
а = 13
Ответ: Длина прямоугольника 13 см.
Задача 31
Найди ширину прямоугольника, если его длина 10 см, а периметр равен 30 см.
Ответ: Ширина прямоугольника 5 см.
Задача 32
Периметр квадрата 24 см. Найди его площадь.
Решение:
24 : 4 = 6 (см)
6 · 6 = 36 (см²)
Ответ: Площадь квадрата 36 см².
Задача 33
Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.
Ответ: Площадь прямоугольника 56 см².
Задача 34
Площадь прямоугольника 40 см². Ширина его 4 см. Чему равен периметр прямоугольника?
Решение:
40 : 4 = 10 (см)
(10 + 4) · 2 = 28 (см)
Ответ: Периметр прямоугольника 28 см.
Задача 35
Ребро куба равно 2 сантиметров. Найти площадь всех граней куба.
Решение:
Куб — многогранник, поверхность которого состоит из шести одинаковых по площади квадратов.
У куба 8 вершин, 12 рёбер, 6 граней (поверхностей).
Если S = a · a — площадь квадрата, тогда
S = (a · a) · 6 — площадь всех граней куба, из условия задачи a = 2, тогда S = 2 · 2 · 6
2 · 2 · 6 = 24 (см²)
Ответ: Площадь всех граней куба равна 24 см².
Задача 36
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Ответ: Площадь получившейся фигуры равна 44.
Задача 37
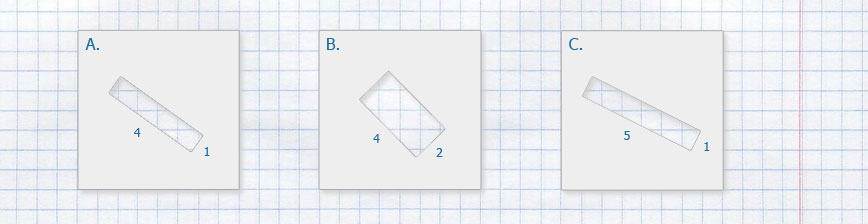
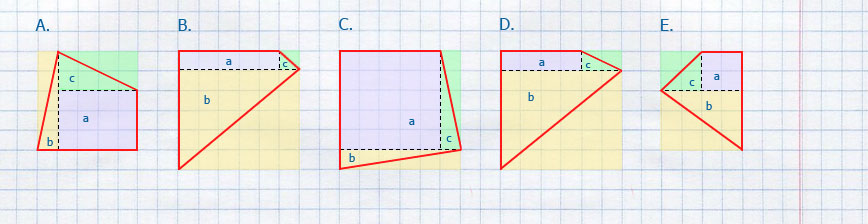
Площадь одной клетки равна 1см.
- Найдите площадь фигуры, изображённой на рисунке A.
- Найдите площадь фигуры, изображённой на рисунке B.
- Найдите площадь фигуры, изображённой на рисунке C.
- Найдите площадь фигуры, изображённой на рисунке D.
- Найдите площадь фигуры, изображённой на рисунке E.
Ответ: Площадь фигуры A 18,5 см², площадь фигуры B 20,5 см², площадь фигуры C 30,5 см², площадь фигуры A 18,5 см², площадь фигуры E 12 см².
Задача 38
Найдите площади и периметры фигурок. Сделайте вывод.
Ответ: Пусть каждая из сторон клетки равна 1 см, тогда применив формулу площади квадрата S = a · a получим площадь одной клетки 1 · 1 = 1 см²
Фигура A — прямоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура A имеет четыре стороны, тогда 1 + 4 + 1 + 4 = 10 см — периметр фигуры.
Фигура B — квадрат состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура B имеет четыре стороны, тогда 2 + 2 + 2 + 2 = 8 см — периметр фигуры.
Фигура C — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура C имеет шесть сторон, тогда 3 + 1 + 2 + 1 + 2 + 1 = 10 см — периметр фигуры.
Фигура D — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура D имеет восемь сторон, тогда 1 + 1 + 2 + 1 + 1 + 1 + 2 + 1 = 10 см — периметр фигуры.
Фигура E — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура E имеет восемь сторон, тогда 1 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 10 см — периметр фигуры.
Вывод: Фигуры A, B, C, D, E имеют одинаковую площадь, но наименьший периметр имеет квадрат. У разных по форме плоских фигур, с одинаковой площадью, наименьший периметр всегда имеет квадрат.
Задача 39
Квадрат в данной фигуре имеет периметр 24 см. Синий треугольник — периметр 15 см. Каков периметр красной фигуры?
Ответ: Периметр красной фигуры равен 27 см.
Задача 40
Периметр каждого из зеленых квадратов 12 см. Каков периметр большого квадрата?
Ответ: Периметр равен 36 см.
Задача 41
Площадь прямоугольника 72 см2. Какова длина и ширина прямоугольника, если ширина в 2 раза меньше, чем его длина?
Ответ: Длина прямоугольника равна 12 см. а ширина — 6 см.
Задача 42
Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (катет) b = 8 см.
Ответ: Периметр прямоугольника равен 24 см.
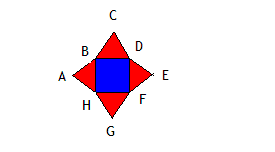
Задача 43
Периметр красного квадрата равен 16см. Красные треугольники равносторонние. Каково расстояние проползет улитка по пути ABCDFGHA?
Ответ: Расстояние пройденное улиткой будет равно 28 см.
Задача 44
В зале длиной 12 м и шириной 8 м надо покрыть пол квадратными плитками. Сколько потребуется плиток, если площадь каждой плитки 4 дм2?
Ответ: 2400 плиток.
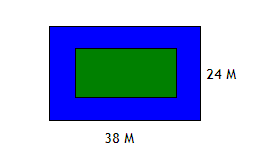
Задача 45
Каков периметр зеленой зоны, если ширина синей зоны равна 3 метра?
Ответ: Периметр зеленой зоны равен 100 метров.
Загрузить PDF
Загрузить PDF
Очень легко вычислить площадь правильного треугольника (это многоугольник!) и очень непросто сделать это в случае неправильного одиннадцатиугольника (это тоже многоугольник!). Данная статья расскажет вам, как вычислять площадь различных многоугольников.
-
1
Формула для нахождения площади правильного многоугольника: Площадь = 1/2 х периметр х апофема.
- Периметр – сумма сторон многоугольника.
- Апофема – отрезок, соединяющий центр многоугольника и середину любой из его сторон (апофема перпендикулярна стороне).
-
2
Найдите апофему. Она, как правило, дана в условии задачи. Например, дан шестиугольник, апофема которого равна 10√3.
-
3
Найдите периметр. Если периметр не дан в условии задачи, то его можно найти по известной апофеме.
- Шестиугольник можно разбить на 6 равносторонних треугольников. Апофема делит одну сторону пополам, создавая прямоугольный треугольник с углами 30-60-90 градусов.
- В прямоугольном треугольнике сторона, противолежащая углу в 60 градусов, равна x√3; углу в 30 градусов равна «х»; углу 90 градусов равна 2x. Если значение стороны x√3 равно 10√3, то х = 10.
- «х» – это половина длины основания треугольника. Удвойте ее и найдете полную длину основания. В нашем примере основание треугольника равно 20 единицам. В свою очередь основание треугольника есть сторона шестиугольника. Таким образом, периметр шестиугольника равен 20 х 6 = 120.
-
4
Подставьте значения апофемы и периметра в формулу. В нашем примере:
- площадь = 1/2 х 120 х 10√3
- площадь = 60 х 10√3
- площадь = 600√3
-
5
Упростите ответ. Возможно, вам придется записать ответ в виде десятичной дроби (то есть избавиться от корня). С помощью калькулятора найдите √3 и полученное число умножьте на 600: √3 х 600 = 1039,2. Это ваш окончательный ответ.
Реклама
-
1
Найдите площадь треугольника. Формула: Площадь = 1/2 х основание х высота.
- Если вам дан треугольник с основанием 10 и высотой 8, то его площадь = 1/2 х 8 х 10 = 40.
-
2
Найдите площадь квадрата. Чтобы найти площадь квадрата, просто возведите в квадрат длину одной его стороны. Если умножить основание квадрата на его высоту, мы получим тот же ответ, так как основание и высота равны.
- Если сторона квадрата равна 6, то его площадь = 6 х 6 = 36.
-
3
-
4
Найдите площадь трапеции. Формула: Площадь = [(основание1 + основание2) х высота] / 2.
- Например, дана трапеция с основаниями 6 и 8 и высотой 10. Ее площадь = [(6 + 8)•10]/2 = (14 х 10)/2 = 140/2 = 70.
Реклама
-
1
Используйте координаты вершин неправильного многоугольника. Зная координаты вершин, можно определить площадь неправильного многоугольника.
-
2
Сделайте таблицу. Запишите координаты вершин (х,у) (вершины выбирать последовательно в направлении против часовой стрелки). В конце списка еще раз напишите координату первой вершины.
-
3
Умножьте значение координаты «х» первой вершины на значение координаты «у» второй вершины (и так далее). Сложите результаты (в нашем примере сумма равна 82).
-
4
Умножьте значение координаты «у» первый вершины на значение координаты «х» второй вершины (и так далее). Сложите результаты (в нашем примере сумма равна -38).
-
5
Вычтите сумму, полученную в шаге 4, из суммы, полученной в шаге 3. В нашем примере: (82) — (-38) = 120.
-
6
Разделите полученный результат на 2, чтобы найти площадь многоугольника: S=120/2 = 60 (квадратных единиц).
Реклама
Советы
- Если вы записываете координаты вершин в направлении по часовой стрелке, вы получите отрицательную площадь. Таким образом, это можно использовать для описания цикла или последовательности данного набора вершин, формирующих многоугольник.
- Данная формула находит площадь с учетом формы многоугольника. Если многоугольник имеет форму цифры 8, то необходимо из площади с вершинами против часовой стрелки вычесть площадь с вершинами по часовой стрелке.
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 440 012 раз.