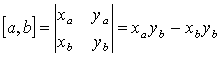Как найти площадь многоугольника по точкам - Исправление недочетов и поиск решений вместе с Examum.ru

Площадь по заданным координатам.

Как найти (вычислить) площадь фигуры (треугольник, четырехугольник, трапеция, многоугольник и др.) по координатам?

Какие есть формулы и методы, позволяющие находить площадь через координаты?

бонус за лучший ответ (выдан): 5 кредитов

Суть метода заключается в построении треугольников, состоящих из сторон многоугольника и лучей проведённых из начала координат к вершинам многоугольника, и сложении площадей треугольников, включающих внутреннюю часть многоугольника с вычитанием площадей треугольников, расположенных снаружи.

Площадь, вычисленная по приведенной формуле, будет иметь отрицательное значение при обходе фигуры по часовой стрелке и положительное при обходе против часовой стрелки.

Фигура многоугольника может иметь произвольную геометрию. Например:

Список координат многоугольника представлен в виде массива: (x1, y1), (x2, y2), (x3, y3),…(xn, yn).

Для многоугольника на первом рисунке он задан точками: (3,4), (5,11), (12,8), (9,5), (5,6). Его площадь будет равна:

Существует также метод трапеций, основанный на сложении и вычитании площадей трапеций, образованных каждой из сторон многоугольника, её проекцией на ось абсциссы и перпендикулярами, опущенных из вершин на абсциссу. При обходе вершин по часовой стрелке учитывается величина координаты вершин. Если первая вершина меньше второй, то площадь трапеции прибавляется, если нет, то отнимается.

Для многоугольника ABCDE на левом нижнем рисунке существует 5 трапеций : ABJH, CBJF, CDIF, EDIG и EAHG.

Так как X1<X2, X3<X4 и X5<X1, то площади трапеций ABJH, CDIF и EAHG складываются, а X3>X4 и X4<X5, следовательно, площади трапеций CBJF и EDIG вычитаются:

S = S(ABJH) – S(CBJF) + S(CDIF) – S(EDIG) + S(EAHG)

Площади трапеций рассчитываются по формуле;

Sтрапеции = 1/2 *((a+b))*h,

где a, b – основания трапеции,

h – высота трапеции.

Значения a, b и h вычисляются по координатам.

В декартовых координатах круг может быть представлен двумя точками: центр А и любая точка В, лежащая на окружности. Для расчета площади круга необходимо вычислить его радиус по формуле:

автор вопроса выбрал этот ответ лучшим

Ксарфакс
[156K]

5 лет назад

Площадь фигуры по координатам вершин

Если известны координаты всех вершин, то площадь заданной геометрической фигуры (треугольника, прямоугольника, трапеции, ромба и т.д) можно найти по стандартным формулам. Но предварительно нужно найти длину сторон, диагоналей и т.п. (всё зависит от фигуры) с помощью формулы нахождения длины отрезка по заданным координатам.

Эта формула выглядит следующим образом:

Здесь:

AB — отрезок,

точка A имеет координаты (x1, y1),

точка B имеет координаты (x2, y2).

Рассмотрим несколько примеров.

1) Треугольник ABC имеет координаты A(2,3); B(6,7); C(5,0). Его площадь можно найти по формуле Герона:

Здесь:

S — площадь треугольника,

a, b, c — стороны,

p — полупериметр, который равен половине суммы сторон a, b и c.

Найдём, чему равны стороны треугольника по формуле нахождения длины отрезка по координатам:

AB = √(4² + 4²) = √32 ≈ 5,66.

AC = √(3² + (-3)²) = √18 ≈ 4,24.

BC = √((-1)² + (-7)²) = √50 ≈ 7,07.

Полупериметр треугольника будет равен (5,66 + 4,24 + 7,07) / 2 ≈ 16,97 / 2 ≈ 8,49.

Отсюда площадь треугольника ABC ≈ √(8,49 * 2,83 * 4,25 * 1,42) ≈ √145 ≈ 12,04.

2) Ромб ABCD имеет координаты A(1,2); B(3,4); C(5,2); D(3,0). Площадь можно найти через диагонали:

Здесь:

S — площадь ромба,

d1 и d2 — диагонали.

Таким образом, нам нужно найти диагонали AC и BD.

AC = √(4² + 0) = √16 = 4.

BD = √(0 + (-4)²) = √16 = 4.

Отсюда площадь ромба ABCD = 0,5 * 4 * 4 = 8.

3) Трапеция ABCD имеет координаты A(1,1); B(3,4); C(5,4); D(6,1). Стандартная формула площади трапеции такая:

Здесь:

S — площадь трапеции,

a и b — основания,

h — высота.

Высота трапеции (пусть это будет BE) — это перпендикуляр, который был опущен из вершины трапеции (из точки B) на её основание (в нашем случае это AD).

Определим координаты её отрезка:

координаты первой точки совпадают с точкой B, это (3,4).
координаты 2 точки (точка E) будут (3,1) — так как абсцисса совпадает с абсциссой точки B, а ордината совпадает с ординатой точек A и D.

Высота трапеции BE = √(0 + (-3)²) = √9 = 3.

Теперь посчитаем длину оснований:

BC = √(2² + 0) = √4 = 2.

AD = √(5² + 0) = √25 = 5.

Таким образом, площадь трапеции ABCD = 3 * 0,5 * (2 + 5) = 10,5.

Степан-16
[34.5K]

6 лет назад

Первоначально нужно вычислить длины сторон. В этом здесь будет основная задача. Получив стороны, вычисляем площади по стандартным формулам.

Самый простой случай — для прямоугольника, когда его стороны параллельны осям координат. Тогда одна сторона будет равна разнице абсцисс, вторая ординат.

Треугольник. Допустим, основание параллельно оси абсцисс. Вычисляем его длину, как разницу абсцисс. Далее нужно найти высоту. Она будет равна разнице ординат третьей вершины и ординаты любой из вершин основания. Затем — площадь по формуле: половина произведения основания на высоту.

И т.д.

Если же стороны фигуры не параллельны осям, то находить длины сторон придется уже более сложными расчетами. Допустим, прямоугольник. Первую сторону будем искать, как если бы она была гипотенузой в составе прямоугольного треугольника. Каждая сторона будет равна квадратному корню из суммы квадратов абсцисс и ординат концов отрезков стороны.

Так и для любой фигуры. Вначале определяем длины сторон как гипотенузу треугольника. После чего применяем стандартные формулы площадей.

Эления
[445K]

3 года назад

Рассчитать площадь какой угодно геометрической фигуры, зная координаты, не составляет сложности. Каждая из точек, соответствующая вершинам искомой фигуры, будь это треугольник, четырех- или многоугольник, имеет определенную координату, а значит у нее есть значение, через которое можно рассчитать площадь.

Координаты, как найти на графике, чтобы узнать площадь фигуры? Проецируем на оси абсцисс и ординат прямые, проведя перпендикуляр из каждой точки. Полученные значения будут исходной величиной. Каждая из сторон фигуры — это разница двух точек на горизонтальную и вертикальную оси. Разница между значениями означает длину стороны фигуры. А зная все стороны и их значение, по формуле находим площадь.

Пример 1. Ищем площадь треугольника.

Мы видим два отрезка зеленого цвета AB и BC, которые образуют стороны равнобедренного треугольника, а основание есть отрезок на оси абсцисс AC.

Даны значения: AC основание в промежутке от «-4» до «+4», то есть длина основания равна восьми.

Будет лучше, если посчитать площадь этого треугольника, как сумму из образовавших его двух треугольников, которые являются прямыми, ABO и BOC, совпадающие прямым углом с координатой «0» на графике.

Известна длина каждй из сторон, образующих прямой угол (AO или OC) х = 4 — 0 = 4 и y = 2 — 0 = 2 (BO).

Зная длину двух сторон, образующих прямой угол (AO и BO), находим длину основания (AB или BC). Тогда уже знаем все длины каждой из сторон обоих прямых треугольников. Остается только найти площадь по формуле:

Зная площадь каждого из прямых треугольников, умножаем на два, получаем сумму заштрихованного треугольника на графике ABC.

И еще математически можно записать решение следующим образом, исходя из того, что имеем изначально следующую систему неравенств:

Пример 2.

Пример 3. Есть парабола, ищем площадь фигуры, ограниченную кривой параболы. Чтобы посчитать, используем интеграл.

Бекки Шарп
[71.2K]

3 года назад

Рассмотрим простой случай, где буквально на пальцах можно посчитать площадь через обычную формулу, а затем применим к этой задаче формулу Гаусса.

У нас есть трапеция, у которой известны координаты вершин. (3:2) (5:2) (9:6) (6:6). Мы знаем, что площадь трапеции равна сумме оснований, деленной на 2 и умноженной на высоту.

S = (a+b)/2 х h Считаем площадь: S = (3+2):2х4 = 10. Ответ — 10.

А теперь по теореме Гаусса.

Не смотря на страшный вид, формула очень простая. В квадратных скобках мы перемножаем абсциссу первой точки с ординатой второй, прибавляем абсциссу второй, умноженную на ординату третьей и так идем по кругу фигуры. Далее вычитаем ординату первой умноженную на абсциссу второй и т.д. В квадратных скобках у нас может получиться отрицательное число.

S= 0,5 х [3х6+6х6+9х2+5х2 — 2х6-6х9-6х5-2х3] = 10

Таким образом можно найти площадь любой сложной фигуры, зная ее координаты.

dydySacha
[10.8K]

6 лет назад

Можно взять милиметровку и нанести точки с заданными координатами, согласно осей абсцис и ординат. Соединить эти точки между собой и замерить длины образовавшихся сторон, а с помощью формулы по определению площади образовавшейся фигуры узнать её значение подставив данные в эту формулу.

Алиса в Стране
[364K]

3 года назад

Существует специальная формула, называемая формулой Гаусса, она и позволит нам определить искомую площадь по координатам. Вот как эта формула выглядит:

Формула выглядит немного устрашающе, но давайте попробуем в ней разобраться. У нас есть многоугольник и есть его координаты, подсчитать n — количество сторон многоугольника несложно, а дальше просто нужно подставлять значения в эту формулу, нужно только быть внимательным и не перепутать какие координаты куда надо писать.

Давайте теперь приведем пример нахождения такой площади через формулу Гаусса. Допустим, у нас есть вот такой пятиугольник:

Координаты его пяти вершин, как мы видим: (3, 4), (5, 11), (12, 8), (9, 5), (5, 6).

Теперь нам остается только очень внимательно подставить эти координаты в нашу формулу, n = 5, координаты известны, вот что у нас получится:

Когда разбираешься в этой формуле, понимаешь, насколько она проста и даже легко запоминается, несмотря на то, что сначала кажется очень сложной.

duselldorf
[4.3K]

5 лет назад

Для вычисления площади геометрической фигуры по координатам ее вершин, нужно воспользоваться формулой Гаусса, иногда ее называют формулой землемера или формулой геодезиста, так как она применяется геодезистами для определения площади земельного участка, например, при межевании:

где

А — площадь многоугольника с заданными координатам его вершин,

n — количество сторон многоугольника,

(xi, yi) — координаты вершин многоугольника,

i = 1, 2,…, n — номер вершины многоугольника.

Бархатные лапки
[382K]

3 года назад

Находим площадь вот такого несложного четырехугольника. Координаты его вершин нам известны. Применяем формулу Гаусса, которая выглядит так:

S (площадь) = 0,5 [6х4 +9х7 + 10х6 + 7х3 — 3х9 — 4х10 — 7х7 — 6х6] = 8 (квадратных единиц)

Как видим если применять при решении формулу Гаусса то решить такую задачку несложно.

Не вижу здесь серьезных проблем. Мы, как я понял, имеем готовые точки координат, которые нужно проставить на координатной плоскости. Далее, соединяя эти точки, получаем фигуру, как в примере вопроса — квадрат, треугольник и т.п.

Теперь вычисляем площадь любой из полученных фигур по формуле ей соответствующей.

Знаете ответ?

Источник

Калькулятор ниже был написан для решения частной задачи расчета площади выпуклого четырехугольника по координатам его вершин. Он только обобщает эту задачу до задачи расчета площади любого выпуклого многоугольника вообще. Собственно, на сайте уже был подобный калькулятор Площадь многоугольника, но там требовалось вводить длины сторон и диагоналей, а это несколько труднее, чем вводить только координаты вершин.

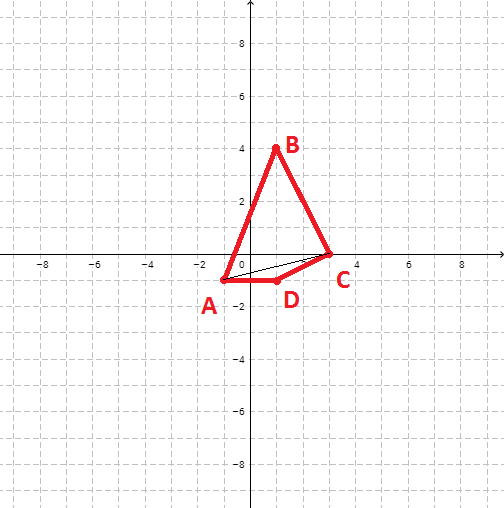
Принцип работы остается таким же — многоугольник разбивается на непересекающиеся треугольники, подсчитывается площадь всех треугольников (это легко сделать зная длины всех трех сторон — Расчет площади треугольника по формуле Герона), затем площади суммируются. Основная проблема была в том, чтобы сделать его устойчивым к ситуации, когда точки вводят не по порядку. Предположим, сначала вводят первые четыре точки получая фигуру на рисунке ниже

Четырехугольник

При добавлении следующей точки, например, так, как на следующем рисунке

Пятиугольник

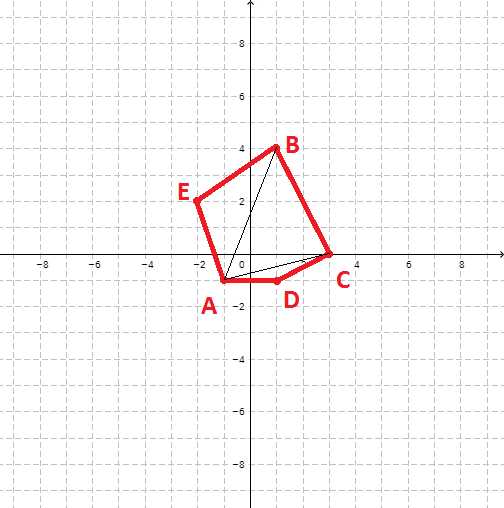
должен уже получиться многоугольник ADCBE, а не ABCDE, разбитый на треугольники ADC, ACB и ABE, соответственно.

Чтобы получить правильный многоугольник, фактически требуется получить оболочку введенных точек. Для этого калькулятор использует алгоритм Джарвиса (или алгоритм обхода Джарвиса, или алгоритм заворачивания подарка), который определяет последовательность элементов множества, образующих выпуклую оболочку для этого множества. Метод можно представить как обтягивание верёвкой множества вбитых в доску гвоздей.

Алгоритм работает за время O(nh) , где n — общее число точек на плоскости, h — число точек в выпуклой оболочке. Для выпуклого многоугольник соответственно будет O(n^2) . Не самый оптимальный алгоритм, зато очень простой, и для этого калькулятора вполне производительный.

Как пользоваться калькулятором: начинаете вводить координаты точек выпуклого многоугольника. Начиная с трех точек алгоритм Джарвиса будет стоить обтягивающий контур, затем контур будет разбиваться треугольники и подсчитываться общая площадь. Для справки также будут выводиться площади всех треугольников.

Вычисление площади выпуклого многоугольника по координатам вершин на плоскости

Точки многоугольника

	Точка	X	Y

Точность вычисления

Знаков после запятой: 2

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Источник

Данный сайт находится в режиме тестирования, обо всех выявленных проблемах Вы можете сообщить на почту

Векторная алгебра

Площадь фигуры по координатам
Длина линии по координатам
Координаты точки пересечения линий
Площадь фигуры по координатам
Расстояние между точкой и прямой
Действия с векторами

Количество знаков дробной части

Координаты точки 1

Координаты точки 2

Координаты точки 3

Примечание: Вводить точки необходимо с крайней левой, относительно центра координат по часовой стрелке.
Если фигура с пересекающимися линиями, то последовательно по точкам «движения» линии.

Источник

Для вычисления площади простого многоугольника с любым количеством вершин, представленных в виде списка координат, при последовательном обходе которых, не образуются пересекающиеся линии, применяется формула Гаусса, иначе называемая «формулой землемера», «формулой геодезиста», «формулой шнурования», «алгоритмом шнурования», а также «методом треугольников».
Суть метода заключается в построении треугольников, состоящих из сторон многоугольника и лучей проведённых из начала координат к вершинам многоугольника, и сложении площадей треугольников, включающих внутреннюю часть многоугольника с вычитанием площадей треугольников, расположенных снаружи.

Формула Гаусса

S — площадь многоугольника,
n — количество сторон многоугольника,
(x_i, y_i), i = 1, 2, …, n — координаты вершин многоугольника.

Примеры

1. Для применения формулы необходимо знать координаты вершин многоугольника в декартовой плоскости. Для примера возьмём треугольник с координатами {(2, 1), (4, 5), (7, 8)}. Возьмём первую координату x первой вершины и умножим её на координату y второй вершины, а затем умножим х второй вершины на y третьей. Повторим эту процедуру для всех вершин. Результат может быть определён по следующей формуле:

где x_i и y_i обозначают соответствующую координату. Эту формулу можно получить, раскрыв скобки в общей формуле для случая n = 3. По этой формуле можно обнаружить, что площадь треугольника равна половине суммы 10 + 32 + 7 − 4 − 35 − 16, что даёт 3.

Число переменных в формуле зависит от числа сторон многоугольника. Например, в формуле для площади пятиугольника будут использоваться переменные до x₅ и y₅:

S для четырехугольника — переменные до x₄ и y₄:

2. Рассмотрим многоугольник, представленный на рисунке и заданный точками (3, 4), (5, 11), (12, 8), (9, 5), (5, 6):

Площадь этого многоугольника:

Подпрограмма «Площадь и объем» на электронном тахеометре Leica серии TS02/06/09

Подпрограмма позволяет вычислять площади участков, ограниченных максимум 50-ю точками, соединенных отрезками прямой. Эти точки должны быть измерены, взяты из памяти либо заданы с клавиатуры — с расположением их по часовой стрелке. Вычисленная площадь проектируется на горизонтальную плоскость (2D) или на наклонную опорную плоскость, заданную своими тремя точками (3D). Кроме того, можно вычислить объем, заключенный между плоскостью с постоянной высотной отметкой и заданным полигоном (2D/3D).

P0 — Точка установки инструмента
P1 — Начальная точка
P2 — Проектная точка
P3 — Точка визирования
P4 — Точка визирования
a — Суммарная длина всех сегментов границы полигона от начальной точки до текущей измеренной точки.
b — Вычисленная площадь полигона, замыкающегося на начальную точку P1 и спроектированная на горизонтальную плоскость.

Вызов подпрограммы

1. Выберите Программы в Главном меню.
2. Откройте окно Площадь и объем из меню Программы.

На дисплее всегда будет показываться площадь, спроектированная на горизонтальную плоскость.

Назад — Отбраковка измерений или отмена выбора предыдущей точки.
РЕЗ-ТЫ — Вывод на дисплей и запись дополнительных результатов (периметр, объем).
ОБЪЕМ — Вычисление объема до плоскости с постоянной высотной отметкой. Отметка должна быть введена с клавиатуры или измерена.
Опр. 3D — Здесь можно задать наклонную опорную плоскость, выбрав в памяти или измерив три ее точки.
2D-площади будут вычисляться и выводиться на дисплей, как только три точки будут взяты из памяти или измерены. 3D-площади вычисляются после определения наклонной отсчетной плоскости по трем точкам.

Графическая визуализация

P0 — Точка установки инструмента
P1 — Точка для задания наклонной отсчетной плоскости
P2 — Точка для задания наклонной отсчетной плоскости
P3 — Точка для задания наклонной отсчетной плоскости
P4 — Точка визирования
a — Постоянная высотная отметка
b — Периметр (3D), т.е. общая длина сегментов границы полигона от начальной до текущей точки c Площадь (3D), спроектированная на наклонную отсчетную плоскость
d — Объем (3D) = a х c e Периметр (2D), т.е. общая длина сегментов границы полигона от начальной до текущей точки площади 2D
f — Площадь (2D), спроектированная на горизонтальную плоскость
g — Объем (2D) = f x a
Следующий шаг Нажмите на Рез-т для вычисления площади и объема и перехода в окно Площадь и Объем — Рез-ты.

Результаты измерений

Значения периметра и объема постоянно обновляются по мере добавления новых точек.
Следующий шаг
• Нажмите на Нов.у-д для определения нового участка,
• либо на Дп.т-ка для добавления новой точки границы текущего полигона.
• либо на ESC для выхода из программы.

Источник

Просмотров 10.5к. Обновлено 23 ноября 2020

Урок из серии «Геометрические алгоритмы»

Здравствуйте, дорогой читатель.

Решения многих задач вычислительной геометрии основывается на нахождении площади многоугольника. На этом уроке мы выведем формулу для вычисления площади многоугольника через координаты его вершин, напишем функцию для вычисления этой площади.

Задача. Вычислить площадь многоугольника, заданного координатами своих вершин, в порядке их обхода по часовой стрелке.

Сведения из вычислительной геометрии

Для вывода формулы площади многоугольника нам понадобятся сведения из вычислительной геометрии, а именно, понятие ориентированной площади треугольника.

Ориентированная площадь треугольника – это обычная площадь, снабженная знаком. Знак ориентированной площади треугольника АВС такой же, как у ориентированного угла между векторами и . То есть ее знак зависит от порядка перечисления вершин.

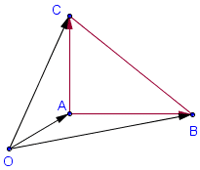
Рис1

На рис. 1 треугольник АВС – прямоугольный. Его ориентированная площадь равна 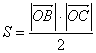(она больше нуля, так как пара , ориентирована положительно). Эту же величину можно вычислить другим способом.

Пусть О – произвольная точка плоскости. На нашем рисунке площадь треугольника ABC получится, если из площади треугольника OBC вычесть площади OAB и OCA. Таким образом, нужно просто сложить ориентированные площади треугольников OAB, OBC и OCA. Это правило работает при любом выборе точки О.

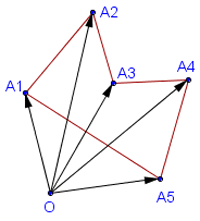
Точно так же для вычисления площади любого многоугольника нужно сложить ориентированные площади треугольников

Рис. 2

В сумме получится площадь многоугольника, взятая со знаком плюс, если при обходе ломаной многоугольника находится слева (обход границы против часовой стрелки), и со знаком минус, если он находится справа (обход по часовой стрелке).

Итак, вычисление площади многоугольника свелось к нахождению площади треугольника. Посмотрим, как выразить ее в координатах.

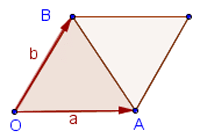
Векторное произведение двух векторов на плоскости есть площадь параллелограмма, построенного на этих векторах.

Векторное произведение, выраженное через координаты векторов:

Площадь треугольника будет равна половине этой площади:

В качестве точки О удобно взять начало координат, тогда координаты векторов, на основании которых вычисляются ориентированные площади, совпадут с координатами точек.

Пусть (х₁, y₁), (x₂, у₂), …, (х_N,у_N) —координаты вершин заданного многоугольника в порядке обхода по или против часовой стрелки. Тогда его ориентированная площадь S будет равна:

Это и есть наша рабочая формула, она используется в нашей программе.

Если координаты вершин были заданы в порядке обхода против часовой стрелки, то число S,вычисленное по этой формуле, получится положительным. В противном случае оно будет отрицательным, и для получения обычной геометрической площади нам необходимо взять его абсолютное значение.

Итак, рассмотрим программу для нахождения площади многоугольника, заданного координатами вершин.

Program geom6;
Const n_max=200; {максимальное количество точек+1}

type b=record
         x,y:real;
       end;
     myArray= array[1..n_max] of b;
var input:text;
    A:myArray;
    s:real;
    i,n:integer;

procedure ZapMas(var n:integer; var A:myArray);
{Заполнение массива }
begin
  assign(input,'input.pas');
  reset(input);
  readln(input, n);
  for i:=1 to n do
    read(input, a[i].x,a[i].y);
  close(input);
end;

function Square (A:myarray): real;
{Вычисление площади многоугольника}
var i:integer;
     S: real;
begin
   a[n+1].x:=a[1].x;    a[n+1].y:=a[1].y;
   s:=0;
   for i:=1 to n do
      s := s + (a[i].x*a[i+1].y - a[i].y*a[i+1].x);
   s:=abs(s/2);
   Square := S
end;  {Square}
begin {main}
   Zapmas(n, a);
   PrintMas(a);
   S:= Square(a);
   writeln('S= ',s:6:2);

end.

Координаты вершин считывается из файла input.pas., хранятся в массиве А в виде записей с двумя полями. Для удобства обхода многоугольника в массиве вводится n+1 элемент, значение которого равно значению первого элемента массива.

Входные данные:
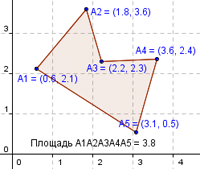
5
0.6 2.1 1.8 3.6 2.2 2.3 3.6 2.4 3.1 0.5

Выходные данные:
S= 3.91

Мы решили задачу о нахождении площади многоугольника по координатам его вершин. Задачи усложняются. Если у вас есть замечания к этой статье, или пожелания, напишите в комментарии. Буду Вам очень признательна за сотрудничество.

До встречи на следующем уроке.

Источник