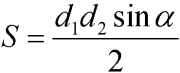Как найти площадь неравнобедренного прямоугольника - Исправление недочетов и поиск решений вместе с Examum.ru

С помощью данного калькулятора вы можете легко и быстро рассчитать площадь неправильного четырехугольника в условных единицах. Инструмент позволяет определить площадь выпуклой фигуры тремя разными способами: по сторонам, сторонам и углам, диагоналям и углам (первые два вычисления выполняются с ограничениями). Теоретическое обоснование расчета и формулы представлены ниже. Чтобы получить результат — выберите наиболее подходящий метод расчета, заполните поля калькулятора и нажмите кнопку «Рассчитать».

Как найти площадь неправильного четырехугольника?

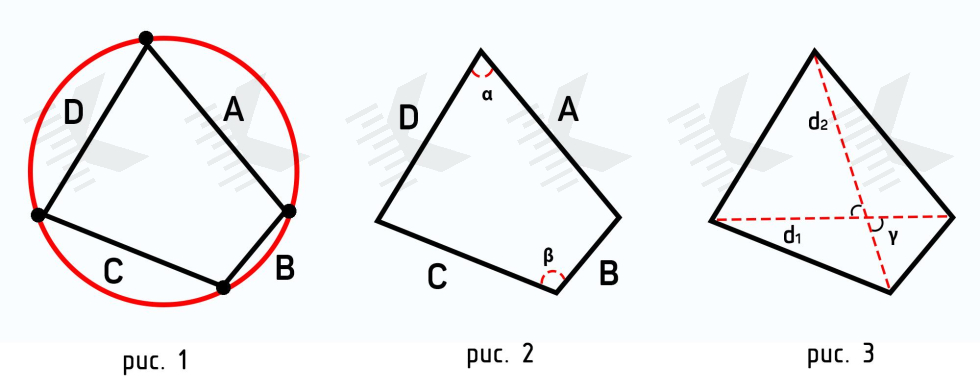
Первый способ расчета основан на формуле Брахмагупты (рис. 1), которая выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон. Эта формула является обобщением формулы Герона для площади треугольника.

где P — полупериметр, a, b, c, d — длины сторон четырехугольника.

Вторая формула также основывается на формуле Брахмагупты, но на ее расширенной версии (рис. 2), когда необходимо найти площадь произвольного четырехугольника.

где P — полупериметр, a, b, c, d — длины сторон, θ — полусумма противоположных углов четырёхугольника.

В формулах Брахмагупты есть одно ограничение — любая из сторон не может превышать полупериметр. В противном случае стороны четырехугольника не замкнутся. Математически, в формуле появится отрицательное значение.

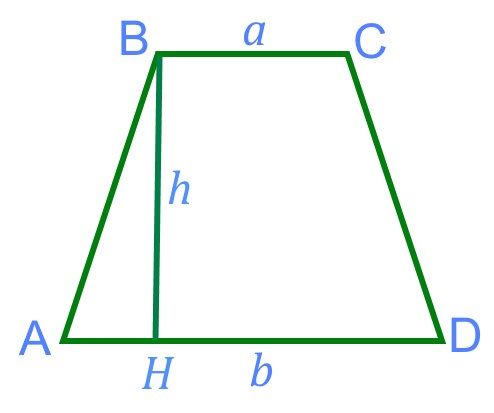
Последняя формула позволяет найти площадь не самопересекающейся фигуры по проведенным диагоналям и синусу угла между ними (рис. 3). По сути, формула основывается на сумме площадей треугольников, которые образуются диагоналями четырехугольника.

где d₁, d₂ — диагонали четырехугольника, α — острый угол между диагоналями.

Источник

С завидным упорством некоторые пользователи Planetcalc оставляют запросы на создание калькулятора для расчета площади неправильного четырехугольника, для которого известны только длины сторон. Подумалось, что остановить их можно только написав вот такой шуточный калькулятор. (Нажмите кнопку «Остановить» для определения площади понравившегося Вам четырехугольника с заданными Вами сторонами).

Площадь четырехугольника

Точность вычисления

Знаков после запятой: 2

Четырехугольник

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Площадь неправильного четырехугольника, зная только длины сторон, вычислить нельзя. Надеюсь, эта демонстрация поможет понять это всем, кто просил создать для этого калькулятор.

Источник

На чтение 9 мин. Просмотров 4.5k.

Формулы для вычисления площади всех видов трапеции, онлайн калькуляторы для расчета. Вывод основной формулы и примеры применения формул в задачах. Удобный справочный материал с подробными объяснениями.

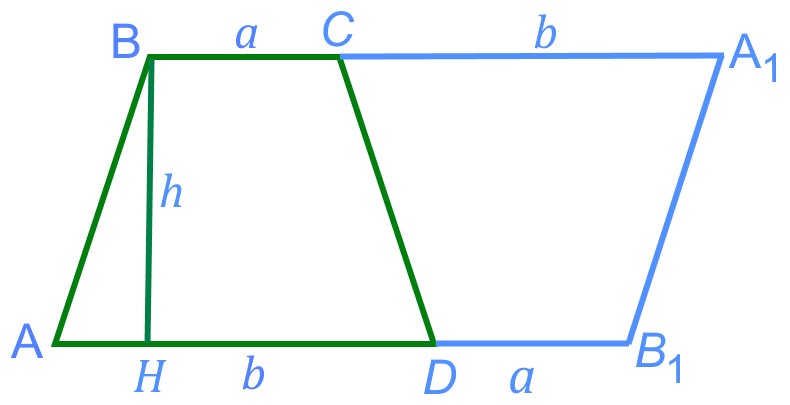
Чему равна площадь трапеции? Трапеция это важная и часто исследуемая геометрическая фигура в курсе геометрии, начиная с 7 класса. В процессе обучения школьники учатся решать задачи по геометрии на нахождение боковых сторон и оснований трапеции, углов и средней линии. Важно уметь находить периметр и площадь трапеции. Рассмотрим чему равна площадь трапеции и решим несколько задач на нахождение площади трапеции.

Как найти площадь произвольной трапеции
- Доказательство 1
- Доказательство 2
Примеры решения задач
- Задача 1
- Задача 2
Формулы площади трапеции для всех трапеций
По высоте и основаниям
- По высоте и средней линии
- По известным четырем сторонам
- По известным основаниям и углам при основании
- По двум диагоналям и углу между ними
- Площадь прямоугольной трапеции
- Площадь равнобедренной трапеции
Таблица формул для определения площади трапеции

Как найти площадь произвольной трапеции

Площадь трапеции $S_{ABCD}$ равна произведению полусуммы её оснований на высоту трапеции.

$S_{ABCD}=frac{1}{2} cdot (BC+AD) cdot BH$

Трапеция ABCD

Единицей измерения площади является квадратная единица длины: м², см², кв.ед., км².

Докажем, что данная формула верна для любой трапеции.

Доказательство 1

Пусть нам дана трапеция , проведем из вершины высоту трапеции на сторону .

Продлим сторону на длину основания получим точку . Продлим сторону трапеции на длину стороны . Получим точку .

Соединим точки и . Трапеция равна трапеции по построению.

Полученный в результате построения четырехугольник — параллелограмм, площадь которого равна двум площадям трапеции :

$S_{ABA_1B_1}=AB_1 cdot BH$

Отсюда площадь трапеции

$S_{ABCD}=frac{1}{2} cdot AB_1 cdot BHAB_1 cdot BH=frac{1}{2} cdot (AD+DB_1) cdot BH$

так как , то получим:

$S_{ABCD}=frac{1}{2} cdot (AD+BC) cdot BH$ .

Таким образом, $S=frac{1}{2 }(a+b)h$ .

Что и требовалось доказать.

Доказательство 2

Достроим трапецию ABCD до прямоугольника, получим прямоугольник .

Площадь трапеции можно получить, если вычесть из площади прямоугольника площади достроенных треугольников.

Построение прямоугольника из трапеции для доказательства

Находим $S_{ABCD}=hb-(S_1+S_2)=hb-frac{1}{2}(hm+hn)=hb-frac{1}{2}h(m+n)=hb-frac{1}{2}h(b-a)=hb-frac{1}{2}hb+frac{1}{2}ha=frac{1}{2}h(b+a)$ .

Можно еще привести множество доказательств правильности формулы для площади трапеции, но двух уже достаточно.

Давайте теперь решим несколько задач на нахождение площади трапеции.

Как найти площадь равнобедренной трапеции? Точно также как и площадь любой другой трапеции. Формула одна и та же.

Примеры решения задач

Решим задачи, в которых нужно узнать площадь трапеции.

Задача 1

Вычислить площадь четырехугольника $S_{ABCD}$ , если известно, что , и боковая сторона перпендикулярна к , а .

Решение.

По последнему условию боковая сторона является высотой трапеции.

Рисунок к задаче 1

Тогда $S_{ABCD}=frac{1}{2} cdot 5 cdot (5+7)=30$ .

Ответ: 30.

Задача 2

Дана трапеция . Известно, что см, , см, а ∠=30°. Найти $S_{ABCD}$ .

Рисунок к задаче 2 площадь трапеции

Решение:

Для определения площади нам потребуется знать высоту . Определим ее из прямоугольного треугольника . Катет, лежащий напротив угла в 30 градусов равен половине гипотенузы, а, следовательно, см.

Определим . Так как , то получим: см.

Тогда $S_{ABCD}=frac{1}{2} cdot h (AD+BC)=frac{1}{2} cdot 1,5 (8+4)=9$ см.

Ответ: 9 см.

Формулы площади трапеции для всех трапеций

Ниже приведем все формулы для определения площади трапеции, которые можно использовать. Однако, многие из них выводятся из основной, приведенной выше и редко используются как самостоятельные. Запоминать их нет необходимости, так как их всегда можно вывести. Однако, если вам дана задача с исходными данными и нужно проверить правильность ее решения, именно с исходными данными (например, даны только длины всех сторон трапеции, а нужно найти ее площадь), то используйте наши онлайн-калькуляторы.

По высоте и основаниям

Проверьте вычисления, используя наш онлайн калькулятор. Десятичные дроби вводите через точку. Ориентируйтесь на обозначения на рисунке.

Введите длину нижнего основания трапеции (на рисунке ) :

Введите длину верхнего основания трапеции (на рисунке ) :

Введите значение высоты трапеции h :

Площадь трапеции $S_{ABCD}=frac{1}{2}h(AD+BC)=$

По высоте и средней линии

Если дана высота и средняя линяя трапеции, то ее площадь можно найти по формуле:

где — средняя линия трапеции,

— высота.

Введите высоту трапеции :

Введите длину средней линии :

Площадь трапеции $S_{ABCD}=hm=$

По известным четырем сторонам

Если известны стороны трапеции , , , , то формула площади:

$S=displaystyle frac{a+b}{2}sqrt{c^2-left(frac{(b-a)^2+c^2-d^2}{2(b-a)}right)^2}$

Вы можете воспользоваться онлайн калькулятором:

Введите сторону :

Площадь трапеции 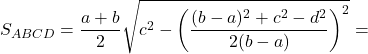$S_{ABCD}=displaystyle frac{a+b}{2}sqrt{c^2-left(frac{(b-a)^2+c^2-d^2}{2(b-a)}right)^2}=$

По известным основаниям и углам при основании

Если известны стороны трапеции , и углы при основании, то формула площади:

$S=displaystyle frac{b^2-a^2}{2}cdot frac{sin{alpha} cdot sin{beta}}{sin{(alpha+beta)}}$

Вы можете воспользоваться онлайн калькулятором:

Введите сторону :

Введите угол (в градусах) :

Введите угол (в градусах ):

Площадь трапеции $S=displaystyle frac{b^2-a^2}{2}cdot frac{sin{alpha} cdot sin{beta}}{sin{(alpha+beta)}}=$

По двум диагоналям и углу между ними

Если известны диагонали трапеции , и угол между ними, то формула площади трапеции:

$S=displaystyle frac{1}{2}cdot d_1 cdot d_2 cdot sin{alpha}$

Если вам известны эти величины, то можно быстро найти площадь, используя наш калькулятор онлайн:

Введите диагональ :

Введите угол (в градусах) :

Площадь трапеции $S=displaystyle displaystyle frac{1}{2}cdot d_1 cdot d_2 cdot sin{alpha}=$

Площадь прямоугольной трапеции

Если известны основания прямоугольной трапеции , и угол у большего основания, то формула площади трапеции:

$S=displaystyle frac{b^2-a^2}{2} tg alpha$

Вывод формулы: действительно, для произвольной неравнобедренной и не прямоугольной трапеции площадь по известным основаниям и углам при основании определяется по формуле:

$S=displaystyle frac{b^2-a^2}{2}cdot frac{sin{alpha} cdot sin{beta}}{sin{(alpha+beta)}}$ .

Если угол при основании равен 90 градусов (для прямоугольной трапеции) (пусть это угол ) то получим

$S=displaystyle frac{b^2-a^2}{2}cdot frac{sin{alpha}}{sin{(alpha+frac{pi}{2})}}$ .

По формулам приведения $sin{(alpha}+frac{pi}{2})}=cos{alpha}$

Тогда формула примет вид:

$S=displaystyle frac{b^2-a^2}{2}cdot frac{sin{alpha}}{cos{alpha}}$ , так как $displaystyle frac{sin alpha}{cos{alpha}}=tg alpha$ , то окончательно получается:

$S=displaystyle frac{b^2-a^2}{2}cdot tg alpha$

Если вам известны эти величины, то можно быстро найти площадь, используя наш калькулятор онлайн:

Сторона :

Введите угол (в градусах) :

Площадь трапеции $S=displaystyle frac{b^2-a^2}{2} tg alpha=$

Площадь равнобедренной трапеции

Площадь равнобедренной трапеции можно найти по любой из вышеприведенных формул, кроме формулы для прямоугольной трапеции, если ввести одинаковые значения для боковых сторон.

Например, формула нахождения площади по известным сторонам, упростится и будет иметь вид:

$displaystyle S=frac{1}{2}(a+b) cdot sqrt{c^2-left( frac{a-b}{2}right)^2}$

Сторона :

Площадь трапеции 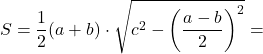$displaystyle S=frac{1}{2}(a+b) cdot sqrt{c^2-left( frac{a-b}{2}right)^2}=$

Таблица формул для определения площади трапеции

Сведем для удобства все формулы в таблицу. Если вам дана прямоугольная или равнобедренная трапеция, вы всегда можете определить ее площадь по любой из формул для неравнобедренной (произвольной) трапеции, просто введите одинаковые значения для боковой стороны.

Известные величины для расчета	Рисунок	Формула
Высота и основания		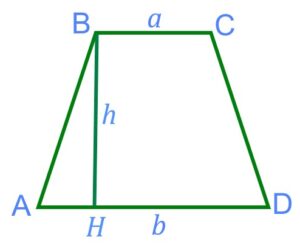$S_{ABCD}=frac{1}{2}h(AD+BC)$
Высота и средняя линия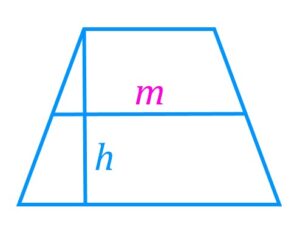
Все стороны		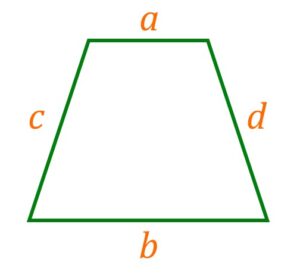$S=displaystyle frac{a+b}{2}sqrt{c^2-left(frac{(b-a)^2+c^2-d^2}{2(b-a)}right)^2}$
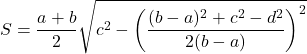Основания и углы при основании		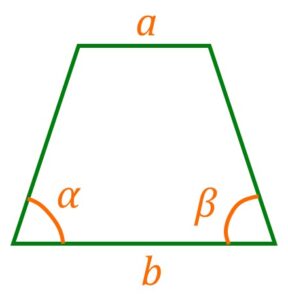$S=displaystyle frac{b^2-a^2}{2}cdot frac{sin{alpha} cdot sin{beta}}{sin{(alpha+beta)}}$
Две диагонали и угол между ними		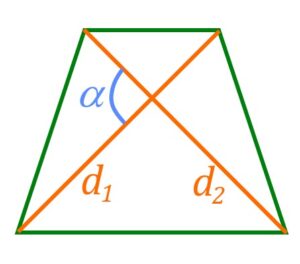$S=displaystyle frac{1}{2}cdot d_1 cdot d_2 cdot sin{alpha}$
Угол при основании 90° (случай прямоугольной трапеции), известен другой угол при основании и основания		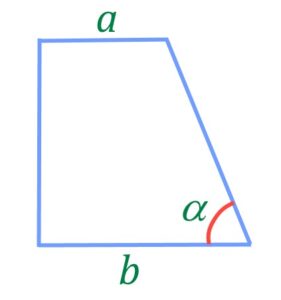$S=displaystyle frac{b^2-a^2}{2} tg alpha$
Боковые стороны равны (случай равнобедренной трапеции), известны стороны		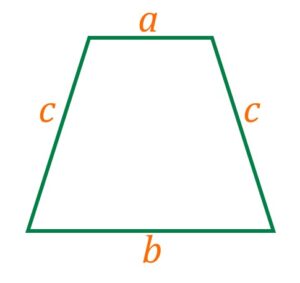$displaystyle S=frac{1}{2}(a+b) cdot sqrt{c^2-left( frac{a-b}{2}right)^2}$

Источник

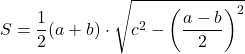В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.

Расчет площади
- 1. Через диагонали и угол между ними
- 2. По всем сторонам (формула Брахмагупты)
- 3. Через полупериметр и радиус вписанной окружности

Расчет площади

Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.

1. Через диагонали и угол между ними

Формула расчета

2. По всем сторонам (формула Брахмагупты)

Примечание: Если вокруг четырехугольника можно описать окружность.

Формула расчета

p – полупериметр четырехугольника, равняется:

3. Через полупериметр и радиус вписанной окружности

Формула расчета

S = p ⋅ r

Источник

Укажите размеры:

Основание

Высота

Результат:

Решение:

Ссылка на страницу с результатом:

# Теория

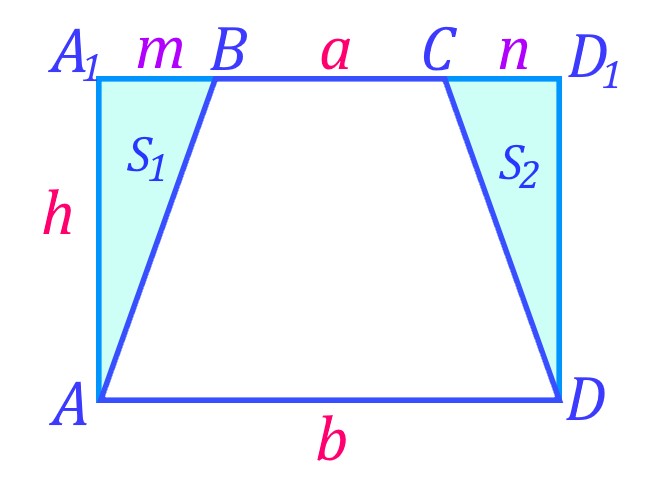
Трапеция — это четырёхугольник у которого две противоположные стороны параллельны и не равны между собой. Параллельные стороны трапеции называются основаниями, а две другие стороны называются боковыми.

Бывают прямоугольная, равнобедренная и неравнобедренная трапеции.

Неравнобедренная трапеция — это трапеция у которой боковые стороны не равны.

Основания трапеции — это две параллельные противоположные стороны.

Высота трапеции — это отрезок соединяющий основания под прямым углом.

Формула площади трапеции

Чтобы посчитать площадь трапеции, необходимо знать её основания и высоту.

Площадь трапеции расчитывается по формуле:

a
b
h

S =dfrac{1}{2} (a + b) cdot h

S — площадь трапеции;
a — основание трапиции;
b — основание трапеции
h — высота трапеции

Как найти площадь неправильного четырехугольника?

Площадь четырехугольника

Как найти площадь произвольной трапеции

Доказательство 1

Доказательство 2

Примеры решения задач

Задача 1

Задача 2

Формулы площади трапеции для всех трапеций

По высоте и основаниям

По высоте и средней линии

По известным четырем сторонам

По известным основаниям и углам при основании

По двум диагоналям и углу между ними

Площадь прямоугольной трапеции

Площадь равнобедренной трапеции

Таблица формул для определения площади трапеции

Расчет площади

1. Через диагонали и угол между ними

2. По всем сторонам (формула Брахмагупты)

3. Через полупериметр и радиус вписанной окружности

Формула площади трапеции

Похожие калькуляторы: