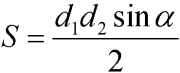Как найти площадь невыпуклого четырехугольника - Исправление недочетов и поиск решений вместе с Examum.ru

Площади четырехугольников

В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:

которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.

Формулы для площадей четырехугольников

a и b – смежные стороны

d – диагональ,
φ – любой из четырёх углов между диагоналями

Получается из верхней формулы подстановкой d=2R

R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

a – сторона,
h_a – высота, опущенная на эту сторону

a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

a – сторона квадрата

Получается из верхней формулы подстановкой d = 2R

a – сторона,
h_a – высота, опущенная на эту сторону

a – сторона,
φ – любой из четырёх углов ромба

r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

a и b – основания,
h – высота

φ – любой из четырёх углов между ними

a и b – основания,
c и d – боковые стороны

a и b – неравные стороны,
φ – угол между ними

a и b – неравные стороны,
φ₁ – угол между сторонами, равными a ,
φ₂ – угол между сторонами, равными b .

a и b – неравные стороны,
r – радиус вписанной окружности

φ – любой из четырёх углов между ними

a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,

Формулу называют «Формула Брахмагупты»

Четырехугольник	Рисунок	Формула площади	Обозначения
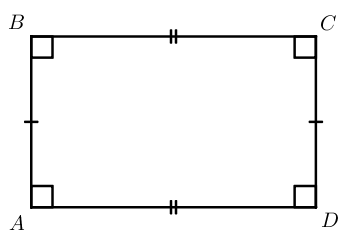
Прямоугольник		S = ab


Параллелограмм


Квадрат		S = a 2
	S = 4r 2


Ромб




Трапеция
	S = m h


Дельтоид		S = ab sin φ



Произвольный выпуклый четырёхугольник
Вписанный четырёхугольник

где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

Формула получается из верхней формулы подстановкой d = 2R

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Получается из верхней формулы подстановкой d = 2R

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба

где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

где
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
r – радиус вписанной окружности

φ – любой из четырёх углов между ними

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр

Формулу называют «Формула Брахмагупты»

Прямоугольник



Параллелограмм



Квадрат
	S = a 2 где a – сторона квадрата
	S = 4r 2


Ромб





Трапеция




Дельтоид

	где a и b – неравные стороны, φ₁ – угол между сторонами, равными a , φ₂ – угол между сторонами, равными b .


Произвольный выпуклый четырёхугольник

Вписанный четырёхугольник

Прямоугольник

где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

Формула получается из верхней формулы подстановкой d = 2R

Параллелограмм

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Квадрат

где
a – сторона квадрата

Получается из верхней формулы подстановкой d = 2R

Ромб

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба

где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

Трапеция

где
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны ,

Дельтоид

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
φ₁ – угол между сторонами, равными a ,
φ₂ – угол между сторонами, равными b .

где
a и b – неравные стороны,
r – радиус вписанной окружности

Произвольный выпуклый четырёхугольник

φ – любой из четырёх углов между ними

Вписанный четырёхугольник

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр

Формулу называют «Формула Брахмагупты»

Вывод формул для площадей четырехугольников

Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле

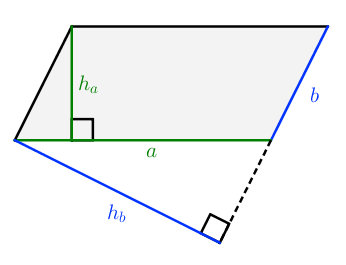
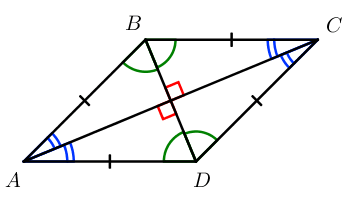
Доказательство . В соответствии с рисунком 1 справедливо равенство:

что и требовалось доказать.

Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле

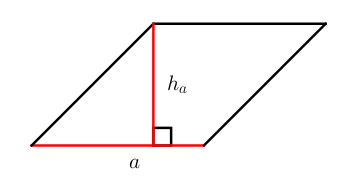
где a – сторона параллелограмма, а h_a – высота высота высота , опущенная на эту сторону (рис. 2).

Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому

что и требовалось доказать.

Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле

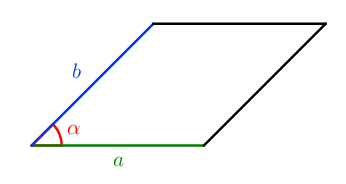
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).

то, в силу утверждения 2, справедлива формула

что и требовалось доказать.

Утверждение 4 . Площадь ромба ромба можно найти по формуле

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).

что и требовалось доказать.

Утверждение 5 . Площадь трапеции можно найти по формуле

где a и b – основания трапеции, а h – высота высота высота (рис.5).

Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому

что и требовалось доказать.

Утверждение 6 . Площадь трапеции трапеции можно найти по формуле

где a и b – основания, а c и d – боковые стороны трапеции ,

(рис.6).

Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

что и требовалось доказать.

Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:

где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).

Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.

Если r – радиус вписанной в дельтоид окружности, то

Площадь неправильного четырехугольника

Узнайте чему равна площадь неправильного четырехугольника с помощью онлайн-калькулятора или по формулам — расчет по сторонам, диагоналям, углам.

С помощью данного калькулятора вы можете легко и быстро рассчитать площадь неправильного четырехугольника в условных единицах. Инструмент позволяет определить площадь выпуклой фигуры тремя разными способами: по сторонам, сторонам и углам, диагоналям и углам (первые два вычисления выполняются с ограничениями). Теоретическое обоснование расчета и формулы представлены ниже. Чтобы получить результат — выберите наиболее подходящий метод расчета, заполните поля калькулятора и нажмите кнопку «Рассчитать».

Как найти площадь неправильного четырехугольника?

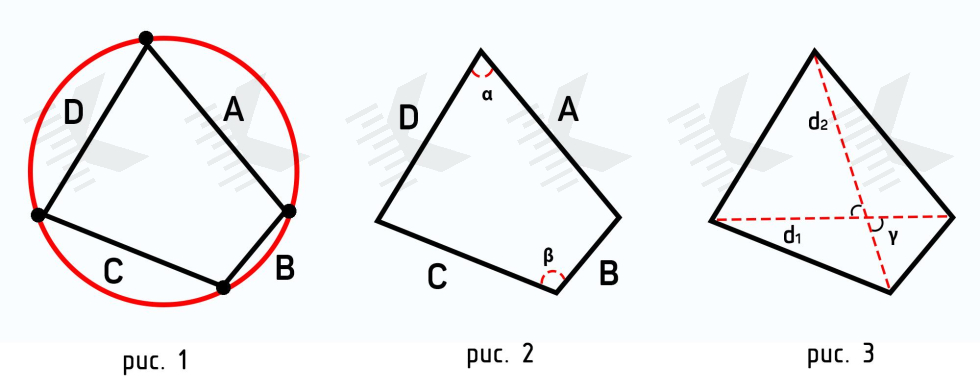
Первый способ расчета основан на формуле Брахмагупты (рис. 1), которая выражает площадь вписанного в окружность четырёхугольника как функцию длин его сторон. Эта формула является обобщением формулы Герона для площади треугольника.

где P — полупериметр, a, b, c, d — длины сторон четырехугольника.

Вторая формула также основывается на формуле Брахмагупты, но на ее расширенной версии (рис. 2), когда необходимо найти площадь произвольного четырехугольника.

где P — полупериметр, a, b, c, d — длины сторон, θ — полусумма противоположных углов четырёхугольника.

В формулах Брахмагупты есть одно ограничение — любая из сторон не может превышать полупериметр. В противном случае стороны четырехугольника не замкнутся. Математически, в формуле появится отрицательное значение.

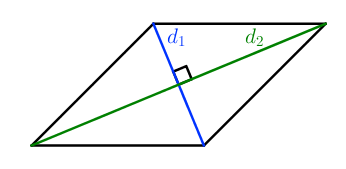
Последняя формула позволяет найти площадь не самопересекающейся фигуры по проведенным диагоналям и синусу угла между ними (рис. 3). По сути, формула основывается на сумме площадей треугольников, которые образуются диагоналями четырехугольника.

где d₁, d₂ — диагонали четырехугольника, α — острый угол между диагоналями .

Калькулятор расчета площади четырехугольника

В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.

Расчет площади

Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.

1. Через диагонали и угол между ними

Формула расчета

2. По всем сторонам (формула Брахмагупты)

Примечание: Если вокруг четырехугольника можно описать окружность.

Формула расчета

p – полупериметр четырехугольника, равняется:

источники:

http://kalk.pro/math/area/ploshad-nepravilnogo-chetyrehugolnika/

Калькулятор расчета площади четырехугольника

Источник

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

Определение четырехугольника

Четырехугольником называется фигура, которая состоит из четырех точек (вершин) и четырех отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.

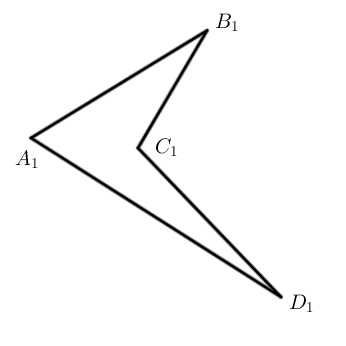
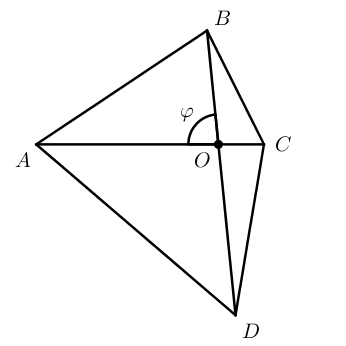
Четырехугольники бывают выпуклые ( A B C D ) и невыпуклые ( A 1 B 1 C 1 D 1 ) .

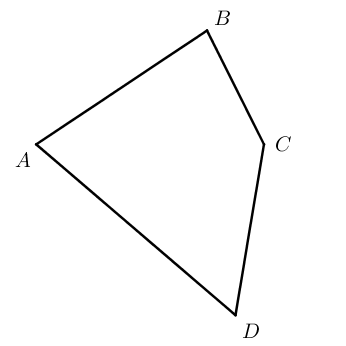
Выпуклые четырехугольники

В задачах ОГЭ встречаются выпуклые четырехугольники, поэтому подробно изучим их.

Смежные стороны – соседние стороны, которые выходят из одной вершины. Пары смежных сторон: A B и A D , A B и B C , B C и C D , C D и A D .

Противолежащие стороны – несмежные стороны (соединяют разные вершины). Пары противолежащих сторон: A B и C D , B C и A D .

Противолежащие вершины – вершины, не являющиеся соседними (лежат друг напротив друга). Пары противолежащих вершин: A и C , B и D .

Диагонали четырехугольника – отрезки, соединяющие противолежащие вершины. A C и B D – диагонали четырехугольника A B C D .

Диагонали выпуклого четырехугольника пересекаются в одной точке.

Площадь произвольного выпуклого четырехугольника можно найти по формуле:

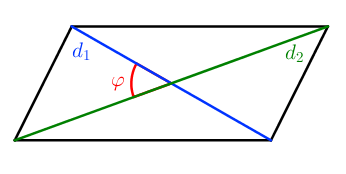
S = 1 2 d 1 d 2 ⋅ sin φ

где d 1 и d 2 – диагонали четырехугольника, φ – угол между диагоналями (острый или тупой – не важно).

Рассмотрим более подробно некоторые виды выпуклых четырехугольников.

Класс параллелограммов: параллелограмм, ромб, прямоугольник, квадрат.

Класс трапеций: произвольная трапеция, прямоугольная трапеция, равнобокая (равнобедренная) трапеция.

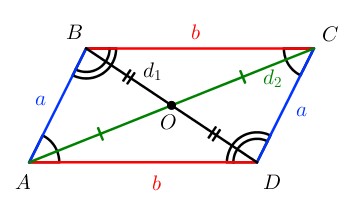
Параллелограмм

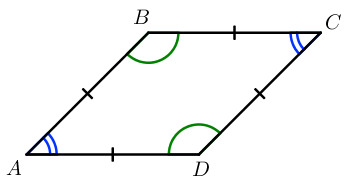
Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.

Свойства параллелограмма:

Противолежащие стороны равны.
Противоположные углы равны.
Диагонали точкой пересечения делятся пополам.
Сумма углов, прилежащих к одной стороне, равна 180 ° .
Сумма квадратов диагоналей равна сумме квадратов сторон. d 1 2 + d 2 2 = 2 ( a 2 + b 2 )

Площадь параллелограмма можно найти по трём формулам.

S = a ⋅ h a = b ⋅ h b

Как произведение стороны и высоты, проведенной к ней.

Поскольку стороны имеют разные длины, то высоты, которые к ним проведены, тоже будут иметь разные длины.

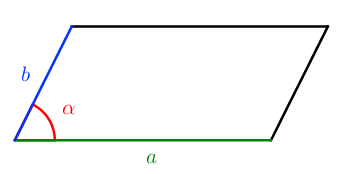
S = a ⋅ b ⋅ sin α

Как произведение двух смежных (соседних) сторон на синус угла между ними.

S = 1 2 ⋅ d 1 ⋅ d 2 ⋅ sin φ

Как полупроизведение диагоналей на синус угла между ними.

Ромб

Ромб – параллелограмм, у которого все стороны равны.

Свойства ромба:

Диагонали пересекаются под прямым углом.
Диагонали являются биссектрисами углов, из которых выходят.
Сохраняются все свойства параллелограмма.

Площадь ромба можно найти по трём формулам.

S = a ⋅ h

Как произведение стороны ромба на высоту ромба.

S = a 2 ⋅ sin α

Как квадрат стороны ромба на синус угла между двумя сторонами.

S = 1 2 ⋅ d 1 ⋅ d 2

Как полупроизведение диагоналей ромба.

Прямоугольник

Прямоугольник – это параллелограмм, у которого все углы равны 90 ° .

Свойства прямоугольника:

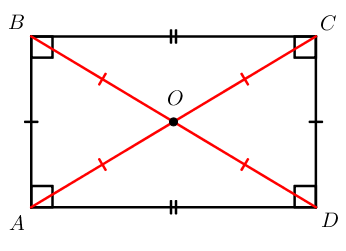
Диагонали прямоугольника равны.
Сохраняются все свойства параллелограмма.

Площадь прямоугольника можно найти по двум формулам:

S = a ⋅ b

Как произведение двух смежных (соседних) сторон прямоугольника.

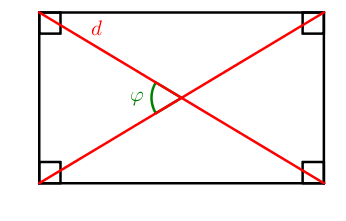
S = 1 2 ⋅ d 2 ⋅ sin φ

Как полупроизведение диагоналей (так как они обе равны, обозначим их буквой d ) на синус угла между ними.

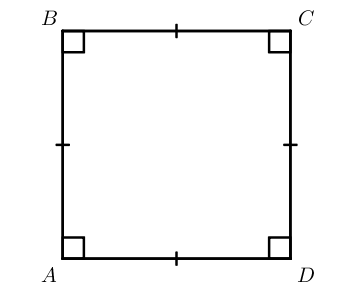
Квадрат

Квадрат – прямоугольник, у которого все стороны равны.

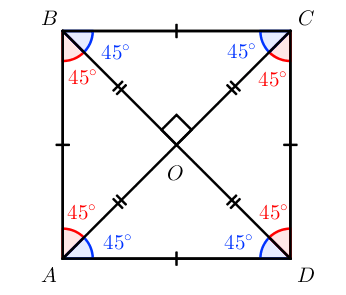
Свойства квадрата:

Сохраняет свойства ромба.
Сохраняет свойства прямоугольника.

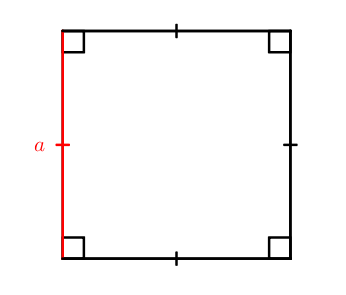
Площадь квадрата можно вычислить по двум формулам:

S = a 2

Как квадрат стороны.

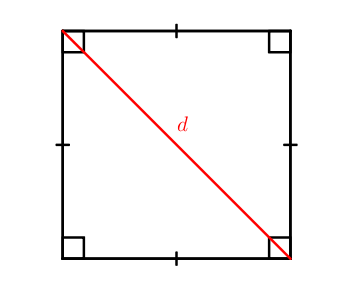
S = d 2 2

Как полупроизведение квадратов диагоналей (диагонали в квадрате равны).

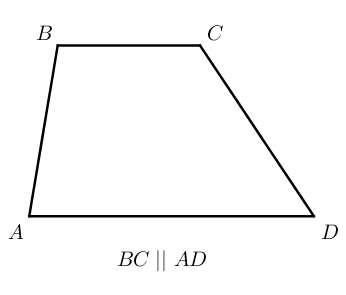
Трапеция

Трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет.

Стороны, которые параллельны друг другу называются основаниями, другие две стороны называются боковыми сторонами.

B C и A D – основания, A B и C D – боковые стороны трапеции A B C D .

Свойства трапеции:

сумма углов, прилежащих к боковой стороне, равна 180 ° .

∠ A + ∠ B = 180 °

∠ C + ∠ D = 180 °

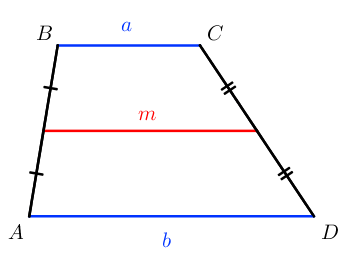
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Средняя линия параллельна основаниям. Её длина находится по формуле: m = a + b 2

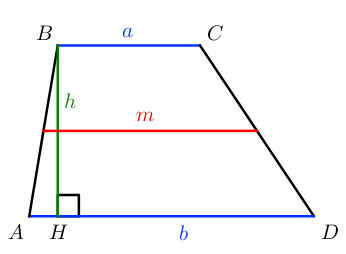
Площадь трапеции можно найти по двум формулам:

S = a + b 2 ⋅ h = m ⋅ h

Как полусумму оснований на высоту. Поскольку полусумма оснований есть средняя линия трапеции, можно найти площадь трапеции как произведение средней линии на высоту.

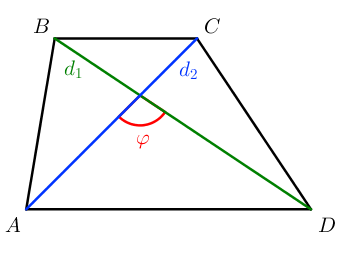
S = 1 2 d 1 ⋅ d 2 ⋅ sin φ

Как полупроизведение диагоналей на синус угла между ними.

Виды трапеций

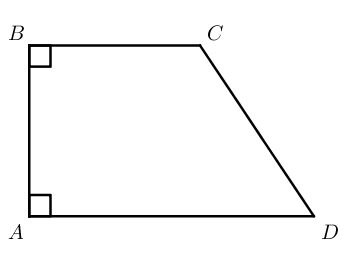
Прямоугольная трапеция – трапеция, у которой два угла прямые.

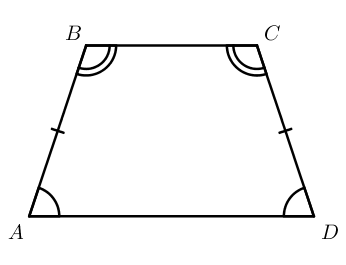
Равнобокая (равнобедренная) трапеция – трапеция, у которой боковые стороны равны.

Свойство равнобокой трапеции: углы при основании равны

Примеры решений заданий из ОГЭ

Модуль геометрия: задания, связанные с четырехугольниками

Скачать домашнее задание к уроку 4.

Источник

Глава
I

1.1.Четырехугольники.

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из
четырёх точек (вершин), не лежащих на одной прямой, и четырёх отрезков
(сторон), попарно соединяющих эти точки. Различают выпуклые и невыпуклые
четырёхугольники.

ЧЕТЫРЁХУГОЛЬНИКИ

┌─────────────┼────────────┐

Невыпуклый
выпуклый самопересекающийся

┌─────────────┼─────────────┐

описанная окружность трапеция
касательный

| ┌───────────┤
|

равнобедренная трапеция параллелограмм
выпуклый ромб

1.
Параллелограмм — четырёхугольник, у которого все
противоположные стороны попарно параллельны;

o Прямоугольник —
четырёхугольник, у которого все углы прямые;

o Ромб —
четырёхугольник, у которого все стороны равны;

o Квадрат —
четырёхугольник, у которого все углы прямые и все стороны равны;

2.
Трапеция — четырёхугольник, у которого две противоположные
стороны параллельны;

3.
Дельтоид — четырёхугольник, у которого две пары смежных
сторон равны.

4.
Выпуклый и невыпуклый четырёхугольники.

Четырёхугольник
называется выпуклым, если он лежит по одну сторону от любой прямой, проходящей
через любые две его смежные вершины. В противном случае четырёхугольник
называется невыпуклым. Диагонали выпуклого четырёхугольника лежат внутри него и
пересекаются. Одна из диагоналей невыпуклого четырёхугольника лежит снаружи, а
другая внутри него, и эти диагонали не пересекаются.

1.2.Площадь
четырехугольников.

Можно
найти площадь четырехугольника по этой формуле по диагоналям.

1.3. Основные
формулы площадей.

Через диагонали и
угол между ними.

Формула для
нахождения площади четырехугольников через диагонали и угол между ними:

Формула
для нахождения площади четырехугольников через диагонали и угол между ними:

)

d1, d2 —
диагонали; α — угол между диагоналями

Через
стороны и противолежащие углы.

Формула
для нахождения площади четырехугольников через стороны и противолежащие углы:

p=

p — полупериметр четырехугольника; a,
b, c, d — стороны четырехугольника; α, β —
противолежащие углы.

Площадь описанного четырехугольника около
окружности через радиус

Формула для
нахождения площади описанного четырехугольника около окружности через радиус:

S=pr

p — полупериметр четырехугольника; r —
радиус вписанной окружности; a, b, c, d — стороны
четырехугольника.

Формула площади квадрата

Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.

S = a²

Формула
площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.

где S — Площадь квадрата,
a —
длина стороны квадрата,
d —
длина диагонали квадрата.

Формула площади прямоугольника

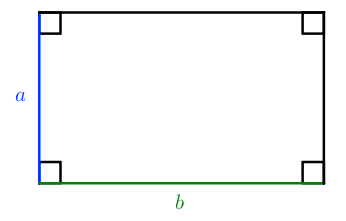
Площадь прямоугольника равна произведению длин двух его смежных сторон

S = a · b

где S — Площадь прямоугольника,
a, b — длины сторон прямоугольника.

Формулы
площади параллелограмм

Формула площади параллелограмма по длине стороны
и высоте
Площадь параллелограмма равна произведению длины его стороны и
длины опущенной на эту сторону высоты.

S = a · h

Формула
площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон
умноженному на синус угла между ними.

S = a · b · sin α

Формула
площади параллелограмма по двум диагоналям и углу между ними
Площадь параллелограмма равна половине произведения длин его
диагоналей умноженному на синус угла между ними.

где S — Площадь параллелограмма,
a, b —
длины сторон параллелограмма,
h —
длина высоты параллелограмма,
d₁, d₂ —
длины диагоналей параллелограмма,
α —
угол между сторонами параллелограмма,
γ —
угол между диагоналями параллелограмма.

Формулы площади ромба

Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины
опущенной на эту сторону высоты.

S = a · h

Формула
площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и
синуса угла между сторонами ромба.

S = a² · sin α

Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей.

где S — Площадь ромба,
a —
длина стороны ромба,
h —
длина высоты ромба,
α —
угол между сторонами ромба,
d₁, d₂ —
длины диагоналей.

Формулы трапеции

Формула Герона для трапеции

S =	a + b	√(p — a)(p — b)(p — a — c)(p — a — d)
\|a — b\|

Формула
площади трапеции по длине основ и высоте
Площадь трапеции равна произведению полусуммы ее оснований на
высоту

где S
— Площадь трапеции,
a, b —
длины основ трапеции,
c, d —
длины боковых сторон трапеции,

p =	a + b + c + d	— полупериметр трапеции

Формулы площади выпуклого четырехугольника

Формула площади четырехугольника по длине
диагоналей и углу между ними
Площадь выпуклого четырехугольника равна половине произведения его
диагоналей умноженному на синус угла между ними:

где S — площадь четырехугольника,
d₁, d₂ —
длины диагоналей четырехугольника,
α —
угол между диагоналями четырехугольника.
Формула площади описанного четырехугольника (по
длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению
полупериметра на радиус вписанной окружности

S = p · r

Формула площади четырехугольника по длине
сторон и значению противоположных углов

S = √(p — a)(p — b)(p — c)(p — d) — abcd cos²θ

где S — площадь четырехугольника,
a, b, c, d —
длины сторон четырехугольника,

p =	a + b + c + d	— полупериметр четырехугольника,
2

θ =	α + β	— полусумма двух противоположных углов четырехугольника.
2

Формула площади четырехугольника, вокруг которого
можно описать окружность

S = √(p — a)(p — b)(p — c)(p — d)

Источник

Если на плоскости последовательно начертить несколько отрезков так, чтобы каждый следующий начинался в том месте, где закончился предыдущий, то получится ломаная линия. Эти отрезки называют звеньями, а места их пересечения — вершинами. Когда конец последнего отрезка пересечется с начальной точкой первого, то получится замкнутая ломаная линия, делящая плоскость на две части. Одна из них является конечной, а вторая бесконечной.

Простая замкнутая линия вместе с заключенной в ней частью плоскости (той, которая конечна) называют многоугольником. Отрезки являются сторонами, а образованные ими углы — вершинами. Количество сторон любого многоугольника равно числу его вершин. Фигура, которая имеет три стороны, называется треугольником, а четыре — четырехугольником. Многоугольник численно характеризуется такой величиной, как площадь, которая показывает размер фигуры. Как найти площадь четырехугольника? Этому учит раздел математики — геометрия.

Чтобы найти площадь четырехугольника, нужно знать к какому типу он относится — выпуклому или невыпуклому? Выпуклый многоугольник весь лежит относительно прямой (а она обязательно содержит какую-либо из его сторон) по одну сторону. Кроме того, есть и такие виды четырехугольников, как параллелограмм с попарно равными и параллельными противоположными сторонами (разновидности его: прямоугольник с прямыми углами, ромб с равными сторонами, квадрат со всеми прямыми углами и четырьмя равными сторонами), трапеция с двумя параллельными противоположными сторонами и дельтоид с двумя парами смежных сторон, которые равны.

Площади любого многоугольника находят, применяя общий метод, который заключается в том, чтобы разбить его на треугольники, для каждого вычислить площадь произвольного треугольника и сложить полученные результаты. Любой выпуклый четырехугольник делится на два треугольника, невыпуклый — на два или три треугольника, площадь его в этом случае может складываться из суммы и разности результатов. Площадь любого треугольника вычисляют как половину произведения основания (a) на высоту (ħ), проведенную к основанию. Формула, которая применяется в этом случае для вычисления, записывается как: S = ½ • a • ħ.

Как найти площадь четырехугольника, например, параллелограмма? Нужно знать длину основания (a), длину боковой стороны (ƀ) и найти синус угла α, образованного основанием и боковой стороной (sinα), формула для расчета будет выглядеть: S = a • ƀ • sinα. Так как синус угла α есть произведение основания параллелограмма на его высоту (ħ = ƀ) — линию перпендикулярная основанию, то его площадь вычисляют, умножив на высоту его основание: S = a • ħ. Для расчета площади ромба и прямоугольника также подходит эта формула. Так как у прямоугольника боковая сторона ƀ совпадает с высотой ħ, то его площадь вычисляют по формуле S = a • ƀ. Площадь квадрата, потому что a = ƀ, будет равняться квадрату его стороны: S = a • a = a². Площадь трапеции вычисляется как половина суммы его сторон, умноженная на высоту (она проводится к основанию трапеции перпендикулярно): S = ½ • (a + ƀ) • ħ.

Как найти площадь четырехугольника, если неизвестны длины его сторон, но известны его диагонали (e) и (f), а также синус угла α? В этом случай площадь вычисляют, как половину произведения его диагоналей (линии, которые соединяют вершины многоугольника), умноженное на синус угла α. Формула может быть записана в таком виде: S = ½ • (e • f) • sinα. В частности площадь ромба в этом случае будет равняться половине произведения диагоналей (линии, соединяющие противоположные углы ромба): S = ½ • (e • f).

Как найти площадь четырехугольника, который не является параллелограммом или трапецией, его обычно принято называть произвольный четырехугольник. Площадь такой фигуры выражают через его полупериметр (Ρ — сумма двух сторон с общей вершиной), стороны a, ƀ, c, d и сумму двух противоположных углов (α + β): S = √[( Ρ – a) • (Ρ – ƀ) • (Ρ – c) • (Ρ – d) – a • ƀ • c • d • cos² ½ (α + β)].

Если четырехугольник вписан в окружность, а φ = 180о, то для расчета его площади используют формулу Брахмагупты (индийский астроном и математик, живший в 6—7 веках нашей эры): S = √[( Ρ – a) • (Ρ – ƀ) • (Ρ – c) • (Ρ – d)]. Если четырехугольник описан окружностью, то (a + c = ƀ + d), а его площадь вычисляют: S = √[ a • ƀ • c • d] • sin ½ (α + β). Если четырехугольник одновременно является описанным одной окружностью и вписанным в другую окружность, то для вычисления площади используют следующую формулу: S = √[a • ƀ • c • d].

Источник