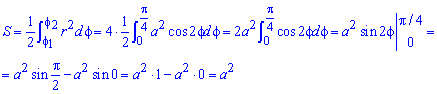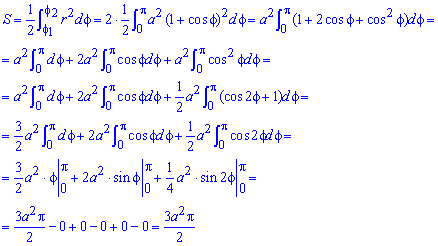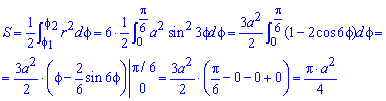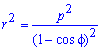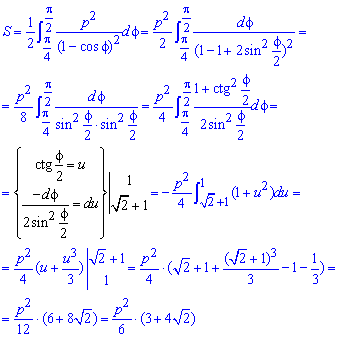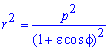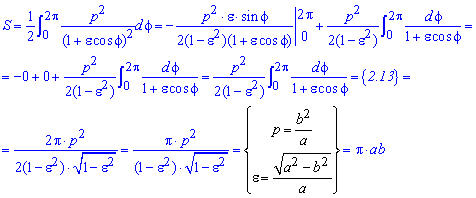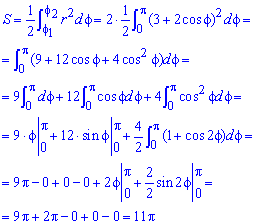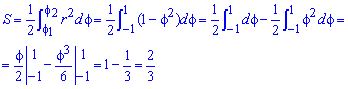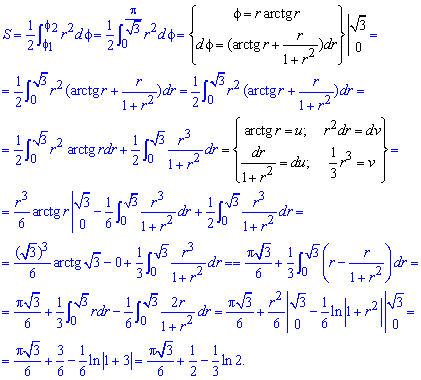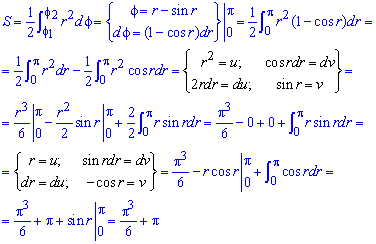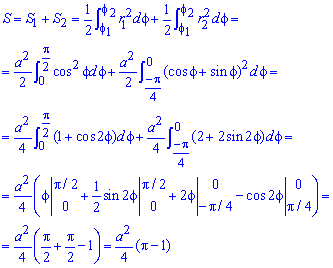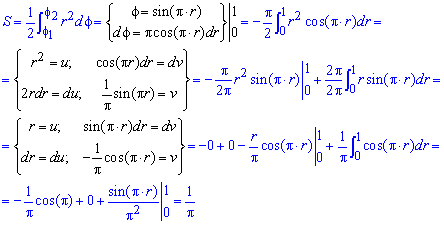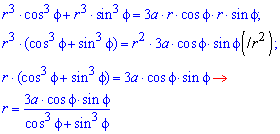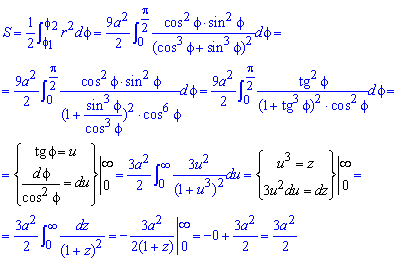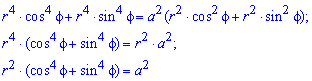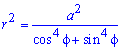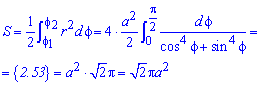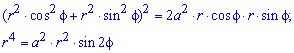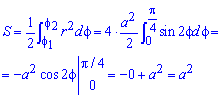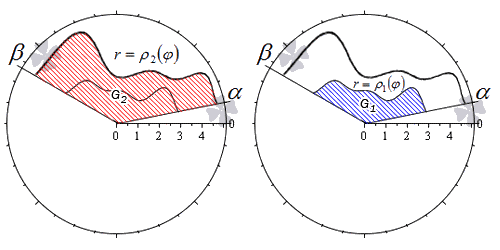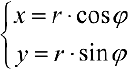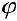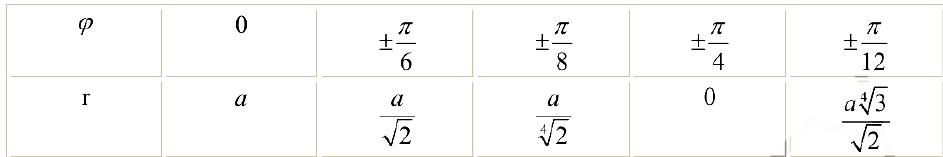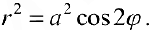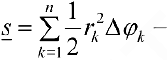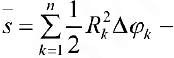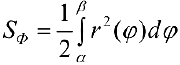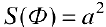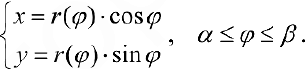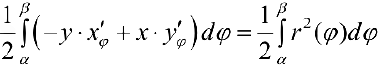|
23:44 площадь фигуры в полярных координатах |
|
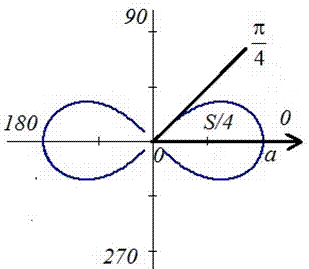
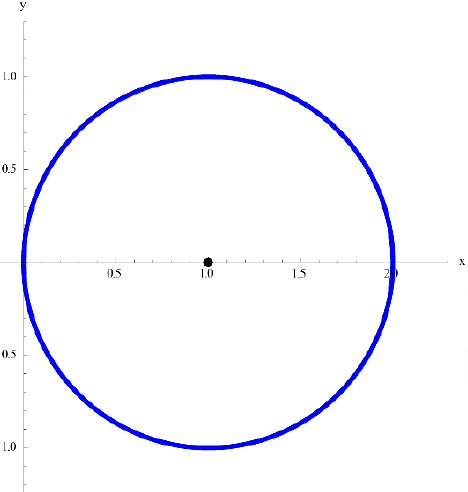
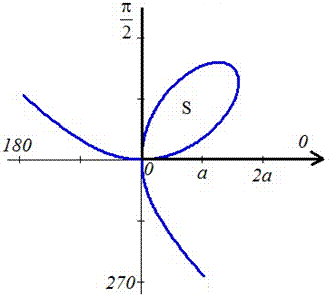
Площадь фигуры, заданной в полярных координатах Рассмотрим примеры вычисления площади фигуры, заданной в полярных координатах кривой ρ= ρ(φ), с помощью определенного интеграла по формуле Пример 1. Вычислить площадь, ограниченную одним лепестком розы Решение. Шаг 1. Выполним рисунок графика функции Шаг 2. Из рисунка видно, что угол φ в первой четверти изменяется от 0 до π/2, следовательно границы интегрирования φ1=0, φ2=π/2 Шаг 3. Уравнение кривой получаем площадь фигуры: Замечание. Вычислить площадь фигуры в полярных координатах можно с помощью калькулятора |
Категория: Площадь фигуры ограниченной кривыми | Просмотров: 45334 | | Теги: площадь фигуры ограниченной линиями | Рейтинг: 3.0/2 |
Лекция 19 Приложение определенного
интеграла. Площадь, длина кривой.
П.1 ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ.
ОПР. Площадью фигуры Ф называют число
,
которое не больше, чем площадь
объемлющей элементарной фигуры
,
например, составленных из многоугольников,
и не меньше, чем площадь
любой объемлемой элементарной фигуры
.
Поскольку
,
следует считать, что площадь имеет та
фигура, для которой
.
ОПР. Криволинейной трапецией называют
фигуру на плоскости, ограниченную осью
ОХ,
прямыми с уравнениями
и
и кривой графика функции
,
определенной на отрезке
.
Пусть
разбиение отрезка
.
В качестве объемлющей фигуры
для
криволинейной трапеции выбираем также
криволинейную трапецию, построенной
для
кусочно-постоянной функции

Аналогично, объемлемой фигурой
для
криволинейной трапеции будем считать
криволинейную трапецию, построенную
для кусочно-постоянной функции
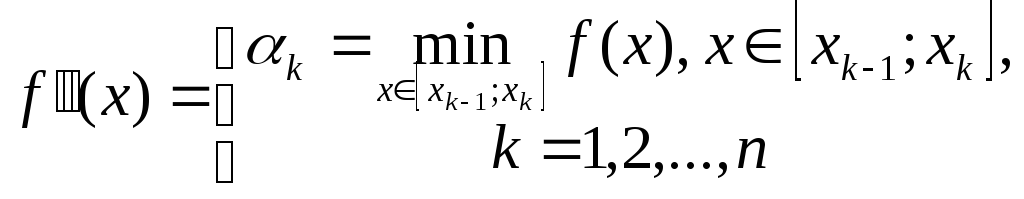
Тогда
и
.
Выражения для
и
являются интегральными суммами ( верхняя
и нижняя интегральные суммы Дарбу) .
Если разбиение
,
то сумма
убывает,
а
—
возрастает. Если функция
интегрируема, то
=
.
Если
на отрезке
,
то площадь криволинейной трапеции равна
—
.
Если функция меняет знак на отрезке
,
то на отрезках , где
интеграл берется со знаком +, а на отрезках
, где
,
интеграл берется со знаком — .
ОПР. Элементарной областью
на плоскости называют фигуру,
ограниченную
прямыми с уравнениями
и
,
графиками непрерывных функций
и
,
ОПР. Элементарной областью
на плоскости называют фигуру, ограниченную
прямыми с уравнениями
и
,
графиками непрерывных функций
и
,
.
ФОРМУЛЫ ВЫЧИСЛЕНИЯ ПЛОЩАДЕЙ фигур
и
.
и
.
ДОК. Если
и
— криволинейные трапеции , соответствующие
функциям
и
на отрезке
и
,
то
.
Тогда

Если
,
но
на некоторых промежутках, то существует
число
,
для которого для функций
и
выполняется условие
.
Площади элементарных фигур, построенных
для функций
и
на
отрезке
равны, т.е.
.
Формула для площади фигуры
доказывается
аналогично. Площадь имеют фигуры,
являющиеся конечным объединением
элементарных областей типа
и
.
ПРИМЕР 1. Площадь сектора окружности
радиуса r с углом
.
РЕШЕНИЕ.
.
Если граница криволинейной трапеции
задается параметрически ,
,
—
возрастающая функция,
,
,
.
Тогда
.
Действительно, по доказанному
.
П 2. Вычисление площади в полярной системе
координат.
ОПР. Элементарной областью
на плоскости называют фигуру, ограниченную
лучами
и
,
кривой
.
ФОРМУЛА ВЫЧИСЛЕНИЯ ПЛОЩАДИ в полярной
системе координат.
Если функция
непрерывна на отрезке
,
то площадь области
вычисляется по формуле :

ДОК. Пусть
— разбиение отрезка
.
Пусть
и
. Тогда объемлющей фигурой для
является элементарная
область,
ограниченная кусочно-постоянной функцией
и
лучами
и
,
имеющая площадь
. Объемлемой фигурой для
является элементарная область
ограниченная кусочно-постоянной функцией
и
лучами
и
,
имеющая площадь
. Числа
и
являются интегральными суммами функции
на отрезке
(верхняя и нижняя интегральные суммы
Дарбу, см. Пример 1). Если
разбиение
,
то сумма
убывает,
возрастает.
Если функция
интегрируема на отрезке
,
то

ПРИМЕР 2. Найти площадь одного лепестка
кривой
( m – лепестковая роза).
РЕШЕНИЕ.
.
.
П.2 ДЛИНА ДУГИ КРИВОЙ.
ОПР. Дуга кривой
разбивается точками
,
на n сегментов, концы
которых
соединены отрезками
.,образующими
ломанную линию
.
Ее длина
зависит от дуги кривой и разбиения
кривой
точками
,
.
Длиной кривой
называют число, равное
,
если оно существует.
Рассмотрим дугу графика функции
на отрезке
.
Каждому разбиению
отрезка
соответствует
ломаная,
состоящая из объединения отрезков с
началом в точках
и
концом в точке,
.
Длина
ломанной
равна
,
где
и
Если функция
имеет
непрерывную производную на отрезке
,
то по теореме Лагранжа существует набор
точек
,
для которых
.
Тогда длина ломанной
является интегральной суммой непрерывной
функции
и поэтому
=
.
ФОРМУЛА ВЫЧИСЛЕНИЯ ДЛИНЫ ДУГИ, заданной
параметрически.
Если дуга кривой задана параметрическими
уравнениями
,
,
в которых функции
имеют
непрерывные производные, то
.
Для ее доказательства заметим, что
разбиение
порождает разбиение дуги кривой точками
и
длину
ломанной
,
где
и
.По
теореме о среднем для производной
существует набор
и
точек на отрезках
,
для которых
и
.
Тогда длина ломаной равна
.
Полученное выражение по форме отличается
от интегральной суммы функции
,
поскольку наборы
и
,вообще
говоря , различные.
Если
интегральная сумма функции
на отрезке
соответствующая
разбиению
,то
.
Для любого
.
Вторая часть оценки использует «
неравенство треугольника»
.
В предположении непрерывности производных
и
колебания
и
—
бесконечно малые функции в точке
,
поэтому существует
такое
, что
для любых
.
Тогда для разбиений
.
ФОРМУЛА ВЫЧИСЛЕНИЯ ДЛИНЫ ДУГИ, заданной
в полярной системе.
Если
,
—
уравнение кривой в полярной системе
координат, то
. Тогда
и
.
Вычислим
и получим искомую формулу

ПРИМЕР 3. (длина цепной линии)
Вычислить длину дуги, заданной уравнением
.
РЕШЕНИЕ.
.
УПРАЖНЕНИЕ. Область ограничена графиком
непрерывно дифференцируемой функции
и прямой , проходящей через точки
и
(сегмент криволинейной трапеции ).
Доказать, что ее площадь
.
РЕШЕНИЕ.
,
где
.
Тогда
,
где
—
функция колебания для производной
на
отрезке
.
Из предположения о непрерывности
следует,
что
.
ВОПРОСЫ К ЭКЗАМЕНУ.
1. Доказательство формулы для вычисления
площади криволинейной трапеции.
2. Доказательство формулы для вычисления
площади фигуры, ограниченной кривой,
заданной параметрически. Вычисление
площади фигуры, граница которой задана
уравнением в полярной системе
координат.
3. Длина дуги кривой заданной графиком
функции, параметрическими уравнениями,
уравнением кривой в полярной системе.
Соседние файлы в папке Лекции по мат. анализу
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Площадь S криволинейного сектора, ограниченного непрерывной кривой r=r(f) и двумя лучами f=f1 и f=f2, где f1<f2 равняется половине определенного интегралу от квадрата радиуса кривой, проинтегрированного в пределах изменения угла
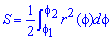
Для запоминания основных моментов схема интегрирования и нахождения площадей из примера в пример будет повторяться. Сами ррешеня по возможности будут проиллюстрированы графиками исследуемых кривых.
Найти площади фигур, ограниченных кривыми, заданными в полярных координатах
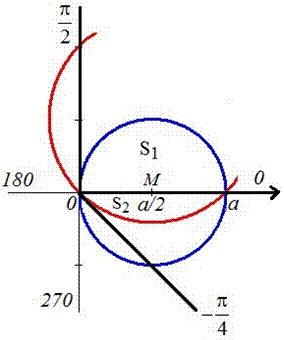
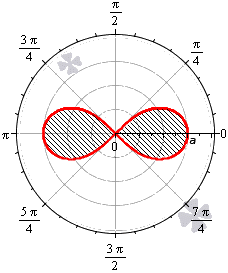
Пример 2.106 (2418) Вычислить площадь фигуры, ограниченной кривыми r2=a2*cos(2f) (лемниската Бернулли).
Вычисление: Лемниската Бернулли — геометрическое место точек, произведение расстояний от которых до двух фиксированных точек (фокусов) остается постоянным и равняется квадрату половины расстояния между фокусами.
Запишем подинтегральную функцию: r2=a2*cos(2f) (известна за условием).
Найдем пределы интегрирования:
задана кривая замкнутая, симметричная относительно прямых r*cos(f)=0 и r*sin(f)=0.
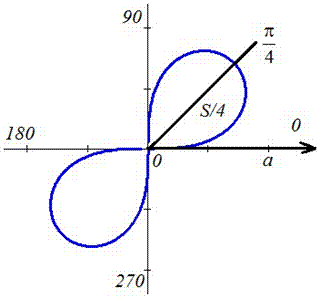
Наведем график лемнискаты Бернулли
Поскольку заданная функция осями координат делится на четыре равных части и достигает своих критических значений при f1=0 (r=a) и f2=p/4 (r=0), то площадь фигуры вычислим для одной части лемнискаты, а результат умножим на 4.
Найдем площадь фигуры интегрированиям по углу
Площадь измеряется в единицах квадратных, однако в этом и следующих примерах размерности наводить не будем, хотя о них помним.
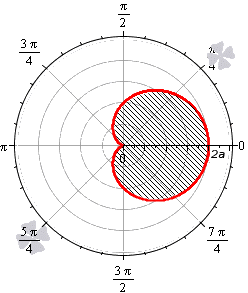
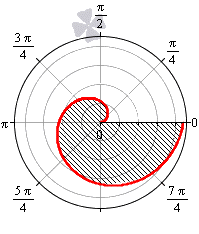
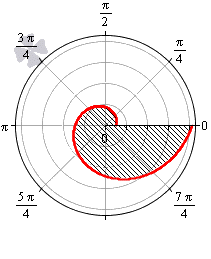
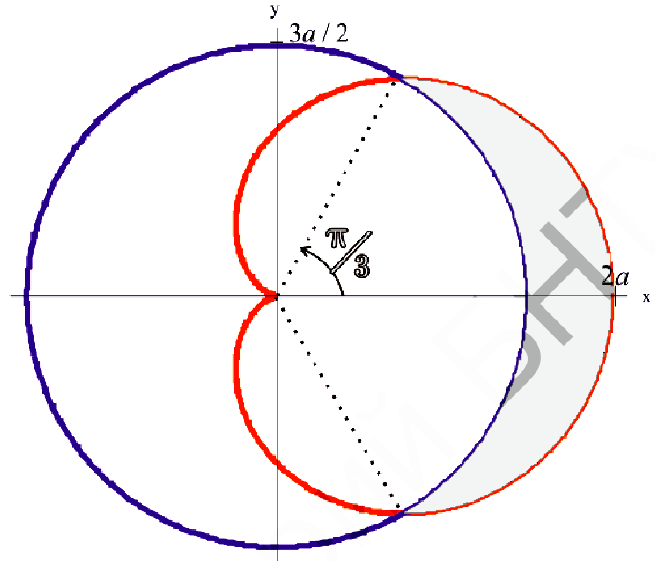
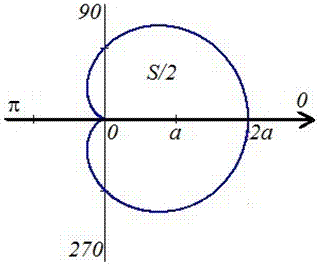
Пример 2.107 (2419) Найти площадь фигуры, ограниченной кривыми r=a* (1+cos(f)) — кардиоида.
Вычисление: Кардиоида — плоская линия, которая описывается фиксированной точкой круга, который катится по неподвижному кругу с таким же радиусом a.
Записываем подинтегральную функцию: r2=a2*(1+cos(f))2.
Находим пределы интегрирования: кривая замкнутая, симметричная относительно прямой r*sin(f) =0.
Поскольку заданная функция осями координат делится на две равных части и достигает своих критических значений при f1=0 (r=2a) и f2=p (r=0), то площадь фигуры вычислим для половины кардиоиды, а результат умножим на 2.
График кардиоиды имеет вид
Вычислим площадь фигуры, которая ограничена заданной кривой, интегрированием:
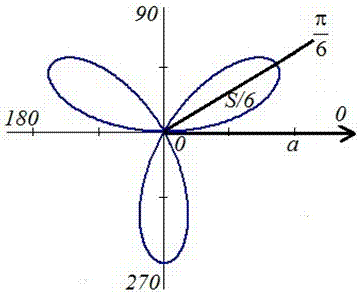
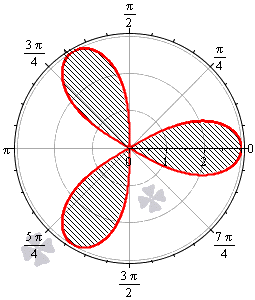
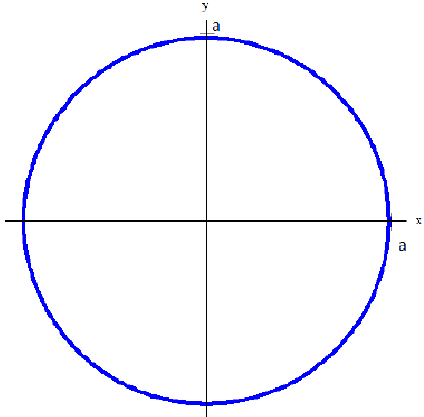
Пример 2.108 (2420) Найти площадь фигуры, ограниченной кривой r=a*sin(f) -трилисник.
Вычисление: Подносим функцию к квадрату, чтобы получить подинтегральную функцию:
r2=a2*sin2(f).
График трилистника в полярной системе координат
Установим пределы интегрирования:
Поскольку заданный график функции делится на шесть равных частей (полупелюсток) и достигает своих критических значений при f1=0 (r=0) и f2=p/6 (r=a/2) то площадь фигуры вычислим для одной его части, а результат умножим на 6.
Находим площадь фигуры интегрированием по углу
Получили простую для вычислений формулу площади трилистника S=Pi*a2/4.
Пример 2.109 ( 2421) Вычислить площадь фигуры, ограниченной кривой 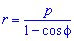
Вычисление: Подносим к квадрату уравнения кривой в полярной системе коринат (СК).
Пределы интегрирования известны f1=p/4, f2=p/2 за условием.
График фигуры, площадь которой нужно найти имеет вид
Интегрированием вычисляем площадь фигуры, которая ограничена параболой:
Для вычисления интеграла следует выполнить замену переменных, не забывая при этом , что изменяются пределы интегрирования.
Пример 2.110 ( 2422) Найти площадь фигуры, ограниченной кривой 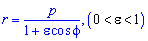
Вычисление: Запишем подинтегральную функцию:
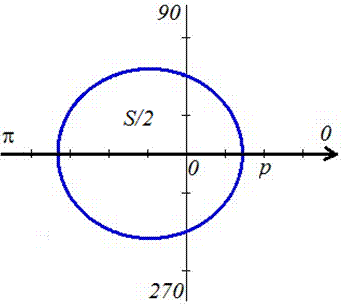
Пределы интегрирования: f1=0, f2=2p (начало и конец кривой эллипса).
График эллипса имеет вид
Находим площадь елипса, воспользовавшись следующей формулой интегрирования
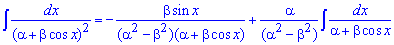
При выведении этой формулы пользовались методом интегрирования частями!
Напоследок превращаем конечную формула с помощью известных формул.
Как видим, ответы задач 2.110 и 2.87 совпадают, то есть площадь эллипса S=Pi*a*b вычислена правильно.
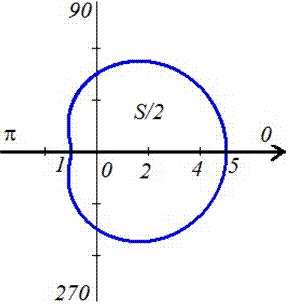
Пример 2.111 (2422.1) Найти площадь фигуры, ограниченной кривой заданной в полярных координатах r=3+2*cos(f).
Вычисление: Сначала находим подинтегральную функцию: r2=(3+2*cos(f))2.
Дальше пределы интегрирования: задана кривая замкнутая, симметричная относительно прямой r*sin(f)=0.
Ее график приведен на рисунку ниже
Поскольку задана кривая осями координат делится на две равных части и достигает своих критических значений при углах f1=0 (r=5) и f2=p (r=1), то вычислим половину площади фигуры, а результат умножим на 2.
Находим площадь фигуры через определенный интеграл
Интеграл в данном случае не тяжелый и, возведя в квадрат подинтегральную функцию и понизив квадрат косинуса, в результате вычислений получим, что площадь равна S=11*Pi.
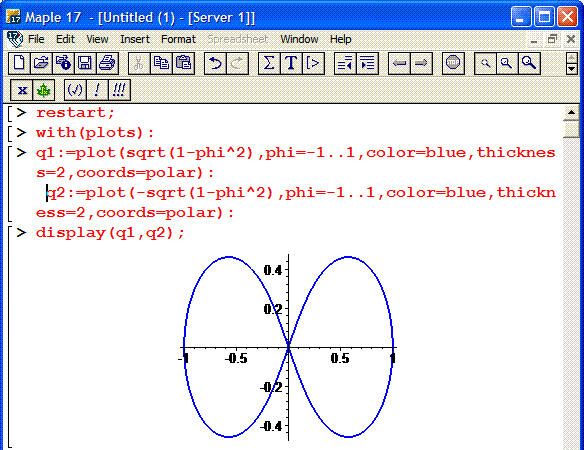
Пример 2.112 (2424.1) Найти площадь фигуры, ограниченной кривой заданной в полярных координатах r2+f2=1.
Вычисление: Выражаемый подинтегральную функцию: r2=1-f2 .
Найдем пределы интегрирования.
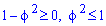
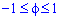
Построим график кривой в математическом пакете Maple17.
Кривая состоит из двух веток корневой функции, поэтому для корректного ее отображения используем следующий код:
> restart;
> with (plots) :
> q1:=plot(sqrt(1-phi^2),phi=-1.1, color=blue, thickness=2, coords=polar):
q2:=plot(-sqrt(1-phi^2),phi=-1.1, color=blue, thickness=2, coords=polar):
> display (q1, q2);
Фрагмент программы Maple приведен ниже
Находим площадь фигуры, которая ограничена кривой:
Интеграл в этом задании простей всех, что рассматривались.
Пример 2.113 ( 2422.2) Вычислить площадь фигуры, ограниченной кривыми 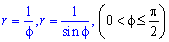
Вычисление: Выписываем подинтегральные функции:
Поскольку на промежутке интегрирования 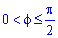
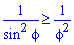
Найдем пределы интегрирования: f1=0 — особенная точка (функция направляется к безграничности) f1=p/2 (известны за условием).
Находим площадь фигуры через предел от интеграла:
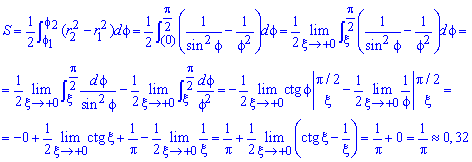
Данный пример хорошо разберите, чтобы не иметь трудностей на экзамене или модуле с подобными.
Пример 2.114 ( 2424) Вычислить площадь фигуры, ограниченной кривой 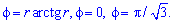
Вычисление: Запишем подинтегральную функцию: r2.
Запишем пределы интегрирования:
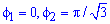
График функций имеет вид
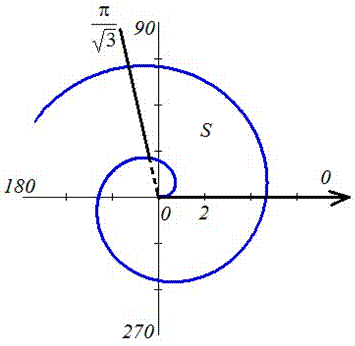
Вычислим площадь фигуры, что приведена на графике.
Для этого сначала находим дифференциал угла f и переходим к интегрированию по радиусу.
Для нахождения интеграла применяем интегрирование частями
Интеграл достаточно трудно находится, поэтому все что содержит формула внимательно проанализируйте.
Пример 2.116 (2424.4) Найти площадь фигуры, ограниченной полярными кривыми f=r-sin(r), f=p.
Вычисление: Подинтегральную функция следующая: r2.
Пределы интегрирования: f1=0, (r=0) начало; f1=p (известно за условием).
График функции имеет вид
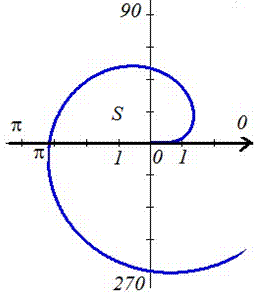
Находим площадь фигуры, применяя дважды интегрирование частями
Интеграл не слишком сложен, все переходы просьба проанализировать самостоятельно.
Пример 2423 Вычислить площадь фигуры, ограниченной полярными кривыми r=a*cos(f), r=a(cos(f)+sin(f)), M (a/2;0)єS.
Вычисление: Для представления фигуры, площадь которой нужно найти предварительно выполняем построение графика заданных функций
Поскольку точка M (a/2;0)єS делит искомую площадь на две части, то имеем два интеграла
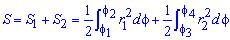
Записываем уравнение подинтегральных функций:
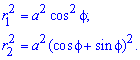
Определяем пределы интегрирования:
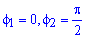
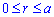
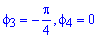
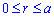
Вычисляем площадь изображенной фигуры интегрированием
Здесь воспользовались известные тригонометрические формулы для понижения степени косинусов и синусов под интегралом. Все остальное сводятся к применению простых формул интегрирования, и нахождения их значений.
Пример 2424.2 Найти площадь фигуры, ограниченной полярными кривыми f=sin(p*r), r пренадлежит [0;1].
Вычисление: Запишем подинтегральную функцию: r2.
Запишем пределы интегрирования: При росте r от 0 к 1/2 угол f растет от 0 к 1, при росте r от 1/2 к 1 угол f спадает от 1 к 0, поэтому величина интеграла в пределах r пренадлежит [0;1] имеет знак «минус».
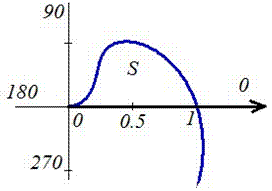
Находим площадь фигуры, предварительно перейдя к новой переменной под интегралом:
Перед интегралом (после замены переменных) поставили знак «минус», поскольку интеграл является отрицательным на этом промежутке, а площадь должна быть положительной.
Перейти к полярным координатам и найти площади фигур, ограниченных кривыми
Пример 2426 Перейти к полярным координатам и найти площадь фигуры x3+y3=3a*x*y (лист Декарта)
Вычисление: Перейдем от прямоугольной системы координат к полярной системе координат за формулами перехода:
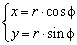
При подстановке в уравнение получим
Поднесем к квадрату, чтобы получить подинтегральную функцию:
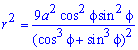
Выпишем пределы интегрирования:
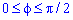
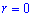
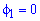
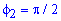
График функции имеет вид
Найдем площадь фигуры интегрированиям:
Для получения конечной формулы площади дважды применяли замену переменных под интегралом.
Внимательно разберите, как при этом изменяются пределы и эффективность методики.
Пример 2427 Перейти к полярным координатам и найти площадь фигуры x4+y4=3a2(x2+y2)
Вычисление: Переходим от прямоугольной к полярной системе координат:
Выражаемый подинтегральную функцию делением:
Запишем пределы интегрирования:
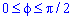
Ее график изображен на рисунку
Оси прямоугольной системы координат являются осями симметрии для фигуры, которая ограничена заданной линией, поэтому площадь найдем для симметричной части и результат умножим на 4.
Находим площадь фигуры через интеграл:
Пример 2428 Перейти к полярным координатам и найти площадь фигуры (x2+y2)2=2a2*x*y (лемниската).
Вычисление: Выполняем переход от прямоугольной к полярной системе координат:
График исследуемой кривой следующий
Запишем пределы интегрирования: учитывая симметрию точек лемнискаты относительно прямой r*sin(f) =r*cos (f) и относительно начала координат, то площадь фигуры будем искать в пределах 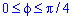
Находим площадь фигуры интегрированием:
Вычислений в этом задании минимум.
В следующих публикациях Вы найдете больше примеров на применение определенного интеграла при вычислении длины дуги, объемов фигур вращения и площадей поверхностей.
Вычисление площади фигуры в полярных координатах
В этом разделе мы продолжим разбирать тему вычисления площадей плоских фигур. Рекомендуем тем, кто изучает темы не по порядку, сначала обратиться к статье «Геометрический смысл определенного интеграла» и разобрать способы вычисления площади криволинейной трапеции. Нам понадобится вычислять площади фигур, которые ограничены ограничены линиями y = f ( x ) , x = g ( y ) в прямоугольной системе координат. А также раздел «Свойства площади фигур», где была разобрана квадрируемость плоских фигур.
Краткий обзор статьи
- Начнем с определения понятия криволинейного сектора, получим формулу для вычисления его площади. Для этого мы используем понятие определенного интеграла Дарбу.
- Подробно разберем решения задач с использованием таких кривых как кардиоида, архимедова спираль и лемниската Бернулли.
- В отдельную подтему мы выделили нахождение площади фигуры, которая представлена как разность двух криволинейных секторов.
Полярная система координат и криволинейный сектор
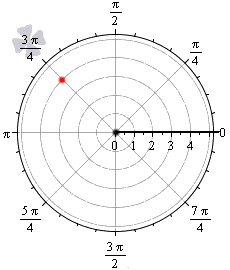
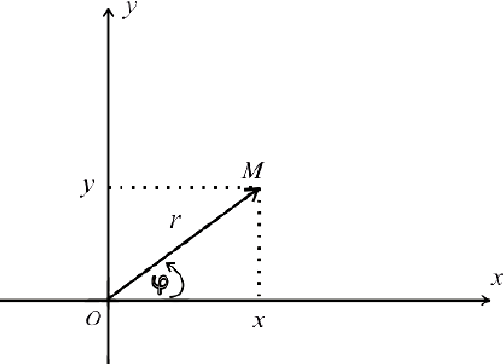
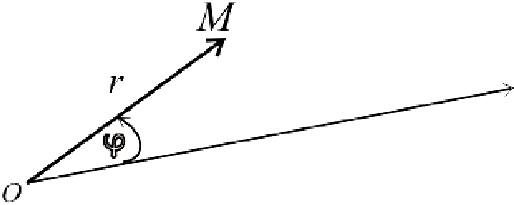
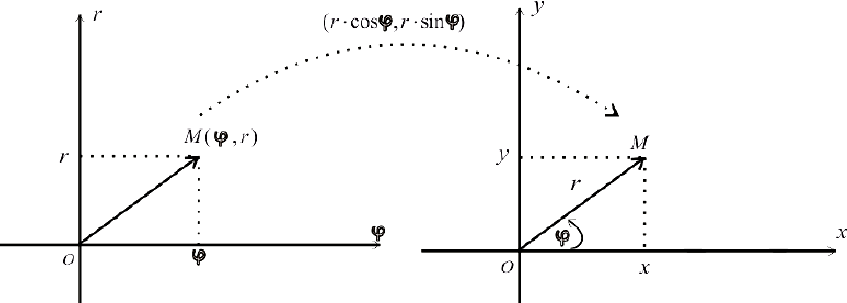
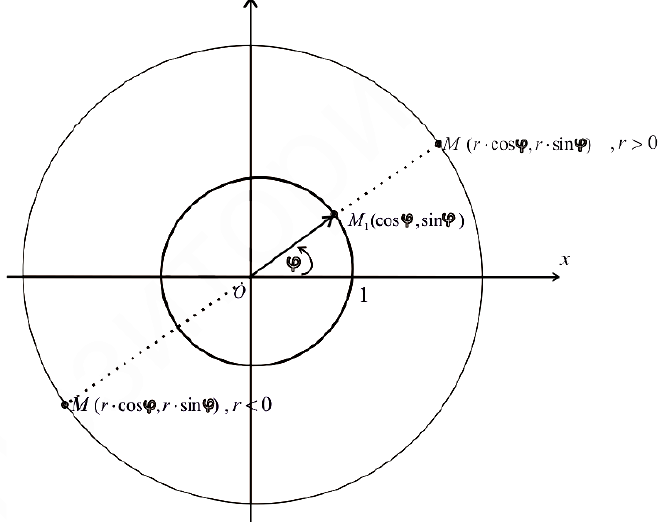
Точка, расположенная в полярной системе координат, имеет полярный угол φ 0 и полярный радиус r 0 ≥ 0 . Полярный угол φ 0 отсчитывается от полярной оси по часовой стрелке, а r 0 — это расстояние от заданной точки до начала координат.
На рисунке мы отметили начало координат (полюс) жирной черной точкой, полярная ось имеет вид луча черного цвета, а красная точка определяется углом φ 0 = 3 π 4 и расстоянием до полюса r 0 = 4 .
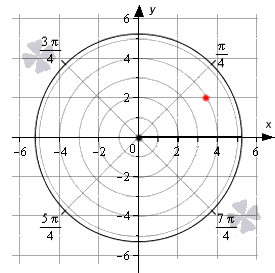
Мы можем рассматривать полярную систему координат одновременно с прямоугольной декартовой. Для этого необходимо совместить начала координат обеих систем, а ось абсцисс и полярной осью.
Задать связь полярных и декартовых координат можно соотношениями r = x 2 + y 2 φ = a r c t g y x , x ≠ 0 и обратно x = r · cos φ y = r · sin φ .
Координаты красной точки на чертеже 2 3 ; 2 . Положение этой точки задается углом φ 0 = a r c t g 2 2 3 = π 6 и расстоянием r 0 = 2 3 2 + 2 2 = 4 .
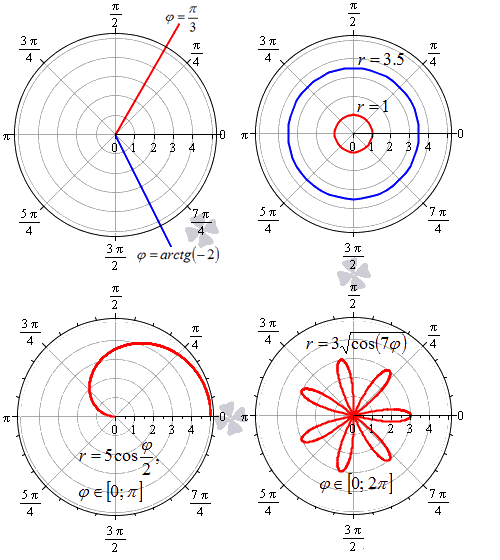
В полярной системе координат равенство φ = α задает луч, который выходит из точки начала координат и составляет угол α с полярной осью. При этом, угол α может быть задан как в радианах, так и в градусах. Полярную ось мы можем задать уравнением вида φ = 0 . Равенство r = C > 0 задает окружность с центром в начале координат, где — это радиус.
Функция r = p ( φ ) , φ ∈ α ; β определяет некоторую линию в полярных координатах.
Следует учитывать тот факт, что с позиции геометрии функция r = p ( φ ) , φ ∈ α ; β во всех случаях будет неотрицательной. Связано это с тем, что она задает расстояние от начала координат до точки для заданного значения угла φ = φ 0 ∈ α ; β . Однако мы будем встречать и отрицательные значения r = p ( φ ) функции, что зависит от отношения к данному вопросу конкретных исследователей и преподавателей.
На рисунке мы изобразили несколько примеров линий в полярной системе координат.
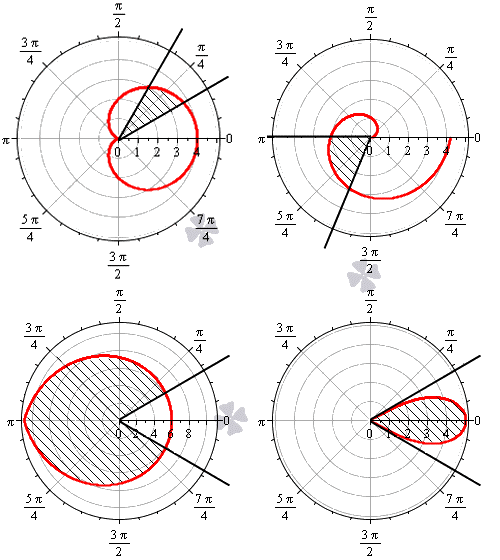
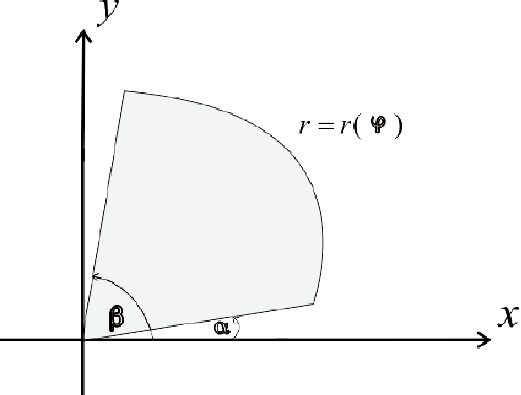
Дадим определение криволинейному сектору.
Криволинейный сектор представляет собой фигуру, которая ограничена лучами φ = α , φ = β и некоторой линией r = p ( φ ) ≥ 0 , непрерывной на участке α ; β .
На рисунке мы привели несколько примеров криволинейных секторов.
На последнем рисунке мы рассмотрели случай, когда фигура располагается между лучами φ = — π 6 , φ = π 6 , которые не являются ее границами.
Площадь криволинейного сектора — вывод формулы
Для вычисления площади криволинейного сектора мы можем вывести формулу. Для этого мы можем использовать формулу площади кругового сектора радиуса R с внутренним углом γ из школьного курса геометрии: S к р у г о в о г о с е к т о р а = γ · R 2 2 . Задаем внутренний угол γ в радианах.
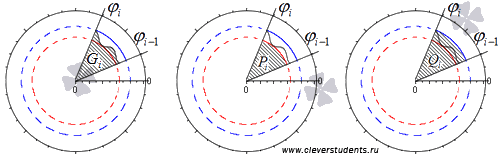
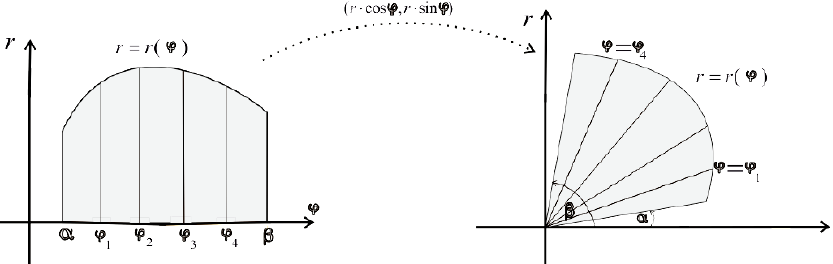
Разобьем криволинейный сектор на n частей такими лучами
φ = φ 1 , φ = φ 2 , . . . , φ = φ n — 1 , что α = φ 0 φ 1 φ 2 . . . φ n — 1 β и λ = m a x i = 1 , 2 , . . . , n φ i — φ i — 1 → 0 при n → + ∞ .
Учитывая свойства площади фигуры, мы можем представить площадь исходного криволинейного сектора S ( G ) как сумму площадей секторов S ( G i ) на каждом из участков разбиения:
S ( G ) = ∑ i = 1 n S ( G i )
Обозначим наибольшее и наименьшее значения функции r = p ( φ ) на i -ом отрезке φ i — 1 ; φ i , i = 1 , 2 , . . . , n как R m i n i и R m a x i . На каждом из отрезков построим по два круговых сектора P i и Q i с максимальным и минимальным радиусами R m i n i и R m a x i соответственно.
Фигуры, которые являются объединением круговых секторов Q i , i = 1 , 2 , . . . , n ; P i , i = 1 , 2 , . . . , n , обозначим как P и Q соответственно.
Их площади будут равны S ( P ) = ∑ i = 1 n S ( P i ) = ∑ i = 1 n 1 2 ( R m i n i ) 2 · φ i — φ i — 1 и S ( Q ) = ∑ i = 1 n S ( Q i ) = ∑ i = 1 n 1 2 ( R m a x i ) 2 · φ i — φ i — 1 , причем S ( P ) ≤ S ( G ) ≤ S ( Q ) .
Так как функция r = p φ непрерывна на отрезке α ; β , то функция 1 2 p 2 φ будет непрерывна на этом отрезке. Если рассматривать S ( P ) и S ( Q ) для этой функции как нижнюю и верхнюю суммы Дарбу, то мы можем прийти к равенству:
lim λ → 0 S ( P ) = lim λ → 0 S ( Q ) = S ( G ) ⇒ S ( G ) = lim λ → 0 ∑ i = 1 n 1 2 ( R m i n i ) 2 · φ i — φ i — 1 = = lim λ → 0 ∑ i = 1 n 1 2 ( R m a x i ) · φ i — φ i — 1 = 1 2 ∫ β α p 2 φ d φ
Формула для определения площади криволинейного сектора имеет вид:
S ( G ) = 1 2 ∫ β α p 2 φ d φ
Примеры вычисления площади криволинейного сектора
Рассмотрим алгоритмы вычисления площади криволинейного сектора с полярной системе координат на конкретных примерах.
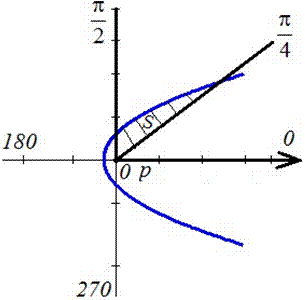
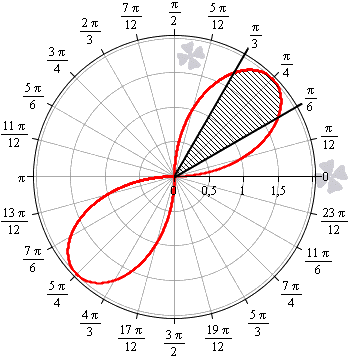
Необходимо вычислить площадь плоской фигуры в полярных координатах, которая ограничена линией r = 2 sin 2 φ и лучами φ = π 6 , φ = π 3 .
Решение
Для начала, изобразим описанную в условии задачи фигуру в полярной системе координат. Функция r = 2 sin ( 2 φ ) положительна и непрерывна на отрезке φ ∈ π 6 , π 3 .
Полученная фигура является криволинейным сектором, что позволяет нам применить формулу для нахождения площади этого сектора.
S ( G ) = 1 2 ∫ π 6 π 3 ( 2 sin ( 2 φ ) 2 d φ = ∫ π 6 π 3 2 ( sin ( 2 φ ) 2 d φ = ∫ π 6 π 3 2 · 1 — cos 4 φ 2 d φ = ∫ π 6 π 3 ( 1 — cos ( 4 φ ) ) d φ = φ — 1 4 sin ( 4 φ ) π 6 π 3 = = π 3 — 1 4 sin 4 π 3 — π 6 — 1 4 sin 4 π 6 = π 6 + 3 4
Ответ: S ( G ) = π 6 + 3 4
Задача упрощается в тех случаях, когда лучи φ = φ 1 , φ = φ 2 , ограничивающие фигуру, заданы. Тогда нам не нужно задумываться о пределах интегрирования при проведении вычисления площади.
Чаще встречаются задачи, где фигуру ограничивает лишь кривая r = p ( φ ) . В этих случаях применить формулу S ( G ) = 1 2 ∫ α β p 2 ( φ ) d φ сразу не получится. Для начала придется решить неравенство p ( φ ) ≥ 0 для нахождения пределов интегрирования. Так мы можем поступить в тех случаях, когда функция r = p φ неотрицательная. В противном случае нам придется ориентироваться только на область определения и период функции.
Необходимо вычислить площадь фигуры, которая ограничена кривой в полярных координатах r = — 3 · cos 3 φ .
Решение
Функция определена для всех действительных значений аргумента. Решим неравенство — 3 · cos 3 φ ≥ 0 :
— 3 · cos 3 φ ≥ 0 ⇔ cos 3 φ ≤ 0 ⇔ cos φ ≤ 0 ⇔ ⇔ π 2 + 2 πk ≤ φ ≤ 3 π 2 + 2 πk , k ∈ Z
Построим функцию в полярных координатах на отрезке φ ∈ π 2 ; 3 π 2 (при k = 0 ). Для других значений k в силу периодичности косинуса мы будем получать ту же самую кривую.
Применим формулу для вычисления площади фигуры в полярных координатах. В качестве нижнего и верхнего предела можно брать π 2 + 2 πk и 3 π 2 + 2 πk соответственно для любого целого значения k .
S ( G ) = 1 2 ∫ π 2 3 π 2 ( — 3 · cos 3 φ ) d φ = 9 2 ∫ π 2 3 π 2 cos 6 φ d φ
Для того, чтобы получить ответ, нам необходимо вычислить полученный определенный интеграл. Для этого мы можем использовать формулу Ньютона-Лейбница. Первообразную для формулы Ньютона-Лейбница мы можем с помощью рекуррентной формулы вида K n ( x ) = sin x · cos n — 1 ( x ) n + n — 1 n K n — 2 ( x ) , где K n ( x ) = ∫ cos n ( x ) d x .
∫ cos 6 φ d φ = sin φ · cos 5 φ 6 + 5 6 ∫ cos 4 φ d φ = = sin φ · cos 5 φ 6 + 5 6 sin φ · cos 3 φ 4 + 3 4 cos 2 φ d φ = = sin φ · cos 5 φ 6 + 5 sin φ · cos 3 φ 24 + 15 24 sin φ · cos φ 2 + 1 2 ∫ cos 0 φ d φ = = ∫ π 2 3 π 2 cos 6 φ d φ = sin φ · cos 5 φ 6 + 5 sin φ · cos 3 φ 24 + 15 sin φ · cos φ 48 + 15 φ 48 π 2 3 π 2 = = 15 48 · 3 π 2 — 15 48 · π 2 = 5 π 16
Таким образом, искомая площадь фигуры, ограниченной линией в полярной системе координат, равна S ( G ) = 9 2 ∫ π 2 3 π 2 cos 6 φ d φ = 9 2 · 5 π 16 = 45 π 32 .
Ответ: S ( G ) = 45 π 32
В тех случаях, когда в полярной системе координат задается множество кривых, которые по форме напоминают листья клевера или цветка, площадь фигур, ограниченных этими кривыми, часто одинаковы. В этих случаях можно вычислить площадь одного «лепестка» и умножить ее на количество криволинейных фигур.
Необходимо вычислить площадь плоской фигуры в полярной системе координат, которая ограничена линией r = 3 · cos ( 3 φ ) .
Решение
Найдем область определения, исходя из того, что эта функция неотрицательна для любого φ из области определения.
cos ( 3 φ ) ≥ 0 ⇔ — π 2 + 2 πk ≤ 3 φ ≤ π 2 + 2 πk , k ∈ Z — π 6 + 2 π 3 k ≤ φ ≤ π 6 + 2 π 3 k , k ∈ Z
Таким образом, период функции r = 3 · cos 3 φ равен 2 π 3 . Это значит, что фигура состоит из трех областей одинаковой площади.
Построим фигуру на графике.
Вычислим площадь одного участка, расположенного на интервале φ ∈ π 2 ; 5 π 6 (при k = 1 ):
1 2 ∫ π 2 5 π 6 9 cos ( 3 φ ) d φ = 1 2 · 3 sin ( 3 φ ) π 2 5 π 6 = 3 2 sin 3 · 5 π 6 — sin 3 · π 2 = 3 2 ( 1 — ( — 1 ) = 3
Ответ: Площадь всей фигуры будет равна площади найденного участка, умноженной на 3.
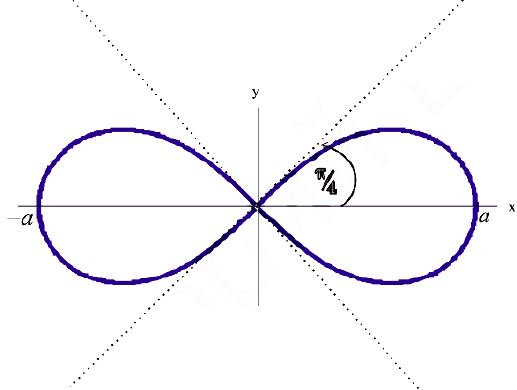
Аналогичным образом можно найти площади фигур, имеющих сходное строение. Примером может служить лемниската Бернулли.
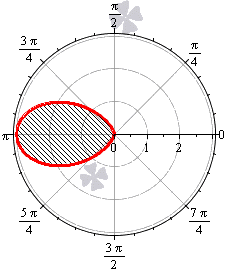
Площадь фигуры, которую ограничивает лемниската Бернулли
Лемниската Бернулли задается уравнением r = α · cos 2 φ где a – положительное число, влияющее на размер линии (но не на конфигурацию, схожую с символом бесконечности). Лемниската Бернулли строится при — π 4 + π · k ≤ φ ≤ π 4 + π · k , k ∈ Z .
Лемниската служит границей фигуры, которую можно представить как два равных по площади участка.
Для вычисления площади используем нужную формулу:
S ( G ) = 2 · 1 2 ∫ — π 4 π 4 a 2 cos ( 2 φ ) 2 φ = a 2 2 ( sin ( 2 φ ) ) — π 4 π 4 = = a 2 2 sin 2 · π 4 — sin 2 · — π 4 = a 2
Получается, что площадь фигуры, которую ограничивает лемниската Бернулли, равна квадрату коэффициента a .
Площадь фигуры, границей которой является кардиоида
В полярной системе координат кардиоида задается уравнением вида r = 2 a ( 1 + cos φ ) . В этом уравнении a – некоторое положительное число. Задающая кардиоиду функция является периодической с периодом 2 π . Она определена для всех действительных значений угла. Это значит, что для вычисления площади нижним пределом интегрирования мы будем считать любое число, а верхним, то, которое на 2 π больше нижнего.
Вычислим площадь фигуры, ограниченной кардиоидой r = 2 a ( 1 + cos φ ) , для φ ∈ 0 ; 2 π :
S ( G ) = 1 2 ∫ 0 2 π ( 2 a ( 1 + cos φ ) ) 2 d φ = 2 a 2 ∫ 0 2 π ( 1 + 2 cos φ + cos 2 φ ) d φ = = 2 a 2 ∫ 0 2 π 1 + 2 cos φ + 1 + cos 2 φ 2 d φ = = 2 a 2 ∫ 0 2 π 3 2 + 2 cos φ + cos ( 2 φ ) 2 d φ = = 2 a 2 3 2 φ + 2 sin φ + 1 4 sin 2 φ 0 2 π = 6 π · a 2
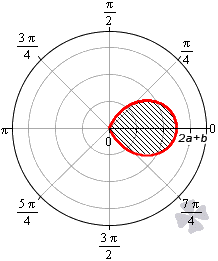
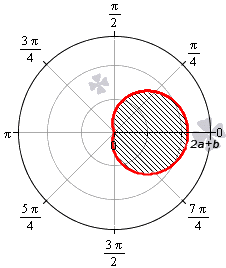
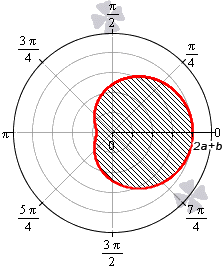
Площадь фигуры, которую ограничивает улитка Паскаля
В полярной системе координат улитка Паскаля может быть задана уравнением r = b + 2 a · cos φ . В этом уравнении a – это некоторое положительное число, b – любое действительное число. Кардиоиду можно рассматривать как частный случай улитки Паскаля. Получить кардиоиду можно при b = 2 a .
Улитка Паскаля в зависимости от значений параметров a и b может принимать различный вид. В данном разделе мы рассмотрим случаи, когда функцию r неотрицательная.
При b — 2 a функция r = b + 2 a · cos φ будет отрицательной для любого значения угла φ .
При b = — 2 a улитка Паскаля имеет вид точки, которая совпадает с полюсом.
При — 2 a b 0 функция r = b + 2 a · cos φ неотрицательна для φ ∈ — a r c cos — b 2 a + 2 πk ; arccos — b 2 a + 2 πk , k ∈ Z .
При 0 b 2 a функция r = b + 2 a · cos φ неотрицательна для φ ∈ — a r c cos — b 2 a + 2 πk ; arccos — b 2 a + 2 πk , k ∈ Z . Она ограничивает фигуру, которая по конфигурации напоминает кардиоиду.
При b > 2 a функция r = b + 2 a · cos φ является неотрицательной для любого значения угла. Графическая иллюстрация этого случая приведена ниже
Для того, чтобы правильно определить пределы интегрирования, необходимо учитывать соотношение параметров a и b .
Необходимы вычислить площадь фигуры, которая ограничена линиями, заданными уравнениями r = — 3 + 6 cos φ и r = 5 + 4 cos φ в полярной системе координат.
Решение
Формула r = — 3 + 6 cos φ соответствует фигуре, известной как улитка Паскаля..
Функция r = — 3 + 6 cos φ определена для всех значений угла φ . Нам необходимо выяснить, при каких φ функция будет неотрицательной:
— 3 + 6 cos φ ≥ 0 ⇔ cos φ ≥ 1 2 ⇔ — π 3 + 2 π k ≤ φ ≤ π 3 + 2 πk , k ∈ Z
Проведем вычисление площади фигуры, которая ограничена данной улиткой Паскаля:
S ( G ) = 1 2 ∫ — π 3 π 3 ( — 3 + 6 cos φ ) 2 d φ = 9 2 ∫ — π 3 π 3 ( 1 — 4 cos φ + 4 cos 2 φ ) d φ = = 9 2 ∫ — π 3 π 3 1 — 4 cos φ + 4 · 1 + cos 2 φ 2 d φ = = 9 2 ∫ — π 3 π 3 ( 3 — 4 cos φ + 2 cos ( 2 φ ) ) d φ = 9 2 · 3 φ — 4 sin φ + sin ( 2 φ — π 3 π 3 = = 9 2 · 3 · π 3 — 4 sin π 3 + sin 2 π 3 — 3 · — π 3 — 4 sin — π 3 + sin — 2 π 3 = = 9 2 · 2 π — 3 3
Улитка Паскаля, определяемая формулой r = 5 + 4 cos φ , соответствует пятому пункту. Функция r = 5 + 4 cos φ определена и положительна для всех действительных значений φ . Поэтому, площадь фигуры в этом случае равна:
S ( G ) = 1 2 ∫ 0 2 π ( 5 + 4 cos φ ) 2 d φ = 1 2 ∫ 0 2 π ( 25 + 40 cos φ + 16 cos 2 φ ) d φ = = 1 2 ∫ 0 2 π 25 + 40 cos φ + 16 · 1 + cos ( 2 φ ) 2 d φ = = 1 2 ∫ 0 2 π ( 33 + 40 cos φ + 8 cos ( 2 φ ) ) d φ = 1 2 · 33 φ + 40 sin φ + 4 sin ( 2 φ 0 2 π = = 1 2 · 33 · 2 π + 40 sin ( 2 π + 4 sin ( 4 π ) — 33 · 0 + 40 sin 0 + 4 sin 0 = 33 π
Ответ: S ( G ) = 33 π
Площадь фигур, границей которых является спираль Архимеда или логарифмическая спираль
Сразу обратимся к примеру.
Необходимо вычислить площадь фигур в полярной системе координат, первая из которых ограничена первым витком спирали Архимеда r = α φ , α > 0 , а вторая первым витком логарифмической спирали r = α φ , α > 1 .
Решение
Если в задаче сказано, что фигура ограничена первым витком спирали Архимеда, то угол φ изменяется от нуля до двух пи.
Исходя из этого, найдем площадь фигуры по формуле:
S ( G ) = 1 2 ∫ 0 2 π ( α φ ) 2 d ϕ = α 2 2 ∫ 0 2 π φ 2 d φ = α 2 2 · φ 3 3 0 2 π = 4 α 3 π 3 3
Аналогично вычисляется площадь фигуры, ограниченной первым витком логарифмической спирали:
S ( G ) = 1 2 ∫ 0 2 π ( α ϕ ) 2 d ϕ = 1 2 ∫ 0 2 π a 2 φ d φ = 1 4 ln a · a 2 φ 0 2 π = = 1 4 ln a · a 4 π — 1
Нахождение площади фигуры, которую можно представить как разность двух криволинейных секторов
Пусть фигура в полярной системе координат ограничена лучами φ = α , φ = β и непрерывными и неотрицательными на интервале φ ∈ α ; β функциями r = p 1 ( φ ) и r = p 2 ( φ ) , причем p 1 ( φ ) ≤ p 2 ( φ ) для любого угла φ = φ 0 ∈ α ; β .
Находим площадь фигуры по формуле S ( G ) = 1 2 ∫ α β p 2 2 ( φ ) — p 1 2 ( φ ) d φ .
Действительно, в силу свойства аддитивности площади, фигуру G можно представить как разность двух криволинейных секторов G 2 и G 1 .
Тогда площадь фигуры G равна разности площадей этих криволинейных секторов:
S ( G ) = S ( G 2 ) — S ( G 1 ) = 1 2 ∫ α β p 2 2 ( φ ) d φ — 1 2 ∫ α β p 1 2 ( φ ) d φ = = 1 2 ∫ α β p 2 2 ( φ ) — p 1 2 ( φ ) d φ
Последний переход возможен в силу третьего свойства определенного интеграла.
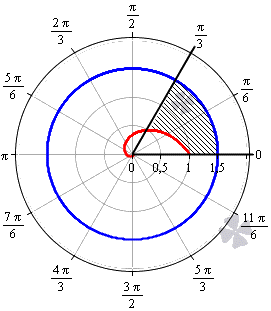
Необходимо вычислить площадь фигуры, которая ограничена линиями φ = 0 , φ = π 3 , r = 3 2 , r = 1 2 φ в полярной системе координат.
Решение
Построим заданную фигуру на графике.
Очевидно, что r = 3 2 больше r = 1 2 φ для любого φ ∈ 0 ; π 3 . Применяем полученную формулу для вычисления площади фигуры:
S ( G ) = 1 2 ∫ 0 π 3 3 2 2 — 1 2 φ 2 d φ = 1 2 ∫ 0 π 3 9 4 — 2 — 2 φ d φ = = 1 2 · 9 4 φ + 1 2 · 2 — 2 φ ln 2 0 π 3 = 1 2 · 9 4 φ + 1 ln 2 · 1 2 2 φ + 1 0 π 3 = = 1 2 · 9 4 · π 3 + 1 ln 2 · 1 2 2 · π 3 + 1 — 9 4 · 0 + 1 ln 2 · 1 2 2 · 0 + 1 = = 1 2 · 3 π 4 + 2 — 2 π 3 — 1 2 · ln 2
Ответ: S ( G ) = 1 2 · 3 π 4 + 2 — 2 π 3 — 1 2 · ln 2
А теперь рассмотрим пример, когда фигура ограничена линиями, заданными в прямоугольной системе координат. Площадь такой фигуры намного проще вычислять, используя полярные координаты.
Необходимо вычислить площадь фигуры, которая ограничена прямыми линиями y = 1 3 x , x = 3 x , окружностями ( x — 2 ) 2 + ( y — 3 ) 2 = 13 , ( x — 4 ) 2 + ( y — 3 ) 2 = 25 .
Решение
В прямоугольной системе координат вычислить площадь полученной фигуры можно, но дело это долгое и хлопотное. Намного проще перейти к полярной системе координат, воспользовавшись формулами перехода.
x = r · cos φ y = r · sin φ ⇒ y = 1 3 x ⇔ r · sin φ = r · cos φ 3 ⇔ t g φ = 1 3 ⇔ φ = π 6 + πk y = 3 x ⇔ r · sinφ = 3 · r · cosφ ⇔ tgφ = 3 ⇔ φ = π 3 + πk ( x — 2 ) 2 + ( y — 3 ) 2 = 13 ⇔ x 2 + y 2 = 4 x + 6 y ⇔ r = 4 cosφ + 6 sinφ ( x — 4 ) 2 + ( y — 3 ) 2 = 25 ⇔ x 2 + y 2 = 8 x + 6 y ⇔ r = 8 cosφ + 6 sinφ
Функция r = 8 cos φ + 6 sin φ больше r = 4 cos φ + 6 sin φ для любого φ ∈ π 6 ; π 3 . Вычисляем площадь фигуры в полярных координатах:
S ( G ) = 1 2 ∫ π 6 π 3 8 cos φ + 6 sin φ 2 — 4 cos φ + 6 sin φ 2 d φ = = 1 2 ∫ π 6 π 3 ( 48 cos 2 φ + 48 cos φ · sin φ ) d φ = = 24 ∫ π 6 π 3 cos 2 φ d φ + 24 ∫ π 6 π 3 cos φ · sin φ d φ = = 12 ∫ π 6 π 3 ( 1 + cos 2 φ ) d φ + 24 ∫ π 6 π 3 sin φ d ( sin φ ) = = 12 · φ + 1 2 sin ( 2 φ ) π 6 π 3 + 12 · sin 2 φ π 6 π 3 = = 12 · π 3 + 1 2 sin 2 π 3 — π 6 + 1 2 sin 2 π 6 + 12 · sin 2 π 3 — sin 2 π 6 = = 12 · π 6 + 12 · 3 2 2 — 1 2 2 = 2 π + 6
Вычислить площади фигур ограниченных линиями заданными уравнениями в полярной системе координат
Запрошуємо усіх хто любить цікаві задачі та головоломки відвідати групу! Зараз діє акція — підтримай студента! Знижки на роботи + безкоштовні консультації.
Контакты
Администратор, решение задач
Роман
Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym
Решение задач
Андрей
facebook:
dniprovets25
Вычисление площадей фигур в различных системах координат
Площадь плоской фигуры в декартовых координатах
Напомним, что мы назвали криволинейной трапецией фигуру, ограниченную осью абсцисс, прямыми и и графиком функции . В этом пункте выведем формулу для вычисления площади криволинейной трапеции.
Теорема 3. Если функция неотрицательна на отрезке и непрерывна на нем, то соответствующая ей криволинейная трапеция квадрируема, причем ее площадь выражается формулой
Доказательство. Криволинейная трапеция ограничена тремя отрезками и графиком непрерывной функции . Как было показано в пункте 2 такая фигура квадрируема. Чтобы вычислить площадь этой трапеции, построим для нее внешние и внутренние ступенчатые фигуры (см. рис. 26).
Тогда, с одной стороны, имеем:
где — площадь внутренней ступенчатой фигуры, —площадь внешней ступенчатой фигуры, и . С другой стороны, по определению интеграла можно записать:
Таким образом, числа и разделяют одни и те же числовые множества: . Но, как было показано при изучении определенного интеграла, эти множества разделяются лишь одним числом, и потому . Теорема доказана.
Аналогично доказывается, что если фигура ограничена снизу графиком функции , сверху графиком функции , а слева и справа прямыми (рис. 30), то ее площадь выражается формулой
Наглядный смысл формулы (4) состоит в том, что криволинейную трапецию можно рассматривать как объединение «бесконечно тонких полосок» с основаниями и высотами .
Пусть теперь функция непрерывна на отрезке и принимает на нем только неположительные значения. Выразим с помощью определенного интеграла площадь соответствующей криволинейной трапеции .
Рассмотрим фигуру , симметричную фигуре относительно оси . Эта фигура (рис. 31) представляет собой криволинейную трапецию, ограниченную сверху графиком непрерывной на отрезке функции , которая на принимает только неотрицательные значения. По доказанному выше
Как мы видим, в рассматриваемом случае интеграл дает значение площади криволинейной трапеции с точностью до знака. Если же функция меняет знак на отрезке в конечном числе точек, то значение интеграла дает алгебраическую сумму площадей соответствующих криволинейных трапеций, ограниченных частями графика функции , отрезками оси и, быть может, отрезками, параллельными оси (рис. 32).
Пример 1. Найти площадь фигуры, ограниченной кривой , осью абсцисс и прямыми (рис. 33).
Решение. Имеем: (кв. ед.).
Пример 2. Вычислить площадь фигуры, ограниченной дугой параболы и отрезком прямой (рис. 34).
Решение. Из рисунка видно, что трапеция, площадь которой нужно найти, расположена симметрично относительно оси абсцисс и, следовательно, искомая площадь равна
Пример 3. Найти площадь фигуры, ограниченной графиками функций (рис. 35).
Решение. Искомая площадь равна разности площадей криволинейного треугольника и прямоугольного треугольника
Пример 4. Вычислить площадь фигуры, ограниченной петлей кривой .
Решение. Из уравнения кривой видно, что она расположена симметрично относительно оси . Следовательно, можно сначала вычислить половину искомой площади (рис. 36). Рекомендуем читателю подробно исследовать и построить данную кривую.
Записав уравнение кривой в виде , найдем точки пересечения ее с осью , положив . Учитывая сказанное, найдем площадь половины петли:
Воспользовавшись формулой из таблицы при , получим:
Значит, окончательно имеем:
Площадь фигуры, ограниченной кривой, заданной параметрически
Пусть кривая задана в параметрической форме
где функция монотонна на отрезке , причем , и имеет на этом отрезке непрерывную производную. Так как , то по формуле замены переменной под знаком определенного интеграла получаем:
Итак, площадь фигуры, ограниченной кривой, заданной параметрически, вычисляется по формуле:
Пример 5. Вычислить площадь эллипса, заданного параметрически
Решение. Выберем ту часть эллипса (рис. 37), которая расположена в первом квадранте. Точке соответствует значение , а точке — значение . Поэтому
Площадь фигуры, заданной в полярных координатах
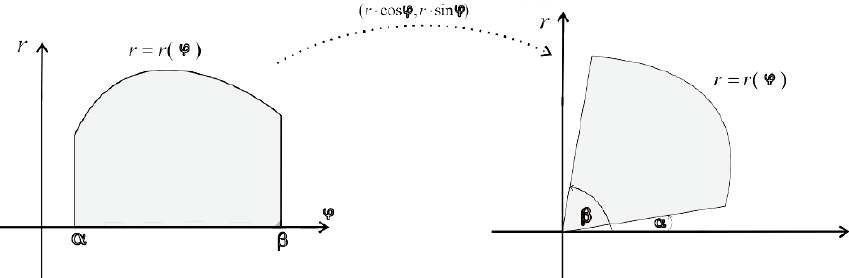
Вычислить площадь сектора, ограниченного лучами и , выходящими из точки , и непрерывной кривой (рис. 38). Выберем полярную систему координат, полюсом которой является точка . Пусть — полярное уравнение кривой , а и — углы между полярной осью и лучами и соответственно. При этом пусть функция непрерывна на .
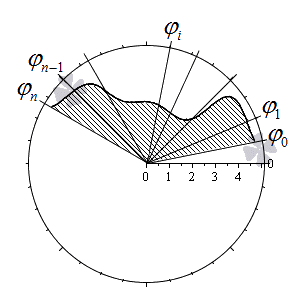
Разобьем данный сектор на частей лучами
и рассмотрим k-й частичный сектор (рис. 39). Пусть — наименьшее значение функции в , a — наибольшее значение функции в этом отрезке.
Построим два круговых сектора с радиусами и . Обозначим через величину угла рассматриваемого частичного сектора. Тогда площадь частичного криволинейного сектора будет заключена между площадями вписанного и описанного частичных круговых секторов
Построим аналогичным образом внутренние и внешние круговые секторы для всех частичных криволинейных секторов. Объединяя их, получим внутреннюю и внешнюю фигуры.
Площадь внутренней фигуры, состоящей из круговых секторов, равна , а площадь внешней фигуры равна — . Эти выражения являются нижней и верхней суммами Дарбу и для интеграла . Так как функция непрерывна, то непрерывна, а потому и интегрируема функция . Поэтому для любого найдется такое разбиение отрезка , что . Из теоремы 2 пункта 2 следует, что заданный криволинейный сектор квадрируем. При этом для его площади выполняются неравенства
В то же время по определению определенного интеграла
В силу единственности разделяющего числа из неравенств (6) и (7) следует, что
Пример 6. Вычислить площадь, ограниченную одним лепестком розы (рис. 40).
Вычисление площади фигуры в полярных координатах с помощью интеграла Текст научной статьи по специальности « Математика»
Аннотация научной статьи по математике, автор научной работы — Махсуд Тулқин Ўғли Усмонов
Это, пожалуй, одно из самых популярных приложений определённого интеграла после вычисления площади в прямоугольных координатах и объёма тела вращения . Ручное построение чертежа в полярных координатах процесс длительный и трудоёмкий.
Похожие темы научных работ по математике , автор научной работы — Махсуд Тулқин Ўғли Усмонов
Текст научной работы на тему «Вычисление площади фигуры в полярных координатах с помощью интеграла»
Вычисление площади фигуры в полярных координатах с
Махсуд Тулкин угли Усмонов maqsudu32@gmail .com Ташкентский университет информационных технологий
Аннотация: Это, пожалуй, одно из самых популярных приложений определённого интеграла после вычисления площади в прямоугольных координатах и объёма тела вращения. Ручное построение чертежа в полярных координатах — процесс длительный и трудоёмкий.
Ключевые слова: определённый интеграл, вычисление площади в прямоугольных координатах, объём тела вращения.
Calculating the area of a figure in polar coordinates using an
Mahsud Tulgin oglu Usmonov maqsudu32@gmail.com Tashkent University of Information Technologies
Abstract: This is perhaps one of the most popular applications of the definite integral after calculating the area in rectangular coordinates and the volume of a body of revolution. Manual construction of a drawing in polar coordinates is a long and laborious process.
Keywords: definite integral, calculation of area in rectangular coordinates, volume of a body of revolution.
Всё очень и очень напоминает привычную задачу нахождения площади. Полярным аналогом криволинейной трапеции является криволинейный сектор.
Рассмотрим некоторую функцию r ^ заданную в полярной системе
координат, которая принимает неотрицательные значения на отрезке ^ е ^ ^ и непрерывна на нём. Криволинейным сектором называется фигура,
ограниченная отрезками лучей Ф
Площадь криволинейного сектора рассчитывается по формуле
2 я . Как видите, перед интегралом ставится дробь 2 , сама функция
возводится в квадрат, а интегрирование осуществляется по переменной «фи».
В качестве демонстрационного примера, вычислим площадь круга, ограниченного окружностью г — 2 с центром в полюсе, радиуса 2. Очевидно, что а = 0> и по формуле:
Вычислить площадь фигуры, ограниченной линией = Ф Ручное построение чертежа в полярных координатах — процесс длительный и трудоёмкий. В нашем случае задача облегчается ещё и тем, что
т = для любого «фи»,
а значит, угол, как и в примере с площадью круга, принимает все значения
от а = 0 д0 2л- до рабочей формуле:
Стандартно понижаем степень с помощью известной тригонометрической формулы:
Забавно, что можно вообще не иметь ни малейшего представления о том,
какую фигуру ограничивает линия г( = J cos2 2 qdq> = 2jcos2 2qdtp—
(*) На данном шаге использовали чётность подынтегральной функции на симметричном относительно нуля отрезке интегрирования. С геометрической точки зрения это означает, что лепесток розы симметричен относительно своей центральной оси. В предыдущих двух примерах фигуры тоже были симметричными, но, как ни странно, в рассматриваемом типе задач излишнее обмусоливание данного факта зачастую только удлиняет решение.
Если считать, что уравнение ‘»‘Ж1 — i::0Sзадано в обобщенных полярных координатах, то данная роза будет иметь 4 лепестка, и, соответственно, результат следует умножить ещё на два. Но, как я уже советовал в курсе аналитической геометрии, осмотрительнее рассматривать классику, где полярный радиус неотрицателен.
Кривая 4-го примера называется лемнискатой Бернулли, в 5-м примере дана трёхлепесковая роза. Напоминаю, что если есть возможность быстро построить чертеж, то его лучше построить. А здесь они, к слову, быстро строятся и вручную.
После интенсивной разминки на опушке надеваем хоккейную маску и с воодушевлением углубляемся в лес за новыми жертвами: Пример 6
Вычислить площадь фигуры, ограниченной линиями r
^ г — 2 sin ^ Решение: в условии даны две линии, и здесь хоть о чертеже и молчок, но
без него уже трудно. Какую кривую задаёт уравнение в статье о
полярных координатах мы подробно разбирали и строили график полярной
розы ^ с лепестками на промежутках
«минус» всё перевернёт с ног на голову (а если академичнее — отобразит симметрично относительно полярной оси и её продолжения) и лепестки розы
расположатся в секторах
2 зт ^ значительно проще, оно определяет типовую окружность:
Y>4 Г = 2 sin Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
3) Площадь искомой фигуры:
Ответ: 3 , что весьма правдоподобно
В рассмотренном примере фигурировали разные отрезки интегрирования,
s = Т. — Г33( , г = sin д>
, не определена однозначно и
поэтому в условии наложено дополнительное ограничение на угол из которого следует, что необходимо вычислить заштрихованную площадь
If ■ a , — sin q>dq>=—
2) На промежутке
фигура ограничена тем же отрезком луча
Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
3. Margulis A. Ya., Andrey Petrovich Kiselev, «Mathematics at school», 1948,
4. Depman I. Ya., History of arithmetic, M., 1959.
5. Morgulis A. Ya., Trostnikov V. Legislator of school mathematics // Science and life. 1968. No. 1
6. Pylnev-Rogachev, Luneva MI Servant of the «queen of sciences» // Koltsovsky square. 2002. No. 3
http://yukhym.com/ru/integrirovanie-funktsii/ploshchad-figury-v-polyarnykh-koordinatakh.html
http://mathhelpplanet.com/static.php?p=ploshchadi-figur-v-razlichnykh-sistemakh-koordinat
http://cyberleninka.ru/article/n/vychislenie-ploschadi-figury-v-polyarnyh-koordinatah-s-pomoschyu-integrala
Полярная система координат
Определение 1. Рассмотрим плоскость с прямоугольной декартовой системой координат 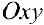
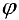
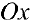
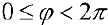
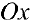
Замечание. Зависимость между прямоугольными 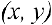
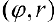
Рис. 1. Полярные координаты точки.
Полярный полюс О и полярную ось можно выбрать на плоскости и не вводя прямоугольную систему координат:
Задача №83
Построим на плоскости линию, заданную уравнением: 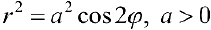
Решение:
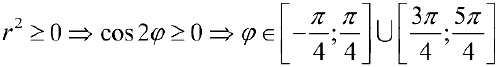
Вычислим значения 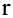
Проводим лучи из начала координат под углами 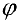
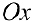
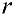
Рис.З. Лемниската
Задача №84
а) Построим кривую 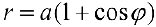
Рис.4. Кардиоида 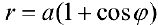
б) 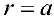
Рис.5. Окружность 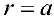
в) 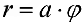
Рис.6. Спираль Архимеда 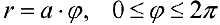
г) 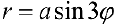
Рис.7. Трехлепестковая роза 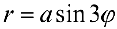
Упражнение 1. Построить графики из примеров 1 и 2 в системе Mathematica (использовать функцию PolarPlot, см.пример 10 § 17).
Замечание. Если в определении 1 отбросить требование 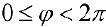
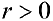
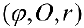
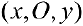
При этом, если 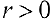
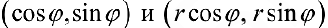
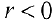
Тогда, с учетом (1), кривую 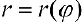
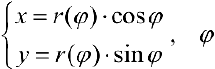
В этом случае па кривой 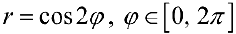
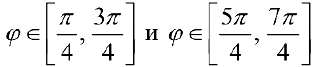
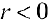
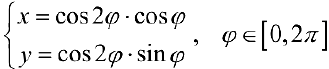
На кривой 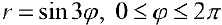
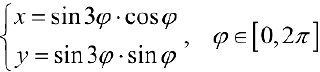
Упражнение 2. Используя команду PolarPlot построить графики 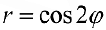
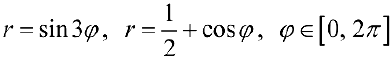
Пусть 

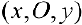
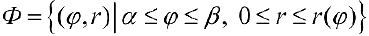
Разобьем фигуру Ф на n частичных фигур лучами 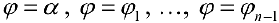
Рассмотрим, например, нижние суммы Дарбу:
Рис.8. Нижняя сумма Дарбу 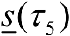
Каждое слагаемое в нижней сумме 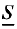
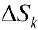
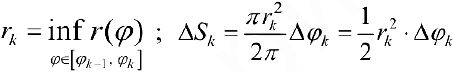
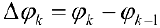
таким образом,
для нижних сумм и
для верхних сумм Дарбу, где 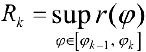
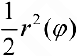
Задача №85
Найти площадь ограниченную лемнискатой 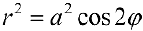
Решение:
По формуле (4):
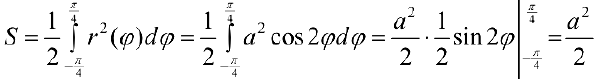
Поэтому
Задача №86
Найти площадь фигуры ограниченной линиями: 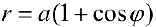
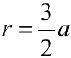
Рис.8. Фигура 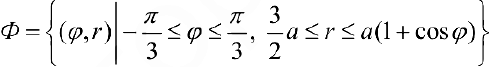
Решение:
Найдем точки пересечения кривых: 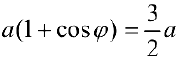
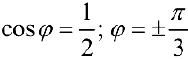
Задача №87
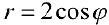
Преобразуем уравнение 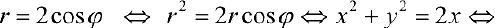
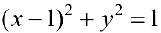
Рис.9. Окружность 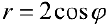
При изменении 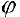
Упражнение 3. Пусть
Проверить, что (см. (7) §30):
Упражнение 4. Используя формулу (4), найти площади фигур, ограниченных линиями: 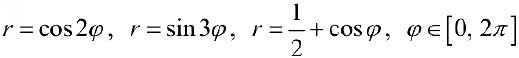
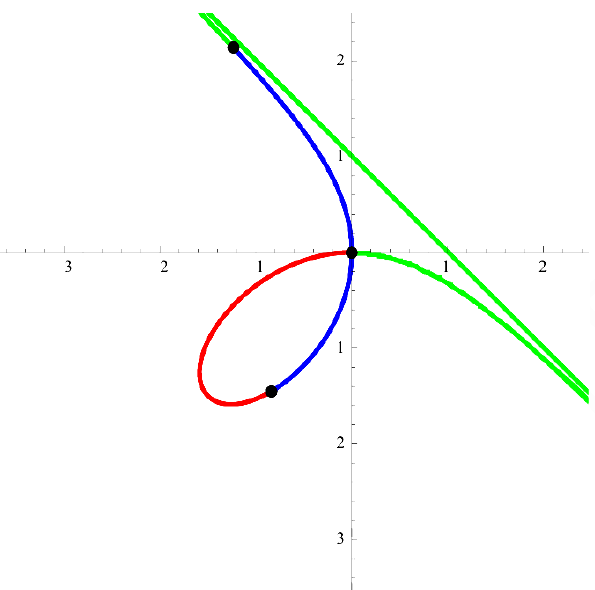
Упражнение 5. Найти площадь петли кривой 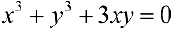
Рис. 10. Кривая 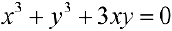
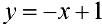
Указание. Перейти в полярную систему координат.
Эта теория и задачи с решением взяты со страницы готовых задач с решением по математическому анализу:
Решение задач по математическому анализу
Возможно эти темы вам будут полезны: