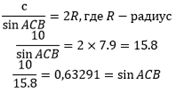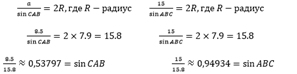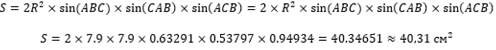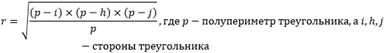Площадь круга: как найти, формулы
О чем эта статья:
площадь, 6 класс, 9 класс, ЕГЭ/ОГЭ
Определение основных понятий
Прежде чем погрузиться в последовательность расчетов и узнать, чему равна площадь круга, важно выяснить разницу между понятиями окружности и круга.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Если говорить простым языком, окружность — это замкнутая линия, как, например, кольцо и шина. Круг — плоская фигура, ограниченная окружностью, как монетка или крышка люка.
Формула вычисления площади круга
Давайте разберем несколько формул расчета площади круга. Поехали!
Площадь круга через радиус
S = π × r 2 , где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Площадь круга через диаметр
S = d 2 : 4 × π, где d — это диаметр.
Площадь круга через длину окружности
S = L 2 : (4 × π), где L — это длина окружности.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Задачи. Определить площадь круга
Мы разобрали три формулы для вычисления площади круга. А теперь тренироваться — поехали!
Задание 1. Как найти площадь круга по диаметру, если значение радиуса равно 6 см.
Диаметр окружности равен двум радиусам.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 12 2 : 4.
Ответ: 113,04 см 2 .
Задание 2. Найти площадь круга, если известен диаметр, равный 90 мм.
Используем формулу: S = π × d 2 : 4.
Подставим известные значения: S = 3,14 × 90 2 : 4.
Ответ: 6358,5 мм 2 .
Задание 3. Найти длину окружности при радиусе 3 см.
Отношение длины окружности к диаметру является постоянным числом.
Получается: L = d × π.
Так как диаметр равен двум радиусам, то формула длины окружности примет вид: L = 2 × π × r.
Подставим значение радиуса: L = 2 × 3,14 × 3.
Ответ: 18,84 см 2 .
Треугольник вписанный в окружность
Определение
Треугольник, вписанный в окружность — это треугольник, который
находится внутри окружности и соприкасается с ней всеми тремя вершинами.
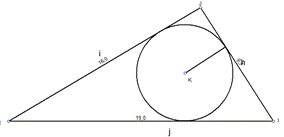
На рисунке 1 изображена окружность, описанная около
треугольника и окружность, вписанная в треугольник.
ВD = FC = AE — диаметры описанной около треугольника окружности.
O — центр вписанной в треугольник окружности.
Формулы
Радиус вписанной окружности в треугольник
r — радиус вписанной окружности.
- Радиус вписанной окружности в треугольник,
если известна площадь и все стороны:
Радиус вписанной окружности в треугольник,
если известны площадь и периметр:
Радиус вписанной окружности в треугольник,
если известны полупериметр и все стороны:
Радиус описанной окружности около треугольника
R — радиус описанной окружности.
- Радиус описанной окружности около треугольника,
если известна одна из сторон и синус противолежащего стороне угла:
Радиус описанной окружности около треугольника,
если известны все стороны и площадь:
Радиус описанной окружности около треугольника,
если известны все стороны и полупериметр:
Площадь треугольника
S — площадь треугольника.
- Площадь треугольника вписанного в окружность,
если известен полупериметр и радиус вписанной окружности:
Площадь треугольника вписанного в окружность,
если известен полупериметр:
Площадь треугольника вписанного в окружность,
если известен высота и основание:
Площадь треугольника вписанного в окружность,
если известна сторона и два прилежащих к ней угла:
Площадь треугольника вписанного в окружность,
если известны две стороны и синус угла между ними:
[ S = frac<1><2>ab cdot sin angle C ]
Периметр треугольника
P — периметр треугольника.
- Периметр треугольника вписанного в окружность,
если известны все стороны:
Периметр треугольника вписанного в окружность,
если известна площадь и радиус вписанной окружности:
Периметр треугольника вписанного в окружность,
если известны две стороны и угол между ними:
Сторона треугольника
a — сторона треугольника.
- Сторона треугольника вписанного в окружность,
если известны две стороны и косинус угла между ними:
Сторона треугольника вписанного в
окружность, если известна сторона и два угла:
Средняя линия треугольника
l — средняя линия треугольника.
- Средняя линия треугольника вписанного
в окружность, если известно основание:
Средняя линия треугольника вписанного в окружность,
если известныдве стороны, ни одна из них не является
основанием, и косинус угламежду ними:
Высота треугольника
h — высота треугольника.
- Высота треугольника вписанного в окружность,
если известна площадь и основание:
Высота треугольника вписанного в окружность,
если известен сторона и синус угла прилежащего
к этой стороне, и находящегося напротив высоты:
[ h = b cdot sin alpha ]
Высота треугольника вписанного в окружность,
если известен радиус описанной окружности и
две стороны, ни одна из которых не является основанием:
Свойства
- Центр вписанной в треугольник окружности
находится на пересечении биссектрис. - В треугольник, вписанный в окружность,
можно вписать окружность, причем только одну. - Для треугольника, вписанного в окружность,
справедлива Теорема Синусов, Теорема Косинусов
и Теорема Пифагора. - Центр описанной около треугольника окружности
находится на пересечении серединных перпендикуляров. - Все вершины треугольника, вписанного
в окружность, лежат на окружности. - Сумма всех углов треугольника — 180 градусов.
- Площадь треугольника вокруг которого описана окружность, и
треугольника, в который вписана окружность, можно найти по
формуле Герона.
Доказательство
Около любого треугольника, можно
описать окружность притом только одну.
окружность и треугольник,
которые изображены на рисунке 2.
окружность описана
около треугольника.
- Проведем серединные
перпендикуляры — HO, FO, EO. - O — точка пересечения серединных
перпендикуляров равноудалена от
всех вершин треугольника. - Центр окружности — точка пересечения
серединных перпендикуляров — около
треугольника описана окружность — O,
от центра окружности к вершинам можно
провести равные отрезки — радиусы — OB, OA, OC.
окружность описана около треугольника,
что и требовалось доказать.
Подводя итог, можно сказать, что треугольник,
вписанный в окружность — это треугольник,
в котором все серединные перпендикуляры
пересекаются в одной точке, и эта точка
равноудалена от всех вершин треугольника.
Быстро найти формулу для расчета онлайн.
Условие задачи:
Прямоугольный треугольник АВС вписан в окружность Найти площадь круга, ограниченного этой окружностью, если размер клеток составляет 1см на 1см.
Дано:
Размер клетки, = 1 см на 1 см
Пояснение к рисунку:
O — центр окружности
К — вершина прямого угла, достроенного прямоугольного треугольника
D — диаметр описанной окружности
c — гипотенуза треугольника
Найти площадь круга: S
Суть всего решения сводится к тому, что:
— первое , достроенный треугольник АСК, имеет смежную гипотенузу с треугольником АВС и является также вписанным в окружность и прямоугольным. А у этого треугольника мы можем уже точно определить его катеты АК=13клеток=13см и КС=5клеток=5см.
— второе , как известно, если прямоугольный треугольник вписан в окружность, то его гипотенуза равна диаметру окружности. Это так же видно и из чертежа.
Для определения площади круга, используем следующую формулу через диаметр, который необходимо найти.
А как уже было сказано выше, диаметр окружности равен гипотенузе.
По теореме Пифагора, находим гипотенузу, т. е. диаметр окружности.
Подставляем полученное выражение в формулу площади круга.
Вставляем значения и вычисляем результат.
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
http://colibrus.ru/treugolnik-vpisannyy-v-okruzhnost/
http://www-formula.ru/81-zadachi/area/list-circle/circle
Условие задачи:
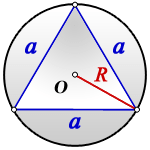
Равносторонний треугольник со стороной 1 м вписан в окружность. Найти площадь круга, ограниченного этой окружностью.
Дано:
Сторона треугольника, a = 1 м
Пояснение к рисунку:
O — центр окружности
R — радиус описанной окружности
Найти площадь круга: S
Решение
Используем формулу площади круга через радиус. Но пока он нам не известен, его надо найти.
Определить радиус, нам поможет следующая формула. В ней радиус окружности выражен через сторону вписанного треугольника.
Подставим радиус выраженный через сторону и преобразовав, получим следующие выражение.
Подставим значения.
Результат получился приблизительным, потому что число π нельзя выразить точно, оно имеет бесконечное количество знаков после запятой. В данном случаи, мы взяли π ≈ 3.14
Ответ:
Калькулятор для расчета площади круга
- Подробности
-
Опубликовано: 15 сентября 2017
-
Обновлено: 13 августа 2021
Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.
Содержание
- Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
- Формула нахождения площади круга через радиус:
- Формула нахождения S-площади круга через D-диаметр:
- Нахождение S круга, если известна длина окружности:
- Площадь круга, вписанного в квадрат: формула, примеры решения задач
- Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
- Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
- Площадь круга, описанного около квадрата: формула, примеры решения задач
- Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
- Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
- Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
- Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
- Видео: Математика | Вычисление площадей круга и его частей
Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.
Площадь круга: формула через радиус, диаметр, длину окружности, примеры решения задач
Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.
Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.
Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.
Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.
Формула нахождения площади круга через радиус:
Примеры решения заданий по нахождению S-площади круга через R-радиус:
————————————————————————————————————————
Задача: Найдите площадь окружности, если ее радиус равен 7 см.
Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².
Ответ: Площадь окружности равна 153,86 см².
Формула нахождения S-площади круга через D-диаметр:
Примеры решения заданий по нахождению S, если известен D:
————————————————————————————————————————-
Задача: Найдите S круга, если его D равен 10 см.
Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².
Ответ: Площадь плоской круглой фигуры равна 78,5 см².
Нахождение S круга, если известна длина окружности:
Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.
Рассмотрим решение на примере задачи:
———————————————————————————————————————-
Задача: Найдите площадь круга, если известна длина окружности L — 12 см.
Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.
Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².
Ответ: Площадь круга равна 11,46 см².
Площадь круга, вписанного в квадрат: формула, примеры решения задач
Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.
Формула нахождения площади круга, вписанного в квадрат:
Примеры решения задач по нахождению площади круга, вписанного в квадрат:
———————————————————————————————————————
Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².
Ответ: Площадь плоской круглой фигуры равна 28,26 см².
————————————————————————————————————————
Задача №2: Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.
Решайте так: Сначала найдем R=a/2=4/2=2 см.
Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².
Ответ: Площадь плоской круглой фигуры равна 12,56 см².
Площадь круга, описанного около квадрата: формула, примеры решения задач
Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.
Формула нахождения S круга, описанного около квадратной фигуры:
Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:
Задача
Площадь круга, вписанного в прямоугольный и равнобедренный треугольник: формула, примеры решения задач
Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
Формула нахождения площади круга, вписанного в равнобедренный треугольник:
Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².
Формула нахождения площади круга, вписанного в прямоугольный треугольник:
Примеры решения заданий:
Задача №1
Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²
Задача №2
Решение:
Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.
Задача №3
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.
Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:
Примеры решения задач:
Вот еще пример решения задачи с использованием формулы Герона.
Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.
Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.
Для решения этой задачи нужно использовать такие формулы:
Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:
Если известна боковая сторона, то можно найти радиус через это значение. Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Примеры решения задач:
Площадь круга, описанного около прямоугольной и равнобедренной трапеции: формула, примеры решения задач
Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:
Примеры решения задач:
Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Ответ: Радиус равен 6.
В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Видео: Математика | Вычисление площадей круга и его частей
Как найти площадь круга? У меня этот вопрос встал очень остро на экзамене по физике в университете, когда я решал одну из задач. Память человека вещь непредсказуемая, сегодня ты помнишь все до мелочей, а завтра это все уже выветрилось из головы. И благо если это была глупость какая, а если нет? Если это день рождения жены или тещи, пароль аккаунта в контакте, или площадь круга. Как это было в моем случае.
Здравствуйте дорогие друзья, меня зовут Валентин Анатольевич, и сегодня мы вычисляем площадь круга 3 способами. Точнее способ будет один, это формула , но вот варианты ее получения будут различны.
Честно говоря, я уже и не помню правильно или нет решил ту задачу, я даже не помню, что это была за задача. Но сам момент того, как выполняя промежуточные расчеты я интегрировал уравнение окружности, чтоб получить казалось бы, простейшую формулу из школьной программы… сильно врезался в память
Итак, первый способ у нас будет от студентов физико-математических факультетов.
Интегрирование.
1. Берем уравнение окружности. Для тех, кто не знает его легко получить из теоремы Пифагора, заменив там катеты на координаты x и y, а за гипотенузу приняв радиус R. Конечно, при условии, что центр окружности будет находится на пересечении координатных осей.
К счастью, это я помнил.
2. Выражаем y.
3. Если вычислить определенный интеграл для значений x от 0 до R, мы получим площадь одной четверти круга.
Соответственно, чтоб получить всю площадь, нам необходимо будет все это безобразие до множить на 4.
4. Давайте выполним замену переменной, и представим x как . Тогда:
.
5. Найдем пределы интегрирования. Для этого необходимо в наше уравнение замены переменной подставить значения x и вычислить чему будет равно t при этих значениях. Получаем промежуток от 0 до .
6. Итак запишем нашу формулу:
7. Сделаем еще кое какие математические преобразования и вычислим определенный интеграл по формуле Ньютона -Лейбница.
Готово!!! В принципе, не так сложно если не впадать в ступор при виде синусов и косинусов, а также уметь интегрировать.
Но вот вопрос. Люди умели находить с большой точностью площадь круга и до интегрального исчисления. Поэтому давайте попробуем обойтись интегралов.
Площадь прямоугольника
Условно, можно сказать, что площадь — это количество квадратиков, со стороной в единицу помещающихся в данной фигуре. К примеру, кухня в хрущевке имеет размеры 2 на 3 метра. Перемножаем длину на ширину и получаем площадь 6 квадратных метров. То есть если у нас имеется 6 квадратных кусков линолеума, со стороной в 1 метр, мы ими полностью без остатка, покроем весь пол.
Прямоугольную кухню легко разбить на квадраты, но что делать если у нас круг? Скажем круглый кусок сыра.
Любой старший прапорщик, обладая не дюжей армейской смекалкой вам скажет, что нужно в таком случае из круга сделать прямоугольник. И он окажется прав. Почему? По тому что старший прапорщик всегда прав.
В общем метод номер два. Метод старших прапорщиков.
Перегруппировка
Делим круг на восемь равных секторов и совмещаем друг с другом.
Отдаленно напоминает прямоугольник? Нет? Отжимаемся восемь раз, и делим еще.
Если секторов будет бесконечно много, то в таком случае, искривления их дуг будут незначительны. А это значит мы получим уже треугольники.
Опять совместим их друг с другом как и в первом случае. И у нас уже идеальный прямоугольник, с шириной равной радиусу , и длиной в половину длины окружности, то есть
.
Перемножаем получаем:
Если внимательно посмотреть на полученную формулу мы увидим, что с её помощью можно найти площадь прямоугольного треугольника с основанием равным длине окружности и высотой равной ее радиусу.
Равенство площадей такого треугольника и круга доказывал Архимед, в своей работе о площадях круга.
Я не буду приводить здесь доказательство этой теоремы, скажу только, что Архимед использовал многоугольники. Один вписанный в окружность, а другой описанный вокруг нее. Площадь круга находилась где-то между площадями этих многоугольников, причем при увеличении сторон, их площади приближались друг к другу, а значит приближались и к площади круга.
Но все же как получить из круга треугольник? Давайте воспользуемся методом неделимых Бонавентуры Кавальери.
Метод неделимых
Представим, что наш круг состоит из бесконечно большого числа окружностей, толщина линий которых стремится к нулю. Если развернуть эти окружности в отрезки и сложить друг на друга стопкой, мы получим треугольник с основанием равным длине большей окружности, то есть и высотой равной радиусу.
Площадь треугольника как известно это половина произведения основания на высоту.
Или в нашем случае .
Те, кто внимательно слушал, наверно помнят, что в теореме Архимеда говорится о прямоугольном треугольнике. Но его довольно легко получить сместив наши отрезки к левому или правому краю. К слову, так легким движением мы докажем еще одну теорему из школьной геометрии. Если знаете какую, пишите в комментариях.
Так же можете написать, как старшие прапорщики находят объем шара, или как бы с этой задачей справился Бонавентура Кавальери.
А я с вами прощаюсь, желаю счастья и до скорых встреч.
В современном машиностроении используется масса элементов и запчастей, которые имеют в своей структуре как внешние окружности, так и внутренние. Самым ярким примером могут служить корпус подшипника, детали моторов, узлы ступицы и многое другое. При их изготовлении применяются не только высокотехнологичные приспособления, но и знания из геометрии, в частности информация об окружностях треугольника. Более детально с подобным знаниями познакомимся ниже….
Какая окружность вписана, а какая описана
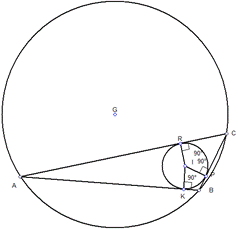
Прежде всего вспомним, что окружностью называется бесконечное множество точек, удаленных на одинаковом расстоянии от центра. Если внутри многоугольника допускается построить окружность, которая с каждой стороной будет иметь только одну общую точку пересечения, то она будет называться вписанной. Описанной окружностью (не круг, это разные понятия) называется такое геометрическое место точек, при котором у построенной фигуры с заданным многоугольником общими точками будут только вершины многоугольника. Ознакомимся с этими двумя понятиями на более наглядном примере (см. рис 1.).
Рисунок 1. Вписанная и описанная окружности треугольника
На изображении построены две фигуры большого и малого диаметров, центры которых находятся G и I. Окружность большего значения называется описанной окр-тью Δ ABC, а малого – наоборот, вписанной в Δ ABC.
Для того чтобы описать вокруг треугольника окр-ть, требуется провести через середину каждой стороны перпендикулярную прямую (т.е. под углом 90°) – это точка пересечения, она играет ключевую роль. Именно она будет представлять собой центр описанной окружности. Перед тем как найти окружность, ее центр в треугольнике, требуется построить для каждого угла биссектрису, после чего выделить точку пересечения прямых. Она в свою очередь будет центром вписанной окр-ти, а ее радиус при любых условиях будет перпендикулярен любой из сторон.
На вопрос:«Какое количество окружностей вписанных может быть для многоугольника с тремя углами?» ответим сразу, что в любой треугольник можно вписать окружность и притом только одну. Потому что существует только одна точка пересечения всех биссектрис и одна точка пересечения перпендикуляров, исходящих из середин сторон.
Свойство окружности, которой принадлежат вершины треугольника
Описанная окружность, которая зависит от длин сторон при основании, имеет свои свойства. Укажем свойства описанной окружности:
- Центр описанной окружности для прямоугольного треугольника находится на середине гипотенузы, у острого – внутри самого треугольника, а для тупоугольного – за ее пределами.
- Диаметр любой описанной окр-сти равен половине отношения стороны и синуса угла, который принадлежит ей, в виде формулы можно представить следующим образом:
- Зная радиус описанной окружности и значения углов, можно найти значение площади, не прибегая к использованию длин сторон, по следующей формуле:
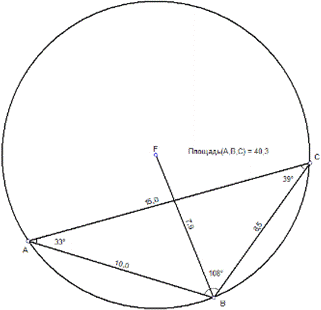
Для того чтобы более наглядно понять принцип описанной окружности, решим простую задачу. Допустим, что дан треугольник Δ ABC, стороны которого равны 10, 15 и 8,5 см. Радиус описанной окружности около треугольника (FB) составляет 7,9 см. Найти значение градусной меры каждого угла и через них площадь треугольника.
Рисунок 2. Поиск радиуса окружности через отношение сторон и синусов углов
Решение: опираясь на ранее указанную теорему синусов, найдем значение синуса каждого угла в отдельности. По условию известно, что сторона АВ равна 10 см. Вычислим значение С:
Используя значения таблицы Брадиса, узнаем, что градусная мера угла С равна 39°. Таким же методом найдем и остальные меры углов:
Откуда узнаем, что CAB = 33°, а ABC = 108°. Теперь, зная значения синусов каждого из углов и радиус, найдем площадь, подставляя найденные значения:
Ответ: площадь треугольника равна 40,31 см², а углы равны соответственно 33°, 108° и 39°.
Важно! Решая задачи подобного плана, будет нелишним всегда иметь таблицы Брадиса либо соответствующее приложение на смартфоне, так как вручную процесс может затянуться на длительное время. Также для большей экономии времени не требуется обязательно строить все три середины перпендикуляра либо три биссектрисы. Любая третья из них всегда будет пересекаться в точке пересечения первых двух. А для ортодоксального построения обычно третью дорисовывают. Может, это неправильно в вопросе алгоритма, но на ЕГЭ или других экзаменах это здорово экономит время.
Исчисление радиуса вписанной окружности
Все точки окружности одинаково удалены от ее центра на одинаковом расстоянии. Длину этого отрезка (от и до) называют радиусом. В зависимости от того, какую окр-ть мы имеем, различают два вида – внутренний и внешний. Каждый из них вычисляется по собственной формуле и имеет прямое отношение к вычислению таких параметров, как:
- площадь,
- градусная мера каждого угла,
- длины сторон и периметр.
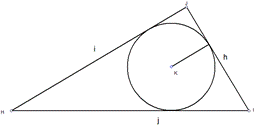
Рисунок 3. Расположение вписанной окружности внутри треугольника
Вычислить длину расстояния от центра до точки соприкосновения с любой из сторон можно такими способами: через стороны, высоты, боковые стороны и углы (для равнобокого треугольника).
Использование полупериметра
Полупериметром называется половина суммы длин всех сторон. Такой способ считается самым популярным и универсальным, потому как независимо от того, какой тип треугольника дан по условию, он подходит для всех. Порядок вычисления имеет следующий вид:
Если дан «правильный»
Одним из малых преимуществ «идеального» треугольника является то, что вписанная и описанная окружности имеют центр в одной точке. Это удобно при построении фигур. Однако в 80% случаев ответ получается «некрасивым». Тут имеется ввиду, что очень редко радиус вписанной окр-ти будет целым натуральным числом, скорее наоборот. Для упрощенного исчисления используется формула радиуса вписанной окружности в треугольник:
Если боковины одинаковой длины
Одним из подтипов задач на гос. экзаменах будет нахождение радиуса вписанной окружности треугольника, две стороны которого равны между собой, а третья нет. В таком случае рекомендуем использовать этот алгоритм, который даст ощутимую экономию времени на поиск диаметра вписанной окр-ти. Радиус вписанной окружности в треугольник с равными «боковыми» вычисляется по формуле:
Более наглядное применение указанных формул продемонстрируем на следующей задаче. Пускай имеем треугольник (Δ HJI), в который вписана окр-ть в точке K. Длина стороны HJ = 16 см, JI = 9,5 см и сторона HI равна 19 см (рисунок 4). Найти радиус вписанной окр-ти, зная стороны.
Рисунок 4. Поиск значения радиуса вписанной окружности
Решение: для нахождения радиуса вписанной окр-ти найдем полупериметр:
Отсюда, зная механизм вычисления, узнаем следующее значение. Для этого понадобятся длины каждой из сторон (дано по условию), а также половину периметра, получается:
Отсюда следует, что искомый радиус равен 3,63 см. Согласно условию, все стороны равны, тогда искомый радиус будет равен:
При условии, если многоугольник равнобокий (например, i = h = 10 см, j = 8 см), диаметр внутренней окр-ти с центром в точке K будет равен:
В условии задачи может даваться треугольник с углом 90°, в таком случае запоминать формулу нет необходимости. Гипотенуза треугольника будет равна диаметру. Более наглядно это выглядит так:
Важно! Если задана задача на поиск внутреннего радиуса, не рекомендуем проводить вычисления через значения синусов и косинусов углов, табличное значение которых точно не известно. В случае, если иначе узнать длину невозможно, не пытайтесь «вытащить» значение из-под корня. В 40% задач полученное значение будет трансцендентным (т.е. бесконечным), а комиссия может не засчитать ответ (даже если он будет правильным) из-за его неточности или неправильной формы подачи. Особое внимание уделите тому, как может видоизменяться формула радиуса описанной окружности треугольника в зависимости от предложенных данных. Такие «заготовки» позволяют заранее «видеть» сценарий решения задачи и выбрать наиболее экономное решение.
Радиус внутренней окружности и площадь
Для того чтобы вычислить площадь треугольника, вписанного в окружность, используют лишь радиус и длины сторон многоугольника:
Если в условии задачи напрямую не дано значение радиуса, а только площадь, то указанная формула площади трансформируется в следующую:
Рассмотрим действие последней формулы на более конкретном примере. Предположим, что дан треугольник, в который вписана окр-ть. Площадь окр-ти составляет 4π, а стороны равны соответственно 4, 5 и 6 см. Вычислим площадь заданного многоугольника при помощи вычисления полупериметра.
Используя вышеуказанный алгоритм, вычислим площадь треугольника через радиус вписанной окружности:
В силу того, что в любой треугольник можно вписать окружность, число вариаций нахождения площади значительно увеличивается. Т.е. поиск площади треугольника, включает в себя обязательное знание длины каждой стороны, а также значение радиуса.
Треугольник, вписанный в окружность геометрия 7 класс
Прямоугольные треугольники, вписанные в окружность
Вывод
Из указанных формул можно убедиться, что сложность любой задачи с использованием вписанной и описанной окружностей заключается только в дополнительных действия по поиску требуемых значений. Задачи подобного типа требуют только досконально понимания сути формул, а также рациональности их применения. Из практики решения отметим, что в будущем центр описанной окружности будет фигурировать и в дальнейших темах геометрии, поэтому запускать ее не следует. В противном случае решение может затянуться с использованием лишних ходов и логических выводов.





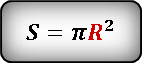
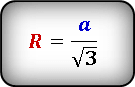
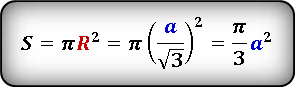
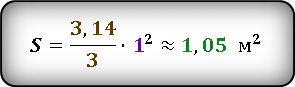
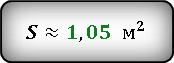
























![Rendered by QuickLaTeX.com [frac{1}{4}S=intlimits_0^R sqrt{R^2-x^2},dx]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-7479e3008654e9c55630ae7d0c7ce5ec_l3.png)
![Rendered by QuickLaTeX.com [S=4intlimits_0^R sqrt{R^2-x^2},dx]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-2b4a6b16249e47f6a9dfc672448a89a6_l3.png)
![Rendered by QuickLaTeX.com [S=4intlimits_0^{frac{pi}{2}} sqrt{R^2-R^2sin^2t},R cos tdt]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-704a72c6e8263e0685fa3df05b5b1ac2_l3.png)
![Rendered by QuickLaTeX.com [S=4R^2intlimits_0^{frac{pi}{2}} cos^2t dt = 4R^2intlimits_0^{frac{pi}{2}} frac{1}{2}}(1+ 2cos{2t}) dt = 2R^2(intlimits_0^{frac{pi}{2}} dt + intlimits_0^{frac{pi}{2}} cos 2t dt) =]](https://newtonov.ru/wp-content/ql-cache/quicklatex.com-28adf484dcf6d0491f78ba9e93b79cf4_l3.png)