Как найти площадь окружности в питоне - Исправление недочетов и поиск решений вместе с Examum.ru

В этом уроке мы покажем, как пользователь может вычислить площадь круга, используя Python с заданным радиусом данного круга.

Чтобы понять формат ввода-вывода кода, пользователь должен обратить внимание на следующее:

Входные данные кода состоят из целого числа «R», которое представляет радиус круга.
На выходе кода будет напечатана область круга.

Алгоритм вычисления площади

Ниже приведены шаги, которые мы будем использовать для вычисления площади данного круга:

Шаг 1. Мы должны передать ввод с помощью функции input(). Вход будет соответствовать радиусу данного круга.
Шаг 2: Площадь круга будет рассчитана по формуле: Площадь = πR2.

Площадь круга = π * R * R

Где π(PI) = 3.14

R = радиус круга

D или(2R) = Диаметр круга, (R + R).

Шаг 3: Распечатаем вывод кода, то есть площадь данного круга.

Метод 1. Найти площадь данного круга с помощью математического модуля.

 
import math as M 
Radius = float(input("Please enter the radius of the given circle: ")) 
area_of_the_circle = M.pi* Radius * Radius 
print(" The area of the given circle is: ", area_of_the_circle)

Выход:

Please enter the radius of the given circle:  3 
 The area of the given circle is:  28.274333882308138

Метод 2. Вычислить площадь данного круга с помощью π.

 
π = 3.14 
Radius = float(input("Please enter the radius of the given circle: ")) 
area_of_the_circle = π * Radius * Radius 
print(" The area of the given circle is: ", area_of_the_circle)

Выход:

Please enter the radius of the given circle:  3 
 The area of the given circle is:  28.259999999999998

Метод 3. Вычислить площадь данного круга с помощью функции.

 
import math 
 
def area_of_the_circle(Radius):  
    area = Radius** 2 * math.pi 
    return area 
 
Radius = float(input("Please enter the radius of the given circle: ")) 
print(" The area of the given circle is: ", area_of_the_circle(Radius))

Выход:

Please enter the radius of the given circle:  3 
 The area of the given circle is:  28.274333882308138

Заключение

В этом уроке мы показали три метода вычисления площади данного круга. Чтобы ее вычислить, пользователь должен знать радиус или диаметр данного круга. Из трех методов первый – самый простой и точный.

Изучаю Python вместе с вами, читаю, собираю и записываю информацию опытных программистов.

Источник

Перейти к содержанию

На чтение 2 мин Просмотров 1.2к. Опубликовано 14.03.2023

Содержание

Введение
Импорт модуля math
Находим длину окружности
Находим площадь круга
Заключение

Введение

В статье напишем скрипт на языке программирования Python для нахождения длины окружности и площади круга.

Импорт модуля math

Для нахождения длины окружности, и площади круга понадобится использовать число Пи.

Импортируем модуль math, т.к. оно присутствует там:

Находим длину окружности

Формула нахождения длины окружности:

Дадим пользователю возможность ввести радиус:

import math

r = float(input('Введите радиус: '))

Произведём расчёты по формуле:

import math

r = float(input('Введите радиус: '))
p = 2 * math.pi * r

print(f'Длина = {p:.2f}')

Находим площадь круга

Формула нахождения площади круга:

Добавим к ранее написанному коду вычисление площади круга по формуле и выведем результат:

import math

r = float(input('Введите радиус: '))

p = 2 * math.pi * r
s = math.pi * math.pow(r, 2)

print(f'Длина = {p:.2f}')
print(f'Площадь = {s:.2f}')

# Введите радиус: 10
# Длина = 62.83
# Площадь = 314.16

Заключение

В ходе статьи мы с Вами написали скрипт для нахождения длины окружности и площади круга на языке программирования Python. Надеюсь Вам понравилась статья, желаю удачи и успехов! 🙂

Admin

Источник

In this tutorial, we will learn how to find the area of a circle using the Python programing language. Previously, we saw how to find the area of a square, we will follow a similar approach and use the formula for calculating the area of a circle.

Formula:

Our program should take input as follows and display area as output.

For a circle with a radius of 7 cm, the area of a circle is 154cm

Input— Radius: 7

Output— Area: 154

Look at the algorithm below to understand the working.

Algorithm

Step 1— Define a function area_of_circle()

Step 2— Set pi as constant and initialize to 3.147

Step 3— Declare variable area to calculate and store area

Step 4— Return area

Step 5- Take input of radius from the user

Step 6— Pass radius in the function

Step 7— Print the result

Python Program

Look at the program to understand the implementation of the above-mentioned approach.

def area_of_circle(r):
    pi=3.147
    area= pi*r*r
    return area

radius=float(input("Enter Radius: "))
print("Area: ",area_of_circle(radius))

Enter Radius: 3.2
Area: 32.22528

To calculate area, we can also use the pow() function which is a function in the math class of the Python library.

The pow(x,y) returns the value of x raised to the power y.

In place of pi*r*r in #line 8 of the code, we can also write pi*pow(r,2) to calculate area.

To know about Python math library functions in detail check out this article.

Conclusion

So far, we have learned how to define a function to calculate the area of a circle where the radius is given by the user in Python. In the function body, we have set pi as a constant value and put it in the formula along with the radius to calculate the area. Finally, the area was returned by the function and displayed using the print() function.

Источник

Описание задачи

Программа получает на вход радиус и вычисляет площадь круга и длину окружности, используя классы.

Решение задачи

Получаем от пользователя величину радиуса.
Создаем класс и инициализируем его полученным значением.
Создаем метод area, который вычисляет площадь круга, и метод perimeter для вычисления длины окружности.
Создаем объект этого класса.
При помощи созданного объекта вызываем оба его метода для вычисления площади круга и длины окружности.
Выводим полученный результат на экран.
Конец.

Исходный код

Ниже дан исходный код, который осуществляет нахождение площади круга и длины окружности с использованием классов. Результаты работы программы также даны ниже.

import math

class circle():
    def __init__(self, radius):
        self.radius = radius
    def area(self):
        return math.pi * (self.radius**2)
    def perimeter(self):
        return 2 * math.pi * self.radius
 
r = int(input("Введите радиус круга: "))
obj = circle(r)
print("Площадь круга:", round(obj.area(), 2))
print("Длина окружности:", round(obj.perimeter(), 2))

Объяснение работы программы

Пользователь вводит значение радиуса круга, которое сохраняется в переменной r.
Создаем класс под названием circle и при помощи конструктора __init__() инициализируем его значения.
Метод area() возвращает math.pi * (self.radius**2), что является площадью круга.
Еще один метод perimeter возвращает 2 * math.pi * self.radius, что является длиной окружности.
Создаем объект этого класса со значениями, полученными от пользователя.
С помощью методов area() и perimeter() , вызываемых прямо на экземпляре класса, вычисляем площадь круга и длину окружности.
Выводим результаты на экран.

Результаты работы программы

Пример 1:
Введите радиус круга: 5
Площадь круга: 78.54
Длина окружности: 31.42	
 
Пример 2:
Введите радиус круга: 10
Площадь круга: 314.16
Длина окружности: 62.83

Источник

Перейти к содержанию

На чтение 1 мин Просмотров 1.4к. Опубликовано 18 июня, 2022 Обновлено 18 июня, 2022

По введенному с клавиатуры радиусу вычислить длину соответствующей окружности и площадь круга. Формулы:

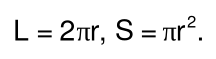
import math

r = input("Radius = ")
r = float(r)

ln = 2 * math.pi * r
area = math.pi * math.pow(r, 2)

print('Length = %.2f' % ln)
print('Area = %.2f' % area)

Пример выполнения:

Radius = 3.8
Length = 23.88
Area = 45.36

Данную задачу можно решить без использования «константы» и функции модуля math. Так в
самом Питоне есть оператор возведения в степень – два знака звездочки **. Вместо «константы»
math.pi можно просто записать число 3.14. Однако при этом пострадает точность вычисления.

r = input("Radius = ")
r = float(r)

pi = 3.14
ln = 2 * pi * r
area = pi * r**2

print("Length = %.2f" % ln)
print("Area = %.2f" % area)

Пример выполнения:

Radius = 3.8
Length = 23.86
Area = 45.34

Поскольку значение 3.14 играет роль константы и используется несколько раз, мы можем ввести
свою «константу».

pi = 3.14
ln = 2 * pi * r
area = pi * r ** 2

Обратим внимание, в языке Python нет настоящих констант – переменных, навсегда
привязанных к одному значению.

( 3 оценки, среднее 3 из 5 )

Источник