Как найти площадь октаэдра формула

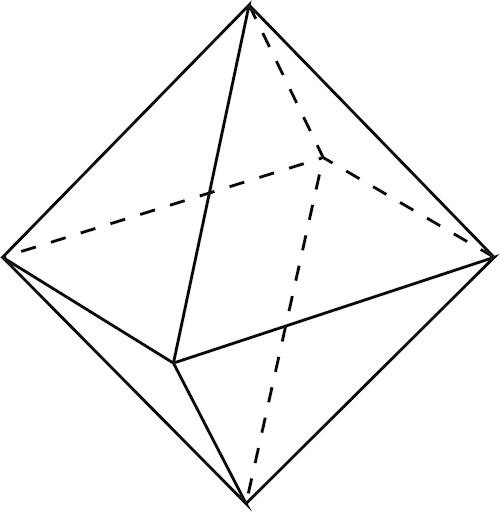
Октаэдр – тоже один из правильных многогранников, как и тетраэдр (у правильного многогранника все грани – одинаковые равносторонние фигуры). Как ясно из названия, у октаэдра 8 граней – для того чтобы получить такой многогранник, нужно приложить две четырехугольные пирамиды основаниями друг к другу. У октаэдра не будет основания ввиду его остроугольной формы с двух сторон, поэтому площадь полной поверхности октаэдра и будет единственной его площадью, состоящей из восьми равносторонних треугольников:

Октаэдр и площадь полной его поверхности: описание, формулы, примеры

Содержание:

Существует несколько способов определить площадь поверхности октаэдра. Он представляет собой один из пяти правильных многоугольников или так называемых Платоновых тел. Имеет восемь одинаковых граней (поверхностей) в виде равносторонних треугольников, к каждой из его вершин прилагается по четыре грани. Рассмотрим, что собой представляет тело, где встречается в природе, как вычисляется его площадь и объём.

Что такое октаэдр

Свойства октаэдра

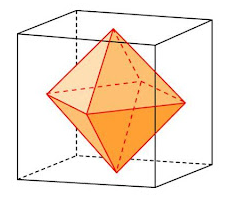
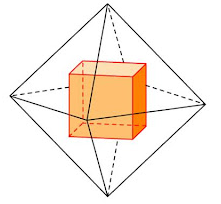
1. В тело вписывается куб, вершины которого находятся в центрах граней куба.

1. Симметрия куба и вписанного (описанного) октаэдра совпадают.

1. Двойственен кубу.

1. Является полным усечением тетраэдра.

1. Имеет равные ребра и диагонали.

1. Состоит из равносторонних треугольников.

1. Диагонали тела взаимоперпендикулярны, в точке пересечения делятся на равные отрезки.

1. Октаэдр симметричен, причём 3 оси пролегают через противоположные вершины, 6 – через центры ребер.

1. Центр симметрии тела расположен в точке пересечения диагоналей.

1. Ребра равны по длине, поверхности – по площади.

Математические характеристики тела

Как вычислить площадь поверхности октаэдра

Площадь октаэдра равна сумме площадей составляющих его треугольников:

Здесь S_треуг – площадь треугольника.

После подстановки значения получится требуемый результат.

Если известна длина ребра, придётся вычислить площадь треугольников.

Подставляем значение в первое выражение:

Упрощаем: после сокращения дроби на четыре получается формула площади поверхности октаэдра:

2. S = 8 * S_треуг = 2 sqrt <3>a^2.

Существует ещё один способ проведения вычислений. Он менее точный чем предыдущие, однако позволяет обойтись без калькулятора. При приблизительном подсчёте 2 sqrt <3>равняется 3,464 или 3,46.

Здесь a – длина стороны треугольника (равны).

Для примера, имеется фигура октаэдр с длиной стороны 5 см.

S=2sqrt <3>a^2=2*sqrt <3>*5^2=2*sqrt <3>*25=50sqrt <3>approx 86,6 см.

Как вычислить объём правильного октаэдра

Объём показывает размер внутреннего пространства геометрического тела. Объем правильного октаэдра вычисляется, если знаете длину ребра геометрического тела, по формуле:

После проведения приблизительных расчётов frac<sqrt 2> <3>approx 0,47 формула принимает следующий вид :

Рассчитаем двумя методами на примере правильного многоугольника с гранью, равной 5 см:

V= 0,47 * a^3 = 0,47*125 approx 58,93

Значения совпали, во втором случае нужно выполнять гораздо меньше операций. Подходит он только, если не требуется исключительная точность – при округлении до 4-5 знаков после запятой точность снизится.

Развёртка

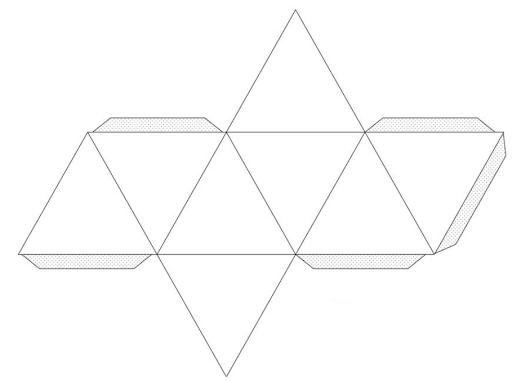
Октаэдр, как большинство гомерических тел, имеет развёртку поверхности – это плоская фигура, полученная путём совмещения поверхности модели с одной плоскостью без пересечения либо наложения граней друг на друга.

Рисунок развёртки октаэдра.

В природе насчитывается 11 разновидностей развёртки октаэдра, позволяющих создать его модель из бумаги или картона. Наиболее распространённая выглядит как восемь одинаковых треугольников. Шесть из них размещено в ряд, к третьему и четвёртому основаниям прилегает ещё по одному, их вершины направлены в противоположные стороны.

Октаэдр.

Октаэдр — один из 5-ти выпуклых правильных многогранников — Платоновых тел.

У октаэдра 8 треугольных граней, 12 рёбер, 6 вершин, к каждой его вершине сходятся 4 ребра.

На примере октаэдра легко проверить формулу Эйлера 6в+8г-12р=2. В каждой из вершин октаэдра сходятся 4 треугольника, т.о., сумма плоских углов у вершины октаэдра равна 240°. Из понятия правильного многогранника делаем вывод, что каждое ребра октаэдра имеет одинаковую длину, а грань — одинаковую площадь.

Обозначим длину ребра октаэдра как а, значит площадь полной поверхности октаэдра (S) и объём октаэдра (V) найдем из таких формул:

Радиус описанной сферы около октаэдра:

Радиус вписанной сферы около октаэдра:

Сумма длин всех ребер равна 24а.

Двугранный угол: α=2ϕ≈109,47°, где .

Свойства октаэдра.

Октаэдр легко вписывается в тетраэдр, при этом 4 из 8-ми граней октаэдра совместятся с 4-мя гранями тетраэдра, каждая из 6-ти вершин октаэдра совместится с центрами 6-ти ребер тетраэдра.

Октаэдр легко вписывается в куб (гексаэдр), при этом каждая из 6-ти вершин октаэдра совместится с центрами 6-ти граней куба.

В октаэдр легко вписать куб, при этом каждая из 8-ми вершин куба будут располагаться в центрах 8-ми граней октаэдра.

У правильного октаэдра есть симметрия O_h, которая совпадает с симметрией куба.

Развёртка октаэдра.

Симметрия октаэдра.

3 из девяти осей симметрии октаэдра проходят сквозь противолежащие

вершины, 6 — квозь середины ребер.

Центр симметрии октаэдра — точка пересечения осей симметрии октаэдра.

3 из девяти плоскостей симметрии тетраэдра проходят сквозь все 4 вершины октаэдра, которые лежат в одной плоскости.

6 плоскостей симметрии проходят через 2 вершины, которые не принадлежат одной грани, и середины противолежащих ребер.

Октаэдр

Древние греки дали многограннику имя по числу граней. «Окто» означает восемь, «хедра» — означает грань (октаэдр – восьмигранник).

Поэтому на вопрос — «что такое октаэдр?», можно дать следующее определение: » Октаэдр это геометрическое тело из восьми граней, каждая их которых — правильный треугольник «.

Многогранник относится к правильным многогранникам и является одним из пяти Платоновых тел .

Октаэдр имеет следующие характеристики:

• Тип грани – правильный треугольник;
• Число сторон у грани – 3;
• Общее число граней – 8;
• Число рёбер, примыкающих к вершине – 4;
• Общее число вершин – 6;
• Общее число рёбер – 12;

Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240°.

Октаэдр имеет центр симметрии — центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.

Математические характеристики октаэдра

Октаэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.

Радиус описанной сферы октаэдра определяется по формуле:

, где a — длина стороны.

Сфера может быть вписана внутрь октаэдра.

Радиус вписанной сферы октаэдра определяется по формуле:

Площадь поверхности октаэдра

Для наглядности, площадь поверхности октаэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон октаэдра (это площадь правильного треугольника) умноженной на 8. Либо воспользоваться формулой:

Объем октаэдра определяется по следующей формуле:

Октаэдр можно представить в виде двух правильных пирамид с четырехугольным основанием, соединенных друг с другом через это основание.

Вариант развертки

Октаэдр можно изготовить самостоятельно. Бумага или картон самый подходящий вариант. Для сборки потребуется бумажная развёртка — единая деталь с линиями сгибов.

Древнегреческий философ Платон ассоциировал октаэдр с «земным» элементом воздух, поэтому для построения модели этого правильного многогранника мы выбрали серый цвет.

Заметим, что это не единственный вариант развертки.

Для построения модели Вы можете скачать развертку в формате pdf и распечатать на листе формата А4:
— если Вы предполагаете распечатать на цветном принтере — цветная развертка
— если Вы предполагаете использовать для сборки цветной картон — развертка

Классический вариант раскраски предполагает окраску октаэдра четырьмя различными цветами, причем таким образом, что каждая грань имеет свой цвет отличный от соседней и только противоположные не соприкасающиеся друг с другом грани окрашиваются в одинаковые цвета.

Вариант окраски представлен на рисунке. Вы можете скачать развертку с соответствующей раскраской граней.

Видео. Октаэдр из набора «Волшебные грани»

Вы можете изготовить модель октаэдра воспользовавшись деталями для сборки из набора «Волшебные грани».

Сборка многогранника из набора:

Подробная сборка от Алексея Жигулева (youtube-канал PRO)

Подробная сборка от Алексея Жигулева (youtube-канал PRO)

вращение готового многогранника:

Видео. Вращение правильных многогранников

источники:

http://www.calc.ru/Oktaedr.html

http://mnogogranniki.ru/oktaedr.html

Правильные многогранники

Существует всего пять правильных многогранников:

• Тетраэдр
• Куб (Гексаэдр)
• Октаэдр
• Икосаэдр
• Додекаэдр

Если какое-то из этих названий звучит для тебя как древний эльфийский язык, обязательно прочитай эту статью!

Давай посмотрим, как они выглядят, и разберем основные формулы – площади поверхности, объема, радиусов вписанной и описанной сферы.

А также решим задачу №8.

О том, как рисовать пространственные фигуры на плоскости, можно прочитать в нашей статье: «Изображение пространственных фигур. Визуальный гид».

Поехали!

Правильные многогранники — подробнее

Многогранник называется правильным, если:

• он выпуклый;
• все его грани являются правильными многоугольниками;
• в каждой его вершине сходится одинаковое число его ребер.

Пять правильных многогранников

Тетраэдр

Тетраэдр состоит из четырёх равносторонних треугольников.

Фигура имеет 4 грани, 4 вершины и 6 ребер(a).

Площадь поверхности тетраэдра:

( displaystyle S={{a}^{2}}sqrt{3})

Объем тетраэдра:

( displaystyle V=frac{{{a}^{3}}}{12}sqrt{2})

Радиус описанной вокруг тетраэдра сферы:

( displaystyle R=frac{a}{4}sqrt{6})

Радиус вписанной в тетраэдр сферы:

( displaystyle R=frac{a}{12}sqrt{6})

Куб (Гексаэдр)

Куб состоит из шести квадратов.

 Фигура имеет 6 граней, 8 вершин и 12 ребер (a).

Площадь поверхности куба:

( displaystyle S=6{{a}^{2}})

Объем куба:

( displaystyle V={{a}^{3}})

Радиус описанной вокруг куба сферы:

( displaystyle R=frac{a}{2}sqrt{3})

Радиус вписанной в куб сферы:

( displaystyle r=frac{a}{2})

Октаэдр

Октаэдр составлен из восьми равносторонних треугольников.

Фигура имеет 8 граней, 6 вершин и 12 ребер (a).

Площадь поверхности октаэдра:

( displaystyle S=2{{a}^{2}}sqrt{3})

Объем октаэдра:

( displaystyle V=frac{{{a}^{3}}}{3}sqrt{2})

Радиус описанной вокруг октаэдра сферы:

( displaystyle R=frac{a}{2}sqrt{2})

Радиус вписанной в октаэдр сферы:

( displaystyle r=frac{a}{6}sqrt{6})

Икосаэдр

Икосаэдр составлен из двадцати равносторонних треугольников.

Фигура имеет 20 граней, 12 вершин и 30 ребер (a).

Площадь поверхности икосаэдра:

( displaystyle S=5{{a}^{2}}sqrt{3})

Объем икосаэдра:

( displaystyle V=frac{5{{a}^{3}}}{12}left( 3+sqrt{5} right))

Радиус описанной вокруг икосаэдра сферы:

( displaystyle R=frac{a}{4}sqrt{2left( 5+sqrt{5} right)})

Радиус вписанной в икосаэдр сферы:

( displaystyle r=frac{a}{4sqrt{3}}left( 3+sqrt{5} right))

Додекаэдр

Додекаэдр составлен из двенадцати равносторонних пятиугольников.

Фигура имеет 12 граней, 20 вершин и 30 ребер (a).

Площадь поверхности додекаэдра:

( displaystyle S=3{{a}^{2}}sqrt{5left( 5+2sqrt{5} right)})

Объем додекаэдра:

( displaystyle V=frac{{{a}^{3}}}{4}left( 15+7sqrt{5} right))

Радиус описанной вокруг додекаэдра сферы:

( displaystyle R=frac{a}{4}left( 1+sqrt{5} right)sqrt{3})

Радиус вписанной в додекаэдр сферы:

( displaystyle r=frac{a}{4}sqrt{10+frac{22}{sqrt{5}}})

Решение задачи №8 на тему «Правильные многогранники»

Задача:

В кубе ( displaystyle ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}) с ребром ( displaystyle sqrt{12}) найдите ( displaystyle A{{C}_{1}}).

Решение:

( displaystyle d=asqrt{3}),

где ( displaystyle d) – диагональ куба,( displaystyle a) – сторона куба.( displaystyle A{{C}_{1}}) – это и есть диагональ куба.

Тогда ( displaystyle A{{C}_{1}}=asqrt{3}=sqrt{12}cdot sqrt{3}=sqrt{36}=6).

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук — ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 — WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org — email для записи

• тысячи учеников, поступивших в лучшие ВУЗы страны
• автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
• закончил МФТИ, преподавал на малом физтехе;
• репетиторский стаж — c 2003 года;
• в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
• отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».

From Wikipedia, the free encyclopedia

Regular octahedron
(Click here for rotating model)
Type	Platonic solid
Elements	F = 8, E = 12 V = 6 (χ = 2)
Faces by sides	8{3}
Conway notation	O aT
Schläfli symbols	{3,4}
r{3,3} or {}+{}+{}=3{}
Face configuration	V4.4.4
Wythoff symbol	4 | 2 3
Coxeter diagram
Symmetry	Oh, BC3, [4,3], (*432)
Rotation group	O, [4,3]+, (432)
References	U05, C17, W2
Properties	regular, convexdeltahedron, Hanner polytope
Dihedral angle	109.47122° = arccos(−1⁄3)
3.3.3.3 (Vertex figure)	Cube (dual polyhedron)
Net

In geometry, an octahedron (PL octahedra or octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.

A regular octahedron is the dual polyhedron of a cube. It is a rectified tetrahedron. It is a square bipyramid in any of three orthogonal orientations. It is also a triangular antiprism in any of four orientations.

An octahedron is the three-dimensional case of the more general concept of a cross polytope.

A regular octahedron is a 3-ball in the Manhattan (ℓ₁) metric.

Regular octahedron[edit]

Dimensions[edit]

If the edge length of a regular octahedron is a, the radius of a circumscribed sphere (one that touches the octahedron at all vertices) is

and the radius of an inscribed sphere (tangent to each of the octahedron’s faces) is

while the midradius, which touches the middle of each edge, is

Orthogonal projections[edit]

The octahedron has four special orthogonal projections, centered, on an edge, vertex, face, and normal to a face. The second and third correspond to the B₂ and A₂ Coxeter planes.

Orthogonal projections

Centered by	Edge	Face Normal	Vertex	Face
Image
Projective symmetry	[2]	[2]	[4]	[6]

Spherical tiling[edit]

The octahedron can also be represented as a spherical tiling, and projected onto the plane via a stereographic projection. This projection is conformal, preserving angles but not areas or lengths. Straight lines on the sphere are projected as circular arcs on the plane.

Orthographic projection	Stereographic projection

Cartesian coordinates[edit]

An octahedron with edge length √2 can be placed with its center at the origin and its vertices on the coordinate axes; the Cartesian coordinates of the vertices are then

( ±1, 0, 0 );

( 0, ±1, 0 );

( 0, 0, ±1 ).

In an x–y–z Cartesian coordinate system, the octahedron with center coordinates (a, b, c) and radius r is the set of all points (x, y, z) such that

Area and volume[edit]

The surface area A and the volume V of a regular octahedron of edge length a are:

Thus the volume is four times that of a regular tetrahedron with the same edge length, while the surface area is twice (because we have 8 rather than 4 triangles).

If an octahedron has been stretched so that it obeys the equation

the formulas for the surface area and volume expand to become

Additionally the inertia tensor of the stretched octahedron is

These reduce to the equations for the regular octahedron when

Geometric relations[edit]

Using the standard nomenclature for Johnson solids, an octahedron would be called a square bipyramid.

Dual[edit]

The octahedron is the dual polyhedron of the cube.

If an octahedron of edge length is inscribed in a cube, then the length of an edge of the cube .

Stellation[edit]

The interior of the compound of two dual tetrahedra is an octahedron, and this compound, called the stella octangula, is its first and only stellation. Correspondingly, a regular octahedron is the result of cutting off from a regular tetrahedron, four regular tetrahedra of half the linear size (i.e. rectifying the tetrahedron). The vertices of the octahedron lie at the midpoints of the edges of the tetrahedron, and in this sense it relates to the tetrahedron in the same way that the cuboctahedron and icosidodecahedron relate to the other Platonic solids.

Snub octahedron[edit]

One can also divide the edges of an octahedron in the ratio of the golden mean to define the vertices of an icosahedron. This is done by first placing vectors along the octahedron’s edges such that each face is bounded by a cycle, then similarly partitioning each edge into the golden mean along the direction of its vector. There are five octahedra that define any given icosahedron in this fashion, and together they define a regular compound. An icosahedron produced this way is called a snub octahedron.

Tessellations[edit]

Octahedra and tetrahedra can be alternated to form a vertex, edge, and face-uniform tessellation of space. This and the regular tessellation of cubes are the only such uniform honeycombs in 3-dimensional space.

Characteristic orthoscheme[edit]

Like all regular convex polytopes, the octahedron can be dissected into an integral number of disjoint orthoschemes, all of the same shape characteristic of the polytope. A polytope’s characteristic orthoscheme is a fundamental property because the polytope is generated by reflections in the facets of its orthoscheme. The orthoscheme occurs in two chiral forms which are mirror images of each other. The characteristic orthoscheme of a regular polyhedron is a quadrirectangular irregular tetrahedron.

The faces of the octahedron’s characteristic tetrahedron lie in the octahedron’s mirror planes of symmetry. The octahedron is unique among the Platonic solids in having an even number of faces meeting at each vertex. Consequently, it is the only member of that group to possess, among its mirror planes, some that do not pass through any of its faces. The octahedron’s symmetry group is denoted B₃. The octahedron and its dual polytope, the cube, have the same symmetry group but different characteristic tetrahedra.

The characteristic tetrahedron of the regular octahedron can be found by a canonical dissection^[1] of the regular octahedron which subdivides it into 48 of these characteristic orthoschemes surrounding the octahedron’s center. Three left-handed orthoschemes and three right-handed orthoschemes meet in each of the octahedron’s eight faces, the six orthoschemes collectively forming a trirectangular tetrahedron: a triangular pyramid with the octahedron face as its equilateral base, and its cube-cornered apex at the center of the octahedron.^[2]

Characteristics of the regular octahedron[3]
	edge	arc	dihedral
𝒍		90°		109°28′
𝟀		54°44′8″		90°
𝝓		45°		60°
𝟁		35°15′52″		45°
		35°15′52″

If the octahedron has edge length 𝒍 = 2, its characteristic tetrahedron’s six edges have lengths , , (the exterior right triangle face, the characteristic triangle 𝟀, 𝝓, 𝟁 of the octahedron), plus , , (edges that are the characteristic radii of the octahedron). The 3-edge path along orthogonal edges of the orthoscheme is , , , first from an octahedron vertex to an octahedron edge center, then turning 90° to an octahedron face center, then turning 90° to the octahedron center. The orthoscheme has four dissimilar right triangle faces. The exterior face is a 90-60-30 triangle which is one-sixth of an octahedron face. The three faces interior to the octahedron are: a 45-90-45 triangle with edges , , , a right triangle with edges , , , and a right triangle with edges , , .

Topology[edit]

The octahedron is 4-connected, meaning that it takes the removal of four vertices to disconnect the remaining vertices. It is one of only four 4-connected simplicial well-covered polyhedra, meaning that all of the maximal independent sets of its vertices have the same size. The other three polyhedra with this property are the pentagonal dipyramid, the snub disphenoid, and an irregular polyhedron with 12 vertices and 20 triangular faces.^[4]

Nets[edit]

The regular octahedron has eleven arrangements of nets.

Faceting[edit]

The uniform tetrahemihexahedron is a tetrahedral symmetry faceting of the regular octahedron, sharing edge and vertex arrangement. It has four of the triangular faces, and 3 central squares.

Uniform colorings and symmetry[edit]

There are 3 uniform colorings of the octahedron, named by the triangular face colors going around each vertex: 1212, 1112, 1111.

The octahedron’s symmetry group is O_h, of order 48, the three dimensional hyperoctahedral group. This group’s subgroups include D_3d (order 12), the symmetry group of a triangular antiprism; D_4h (order 16), the symmetry group of a square bipyramid; and T_d (order 24), the symmetry group of a rectified tetrahedron. These symmetries can be emphasized by different colorings of the faces.

Name	Octahedron	Rectified tetrahedron (Tetratetrahedron)	Triangular antiprism	Square bipyramid	Rhombic fusil
Image (Face coloring)	(1111)	(1212)	(1112)	(1111)	(1111)
Coxeter diagram		=
Schläfli symbol	{3,4}	r{3,3}	s{2,6} sr{2,3}	ft{2,4} { } + {4}	ftr{2,2} { } + { } + { }
Wythoff symbol	4 | 3 2	2 | 4 3	2 | 6 2 | 2 3 2
Symmetry	Oh, [4,3], (*432)	Td, [3,3], (*332)	D3d, [2+,6], (2*3) D3, [2,3]+, (322)	D4h, [2,4], (*422)	D2h, [2,2], (*222)
Order	48	24	12 6	16	8

Irregular octahedra[edit]

The following polyhedra are combinatorially equivalent to the regular polyhedron. They all have six vertices, eight triangular faces, and twelve edges that correspond one-for-one with the features of a regular octahedron.

• Triangular antiprisms: Two faces are equilateral, lie on parallel planes, and have a common axis of symmetry. The other six triangles are isosceles.
• Tetragonal bipyramids, in which at least one of the equatorial quadrilaterals lies on a plane. The regular octahedron is a special case in which all three quadrilaterals are planar squares.
• Schönhardt polyhedron, a non-convex polyhedron that cannot be partitioned into tetrahedra without introducing new vertices.
• Bricard octahedron, a non-convex self-crossing flexible polyhedron

More generally, an octahedron can be any polyhedron with eight faces. The regular octahedron has 6 vertices and 12 edges, the minimum for an octahedron; irregular octahedra may have as many as 12 vertices and 18 edges.^[5]
There are 257 topologically distinct convex octahedra, excluding mirror images. More specifically there are 2, 11, 42, 74, 76, 38, 14 for octahedra with 6 to 12 vertices respectively.^[6][7] (Two polyhedra are «topologically distinct» if they have intrinsically different arrangements of faces and vertices, such that it is impossible to distort one into the other simply by changing the lengths of edges or the angles between edges or faces.)

Some better known irregular octahedra include the following:

• Hexagonal prism: Two faces are parallel regular hexagons; six squares link corresponding pairs of hexagon edges.
• Heptagonal pyramid: One face is a heptagon (usually regular), and the remaining seven faces are triangles (usually isosceles). It is not possible for all triangular faces to be equilateral.
• Truncated tetrahedron: The four faces from the tetrahedron are truncated to become regular hexagons, and there are four more equilateral triangle faces where each tetrahedron vertex was truncated.
• Tetragonal trapezohedron: The eight faces are congruent kites.
• Octagonal hosohedron: degenerate in Euclidean space, but can be realized spherically.

Octahedra in the physical world[edit]

Octahedra in nature[edit]

• Natural crystals of diamond, alum or fluorite are commonly octahedral, as the space-filling tetrahedral-octahedral honeycomb.
• The plates of kamacite alloy in octahedrite meteorites are arranged paralleling the eight faces of an octahedron.
• Many metal ions coordinate six ligands in an octahedral or distorted octahedral configuration.
• Widmanstätten patterns in nickel-iron crystals

Octahedra in art and culture[edit]

• Especially in roleplaying games, this solid is known as a «d8», one of the more common polyhedral dice.
• If each edge of an octahedron is replaced by a one-ohm resistor, the resistance between opposite vertices is 1/2 ohm, and that between adjacent vertices 5/12 ohm.^[8]
• Six musical notes can be arranged on the vertices of an octahedron in such a way that each edge represents a consonant dyad and each face represents a consonant triad; see hexany.

Tetrahedral octet truss[edit]

A space frame of alternating tetrahedra and half-octahedra derived from the Tetrahedral-octahedral honeycomb was invented by Buckminster Fuller in the 1950s. It is commonly regarded as the strongest building structure for resisting cantilever stresses.

[edit]

A regular octahedron can be augmented into a tetrahedron by adding 4 tetrahedra on alternated faces. Adding tetrahedra to all 8 faces creates the stellated octahedron.

tetrahedron	stellated octahedron

The octahedron is one of a family of uniform polyhedra related to the cube.

Uniform octahedral polyhedra
Symmetry: [4,3], (*432)	[4,3]+ (432)	[1+,4,3] = [3,3] (*332)	[3+,4] (3*2)
{4,3}	t{4,3}	r{4,3} r{31,1}	t{3,4} t{31,1}	{3,4} {31,1}	rr{4,3} s2{3,4}	tr{4,3}	sr{4,3}	h{4,3} {3,3}	h2{4,3} t{3,3}	s{3,4} s{31,1}
		=	=	=				= or	= or	=
Duals to uniform polyhedra
V43	V3.82	V(3.4)2	V4.62	V34	V3.43	V4.6.8	V34.4	V33	V3.62	V35

It is also one of the simplest examples of a hypersimplex, a polytope formed by certain intersections of a hypercube with a hyperplane.

The octahedron is topologically related as a part of sequence of regular polyhedra with Schläfli symbols {3,n}, continuing into the hyperbolic plane.

*n32 symmetry mutation of regular tilings: {3,n} v t e
Spherical	Euclid.	Compact hyper.	Paraco.	Noncompact hyperbolic
3.3	33	34	35	36	37	38	3∞	312i	39i	36i	33i

Tetratetrahedron[edit]

The regular octahedron can also be considered a rectified tetrahedron – and can be called a tetratetrahedron. This can be shown by a 2-color face model. With this coloring, the octahedron has tetrahedral symmetry.

Compare this truncation sequence between a tetrahedron and its dual:

Family of uniform tetrahedral polyhedra
Symmetry: [3,3], (*332)	[3,3]+, (332)
{3,3}	t{3,3}	r{3,3}	t{3,3}	{3,3}	rr{3,3}	tr{3,3}	sr{3,3}
Duals to uniform polyhedra
V3.3.3	V3.6.6	V3.3.3.3	V3.6.6	V3.3.3	V3.4.3.4	V4.6.6	V3.3.3.3.3

The above shapes may also be realized as slices orthogonal to the long diagonal of a tesseract. If this diagonal is oriented vertically with a height of 1, then the first five slices above occur at heights r, 3/8, 1/2, 5/8, and s, where r is any number in the range 0 < r ≤ 1/4, and s is any number in the range 3/4 ≤ s < 1.

The octahedron as a tetratetrahedron exists in a sequence of symmetries of quasiregular polyhedra and tilings with vertex configurations (3.n)², progressing from tilings of the sphere to the Euclidean plane and into the hyperbolic plane. With orbifold notation symmetry of *n32 all of these tilings are Wythoff constructions within a fundamental domain of symmetry, with generator points at the right angle corner of the domain.^[9][10]

*n32 orbifold symmetries of quasiregular tilings: (3.n)2
Construction	Spherical	Euclidean	Hyperbolic
*332	*432	*532	*632	*732	*832…	*∞32
Quasiregular figures
Vertex	(3.3)2	(3.4)2	(3.5)2	(3.6)2	(3.7)2	(3.8)2	(3.∞)2

Trigonal antiprism[edit]

As a trigonal antiprism, the octahedron is related to the hexagonal dihedral symmetry family.

Uniform hexagonal dihedral spherical polyhedra
Symmetry: [6,2], (*622)	[6,2]+, (622)	[6,2+], (2*3)
{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{6,2}	tr{6,2}	sr{6,2}	s{2,6}
Duals to uniforms
V62	V122	V62	V4.4.6	V26	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Family of uniform n-gonal antiprisms

Antiprism name	Digonal antiprism	(Trigonal) Triangular antiprism	(Tetragonal) Square antiprism	Pentagonal antiprism	Hexagonal antiprism	Heptagonal antiprism	Octagonal antiprism	Enneagonal antiprism	Decagonal antiprism	Hendecagonal antiprism	Dodecagonal antiprism	…	Apeirogonal antiprism
Polyhedron image												…
Spherical tiling image												Plane tiling image
Vertex config.	2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	…	∞.3.3.3

Square bipyramid[edit]

«Regular» right (symmetric) n-gonal bipyramids:

Bipyramid name	Digonal bipyramid	Triangular bipyramid (See: J12)	Square bipyramid (See: O)	Pentagonal bipyramid (See: J13)	Hexagonal bipyramid	Heptagonal bipyramid	Octagonal bipyramid	Enneagonal bipyramid	Decagonal bipyramid	…	Apeirogonal bipyramid
Polyhedron image										…
Spherical tiling image										Plane tiling image
Face config.	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	…	V∞.4.4
Coxeter diagram										…

[edit]

Truncation of two opposite vertices results in a square bifrustum.

The octahedron can be generated as the case of a 3D superellipsoid with all exponent values set to 1.

See also[edit]

• Octahedral number
• Centered octahedral number
• Spinning octahedron
• Stella octangula
• Triakis octahedron
• Hexakis octahedron
• Truncated octahedron
• Octahedral molecular geometry
• Octahedral symmetry
• Octahedral graph
• Octahedral sphere

References[edit]

External links[edit]

• «Octahedron» . Encyclopædia Britannica. Vol. 19 (11th ed.). 1911.
• Weisstein, Eric W. «Octahedron». MathWorld.
• Klitzing, Richard. «3D convex uniform polyhedra x3o4o – oct».
• Editable printable net of an octahedron with interactive 3D view
• Paper model of the octahedron
• K.J.M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
• The Uniform Polyhedra
• Virtual Reality Polyhedra – The Encyclopedia of Polyhedra
  • Conway Notation for Polyhedra – Try: dP4

v t e Fundamental convex regular and uniform polytopes in dimensions 2–10
Family	An	Bn	I2(p) / Dn	E6 / E7 / E8 / F4 / G2	Hn
Regular polygon	Triangle	Square	p-gon	Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	Pentachoron	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	122 • 221
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	132 • 231 • 321
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	142 • 241 • 421
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
Uniform n-polytope	n-simplex	n-orthoplex • n-cube	n-demicube	1k2 • 2k1 • k21	n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds