Как рассчитать площадь четырехугольника
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Через диагонали и угол между ними
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
Через стороны и противолежащие углы
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
Площадь вписанного четырехугольника в окружность
Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
Площадь описанного четырехугольника около окружности через радиус
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
Площади четырехугольников
| Формулы для площадей четырехугольников |
| Вывод формул для площадей четырехугольников |
| Вывод формулы Брахмагупты для площади вписанного четырехугольника |
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
a и b – смежные стороны
d – диагональ,
φ – любой из четырёх углов между диагоналями
Получается из верхней формулы подстановкой d=2R
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
a – сторона,
ha – высота, опущенная на эту сторону
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
a – сторона,
ha – высота, опущенная на эту сторону
a – сторона,
φ – любой из четырёх углов ромба
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
a и b – основания,
c и d – боковые стороны
a и b – неравные стороны,
φ – угол между ними
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними
,
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,
Формулу называют «Формула Брахмагупты»
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник | S = ab | ||
| Параллелограмм | |||
| Квадрат | S = a 2 | ||
| S = 4r 2 | |||
| Ромб | |||
| Трапеция | |||
| S = m h | |||
| Дельтоид | S = ab sin φ | ||
| Произвольный выпуклый четырёхугольник | |||
| Вписанный четырёхугольник |
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
Получается из верхней формулы подстановкой d = 2R
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
r – радиус вписанной окружности
φ – любой из четырёх углов между ними
,
где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
| Прямоугольник | |
| Параллелограмм | |
| Квадрат | |
| S = a 2
где |
|
| S = 4r 2 | |
| Ромб | |
| Трапеция | |
| Дельтоид | |
|
где |
|
| Произвольный выпуклый четырёхугольник | |
| Вписанный четырёхугольник | |
где
a и b – смежные стороны
где
d – диагональ,
φ – любой из четырёх углов между диагоналями
где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями
Формула получается из верхней формулы подстановкой d = 2R
Параллелограмм
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a и b – смежные стороны,
φ – угол между ними
φ – любой из четырёх углов между ними
Квадрат
где
a – сторона квадрата
Получается из верхней формулы подстановкой d = 2R
Ромб
где
a – сторона,
ha – высота, опущенная на эту сторону
где
a – сторона,
φ – любой из четырёх углов ромба
где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба
Трапеция
где
a и b – основания,
h – высота
φ – любой из четырёх углов между ними
где
a и b – основания,
c и d – боковые стороны ,
Дельтоид
где
a и b – неравные стороны,
φ – угол между ними
где
a и b – неравные стороны,
φ1 – угол между сторонами, равными a ,
φ2 – угол между сторонами, равными b .
где
a и b – неравные стороны,
r – радиус вписанной окружности
Произвольный выпуклый четырёхугольник
φ – любой из четырёх углов между ними
Вписанный четырёхугольник
где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр
Формулу называют «Формула Брахмагупты»
Вывод формул для площадей четырехугольников
Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле
Доказательство . В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле
где a – сторона параллелограмма, а ha – высота высота высота , опущенная на эту сторону (рис. 2).
Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
что и требовалось доказать.
Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
то, в силу утверждения 2, справедлива формула
что и требовалось доказать.
Утверждение 4 . Площадь ромба ромба можно найти по формуле
,
где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
что и требовалось доказать.
Утверждение 5 . Площадь трапеции можно найти по формуле
,
где a и b – основания трапеции, а h – высота высота высота (рис.5).
Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому
что и требовалось доказать.
Утверждение 6 . Площадь трапеции трапеции можно найти по формуле
где a и b – основания, а c и d – боковые стороны трапеции ,
(рис.6).
Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):
,
что и требовалось доказать.
Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
Калькулятор расчета площади четырехугольника
В публикации представлены онлайн-калькуляторы и формулы для расчета площади выпуклого четырехугольника по разным исходным данным: через диагонали и угол между ними, по всем сторонам (если вокруг можно описать окружность), по полупериметру и радиусу вписанной окружности.
Расчет площади
Инструкция по использованию: введите известные значения, затем нажмите кнопку “Рассчитать”. В результате будет вычислена площадь фигуры с учетом указанных данных.
1. Через диагонали и угол между ними
Формула расчета
2. По всем сторонам (формула Брахмагупты)
Примечание: Если вокруг четырехугольника можно описать окружность.
Формула расчета
p – полупериметр четырехугольника, равняется:
http://www.resolventa.ru/spr/planimetry/sqf.htm
Как рассчитать площадь четырехугольника
На данной странице калькулятор поможет рассчитать площадь четырехугольника онлайн. Для расчета задайте длину сторон, длины диагоналей и угол между ними, противолежащие углы, радиус окружности.
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Через диагонали и угол между ними
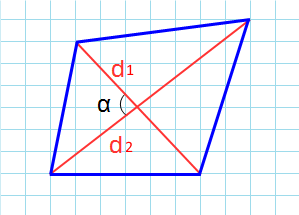
Формула для нахождения площади четырехугольников через диагонали и угол между ними:
d1, d2 — диагонали; α — угол между диагоналями.
Через стороны и противолежащие углы
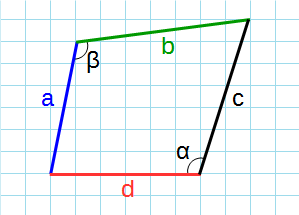
Формула для нахождения площади четырехугольников через стороны и противолежащие углы:
p — полупериметр четырехугольника; a, b, c, d — стороны четырехугольника; α, β — противолежащие углы.
Площадь вписанного четырехугольника в окружность
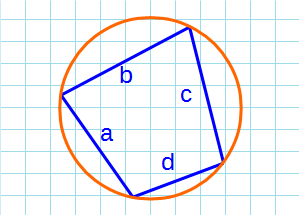
Формула Брахмагупты для нахождения площади вписанного четырехугольника в окружность:
p — полупериметр четырехугольника; a, b, c, d — стороны четырехугольника.
Площадь описанного четырехугольника около окружности через радиус
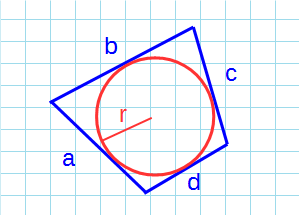
Формула для нахождения площади описанного четырехугольника около окружности через радиус:
p — полупериметр четырехугольника; r — радиус вписанной окружности; a, b, c, d — стороны четырехугольника.
Площадь описанного четырехугольника около окружности через стороны и противолежащие углы
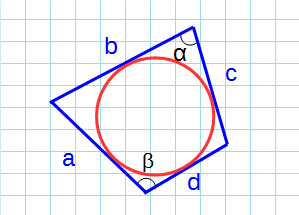
Формула для нахождения площади описанного четырехугольника около окружности через стороны и противолежащие углы:
p — полупериметр четырехугольника; a, b, c, d — стороны четырехугольника; α, β — противолежащие углы.
Свойства вписанных и описанных четыехугольников
Содержание:
- Вписанный четырехугольник, особенности, основные свойства фигуры
- Описанный четырехугольник, особенности, основные свойства фигуры
- Площадь четырехугольника связана с радиусом вписанной в него окружности формулой
- Чему равна сумма противоположных углов вписанного в окружность четырехугольника
- Как найти радиус вписанного в окружность четырехугольника, формула
Вписанный четырехугольник, особенности, основные свойства фигуры
Вписанный в окружность четырехугольник является таким четырехугольником, каждая из вершин которого принадлежит описанной около него окружности.
Вписанный в окружность четырехугольник изображен на рисунке:
Здесь около четырехугольника ABCD описана окружность, а сам этот четырехугольник можно назвать вписанным в данную окружность. Этот вывод можно сделать на основании определения, рассмотренного ранее, так как точки A, B, C, D являются одновременно и вершинами четырехугольника, и принадлежат описанной около него окружности.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Теорема 1
Какой-либо четырехугольник может быть вписан в некую окружность при условии, что его противолежащие углы в сумме дают 180°.
Теорема 2
В том случае, когда противолежащие углы некого четырехугольника в сумме составляют 180°, данный четырехугольник может быть вписан в окружность.
На примере рисунка запишем смысл изложенной теоремы:
(left. begin{array}{l} angle A + angle C = {180^o}\ angle B + angle D = {180^o} end{array} right} Leftrightarrow ABCD) треугольник вписан в окружность.
Следствие 1
Не каждый параллелограмм допустимо вписывать в окружность, лишь прямоугольники — в том числе квадраты.
Если какой-то четырехугольник вписан в окружность, то ее центральная точка совпадет с точкой, в которой пересекаются диагонали вписанного четырехугольника. При этом радиус описанной около четырехугольника окружности составит половину от длины его диагонали, то есть:
(R = frac{1}{2}BD)
Радиус, окружности, описанной около некого четырехугольника с прямыми углами, можно вычислить с помощью следующей формулы, содержащей стороны прямоугольника:
(R = frac{1}{2}sqrt {A{B^2} + A{D^2}}.)
Представим, что прямоугольник имеет стороны, которые равны a и b. Тогда справедливо следующее соотношение:
(R = frac{1}{2}sqrt {{a^2} + {b^2}})
Следствие 2
Допустимо вписать в окружность лишь такую трапецию, которая является равнобедренной.
Выведем формулу для вычисления радиуса окружности, которая описана около равнобедренной трапеции. Искомая величина равна радиусу окружности, описанной около одного из треугольников, имеющего те же вершины, что и рассматриваемая трапеция:
ABC, ABD, ACD или BCD.
Описанный четырехугольник, особенности, основные свойства фигуры
Описанным четырехугольником называют такую геометрическую фигуру с четырьмя углами, каждая из сторон которой является касательной к окружности. Данная окружность считается вписанной в рассматриваемый четырехугольник.
Теорема 3
В любой четырехугольник допустимо вписать какую-либо окружность при условии, что его противолежащие стороны в сумме равны.
Заметим, что в данном случае соблюдено условие:
AB+CD=BC+AD
На основе теоремы можно сформулировать обратное утверждение. В том случае, когда противоположные стороны четырехугольника в сумме равны, то есть AB+CD=BC+AD, в такой четырехугольник ABCD допустимо вписать какую-либо окружность.
Теорема 4
Центральная точка окружности, вписанной в четырехугольник, совпадает с точкой, в которой пересекаются биссектрисы данной геометрической фигуры.
Заметим, что на рисунке биссектрисами углов, которые имеет четырехугольник ABCD, являются следующие отрезки:
- AO;
- BO;
- CO;
- DO.
В результате:
(angle BAO = angle DAO)
(angle ABO = angle CBO) и так далее.
Теорема 5
Точки, в которых вписанная окружность касается описанного четырехугольника, расположены на сторонах с началом, совпадающим с одной вершиной, и находятся на одинаковом удалении от данной вершины.
Рассмотрим рисунок. Заметим, что:
BM=BK;
CK=CF;
DF=DN.
Записанные равенства вытекают из того факта, что это отрезки касательных, которые проведены из одной точки.
Запишем следующие соотношения:
(OM bot AB);
(OK bot BC);
(OF bot CD);
(ON bot AD).
Данные соотношения верны, так как включают в себя радиусы, которые проведены в точки касания окружности и описанного четырехугольника.
Площадь четырехугольника связана с радиусом вписанной в него окружности формулой
В том случае, когда в четырехугольник вписана окружность, его площадь определяется по формуле:
(S = p cdot r)
Здесь p обозначает полупериметр четырехугольника.
Вспомним, что противолежащие стороны четырехугольника, в который вписана окружность, в сумме равны. Исходя из данного утверждения, можно сделать вывод: полупериметр такого четырехугольника равен какой-либо из пар сумм противолежащих сторон.
Если рассмотреть некий четырехугольник ABCD, то можно записать формулу для вычисления полупериметра этой геометрической фигуры:
p=AD+BC
p=AB+CD.
Тогда площадь четырехугольника, в который вписана окружность, будет вычислена таким образом:
({S_{ABCD}} = (AD + BC) cdot r;)
({S_{ABCD}} = (AB + CD) cdot r.)
В результате для определения радиуса окружности, которая вписана в некий четырехугольник, можно воспользоваться следующей формулой:
(r = frac{S}{p}.)
В том случае, если рассматривается описанная около четырехугольника ABCD окружность, то формула для вычисления ее радиуса примет вид:
(r = frac{{{S_{ABCD}}}}{{AD + BC}};)
(r = frac{{{S_{ABCD}}}}{{AB + CD}}.)
Чему равна сумма противоположных углов вписанного в окружность четырехугольника
Теорема 6
Если четырехугольник вписан в некую окружность, то его противолежащие углы в сумме дают .
Заметим, что на рисунке изображен четырехугольник ABCD, вписанный в окружность (O; R). Требуется доказать, что:
(angle A+angle C=180^o;)
(angle B+angle D=180^o.)
Представим доказательства. По условию:
(angle A) — угол вписанного четырехугольника, опирается на дугу BCD;
(angle C) — угол, который опирается на дугу DAB.
Зная, что вписанный угол составляет ½ часть дуги, которая является его опорой, запишем:
(angle A = frac{1}{2} cup BCD,)
(angle C = frac{1}{2} cup DAB.)
В результате:
(angle A + angle C = frac{1}{2} cup BCD + frac{1}{2} cup DAB = frac{1}{2}( cup BCD + cup DAB) = frac{1}{2} cdot 360^o = 180^o.)
Аналогичным образом запишем, что:
(angle B + angle D = frac{1}{2}( cup CDA + cup ABC) = frac{1}{2} cdot 360^o = 180^o.)
Теорема доказана.
Теорема 7
Если имеется такой четырехугольник, в котором противолежащие углы в сумме составляют (180^o), то около него можно описать окружность.
Представим, что имеется некий четырехугольник ABCD.
Сумма его противолежащих углов равна: (angle B+angle D=180^o).
Попробуем доказать, что около рассматриваемого четырехугольника можно описать окружность.
В первую очередь построим окружность около треугольника ABC таким образом, чтобы точка D принадлежала данной окружности. Построим доказательства, двигаясь «от обратного».
Допустим, что точка D не принадлежит окружности, которая описана около треугольника ABD. В таком случае точка D должна располагаться во внутренней области, ограниченной данной окружностью, или за пределами окружности.
В том случае, когда точка D расположена во внутреннем пространстве, ограниченном окружностью, какой-то луч AD имеет точку пересечения с окружностью. Обозначим ее, как Е. Заметим, что если вокруг четырехугольника ABCE описана окружность, то его противолежащие углы в сумме составляют (180^o):
(angle B+angle E = 180^o.)
Согласно данным из условия задачи:
(angle B+angle D=180^o.)
Таким образом:
(angle D=angle E.)
С другой стороны, угол D является внешним углом треугольника DCE при его вершине D. Исходя из этого, запишем:
(angle ADC=angle DEC+angle DCE.)
В результате получается, что угол D не равен углу E. Это утверждение противоречиво. Таким образом, точка D не расположена во внутреннем пространстве, ограниченном окружностью, описанной около треугольника ABC.
Луч AD имеет точку пересечения с окружностью, обозначенную буквой Е. В таком случае, ABCE представляет собой вписанный в окружность четырехугольник, а также:
(angle B+angle E=180^o)
Согласно условию задачи:
(angle B+angle D=180^o.)
Тогда:
(angle D=angle E.)
Однако угол Е является внешним углом треугольника ECD и расположен при вершине E.
Таким образом: (angle AEC=angle EDC+angle DCE.)
В результате недопустимо равенство углов D и E. В том случае, когда точка D расположена за пределами окружности, возникает противоречие. Таким образом, остается единственно верный вариант расположения этой точки, согласно которому она принадлежит окружности, описанной около четырехугольника. Теорема доказана.
Согласно свойству и признаку четырехугольника, вписанного в окружность, необходимым и достаточным условием вписанного четырехугольника является следующая теорема.
Теорема 7
Около четырехугольника допустимо описать окружность лишь в том случае, когда его противолежащие углы в сумме составляют 180 градусов.
Как найти радиус вписанного в окружность четырехугольника, формула
Допустим, что имеется некий четырехугольник, стороны которого обозначены, как a, b, c, d, а полупериметр равен p. В таком случае описанная около данного четырехугольника окружность имеет радиус, который можно рассчитать по формуле как отношение:
(R={frac {1}{4}}{sqrt {frac {(ab+cd)(ac+bd)(ad+bc)}{(p-a)(p-b)(p-c)(p-d)}}}.)
Примечание
Формулу радиуса окружности, которая описана около четырехугольника, ввел индийский математик Ватассери Парамешвара в XV веке.
Рассмотрим еще одну закономерность, которую называют формулой Брахмагупты. С ее помощью можно определить площадь S четырехугольника, который вписан в окружность и имеет стороны, равные a, b, c, d:
(S={sqrt {(p-a)(p-b)(p-c)(p-d)}}.)
В данном случае p является полупериметром, то есть в два раза меньше, чем периметр, и определяется как:
(p={tfrac {1}{2}}(a+b+c+d).)
С помощью формулы Брахмагупты представляется возможным изменить форму записи формулы Парамешвары:
(4SR={sqrt {(ab+cd)(ac+bd)(ad+bc)}}.)
Здесь S определяется, как площадь четырехугольника, вписанного в окружность. Диаметр равен двум радиусам и проходит через центр окружности.
