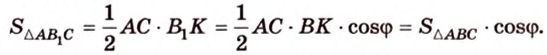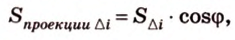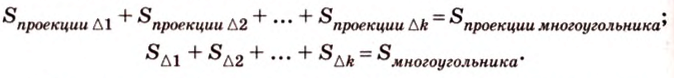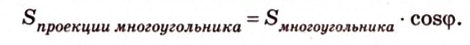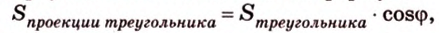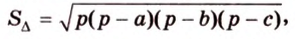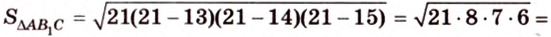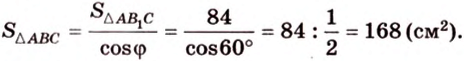§ 17.Площадь ортогональной проекции многоугольника
Из свойств параллельного проектирования (§ 12) следует, что если фигура лежит в плоскости, параллельной плоскости проекций, то ортогональной проекцией этой фигуры является равная ей фигура.
Рис. 109
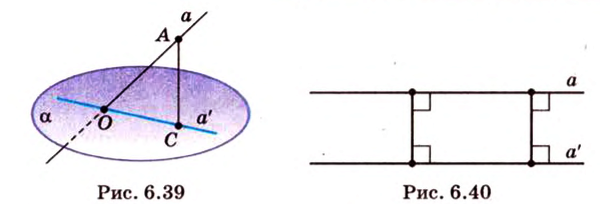
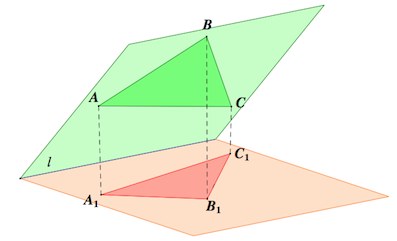
Рассмотрим вопрос о площади ортогональной проекции многоугольника, расположенного в плоскости α, которая образует угол ϕ (0° < ϕ < 90°) с плоскостью проекций π и пересекает её по прямой l (см. рис. 109). Предварительно рассмотрим ортогональное проектирование отрезка, лежащего в плоскости α, выделив два случая расположения этого отрезка относительно прямой l = α ∩ π.
Случай 1. AB ‖ l (см. рис. 109). Отрезок A1B1, являющийся ортогональной проекцией отрезка AB, равен и параллелен отрезку AB (§ 12).
Случай 2. CD ⊥ l (см. рис. 109). По теореме о трёх перпендикулярах прямая C1D1, являющаяся ортогональной проекцией прямой CD, также перпендикулярна прямой l. Следовательно, ∠ CEC1 — угол между плоскостью α и плоскостью проекций π, т. е. 



| C1D1 | = | CD|•cos ϕ.(1)
Теперь рассмотрим вопрос об ортогональном проектировании многоугольника.

Рис. 110
Рис. 111



На основании выше рассмотренных свойств ортогональной проекции отрезка имеем:
AC ‖ l ⇒ A1C1 ‖ l; AC = A1C1; B1H1 = BH•cos ϕ.
По теореме о трёх перпендикулярах прямая B1H1 — ортогональная проекция прямой BH — перпендикулярна прямой l, следовательно, отрезок B1H1 — высота треугольника A1B1C1. Поэтому
S⧌ A1B1C1 = 

Таким образом,
S⧌ A1B1C1 = S⧌ ABC•cos φ.(2)
б) Ни одна из сторон проектируемого треугольника ABC не параллельна прямой l (рис. 111).
Проведём через каждую вершину треугольника прямую, параллельную прямой l. Одна из этих прямых лежит между двумя другими (на нашем рисунке — это прямая m), и, следовательно, разбивает треугольник ABC на треугольники ABD и ACD с высотами соответственно BH и CE, проведёнными к их общей стороне AD (или её продолжению), которая параллельна l.
Рис. 112
Прямая m1 — ортогональная проекция прямой m — также разбивает треугольник A1B1C1 — ортогональную проекцию треугольника ABC — на треугольники A1B1D1 и A1C1D1, где A1D1 ‖ l, B1H1 ⊥ A1D1, C1E1 ⊥ A1D1. Принимая во внимание (1) и (2), получаем:
S⧌ A1B1C1 = S⧌ A1B1D1 + S⧌ A1C1D1 =
= S⧌ ABC•cos ϕ + S⧌ ACD•cos ϕ =
= (S⧌ ABD + S⧌ ACD)•cos ϕ = S⧌ ABC•cos ϕ.
Итак, для произвольно расположенного в плоскости α треугольника ABC выполняется
S⧌ A1B1C1 = S⧌ ABC•cos φ.(3)
2. Площадь проекции многоугольника. Пусть Ф — данный выпуклый многоугольник ABCDEF (рис. 112), расположенный в плоскости α. Его ортогональную проекцию — многоугольник A1B1C1D1E1F1 — обозначим Ф1.
Проведя из вершины A многоугольника Ф все его диагонали, разобьём этот многоугольник в объединение непересекающихся треугольников ABC, ACD, ADE и AEF и обозначим их площади соответственно S1, S2, S3 и S4. Тогда для площади SФ многоугольника Ф выполняется
SФ = S1 + S2 + S3 + S4.(4)
Аналогичным образом многоугольник Ф1 разобьём в объединение треугольников A1B1C1, A1C1D1, A1D1E1 и A1E1F1, площади которых обозначим соответственно 



Тогда для площади 





Принимая во внимание (2), (3) и (4), находим





Разбивая указанным способом на треугольники любой n-угольник Ф, получим аналогичное соотношение между площадью S(Ф) этого n-угольника и площадью S(Ф1) его проекции Ф1:
S(Ф1) = S(Ф)•cos ϕ,
где ϕ — угол между плоскостью данного n-угольника и плоскостью проекций. Теорема доказана. ▼
В школьном курсе геометрии изучаются выпуклые многоугольники. Вместе с тем заметим, что доказанная теорема справедлива и для невыпуклых многоугольников.
Задания для работы с интернет-ресурсами
1. Распечатайте рисунки по теме «Плоскости в пространстве», «Параллельные плоскости», «Пересечение плоскостей», на них найдите параллельные и пересекающиеся плоскости, постройте прямые, по которым пересекаются пары плоскостей. На изображениях куба, призмы, параллелепипеда, пирамиды найдите две параллельные плоскости, каждая из которых проходит через одну из двух изображённых скрещивающихся прямых.
2. Наберите в поисковой системе слова «Три плоскости в пространстве» и найдите рисунки, на которых изображены различные случаи расположения трёх плоскостей в пространстве. Обратите внимание на различное расположение трёх плоскостей, среди которых нет пар параллельных плоскостей. Найдите материал об отрезках, образованных при пересечении двух прямых тремя параллельными плоскостями, вы получите пространственный аналог теоремы Фалеса. Найдите материал о жизни и творчестве Фалеса Милетского.
3. Найдите и рассмотрите рисунки по темам «Угол между плоскостями», «Двугранный угол», «Линейный угол двугранного угла», «Перпендикулярные плоскости», «Две плоскости, перпендикулярные третьей», «Отвес», «Отвесная стена», они помогут вам для построения рисунков к задачам.
4. Найдите материал по темам «Общий перпендикуляр двух скрещивающихся прямых», «Расстояние между двумя скрещивающимися прямыми». Посмотрите рисунки на сайтах:
http://school-collection.edu.ru/,
webmath.exponenta.ru/.
5. Посмотрите в Интернете материалы по теме «Теорема о площади ортогональной проекции многоугольника». Обратите внимание на рисунки и решения наиболее типичных задач по этой теме. Попытайтесь некоторые из этих задач решить самостоятельно.
6. а) Распечатайте рисунок правильного тетраэдра из Интернета. Проведите через ребро основания этого тетраэдра сечение, перпендикулярное двум его боковым граням.
б) На распечатанном рисунке куба найдите две плоскости, одна из которых проходит через концы трёх рёбер куба, имеющих общую вершину, а другая — через концы трёх рёбер, исходящих из противоположной его вершины. Определите угол между этими плоскостями.
Вопросы для самооценки
1. Оцените результаты изучения этой главы. Довольны ли вы ими?
2. Что нового вы узнали в этой главе?
3. Как могут пригодиться вам эти знания в повседневной жизни?
4. Какие задания в этой главе были для вас самыми трудными? Почему?
5. Использовали ли вы при выполнении заданий дополнительные источники: справочники, пособия, интернет-ресурсы?
6. Обращались ли вы за помощью к одноклассникам, родителям, учителю?
Ортогональное проецирование — определение и вычисление с примерами решения
Ортогональное проецирование:
Параллельное проецирование, направление которого перпендикулярно плоскости проекции, называется ортогональным проецированием. Проекция фигуры, образующаяся при ортогональном проецировании, называется ортогональной проекцией, или просто проекцией этой фигуры.
Поскольку ортогональное проецирование является особым видом параллельного проецирования, то для него выполняются все свойства последнего. Ортогональной проекцией прямой
Отметим, что прямые, перпендикулярные одной из параллельных плоскостей, перпендикулярны и остальным, поэтому ортогональное проецирование на одну из таких плоскостей будет ортогональным и на остальные плоскости. Очевидно, что ортогональные проекции фигуры на параллельные плоскости равны между собой.
Ортогональное проецирование также имеет только ему присущие свойства. Одно из них выражает теорема о площади ортогональной проекции многоугольника.
Площадь ортогональной проекции
Теорема 5
Площадь ортогональной проекции произвольного многоугольника на плоскость равна произведению площади самого многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции.
Как пример многоугольника возьмем 
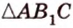
о трех перпендикулярах 
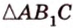
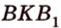
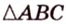
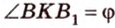
Учитывая, что 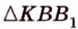
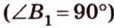
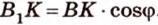
Итак, 
Чтобы доказать теорему для произвольного многоугольника, его разбивают на треугольники. Тогда для каждого треугольника и его проекции можно записать равенство
где 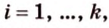
Получим в левой части равенства площадь проекции многоугольника, а в правой — площадь самого многоугольника, умноженную на косинус угла между их плоскостями. Отсюда
Т.е. и для этого случая теорема истинна.
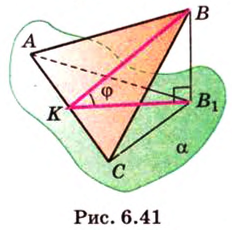
Пример:
Ортогональной проекцией треугольника является треугольник со сторонами 13 см, 14 см и 15 см. Плоскость треугольника образует с плоскостью проекции угол 60°. Вычислите площадь данного треугольника.
Воспользуемся рисунком 6.41. Известно, что площадь проекции треугольника вычисляют по формуле:
где 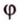
По формуле Герона найдем площадь 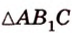
где 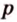
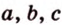
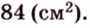
Тогда
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Декартовы координаты на плоскости
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
- Планиметрия — формулы, определение и вычисление
- Параллельность прямых и плоскостей
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Презентация по теме «Площадь ортогональной проекции», 10 класс
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Снятие эмоционального напряжения
у детей и подростков с помощью арт-практик
и психологических упражнений»
Сертификат и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Площадь ортогональной проекции 30.04.2020
Время выполнения работ по ЕГЭ
Решение задач: № 46 Равнобедренные треугольники АВС и ABD с общим основанием АВ лежат в различных плоскостях, угол между которыми равен а. Найдите cosα, если: 1) АВ = 24 см, АС = 13 см, AD = 37 см, CD = 35 см
Решение задач: № 45 Два равнобедренных треугольника имеют общее основание, а их плоскости образуют угол 60°. Общее основание равно 16 м, боковая сторона одного треугольника 17 м, а боковые стороны другого перпендикулярны. Найдите расстояние между вершинами треугольников.
Решение задач: № 47
Формулы площадей фигур
Площадь ортогональной проекции Если угол увеличивается, то площадь ортогональной проекции — ?
Решение задач: № 48 (1) а 30 0
Домашнее задание 1
Домашнее задание: 1. Разобрать п.34, доказать теорему; 2. Решить задачу со звездочкой; 3. Решить задачи № 48(2), № 49 (1). Ответы на задания необходимо прислать до 20.00 6 мая. Удачи!
Спасибо за урок!
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 943 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 679 человек из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 306 человек из 67 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 501 085 материалов в базе
Коммуникативный педагогический тренинг: способы взаимодействия с разными категориями учащихся
Сертификат и скидка на обучение каждому участнику
Другие материалы
- 26.08.2020
- 102
- 26.08.2020
- 118
- 26.08.2020
- 119
- 26.08.2020
- 262
- 26.08.2020
- 209
- 26.08.2020
- 239
- 25.08.2020
- 349
- 25.08.2020
- 219
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 26.08.2020 2044 —> —> —> —>
- PPTX 1.7 мбайт —> —>
- Оцените материал:
Настоящий материал опубликован пользователем Мяснова Светлана Александровна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 6 месяцев
- Подписчики: 1
- Всего просмотров: 44749
- Всего материалов: 66
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
День памяти жертв холокоста включен в примерный план воспитательной работы
Время чтения: 1 минута
Учителя и воспитатели детсадов Подмосковья будут получать дополнительно 5 тыс. рублей
Время чтения: 1 минута
Большинство российских вузов используют смешанный формат обучения
Время чтения: 1 минута
Большинство российских школьников недовольны качеством питания в столовых
Время чтения: 1 минута
В Петербурге введут новые COVID-ограничения для несовершеннолетних
Время чтения: 2 минуты
Минспорта утвердило программу подготовки киберспортсменов
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Стереометрия. Страница 4
1 2 3 4 5 6 7 8
1. Декартовы координаты в пространстве
Пусть заданы три взаимно перпендикулярные прямы x,y,z (Рис.1). Если провести через каждую пару прямых плоскость, то получим три взаимно перпендикулярные плоскости xy,xz,yz. Тогда прямые x,y,z будут называться осями координат, а точка пересечения О началом координат. Каждую ось точка О разбивает на две полуоси: положительную и отрицательную.
Возьмем теперь произвольную точку, например точку А. Тогда для того, чтобы определить координаты точки А, необходимо провести три плоскости, проходящие через точку А и параллельные плоскостям XY, XZ, YZ. Точки пересечения этих плоскостей с осями координат Аx, Ay, Az и будут являться координатами точки А, которые записываются так: А (Ax, Ay, Az).
Рис. 1 Декартовы координаты в пространстве.
2.Расстояние между двумя точками
Пусть задана декартова система координат с осями X, Y, Z (Рис.2). Необходимо найти расстояние между двумя точками А (x1;y1;z1) и В (x2;y2;z2).
Проведем два перпендикуляра от точек А и В на плоскость XY. Они пересекут плоскость XY в точках A’ и B’. Теперь проведем плоскость через точку А и параллельную плоскости XY. Тогда расстояние между точками по теореме Пифагора будет равно:
AB 2 = AC 2 + BC 2
Таким образом, расстояние между двумя точками вычисляется по следующей формуле:
Рис.2 Расстояние между двумя точками
3. Преобразование симметрии в пространстве
Преобразование фигур в пространстве определяется таким же образом, как и преобразование фигур на плоскости (Рис.3). Помимо преобразования относительно точки и преобразования относительно прямой, в пространстве рассматривают преобразование относительно плоскости.
Пусть в пространстве задана плоскость α. В не этой плоскости задан квадрат со сторонами АВСD. Каждую точку нашей фигуры проецируем на плоскость α. А затем откладываем такое же расстояние по другую стороны плоскости и получаем преобразованную фигуру A»B»C»D». Таким образом, точки A»B»C»D» симметричны точкам ABCD относительно плоскости так же, как и все точки квадрата ABCD. Такое преобразование называется преобразованием относительно плоскости. А плоскость называется плоскостью симметрии. Если точка принадлежит плоскости α, то она переходит в саму себя.
Рис. 3 Преобразование симметрии в пространстве.
4. Движение в пространстве
Движение в пространстве определяется таким же образом, как и на плоскости. При движении в пространстве сохраняются расстояния между точками. И так же, как и на плоскости, прямые переходят в прямые, отрезки в отрезки, углы между полупрямыми сохраняются. Новым свойством, которым обладает движение в пространстве, являются то, что при движении плоскость переходит в плоскость.
Пусть задана плоскость α. Отметим на ней точки А,В,С не лежащие на одной прямой и построим на них треугольник (Рис.4). При движении эти точки передут в точки A’, B’, C’ также не лежащие на одной прямой. Проведем на плоскости α прямую, перескающую треугольник в точках X и Y и отметим на ней точку Z. При движении точки X и Y передут в точки X’ и Y’, прямая а передет в прямую a’. Следовательно она будет принадлежать плоскости α’. Таким образом, плоскость α переходит в плоскость α’. При движении фигур в пространстве, две фигуры называются равными, если они переходят сами в себя, т.е. совмещаются.
Рис. 4 Движение в пространстве.
Параллельный перенос
Параллельным переносом в пространстве называется такое преобразование фигуры, при котором все ее точки с координатами (z; y; z) переходят в точки с координатами (x+a; y+b; z+c), где a, b, c — постоянные числа.
Парралельный перенос в пространстве задается формулами:
x’ = x + a
y’ = y + b
z’ = z + c
Подобие пространственных фигур
Преобразование подобия фигур в пространстве (гомотетия) определяется таким же образом, как и на плоскости. (Рис. 4.1)
При преобразования подобия расстояние между точками изменяется в одно и тоже число раз. Прямые переходят в прямые, полупрямые в полупрямые, отрезки в отрезки. Углы между полупрямыми сохраняются. При преобразовании подобия плоскость, не проходящая через центр гомотетии, переходит в параллельную плоскость. Так же, как и на плоскости преобразование подобия с коэффициентом гомотетии k переводит точки A и B в точки A’ и B’, отрезок АВ в отрезок A’B’ = k AB.
Рис. 4.1 Подобие пространственных фигур.
5. Угол между прямой и плоскостью
Пусть задана плоскость α. Прямая с пересекает плоскость α в точке А (Рис.5). Точка А лежит на прямой c’. Прямая c’ называется проекцией прямой с на плоскость α. Таким образом, углом между прямой и плоскостью является угол между прямой и ее проекцией на данную плоскость. Т.е. угол между прямой с и c’.
Если прямая будет перпендикулярна плоскости, то угол между прямой и плоскостью будет составлять 90°. Если параллельна — то 0°.
Рис. 5 Угол между прямой и плоскостью.
6. Угол между плоскостями
Пусть заданы две пересекающиеся плоскости α и β (Рис.6). Проведем плоскость γ, которая перпендикулярна их прямой пересечения с. Плоскость γ пересекает данные плоскости по прямым а и b. Угол между прямыми а и b и есть угол между данными плоскостями α и β.
Возьмем другую секущую плоскость γ’, которая параллельна γ и перпендикулярна прямой с. Она пересечет плоскости α и β по прямым a’ и b’. Если мы выполним параллельный перенос плоскости γ вдоль прямой с, то т.к. прямые а и a’ находятся в одной плоскости α и перпендикулярны прямой с, следовательно они совпадут. Таким образом, угол между плоскостями не зависит от секущей плоскости.
Рис. 6 Угол между плоскостями.
7. Векторы в пространстве
Так же, как и на плоскости, в пространстве вектор — это направленный отрезок. Любой вектор имеет абсолютную величину и направление. Каждый вектор имеет три координаты а (x; y; z) (Рис.7).
Если вектор имеет начальную и конечную точки А и В, то его координатами будут числа: АВ (x2 — x1; y2 — y1; z2 — z1). Вектора с равными координатами равны.
Действия над векторами
Действия над векторами в пространстве определяются так же, как и на плоскости.
Рис. 7 Векторы в пространстве.
8. Площадь ортогональной проекции многоугольника
Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью его проекции.
Пусть задана плоскость α. Треугольник АВС имеет сторону АВ в плоскости α и расположен под некоторым углом к этой плоскости. BF — высота треугольника АВС. По теореме о трех перпендикулярах B’F — высота треугольника AB’C. Угол ϕ между треугольником АВС и его проекцией равен углу между плоскостями, в которых они находятся, т.е. углу BFB’. Таким образом:
Если геометрическая фигура представляет собой многоугольник, то площадь ортогональной проекции можно найти, разбив его на простые треугольники, в которых хотя бы одна сторона будет параллельна плоскости проекции.
Рис. 8 Площадь ортогональной проекции многоугольника.
9. Пример 1
Докажите, что движение в пространстве переводит плоскость в плоскость.
Доказательство:
Пусть дана плоскость α. Проведем в плоскости α две пересекающиеся прямые a и b. Они пересекаются в точке О (Рис.9). Доказать, что при движении плоскость α переходит в плоскость α’.
Подвергнем две прямые а и b движению.Тогда они перейдут в прямые a’ и b’ с точкой пересечения O’. Угол ϕ между ними сохранится. Проведем через прямые a’ и b’ плоскость α’.
Если в плоскости α провести прямую с, то она пересечет прямые а и b в точках А и В. При движении прямая с перейдет в прямую с’. А точки А и В перейдут в точки A’ и B’.
Таким образом, две точки A’ и B’ принадлежат плоскости α’, так как прямая с’ пересекает прямые а’ и b’ в этих точках. А следовательно и вся прямая c’, т.е. все ее точки, принадлежат плоскости α’. Отсюда следует, что плоскость α переходит в плоскость α’.
Рис.9 Задача. Докажите, что движение в пространстве переводит плоскость в плоскость.
Пример 2
В плоскости xy найдите точку D (x; y; 0), равноудаленную от трех данных точек: А (1; 1; 1), В (1; 2; 2), С (2; 0; 1).
Решение:
Так как расстояние от точки D до точек А, В и С одинаковое, то можно составить следующие соотношения:
AD 2 = (x — 1) 2 + (y — 1) 2 + (0 — 1) 2
BD 2 = (x — 1) 2 + (y — 2) 2 + (0 — 2) 2
CD 2 = (x — 2) 2 + (y — 0) 2 + (0 — 1) 2
Приравняем первое и второе уравнения:
y 2 — 2y + 2 = y 2 — 4y + 8
Теперь приравняем второе и третье уравнения:
x 2 — 4x + 4 + y 2 + 1 = x 2 — 2x + 1 + y 2 — 4y + 4 + 4
Подставляя y = 3, получим х = 4 и D (4;3;0).
Рис.10 Задача. В плоскости xy найдите точку D (x; y; 0).
Пример 3
Докажите, что четырехугольник АВСD является параллелограммом, если: А (0; 2; 1), В (1; 1; 1), С (2; 2; 3), D (1; 3; 3).
Решение:
По свойству параллелограмма, его диагонали пересекаются в точке, которая делит их пополам. Следовательно, можно найти середины отрезков АС и BD:
xAC = (2 + 0) / 2 = 1; yAC = (2 + 2) / 2 = 2; zAC = (1 + 3) / 2 = 2
xBD = (1 + 1) / 2 = 1; yBD = (1 + 3) / 2 = 2; zBD = (3 + 1) / 2 = 2
Так как координаты середин отрезков АС и BD совпадают, то АВСD является параллелограммом (Рис. 11).
Рис.11 Задача. Докажите, что четырехугольник АВСD является параллелограммом.
Пример 4
Из точки, отстоящей от плоскости на расстоянии 4 м, проведены две наклонные, которые пересекают плоскость в точках А и В. Они образуют с плоскостью углы 45° и 30°, а между собой прямой угол. Найдите расстояние АВ между точками пересечения наклонных с плоскостью.
Решение:
Из прямоугольного треугольника СОВ (Рис.12) найдем СВ:
СВ = СО / sin 30° = 4 / 1 / 2 = 8 м.
Из прямоугольного треугольника СОА найдем СА:
АС = СО / sin 45° = 4 / 1 / = 4 м.
Теперь из прямоугольного треугольника АВС найдем АВ:
АВ 2 = CВ 2 + АС 2
АВ 2 = 8 2 + (4) 2
АВ = 4 м.
Рис.12 Задача. Из точки, отстоящей от плоскости на расстоянии 4 м.
Пример 5
Через катет равнобедренного прямоугольного треугольника проведена плоскость под углом 45° ко второму катету. Найдите угол между гипотенузой и плоскостью.
Решение:
Из прямоугольного треугольника АВО найдем ВО (Рис.13):
ВО = АВ sin 45° = АВ /
Из прямоугольного треугольника АВС найдем ВС:
ВС 2 = AB 2 + AC 2 = 2 AB 2 (т.к. АВ = АС по условию задачи)
ВС = AB
Теперь из прямоугольного треугольника ВОС найдем синус угла ВСО:
sin ∠BCO = BO / BC = АВ / / AB = 1/2
Отсюда следует, что ∠ ВСО = 30°.
Рис.13 Задача. Через катет равнобедренного прямоугольного треугольника.
http://infourok.ru/prezentaciya-po-teme-ploshad-ortogonalnoj-proekcii-10-klass-4422038.html
http://www.mathtask.ru/0063-stereometry.php
19
Фев 2014
Категория: Справочные материалы
Площадь ортогональной проекции многоугольника
2014-02-19
2014-02-19
Площадь ортогональной проекции многоугольника на плоскость равна площади проектируемого многоугольника, умноженной на косинус угла между плоскостью многоугольника и плоскостью проекций.
Докажем теорему для треугольника. Поскольку многоугольник разбивается на треугольники, сумма площадей которых есть площадь многоугольника, то и для многоугольника теорема будет верна.
Доказательство:
Пусть треугольник – проекция треугольника
на проецируемую плоскость.
Докажем, что
,
где – угол между плоскостями
Для этого разобьем треугольник на два треугольника c общей стороной
, параллельной прямой
пересечения плоскостей
. (Частный случай, когда одна из сторон треугольника
параллельна линии пересечения плоскостей
, можно рассмотреть отдельно (самостоятельно)).
Проекция треугольника – треугольник
. Причем
.
Пусть – перпендикуляр к
. Тогда по т. о трех перпендикулярах и
– перпендикуляр к
. Стало быть,
– угол между плоскостями треугольников (проецируемого и проекции).
Пусть – точка пересечения
и
,
– проекция т.
на плоскость
. Очевидно,
– высота треугольника
(
– высота треугольника
).
Из треугольника
Но и
Тогда
Имеем:
Аналогичные рассуждения – для пары треугольников и
:
(где – высота треугольника
,
– ее проекция)
Итак, суммируя площади треугольников и
соответственно, получаем
или
Что и требовалось доказать.
Пример.
Ребро куба равно 2 см. Через диагональ основания под углом к плоскости основания проведена плоскость, пересекающая боковое ребро. Найти площадь сечения.
Решение:
Пусть плоскость сечения проведена через диагональ и пересекает боковое ребро (
) в точке
.
По вышеуказанной теореме
где треугольник – проекция треугольника
на плоскость основания,
– угол между плоскостями
Ответ:
Применение теоремы можно также посмотреть, например, в этой задаче.
Автор: egeMax |
Нет комментариев
Печать страницы
Преподаватель который помогает студентам и школьникам в учёбе.
Ортогональное проецирование — определение и вычисление с примерами решения
Ортогональное проецирование:
Параллельное проецирование, направление которого перпендикулярно плоскости проекции, называется ортогональным проецированием. Проекция фигуры, образующаяся при ортогональном проецировании, называется ортогональной проекцией, или просто проекцией этой фигуры.
Поскольку ортогональное проецирование является особым видом параллельного проецирования, то для него выполняются все свойства последнего. Ортогональной проекцией прямой
Отметим, что прямые, перпендикулярные одной из параллельных плоскостей, перпендикулярны и остальным, поэтому ортогональное проецирование на одну из таких плоскостей будет ортогональным и на остальные плоскости. Очевидно, что ортогональные проекции фигуры на параллельные плоскости равны между собой.
Ортогональное проецирование также имеет только ему присущие свойства. Одно из них выражает теорема о площади ортогональной проекции многоугольника.
Площадь ортогональной проекции
Теорема 5
Площадь ортогональной проекции произвольного многоугольника на плоскость равна произведению площади самого многоугольника на косинус угла между плоскостью многоугольника и плоскостью проекции.
Доказательство:
Как пример многоугольника возьмем 
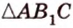
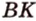
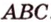
о трех перпендикулярах 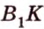
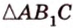
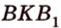
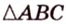
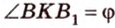
Учитывая, что 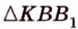
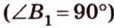
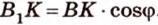
Итак, 
Чтобы доказать теорему для произвольного многоугольника, его разбивают на треугольники. Тогда для каждого треугольника и его проекции можно записать равенство
где 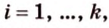
Получим в левой части равенства площадь проекции многоугольника, а в правой — площадь самого многоугольника, умноженную на косинус угла между их плоскостями. Отсюда
Т.е. и для этого случая теорема истинна.
Пример:
Ортогональной проекцией треугольника является треугольник со сторонами 13 см, 14 см и 15 см. Плоскость треугольника образует с плоскостью проекции угол 60°. Вычислите площадь данного треугольника.
Решение:
Воспользуемся рисунком 6.41. Известно, что площадь проекции треугольника вычисляют по формуле:
где 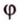
По формуле Герона найдем площадь 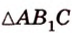
где 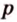
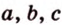
Тогда
Ответ: 168 см2.
- Декартовы координаты на плоскости
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
- Планиметрия — формулы, определение и вычисление
- Параллельность прямых и плоскостей
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
Материал будет полезен для учащихся 10 классов при прохождении темы» Перпендикулярность прямых и плоскостей»
Площадь ортогональной проекции.pptx
Площадь ортогональной проекции
Площадь ортогональной проекции
Геометрия 10 класс
Лапшина И.И.
« Средняя школа №80 с углубленным изучением английского языка»
г. Ярославль
Понятие ортогональной проекции
Понятие ортогональной проекции
А
Чтобы найти ортогональную проекцию
точки на плоскость, надо из этой точки
опустить на плоскость перпендикуляр
О
АО⊥α
α
Основание перпендикуляра О
ортогональная проекция
точки А на плоскость α
Ортогональная проекция треугольника на плоскость
Ортогональная проекция треугольника на плоскость
А
В
С
А 𝟏 А А 𝟏 𝟏𝟏 А 𝟏
В 𝟏 В В 𝟏 𝟏𝟏 В 𝟏
С 𝟏 С С 𝟏 𝟏𝟏 С 𝟏
Если треугольник АВС
параллелен плоскости α,
то его ортогональной
проекцией на плоскость
является треугольник А 1 А А 1 1 А 1 В 1 В В 1 1 В 1 С 1 С С 1 1 С 1
равный данному
α
Ортогональная проекция треугольника на плоскость
Ортогональная проекция треугольника на плоскость
В
С
О
Пусть сторона АВ треугольника
АВС лежит в плоскости α
Тогда ортогональной
проекцией точки С на
плоскость α является точка О.
Т.к. точки А и В лежат в
плоскости α, то их
ортогональной проекцией на
плоскость есть точки А и В
Тогда ⊿АВО-проекция ⊿ АВС на α
Площадь ортогональной проекции многоугольника
Площадь ортогональной проекции многоугольника
В
С
О
Площадь ортогональной
проекции⊿АВО равна
произведению площади ⊿ АВС
на косинус угла между
плоскостью ⊿АВО и плоскостью
⊿АВС
𝑆 ⊿АВО 𝑆𝑆 𝑆 ⊿АВО ⊿АВО 𝑆 ⊿АВО = 𝑆 ⊿АВС 𝑆𝑆 𝑆 ⊿АВС ⊿АВС 𝑆 ⊿АВС ∙𝑐𝑐о𝑠𝑠∠( АВС АВС АВС ; АВО АВО АВО )
Доказательство формулы В С О 𝑆 ⊿АВО 𝑆𝑆 𝑆 ⊿АВО ⊿АВО 𝑆 ⊿АВО = 𝑆 ⊿АВС 𝑆𝑆 𝑆 ⊿АВС ⊿АВС 𝑆 ⊿АВС ∙𝑐𝑐о𝑠𝑠∠(
Доказательство формулы
В
С
О
𝑆 ⊿АВО 𝑆𝑆 𝑆 ⊿АВО ⊿АВО 𝑆 ⊿АВО = 𝑆 ⊿АВС 𝑆𝑆 𝑆 ⊿АВС ⊿АВС 𝑆 ⊿АВС ∙𝑐𝑐о𝑠𝑠∠( АВС АВС АВС ; АВО АВО АВО )
К
Проведем СК ⊥АВ и КО
АВ⊥КО ТТП
СК⊂(АВС)
СО-перпендикуляр
СК-наклонная
КО-проекция
АВ⊂α
Итак: СК⊥АВ
КО⊥АВ
СК⊂(АВС)
КО⊂(АВО)
∠СКО-линейный угол
Доказательство формулы В С О 𝑆 ⊿АВО 𝑆𝑆 𝑆 ⊿АВО ⊿АВО 𝑆 ⊿АВО = 𝑆 ⊿АВС 𝑆𝑆 𝑆 ⊿АВС ⊿АВС 𝑆 ⊿АВС ∙𝑐𝑐о𝑠𝑠∠(
Доказательство формулы
В
С
О
𝑆 ⊿АВО 𝑆𝑆 𝑆 ⊿АВО ⊿АВО 𝑆 ⊿АВО = 𝑆 ⊿АВС 𝑆𝑆 𝑆 ⊿АВС ⊿АВС 𝑆 ⊿АВС ∙𝑐𝑐о𝑠𝑠∠( АВС АВС АВС ; АВО АВО АВО )
К
⊿АВО
𝑆 ⊿АВО 𝑆𝑆 𝑆 ⊿АВО ⊿АВО 𝑆 ⊿АВО = 1 2 1 1 2 2 1 2 АВ∙КО
⊿КСО
КО СК КО КО СК СК КО СК = cos α cos cos α α cos α
КО=СК∙cosα
𝑆 ⊿АВО 𝑆𝑆 𝑆 ⊿АВО ⊿АВО 𝑆 ⊿АВО = 1 2 1 1 2 2 1 2 АВ∙КО= 1 2 1 1 2 2 1 2 АВ∙СКcosα
= 𝑆 АВС 𝑆𝑆 𝑆 АВС АВС 𝑆 АВС ∙cosα
=
Решить №213
Решить №213
Домашнее задание №214
Домашнее задание №214
Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
Введите ваш emailВаш email