В данной публикации мы рассмотрим, как можно найти площадь поверхности цилиндра и разберем примеры решения задач для закрепления материала.
-
Формула вычисления площади цилиндра
- 1. Боковая поверхность
- 2. Основание
- 3. Полная площадь
- Примеры задач
Формула вычисления площади цилиндра
1. Боковая поверхность
Площадь (S) боковой поверхности цилиндра равна произведению длины окружности, являющейся основанием фигуры, на его высоту.
Длина окружности, в свою очередь, рассчитывается так: C = 2 π R. Следовательно, рассчитать площадь можно следующим образом:
S = 2 π R h
Примечание: в вычислениях значение числа π округляется до 3,14.
2. Основание
В качестве оснований цилиндра (равны между собой), выступает круг, площадь которого равна:
S = π R2
Т.к. диаметр круга равен двум его радиусам (d = 2R), выражение можно преобразовать таким образом:
S = π (d/2)2
3. Полная площадь
Для нахождения данной величины необходимо просуммировать площади боковой поверхности и двух равных оснований цилиндра, т.е.:
S = 2 π R h + 2 π R2 или S = 2 π R (h + R)
Примеры задач
Задание 1
Найдите площадь боковой поверхности цилиндра, если его радиус равен 11 см, а высота – 8 см.
Решение:
Воспользуемся первой формулой, подставив в нее данные по условиям задачи значения:
S = 2 ⋅ 3,14 ⋅ 11 см ⋅ 8 см = 552,64 см2.
Задание 2
Высота цилиндра равна 9 см, а его диаметр – 8 см. Найдите суммарную площадь поверхности фигуры.
Решение:
Если диаметр цилиндра равен 8 см, значит его радиус составляет 4 см (8 см / 2). Применив соответствующую формулу для нахождения площади получаем:
S = 2 ⋅ 3,14 ⋅ 4 см ⋅ (9 см + 4 см) = 326,56 см2.
10
Сен 2013
Категория: 02 Стереометрия
02. Цилиндр.
2013-09-10
2022-09-11
Задача 1. Радиус основания цилиндра равен высота равна
Найдите площадь боковой поверхности цилиндра, деленную на
.
Решение: + показать
Задача 2. Площадь боковой поверхности цилиндра равна а диаметр основания равен
Найдите высоту цилиндра.
Решение: + показать
Задача 3. Длина окружности основания цилиндра равна высота равна
Найдите площадь боковой поверхности цилиндра.
Решение: + показать
Задача 4. Площадь осевого сечения цилиндра равна Найдите площадь боковой поверхности цилиндра, деленную на
.
Решение: + показать
Задача 5. Объём первого цилиндра равен 48 м У второго цилиндра высота в три раза больше, а радиус основания в два раза меньше, чем у первого. Найдите объём второго цилиндра (в м
).
Решение: + показать
Задача 6. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.
Решение: + показать
Задача 7. В цилиндрический сосуд налили см
воды. Уровень воды при этом достигает высоты
см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на
см. Чему равен объем детали? Ответ выразите в см
Решение: + показать
Задача 8. В цилиндрический сосуд налили см
воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в
раза. Найдите объем детали.
Ответ выразите в см
Решение: + показать
Задача 9. В цилиндрическом сосуде уровень жидкости достигает см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в
раза больше первого? Ответ выразите в сантиметрах.
Решение: + показать
Задача 10. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 11. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 12. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Задача 13. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите
.
Решение: + показать
Вы можете пройти тест “Цилиндр”
Автор: egeMax |
комментария 3
Печать страницы
Как найти площадь основания цилиндра
Если в условиях задачи не уточняется, о каком именно цилиндре идет речь (параболический, эллиптический, гиперболический и т.д.), то подразумевается самый простой вариант. У такой пространственной геометрической фигуры в основаниях лежат круги, а боковая поверхность образует с ними прямой угол. Вычисление параметров в этом случае не представляет особой сложности.

Инструкция
Если известен радиус (r) основания цилиндра, то все остальные его размеры не имеют значения при расчетах. Вычислите произведение числа Пи, округленного до нужной степени точности, на возведенный в квадрат радиус — это и будет площадь основания цилиндра (S): S=π*r². Например, если диаметр (это, как вы знаете, удвоенный радиус) цилиндра равен 70см, а результат вычисления требуется получить с точностью до второго знака после запятой (сотых долей сантиметра), то площадь основания составит 3,14*(70/2)² = 3,14*35² = 3,14*1225 ≈ 3848,45см².
Если радиус и диаметр неизвестны, но даны высота (h) и объем (V) цилиндра, то этих параметров тоже будет достаточно для нахождения площади (S) основания фигуры — просто разделите объем на высоту: S=V/h. Например, при объеме равном 950см³ и высоте в 20см цилиндр будет иметь основание площадью в 950/20=47,5см².
Если кроме высоты (h) цилиндра известна площадь его боковой поверхности (p), то для нахождения площади основания (S) возведите площадь боковой поверхности в квадрат и разделите результат на учетверенное произведение числа Пи на возведенную в квадрат высоту: S=p²/(4*π*h²). Например, если площадь боковой поверхности равна 570см², то при высоте цилиндра в 25см и заданной точности расчетов в одну сотую сантиметра он должен иметь площадь основания, равную 570²/(4*3,14*25²) = 324900/(12,56*625) = 324900/7850 ≈ 41,39см².
Если кроме площади боковой поверхности цилиндра (p) известна и площадь всей поверхности (P), то, отняв от второго первое, не забудьте разделить полученный результат пополам, так как общая площадь включает оба основания цилиндра: S=(P-p)/2. Например, если общая площадь пространственной фигуры составляет 980см², а площадь ее боковой поверхности — 750см², то площадь каждого из оснований будет равна (980-750)/2=115см².
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Содержание
Введение
1 Теоретическая часть
1.1. Определение
цилиндра
1.2. Элементы и
свойства цилиндра
1. 3. Сечения
цилиндра
1.4. Площадь
цилиндра
1.5. Объем цилиндра
2 Практическая часть (задачи)
Задача 1.
Задача 2.
Задача 3.
Задача 4.
Задача 5.
Задача 6.
Задача 7.
Задача 8.
Задача 9.
Задача 10.
Задача 11.
Задача 12.
Заключение
Список литературы
Введение
Стереометрия −
это раздел геометрии, в котором изучаются фигуры в пространстве. Основными
фигурами в пространстве являются точка, прямая и плоскость. В стереометрии
появляется новый вид взаимного расположения прямых: скрещивающиеся прямые. Это
одно из немногих существенных отличий стереометрии от планиметрии, так как во
многих случаях задачи по стереометрии решаются путем рассмотрения различных
плоскостей, в которых выполняются планиметрические законы.
В окружающей нас
природе существует множество объектов, являющихся физическими моделями
указанной фигуры. Например, многие детали машин имеют форму цилиндра или
представляют собой некоторое их сочетание, а величественные колонны храмов и
соборов, выполненные в форме цилиндров, подчеркивают их гармонию и красоту.
Греч. − кюлиндрос.
Античный термин. В обиходе − свиток папируса, валик, каток (глагол − крутить,
катать).
У Евклида цилиндр
получается вращением прямоугольника. У Кавальери − движением образующей (при
произвольной направляющей − «цилиндрика»).
Цель данного
реферата рассмотреть геометрическое тело – цилиндр.
Для достижения
данной цели необходимо рассмотреть следующие задачи:
− дать
определения цилиндра;
− рассмотреть
элементы цилиндра;
− изучить
свойства цилиндра;
− рассмотреть
виды сечения цилиндра;
− вывести формулу
площади цилиндра;
− вывести формулу
объема цилиндра;
− решить задачи с
использованием цилиндра.
1 Теоретическая часть
1.1. Определение цилиндра
Рассмотрим
какую-либо линию (кривую, ломаную или смешанную) l, лежащую в некоторой плоскости
α, и некоторую прямую S, пересекающую эту плоскость. Через все точки данной
линии l проведем прямые, параллельные прямой S; образованная этими прямыми
поверхность α называется цилиндрической поверхностью. Линия l называется
направляющей этой поверхности, прямые s1, s2, s3,…
− ее образующими.
Если направляющая
является ломаной, то такая цилиндрическая поверхность состоит из ряда плоских
полос, заключенных между парами параллельных прямых, и называется
призматической поверхностью. Образующие, проходящие через вершины направляющей
ломаной, называются ребрами призматической поверхности, плоские полосы между
ними − ее гранями.
Если рассечь
любую цилиндрическую поверхность произвольной плоскостью, не параллельной ее
образующим, то получим линию, которая также может быть принята за направляющую
данной поверхности. Среди направляющих выделяется та, которая, получается, от
сечения поверхности плоскостью, перпендикулярной образующим поверхности. Такое
сечение называется нормальным сечением, а соответствующая направляющая −
нормальной направляющей.
Если направляющая
− замкнутая (выпуклая) линия (ломаная или кривая), то соответствующая поверхность
называется замкнутой (выпуклой) призматической или цилиндрической поверхностью.
Из цилиндрических поверхностей простейшая имеет своей нормальной направляющей
окружность. Рассечем замкнутую выпуклую призматическую поверхность двумя
плоскостями, параллельными между собой, но не параллельными образующим.
В сечениях
получим выпуклые многоугольники. Теперь часть призматической поверхности,
заключенная между плоскостями α и α’, и две образовавшиеся при этом
многоугольные пластинки в этих плоскостях ограничивают тело, называемое
призматическим телом − призмой.
Цилиндрическое
тело − цилиндр определяется аналогично призме:
Цилиндром называется тело, ограниченное с боков замкнутой (выпуклой)
цилиндрической поверхностью, а с торцов двумя плоскими параллельными
основаниями. Оба основания цилиндра равны, также равны между собой и все
образующие цилиндра, т.е. отрезки образующих цилиндрической поверхности между
плоскостями оснований.
Цилиндром
(точнее, круговым цилиндром) называется геометрическое тело, которое состоит
из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным
переносом, и всех отрезков, соединяющих соответствующие точки этих кругов (рис.
1).
Рис. 1 − Цилиндр
1.2. Элементы и свойства цилиндра
Круги называются
основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей
кругов, − образующими цилиндра.
Так как
параллельный перенос есть движение, то основания цилиндра равны.
Так как при параллельном
переносе плоскость переходит в параллельную плоскость (или в себя), то у
цилиндра основания лежат в параллельных плоскостях.
Так как при
параллельном переносе точки смещаются по параллельным (или совпадающим) прямым
на одно и то же расстояние, то у цилиндра образующие параллельны и равны.
Поверхность
цилиндра состоит из оснований и боковой поверхности. Боковая поверхность
составлена из образующих.
Цилиндр
называется прямым, если его образующие перпендикулярны плоскостям оснований.
Прямой цилиндр
наглядно можно представить себе как геометрическое тело, которое описывает
прямоугольник при вращении его около стороны как оси (рис. 2).
Рис. 2 − Прямой
цилиндр
В дальнейшем мы
будем рассматривать только прямой цилиндр, называя его для краткости просто
цилиндром.
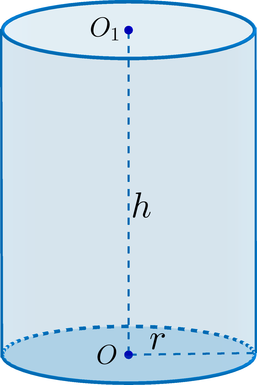
Радиусом цилиндра
называется радиус его основания. Высотой цилиндра называется расстояние между
плоскостями его оснований. Осью цилиндра называется прямая, проходящая через
центры оснований. Она параллельна образующим.
Цилиндр
называется равносторонним, если
его высота равна диаметру основания.
Если основания
цилиндра плоские (и, следовательно, содержащие их плоскости параллельны), то
цилиндр называют стоящим на плоскости. Если основания стоящего на плоскости
цилиндра перпендикулярны образующей, то цилиндр называется прямым.
В частности, если
основание стоящего на плоскости цилиндра − круг, то говорят о круговом
(круглом) цилиндре; если эллипс − то эллиптическом.
1. 3. Сечения цилиндра
Сечение цилиндра
плоскостью, параллельной его оси, представляет собой прямоугольник. Две его
стороны − образующие цилиндра, а две другие − параллельные хорды оснований.
В частности,
прямоугольником является осевое сечение. Это − сечение цилиндра плоскостью,
проходящей через его ось.
Сечение цилиндра
плоскостью, параллельной основанию − круг .
Теорема 1.
Плоскость, параллельная плоскости основания цилиндра, пересекает его боковую
поверхность по окружности, равной окружности основания.

Пусть β − плоскость, параллельная плоскости основания цилиндра. Параллельный
перенос в направлении оси цилиндра, совмещающий плоскость β с плоскостью
основания цилиндра, совмещает сечение боковой поверхности плоскостью β с
окружностью основания. Теорема доказана.
1.4. Площадь цилиндра
Площадь
боковой поверхности цилиндра.
За площадь
боковой поверхности цилиндра принимается предел, к которому стремится площадь
боковой поверхности правильной призмы, вписанной в цилиндр, когда число сторон
основания этой призмы неограниченно возрастет.
Теорема 2.
Площадь боковой поверхности цилиндра равна произведению длины окружности его
основания на высоту (Sбок.ц = 2πRH, где R − радиус основания
цилиндра, Н − высота цилиндра).
а) 
Рис. 4 − Площадь
боковой поверхности цилиндра
Доказательство.
Пусть Pn и Н соответственно периметр основания
и высота правильной n-угольной призмы, вписанной в цилиндр (рис. 4, а). Тогда
площадь боковой поверхности этой призмы Sбок.ц − PnH. Предположим, что число сторон
многоугольника, вписанного в основание, неограниченно растет (рис. 4, б). Тогда
периметр Pn стремится к длине окружности С =
2πR, где R— радиус основания цилиндра, а высота H не изменяется. Таким образом,
площадь боковой поверхности призмы стремится к пределу 2πRH, т.
е. площадь боковой поверхности
цилиндра равна Sбок.ц = 2πRH. Теорема доказана.
Площадь полной
поверхности цилиндра.
Площадью полной
поверхности цилиндра называется сумма площадей боковой поверхности и двух
оснований. Площадь каждого основания цилиндра равна πR2,
следовательно, площадь полной поверхности
цилиндра Sполн вычисляется
по формуле Sбок.ц = 2πRH+ 2πR2.
Рис. 5 − Площадь
полной поверхности цилиндра
Если боковую
поверхность цилиндра разрезать по образующей АT, и развернуть так, чтобы все
образующие оказались в одной плоскости, то в результате мы получим
прямоугольник АTT1А1, который называется разверткой боковой поверхности
цилиндра. Сторона FF1 прямоугольника есть развертка окружности основания
цилиндра, следовательно, АА1=2πR, а его сторона АT равна образующей цилиндра,
т. е. АT = Н (рис. 5, б). Таким образом, площадь АT∙АА1=2πRH развертки цилиндра
равна площади его боковой поверхности.
1.5. Объем цилиндра
Если
геометрическое тело простое, то есть допускает разбиение на конечное число
треугольных пирамид, то его объем равен сумме объемов этих пирамид. Для
произвольного тела объем определяется следующим образом.
Данное тело имеет
объем V, если существует содержащие его простые тела и содержащиеся в нем
простые тела с объемами, сколько угодно мало отличающимися от V.
Применим это
определение к нахождению объема цилиндра с радиусом основания R и высотой Н.
При выводе
формулы для площади круга были построены такие два n-угольника (один −
содержащий круг, другой − содержащийся в круге), что их площади при
неограниченном увеличении n неограниченно приближались к площади круга.
Построим такие многоугольники для круга в основании цилиндра. Пусть Р −
многоугольник, содержащий круг, а Р’ − многоугольник, содержащийся в круге
(рис. 6).
Рис. 7 − Цилиндр
с описанной и вписанной в него призмой
Построим две
прямые призмы с основаниями Р и Р’ и высотой Н, равной высоте цилиндра. Первая
призма содержит цилиндр, а вторая призма содержится в цилиндре. Так как при
неограниченном увеличении n площади оснований призм неограниченно приближаются
к площади основания цилиндра S, то их объемы неограниченно приближаются к SН.
Согласно определению объем цилиндра
V = SH = πR2H.
Итак, объем
цилиндра равен произведению площади основания на высоту.
2 Практическая часть (задачи)
Задача 1.
Осевое сечение
цилиндра − квадрат, площадь которого Q.
Найдите площадь
основания цилиндра.
Дано: цилиндр,
квадрат − осевое сечение цилиндра, Sквадрата = Q.
Найти: Sосн.цил.
Решение:
Сторона квадрата
равна . Она равна диаметру
основания. Поэтому площадь основания равна 
Ответ: Sосн.цил. =
Задача 2.
В цилиндр вписана
правильная шестиугольная призма. Найдите угол между диагональю ее боковой грани
и осью цилиндра, если радиус основания равен высоте цилиндра.
Дано: цилиндр,
правильная шестиугольная призма вписанная в цилиндр, радиус основания = высоте
цилиндра.
Найти: угол между
диагональю ее боковой грани и осью цилиндра.
Решение: Боковые
грани призмы − квадраты, так как сторона правильного шестиугольника, вписанного
в окружность, равна радиусу.
Ребра призмы
параллельны оси цилиндра, поэтому угол между диагональю грани и осью цилиндра
равен углу между диагональю и боковым ребром. А это угол равен 45°, так как грани
− квадраты.
Ответ: угол между
диагональю ее боковой грани и осью цилиндра = 45°.
Задача 3.
Высота цилиндра
6см, радиус основания 5см.
Найдите площадь
сечения, проведенного параллельно оси цилиндра на расстоянии 4см от нее.
Дано: Н = 6см, R
= 5см, ОЕ = 4см.
Найти: Sсеч.
Решение:
Sсеч.= КМ×КС,
ОЕ = 4
см, КС = 6 см.
Треугольник ОКМ −
равнобедренный (ОК = ОМ = R = 5 см),
треугольник ОЕК −
прямоугольный.
Из треугольника
ОЕК, по теореме Пифагора:
ЕК = ,
КМ = 2ЕК = 2×3 = 6,
Sсеч.= 6×6 = 36 см2.
Ответ: Sсеч.= 36 см2.
Задача 4.
Высота цилиндра
12см, радиус основания 10см.
Цилиндр пересечен
плоскостью так, что в сечении получился квадрат.
Найдите
расстояние от этого сечения до оси.
Дано: СК = h =
12см, R = ОК = ОМ = 10см.
Найти: ОЕ.
 |
Решение:
СК равна высоте,
то есть СК = 12 см. Так как в сечении получился квадрат, то КМ = СК = 12см.
ОК − радиус
основания, ОК = 10см.
Треугольник ОКЕ –
прямоугольный, где ОК = 10см, КЕ = 6см.
По теореме
Пифагора:
ОЕ =
Ответ: ОЕ = 8см.
Задача 5.
В цилиндр наклонно
вписан квадрат так, что все его вершины лежат на окружностях основания. Найдите
сторону квадрата, если высота цилиндра равна 2см, а радиус основания равен 7см.
Дано: цилиндр, h = 2см, R – 7см, АВСD − наклонно вписанный
квадрат.
Найти: АВ.
 |
|||
Решение:
Достроим квадрат
АВСD до прямого прямоугольного параллелограмма АВС1D1А1В1СD
с диагональным сечением АВСD.
Угол АВС1
= 90°. Так как вписанный в окружность угол, стороны которого проходят через две
данные точки окружности, равен половине угла между радиусами, проходившими в
эти точки, или дополняет половину этого угла до 180°, то АС1 есть
диаметр окружности верхнего основания цилиндра.
Рассмотрим
прямоугольный треугольник СС1А1 − катет СС1,
есть образующая цилиндра и СС1 = 2АС, катет АС1 есть
диаметр цилиндра и АС1 = 14. По теореме Пифагора АС = (см).
Из прямоугольного
равнобедренного треугольника АВС по теореме Пифагора сторона квадрата АВ = 
Ответ: АВ = 10
см.
Задача 6.
Объем цилиндра
120 см2, его высота 3,6 см.
Найти радиус
цилиндра.
Дано: V = 120 см2,
h = 3,6 см.
Найти: r
Решение:
Ответ: r = 3,3.
Задача 7.
Осевым сечением
цилиндра является квадрат, диагональ которого равна см.
Найдите площадь
поверхности цилиндра.
Дано: цилиндр, АВСD − осевое сечение, АВ =
АD, ВD = см.
Найти: Sпов.цил.
Решение:
Из прямоугольного
∆ АВD по теореме Пифагора: ВD2 − 2AB2, откуда сторона квадрата АВ 
см, радиус цилиндра ОА − 1,5 см.
Площадь боковой
поверхности Sбок.ц
= 2πRH = 2π×1,5×3 = 9π (см2).
Площадь основания
Sосн. = 2πR2 = 2π×1,52 = 4,5π (см2).
Площадь полной
поверхности Sпов.цил.
= Sбок.ц
+ Sосн. = 9π + 4,5π = 13,5 π (см2).
Ответ: 13,5 π (см2).
Задача 8.
В цилиндр вписана
правильная шестиугольная призма.
Найдите отношения
объема призмы к объему цилиндра.
Дано: цилиндр,
правильная шестиугольная призма вписана в цилиндр, а − сторона призмы.
Найти: 
Решение:

а6 = R
Ответ: 
.
Задача 9.
Диаметр основания
цилиндра 1м.
Найдите площадь
боковой поверхности цилиндра.
Дано: цилиндр, d
= АВ = 1м.
Найти: Sбок.ц.
Решение:
Sбок. = 2πRh,
R = = 0,5 м,
Sбок. = 2πR × 2πR = (2πR)2 = 4π2 ×0,25
= π2
Ответ: Sбок. = π2 (м2).
Задача 10.
Найдите радиус
основания цилиндра наибольшего объема, вписанного в конус, радиус основания
которого равен 3.
Дано: конус,
цилиндр – вписан в конус, ОВ – радиус конуса, ОВ = 3.
Найти: r − радиус основания цилиндра.
Решение:
Обозначим через h
и r высоту и радиус основания цилиндра, вписанного в конус с вершиной A.
Рассмотрим осевое сечение конуса – равнобедренный треугольник ABC с высотой AO
= H и основанием BC = 2· 3 = 6 (рис.2). Плоскость ABC пересекает цилиндр,
вписанный в конус, по его осевому сечению – прямоугольнику KLMN, где точки K и
L лежат соответственно на отрезках AB и AC, а точки M и N – на отрезке BC ,
причём KL = 2r , KN = LM = h . Пусть P – точка пересечения AO и KL . Треугольник
APL подобен треугольнику AOC , поэтому
, или
откуда 

Найдем наибольшее значение функции V(r) на
промежутке (0;3) .
V’(r) = H(2r — r2) = Hr(2 — r).
Промежутку (0;3) принадлежит единственный
корень ( r = 2 ) полученного уравнения. Если 0 < r < 2 , то V'(r) > 0 .
Поэтому на промежутке (0;2) функция V(r) возрастает. Если 2 < r < 3 , то V'(r)
< 0 . Поэтому на промежутке (2;3) функция V(r) убывает. Значит, в точке r = 2
функция V(r) имеет максимум. Следовательно, радиус основания цилиндра
наибольшего объема, вписанного в данный конус, равен 2.
Ответ: r = 2.
Задача 11.
Развертка боковой
поверхности цилиндра есть квадрат со стороной . Найдите объем цилиндра.
Дано: Цилиндр,
квадрат – развертка боковой поверхности цилиндра, сторона квадрата = .
Найти: Vцил.
Решение:
Пусть образующая
цилиндра АD = h , а радиус основания равен r, объем цилиндра равен V .
Поскольку развертка боковой поверхности цилиндра есть квадрат со стороной длина
окружности основания и образующая цилиндра также равны , т.е.
.
Следовательно, 
Ответ: V = 2.
Задача 12.
Радиус основания
цилиндра равен r . Плоскость пересекает боковую поверхность цилиндра, не
пересекает его оснований и образует угол α с плоскостью основания. Найдите
площадь сечения цилиндра этой плоскостью.
Дано: цилиндр, r
– радиус основания цилиндра, угол α.
Найти: Sсеч.ц.
Основание
цилиндра есть ортогональная проекция данного сечения на плоскость основания.
Следовательно, площадь сечения равна площади основания, делённой на косинус
угла между плоскостями сечения и основания, т.е. .
Ответ:
Заключение
Цель данного
реферата выполнена, рассмотрено такое геометрическое тело, как цилиндр.
Рассмотрены
следующие задачи:
− дано
определение цилиндра;
− рассмотрены
элементы цилиндра;
− изучены
свойства цилиндра;
− рассмотрены
виды сечения цилиндра;
− выведена
формула площади цилиндра;
− выведена
формула объема цилиндра;
− решены задачи с
использованием цилиндра.
Список литературы
1. Погорелов А. В. Геометрия:
Учебник для 10 – 11 классов общеобразовательных учреждений, 1995.
2. Бескин Л.Н. Стереометрия.
Пособие для учителей средней школы, 1999.
3. Атанасян Л. С., Бутузов В.
Ф., Кадомцев С. Б., Киселева Л. С., Позняк Э. Г. Геометрия: Учебник для 10 – 11
классов общеобразовательных учреждений, 2000.
4. Александров А.Д., Вернер
А.Л., Рыжик В.И. Геометрия: учебник для 10-11 классов общеобразовательных
учреждений, 1998.
5. Киселев А. П., Рыбкин Н. А.
Геометрия: Стереометрия: 10 – 11 классы: Учебник и задачник, 2000.
8. Геометрия в пространстве (стереометрия)
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на тему «Цилиндр»
Прямой цилиндр:
(blacktriangleright) Ось цилиндра – прямая, соединяющая центры его оснований.
Отрезок, соединяющий центры оснований – высота.
(blacktriangleright) Образующая цилиндра – перпендикуляр, проведенный из точки границы одного основания к другому основанию.
Заметим, что образующая и высота цилиндра равны друг другу.
(blacktriangleright) Площадь боковой поверхности цилиндра ({Large{S_{text{бок.пов.}}=2pi rh}}), где (r) – радиус основания, (h) – высота (или образующая).
(blacktriangleright) Площадь полной поверхности цилиндра равна сумме площади боковой поверхности и площадей оснований. [{Large{S_{text{полн.пов.}}=2pi rh+2pi r^2}}]
(blacktriangleright) Объем цилиндра ({Large{V=S_{text{осн}}cdot
h=pi r^2h}})
Заметим, что прямой цилиндр имеет некоторое сходство с прямой призмой, только в ее основаниях лежат многоугольники (граница которых – ломаная), а в основаниях цилиндра – круги (граница которых гладкая).
Поэтому можно сказать, что боковая поверхность прямой призмы “ребристая”, а цилиндра – “гладкая”.
Задание
1
#2743
Уровень задания: Равен ЕГЭ
Про прямые круговые цилиндры (C_1) и (C_2) известно, что у (C_1) радиус основания в два раза больше, чем у (C_2), но у (C_2) высота в три раза больше, чем у (C_1). Найдите отношение объёма цилиндра (C_2) к объёму (C_1).
Обозначим высоту цилиндра (C_1) через (h_1), а высоту цилиндра (C_2) через (h_2). Обозначим радиус основания цилиндра (C_1) через (r_1), а радиус основания цилиндра (C_2) через (r_2). Тогда [r_1 = 2r_2,qquad h_2 = 3h_1,.]
Объём цилиндра (C_1) равен (pi {r_1}^2 h_1 = 4pi {r_2}^2 h_1), а объём цилиндра (C_2) равен (3pi {r_2}^2 h_1), тогда [dfrac{V_{C_2}}{V_{C_1}} = dfrac{3pi {r_2}^2 h_1}{4pi {r_2}^2 h_1} = 0,75]
Ответ: 0,75
Задание
2
#1861
Уровень задания: Равен ЕГЭ
Объем цилиндра равен (64pi), а площадь боковой поверхности равна (32pi). Найдите площадь полной поверхности цилиндра, деленную на (pi).
Формулы для нахождения объема и боковой поверхности цилиндра: (V = pi R^2 h), (S_{text{бок}} = 2pi R h). Зная величину объема и боковой поверхности, можно выразить радиус цилиндра: [frac{V}{S_{text{бок}}} = frac{pi R^2 h}{2pi R h} = frac{R}{2} = frac{64pi}{32pi} = 2] (Rightarrow) (R = 4). Площадь полной поверхности складывается из площади боковой поверхности и площадей двух оснований: [S_{text{полн}} = 2pi R h + 2 pi R^2 = 32pi + 2 cdot 16pi = 64pi.] Осталось разделить полученный объем на (pi), тогда окончательно получаем (64).
Ответ: 64
Задание
3
#1862
Уровень задания: Равен ЕГЭ
Объем цилиндра равен (100pi), а площадь боковой поверхности равна (25pi). Найдите высоту цилиндра.
Формулы для нахождения объема и боковой поверхности цилиндра: (V = pi R^2 h), (S_{text{бок}} = 2pi R h). Зная величину объема и боковой поверхности, можно выразить радиус цилиндра: [frac{V}{S_{text{бок}}} = frac{pi R^2 h}{2pi R h} = frac{R}{2} = frac{100pi}{25pi} = 4] (Rightarrow) (R = 
Ответ: 1,5625
Задание
4
#953
Уровень задания: Равен ЕГЭ
Объём цилиндра [V = dfrac{200}{sqrt{pi}},] а отношение радиуса его основания к его высоте равно (5). Найдите площадь полной поверхности этого цилиндра.
[V_{text{цил}} = pi R^2 H = dfrac{200}{sqrt{pi}},] (dfrac{R}{H} = 5), где (R) – радиус основания цилиндра, (H) – его высота, тогда (R = 5H), следовательно, [pi cdot 25 H^3 = dfrac{200}{sqrt{pi}}qquadRightarrowqquad H^3 = dfrac{8}{pisqrt{pi}},] откуда (H = dfrac{2}{sqrt{pi}}), (R = dfrac{10}{sqrt{pi}}). [S_{text{полн}} = 2pi R H + pi R^2 = 2pi R(H + R) = 2picdotdfrac{10}{sqrt{pi}}cdotdfrac{12}{sqrt{pi}} = 240.]
Ответ: 240
Задание
5
#952
Уровень задания: Сложнее ЕГЭ
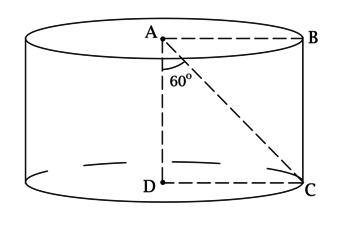
(AD) – ось цилиндра, (BC) – его образующая, (S_{ABCD} = dfrac{16sqrt{3}}{sqrt[3]{pi^2}}), (angle CAD = 60^circ). Найдите объём цилиндра.
Так как (AD) и (BC) – высоты цилиндра, то (ABCD) – прямоугольник, тогда [S_{ABCD} = ADcdot DC = Hcdot R = dfrac{16sqrt{3}}{sqrt[3]{pi^2}}.]
Рассмотрим прямоугольный треугольник (ADC):
Т.к. (angle DAC = 60^circ), то [AD = mathrm{tg}, angle ACDcdot DC = mathrm{tg}, 30^circcdot R = dfrac{R}{sqrt{3}},] т.е. (H = dfrac{R}{sqrt{3}}) или (R = sqrt{3}H).
Подставляя выражение для (R) в (S_{ABCD}), получим: [H^2cdotsqrt{3} = dfrac{16sqrt{3}}{sqrt[3]{pi^2}},] откуда (H = dfrac{4}{sqrt[3]{pi}}), тогда (R = dfrac{4sqrt{3}}{sqrt[3]{pi}}).
[V_{text{цил}} = pi R^2 H = picdot dfrac{16cdot 3}{sqrt[3]{pi^2}}cdotdfrac{4}{sqrt[3]{pi}} = 192.]
Ответ: 192
Повторение базовой теории и формул, в том числе и тех, которые позволяют выполнить расчет объема цилиндра, — один из основных этапов подготовки к ЕГЭ. Несмотря на то, что эта тема достаточно подробно рассматривается на уроках математики в школе, с необходимостью вспомнить основной материал и «прокачать» навык решения задач сталкиваются многие учащиеся. Понимая, как вычислить объем и другие неизвестные параметры цилиндра, старшеклассники смогут получить достаточно высокие баллы по итогам сдачи единого государственного экзамена.
Основные нюансы, которые стоит вспомнить
Чтобы вопрос, как посчитать объем цилиндра и выполнить измерение других неизвестных параметров при решении задач, не ставил ученика в тупик, рекомендуем повторить основные свойства этой фигуры прямо сейчас в режиме онлайн.
Важно помнить, что:
- Цилиндр представляет собой тело, которое ограничено цилиндрической поверхностью и двумя кругами. Цилиндрическая поверхность является боковой. А круги представляют собой основания фигуры.
- Высота цилиндра есть расстояние между плоскостями его оснований.
- Все его образующие являются параллельными и равными между собой.
- Радиус цилиндра есть радиус его основания.
- Фигура называется прямой, если ее образующие перпендикулярны основаниям.
Как подготовиться к экзамену качественно и эффективно?
Занимаясь накануне прохождения аттестационного испытания, многие учащиеся сталкиваются с проблемой поиска необходимой информации. Далеко не всегда школьный учебник оказывается под рукой, когда это требуется. А найти формулы, которые помогут рассчитать площадь и другие неизвестные параметры цилиндра, часто бывает достаточно сложно даже в Интернете в онлайн-режиме.
Занимаясь вместе с математическим порталом «Школково», выпускники смогут избежать типовых ошибок и успешно сдать единый госэкзамен. Мы предлагаем выстроить процесс подготовки по-новому, переходя от простого к сложному. Это позволит учащимся определить непонятные для себя тематики и ликвидировать пробелы в знаниях.
Весь базовый материал, который поможет в решении задач на тему «Цилиндр», выпускники смогут найти в разделе «Теоретическая справка». Специалисты «Школково» изложили с доступной форме все необходимые определения и формулы.
Для закрепления полученных знаний учащиеся могут попрактиковаться в решении задач на тему «Цилиндр» и другие темы, например, нахождение площади или объема конуса. Большая, постоянно обновляющаяся подборка заданий представлена в разделе «Каталог».
Чтобы во время подготовки к ЕГЭ быстро найти конкретную задачу по теме «Цилиндр» и освежить в памяти алгоритм ее решения, выпускники могут предварительно сохранить ее в «Избранное». Отрабатывать собственные навыки на нашем сайте имеют возможность не только столичные школьники, но и учащиеся из других российских городов.

УСТАЛ? Просто отдохни