Как найти площадь основания круга конуса

Как найти площадь основания конуса формула. Площадь боковой и полной поверхности конуса

Площадь поверхности конуса (или просто поверхность конуса) равна сумме площадей основания и боковой поверхности.

Площадь боковой поверхности конуса вычисляется по формуле: S = πRl
, где R — радиус основания конуса, а l
— образующая конуса.

Так как площадь основания конуса равна πR 2 (как площадь круга), то площадь полной поверхности конуса будет равна: πR 2 + πRl
= πR (R + l
).

Получение формулы площади боковой поверхности конуса можно пояснить такими рассуждениями. Пусть на чертеже изображена развёртка боковой поверхности конуса. Разделим дугу АВ на возможно большее число равных частей и все точки деления соединим с центром дуги, а соседние — друг с другом хордами.

Получим ряд равных треугольников. Площадь каждого треугольника равна ah
/
2 , где а
— длина основания треугольника, a h
— его высота.

Сумма площадей всех треугольников составит: ah
/
2 n
= anh

/
2 , где n
— число треугольников.

При большом числе делений сумма площадей треугольников становится весьма близкой к площади развёртки, т. е. площади боковой поверхности конуса. Сумма оснований треугольников, т. е. an
, становится весьма близкой к длине дуги АВ, т. е. к длине окружности основания конуса. Высота каждого треугольника становится весьма близкой к радиусу дуги, т. е. к образующей конуса.

Пренебрегая незначительными различиями в размерах этих величин, получаем формулу площади боковой поверхности конуса (S):

S = Cl
/
2 , где С — длина окружности основания конуса, l
— образующая конуса.

Зная, что С = 2πR, где R — радиус окружности основания конуса, получаем: S = πRl
.

Примечание.
В формуле S = Cl
/
2 поставлен знак точного, а не приближённого равенства, хотя на основании проведённого рассуждения мы могли бы это равенство считать приближённым. Но в старших классах средней школы доказывается, что равенство

S = Cl
/
2 точное, а не приближённое.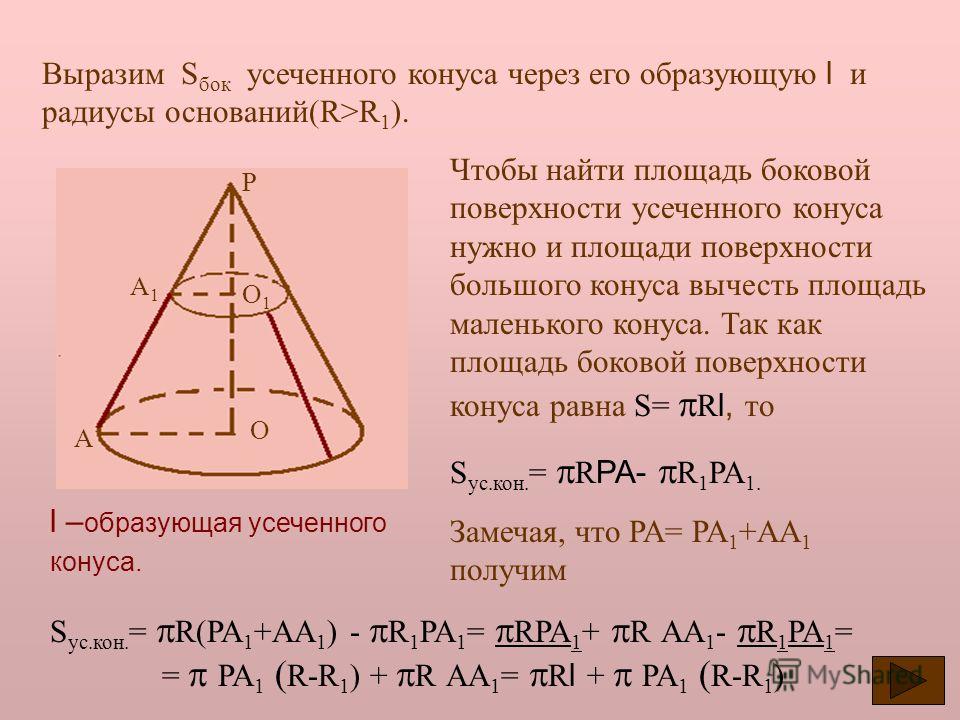

Теорема.
Боковая поверхность конуса равна произведению длины окружности основания на половину образующей.

Впишем в конус (рис.) какую-нибудь правильную пирамиду и обозначим буквами р
и l
числа, выражающие длины периметра основания и апофемы этой пирамиды.

Тогда боковая поверхность её выразится произведением 1 / 2 р
l
.

Предположим теперь, что число сторон вписанного в основание многоугольника неограниченно возрастает. Тогда периметр р
будет стремиться к пределу, принимаемому за длину С окружности основания, а апофема l
будет иметь пределом образующую конуса (так как из ΔSAK следует, что SA — SK

1 / 2 р
l
, будет стремиться к пределу 1 / 2 С
L. Этот предел и принимается за величину боковой поверхности конуса. Обозначив боковую поверхность конуса буквой S, можем написать:

S = 1 / 2 С
L = С
1 / 2 L

Следствия.

1) Так как С = 2π
R, то боковая поверхность конуса выразится формулой:

S = 1 / 2
2π
R
L = π
RL

2) Полную поверхность конуса получим, если боковую поверхность сложим с площадью основания; поэтому, обозначая полную поверхность через Т, будем иметь:

T = π
RL + π
R 2 = π
R(L + R)

Теорема.
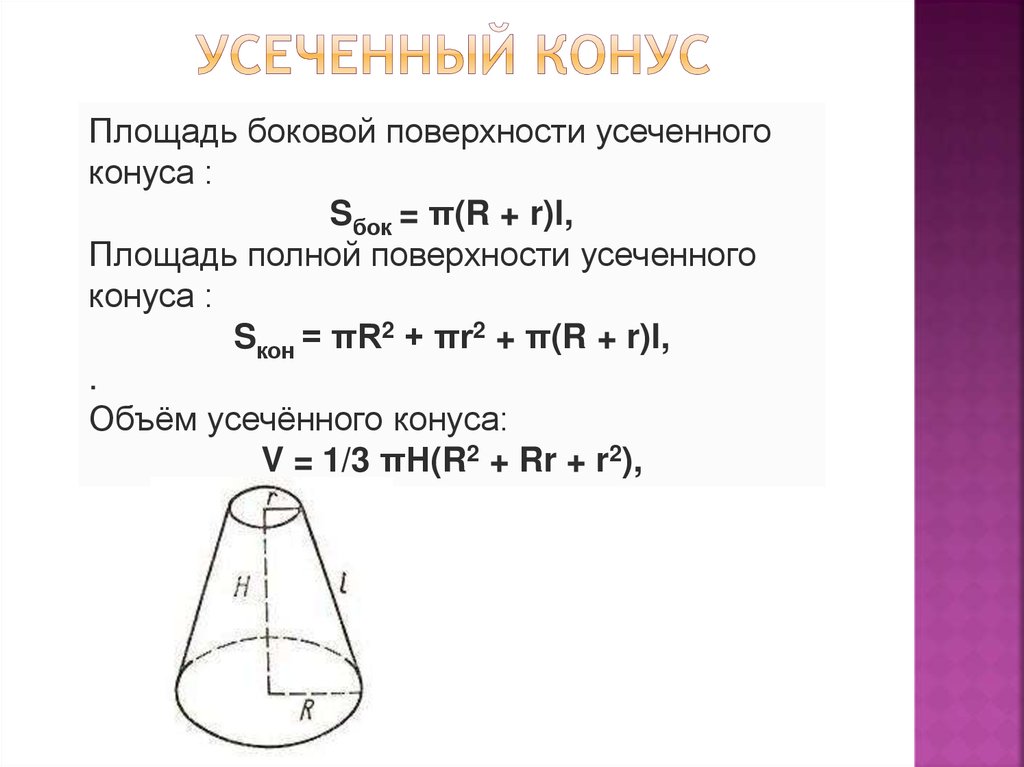
Боковая поверхность усечённого конуса равна произведению полусуммы длин окружностей оснований на образующую.

Впишем в усечённый конус (рис.) какую-нибудь правильную усечённую пирамиду и обозначим буквами р, р
1 и l
числа, выражающие в одинаковых линейных единицах длины периметров нижнего и верхнего оснований и апофемы этой пирамиды.

Тогда боковая поверхность вписанной пирамиды равна 1 / 2 (р + р
1) l

При неограниченном возрастании числа боковых граней вписанной пирамиды периметры р
и р
1 стремятся к пределам, принимаемым за длины С и С 1 окружностей оснований, а апофема l
имеет пределом образующую L усечённого конуса. Следовательно, величина боковой поверхности вписанной пирамиды стремится при этом к пределу, равному (С + С 1) L. Этот предел и принимается за величину боковой поверхности усечённого конуса. Обозначив боковую поверхность усечённого конуса буквой S, будем иметь:

S = 1 / 2 (С + С 1) L

Следствия.

1) Если R и R 1 означают радиусы окружностей нижнего и верхнего оснований, то боковая поверхность усечённого конуса будет:

S = 1 / 2 (2π
R + 2π

R 1) L = π
(R + R 1) L.

2) Если в трапеции OO 1 А 1 А (рис.), от вращения которой получается усечённый конус, проведём среднюю линию ВС, то получим:

ВС = 1 / 2 (OA + O 1 A 1) = 1 / 2 (R + R 1),

R + R 1 = 2ВС.

Следовательно,

S = 2π
BC L,

т. е. боковая поверхность усечённого конуса равна произведению длины окружности среднего сечения на образующую.

3) Полная поверхность Т усечённого конуса выразится так:

T = π
(R 2 + R 1 2 + RL + R 1 L)

Мы знаем, что такое конус, попробуем найти площадь его поверхности. Зачем нужно решать такую задачу? Например, нужно понять, сколько теста пойдет на изготовление вафельного рожка? Или сколько кирпичей понадобится, чтобы сложить кирпичную крышу замка?

Измерить площадь боковой поверхности конуса просто так не получится.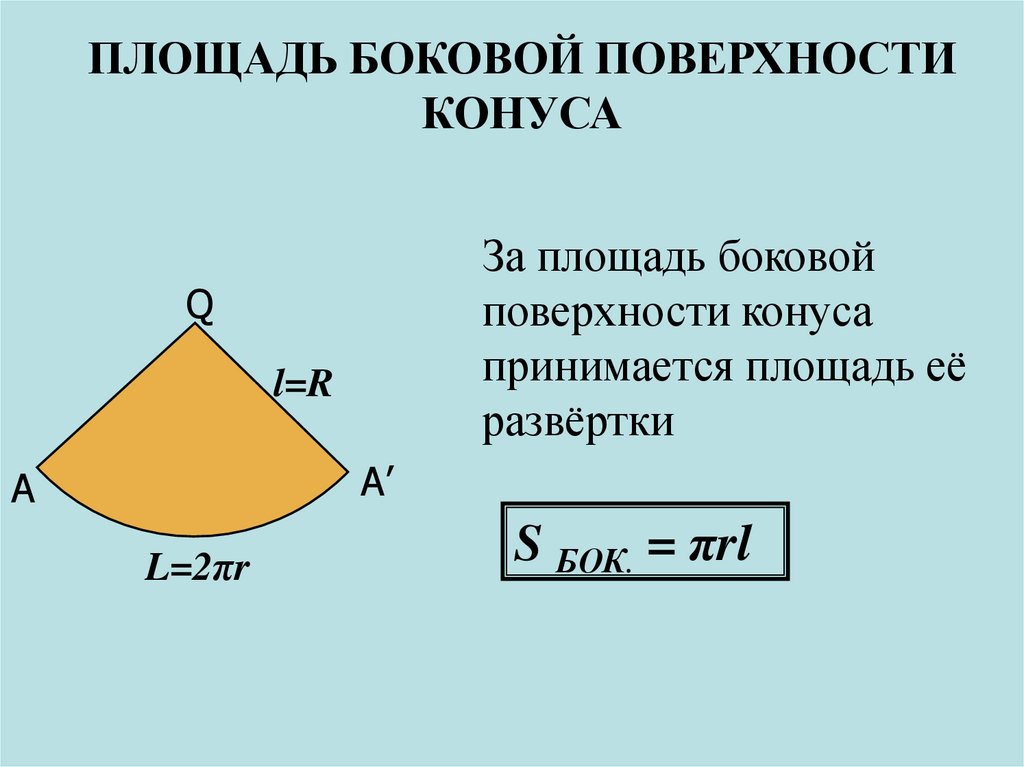 Но представим себе все тот же рожок, обмотанный тканью. Чтобы найти площадь куска ткани, нужно разрезать и разложить ее на столе. Получится плоская фигура, ее площадь мы сможем найти.

Рис. 1. Разрез конуса по образующей

Сделаем так же с конусом. «Разрежем» его боковую поверхность вдоль любой образующей, например, (см. рис. 1).

Теперь «размотаем» боковую поверхность на плоскость. Получаем сектор. Центр этого сектора — вершина конуса, радиус сектора равен образующей конуса, а длина его дуги совпадает с длиной окружности основания конуса. Такой сектор называется разверткой боковой поверхности конуса (см. рис. 2).

Рис. 2. Развертка боковой поверхности

Рис. 3. Измерение угла в радианах

Попробуем найти площадь сектора по имеющимся данным. Сперва введем обозначение: пусть угол при вершине сектора в радианах (см. рис. 3).

С углом при вершине развертки нам придется часто сталкиваться в задачах. Пока же попробуем ответить на вопрос: а не может ли этот угол получиться больше 360 градусов? То есть не получится ли так, что развертка наложится сама на себя? Конечно же, нет.

Докажем это математически. Пусть развертка «наложилась» сама на себя. Это означает, что длина дуги развертки больше длины окружности радиуса . Но, как уже было сказано, длина дуги развертки есть длина окружности радиуса . А радиус основания конуса, разумеется, меньше образующей, например, потому, что катет прямоугольного треугольника меньше гипотенузы

Тогда вспомним две формулы из курса планиметрии: длина дуги . Площадь сектора: .

В нашем случае роль играет образующая ,
а длина дуги равна длине окружности основания конуса, то есть . Имеем:

Окончательно получаем: .

Наряду с площадью боковой поверхности можно найти и площадь полной поверхности. Для этого к площади боковой поверхности надо прибавить площадь основания. Но основание — это круг радиуса , чья площадь по формуле равна .

Окончательно имеем: ,
где — радиус основания цилиндра, — образующая.

Решим пару задач на приведенные формулы.

Рис. 4. Искомый угол

Пример 1
. Разверткой боковой поверхности конуса является сектор с углом при вершине. Найти этот угол, если высота конуса равна 4 см, а радиус основания равен 3 см (см. рис. 4).

Рис. 5. Прямоугольный треугольник, образующий конус

Первым действием, по теореме Пифагора, найдем образующую: 5 см (см. рис. 5). Далее, мы знаем, что .

Пример 2
. Площадь осевого сечения конуса равна , высота равна . Найти площадь полной поверхности (см. рис. 6).

Здесь представлены задачи с конусами, условие связано с его площадью поверхности. В частности в некоторых задачах стоит вопрос об изменении площади при увеличении (уменьшении) высоты конуса или радиуса его основания. Теория для решения задач в . Рассмотрим следующие задачи:

27135. Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.

Площадь боковой поверхности конуса равна:

Подставляем данные:

75697. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 36 раз, а радиус основания останется прежним?

Площадь боковой поверхности конуса:

Образующая увеличивается в 36 раз. Радиус остался прежним, значит длина окружности основания не изменилась.

Значит площадь боковой поверхности изменённого конуса будет иметь вид:

Таким образом, она увеличится в 36 раз.

*Зависимость прямолинейная, поэтому эту задачу без труда можно решить устно.

27137. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 1,5 раза?

Площадь боковой поверхности конуса равна:

Радиус уменьшается в 1,5 раза, то есть:

Получили, что площадь боковой поверхности уменьшилась в 1,5 раза.

27159. Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на Пи.

Полная поверхность конуса:

Необходимо найти радиус:

Известна высота и образующая, по теореме Пифагора вычислим радиус:

Таким образом:

Полученный результат разделим на Пи и запишем ответ.

76299. Площадь полной поверхности конуса равна 108. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

Сечение проходит через середину высоты параллельно основанию. Значит радиус основания и образующая отсеченного конуса будут в 2 раза меньше радиуса и образующей исходного конуса. Запишем чему равна площадь поверхности отсечённого конуса:

Получили, что она будет в 4 раза меньше площади поверхности исходного, то есть 108:4 = 27.

*Так как исходный и отсечённый конус являются подобными телами, то также можно было воспользоваться свойством подобия:

27167. Радиус основания конуса равен 3, высота равна 4. Найдите площадь полной поверхности конуса, деленную на Пи.

Формула полной поверхности конуса:

Радиус известен, необходимо найти образующую.

По теореме Пифагора:

Таким образом:

Результат разделим на Пи и запишем ответ.

Задача. Площадь боковой поверхности конуса в четыре раза больше площади основания. Найдите чему равен косинус угла между образующей конуса и плоскостью основания.

Площадь основания конуса равна:

То есть косинус будет равен:

Ответ: 0,25

Решить самостоятельно:

27136. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?

27160. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах. .

27161. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

На этом всё. Успеха вам!

С уважением, Александр.

*Делитесь с друзьями информацией о сайте через социальные сети.

Назад
Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Тип урока:
урок изучения нового материала с применением элементов проблемно-развивающего метода обучения.

Цели урока:

• познавательные:
  
  • ознакомление с новым математическим понятием;
  • формирование новых ЗУН;
  • формирование практических навыков решения задач.
• развивающие:
  
  • развитие самостоятельного мышления учащихся;
  • развитие навыков правильной речи школьников.
• воспитательные:
  
  • воспитание навыков работы в коллективе.

Оборудование урока:
магнитная доска, компьютер, экран, мультимедийный проектор, модель конуса, презентация к уроку, раздаточный материал.

Задачи урока (для учащихся):

• познакомиться с новым геометрическим понятием — конус;
• вывести формулу для вычисления площади поверхности конуса;
• научиться применять полученные знания при решении практических задач.

Ход урока

I этап. Организационный.

Сдача тетрадей с домашней проверочной работой по пройденной теме.

Учащимся предлагается узнать тему предстоящего урока, разгадав ребус (слайд 1)
:

Рисунок 1.

Объявление учащимся темы и задач урока (слайд 2)
.

II этап. Объяснение нового материала.

1) Лекция учителя.

На доске – таблица с изображением конуса. Новый материал объясняется в сопровождении программного материала «Стереометрия». На экране появляется трёхмерное изображение конуса. Учитель даёт определение конуса, рассказывает о его элементах.(слайд 3)
. Говорится о том, что конус – это тело, образованное при вращении прямоугольного треугольника относительно катета. (слайды 4, 5).
Появляется изображение развёртки боковой поверхности конуса. (слайд 6)

2) Практическая работа.

Актуализация опорных знаний: повторить формулы для вычисления площади круга, площади сектора, длины окружности, длины дуги окружности. (слайды 7–10)

Класс делится на группы. Каждая группа получает вырезанную из бумаги развёртку боковой поверхности конуса (сектор круга с присвоенным номером). Учащиеся выполняют необходимые измерения и вычисляют площадь полученного сектора. Инструкции по выполнению работы, вопросы – постановки проблем – появляются на экране (слайды 11–14)
. Результаты вычислений представитель каждой группы записывает в заготовленную на доске таблицу. Участники каждой группы склеивают модель конуса из имеющейся у них развёртки. (слайд 15)

3) Постановка и решение проблемы.

Как вычислить площадь боковой поверхности конуса, если известны только радиус основания и длина образующей конуса? (слайд 16)

Каждая группа производит необходимые измерения и пытается вывести формулу вычисления искомой площади с помощью имеющихся данных. При выполнении этой работы школьники должны заметить, что длина окружности основания конуса равна длине дуги сектора – развёртки боковой поверхности этого конуса. (слайды 17–21)
Используя необходимые формулы, выводится искомая формула. Рассуждения учащихся должны выглядеть примерно таким образом:

Радиус сектора – развёртки равен l,
градусная мера дуги – φ. Площадь сектора вычисляется по формуле длина дуги, ограничивающей этот сектор, равна Радиус основания конуса R. Длина окружности, лежащей в основании конуса, равна С = 2πR. Заметим, что Так как площадь боковой поверхности конуса равна площади развёртки его боковой поверхности, то

Итак, площадь боковой поверхности конуса вычисляется по формуле S БПК = πRl.

После вычисления площади боковой поверхности модели конуса по выведенной самостоятельно формуле представитель каждой группы записывает результат вычислений в таблицу на доске в соответствии с номерами моделей. Результаты вычислений в каждой строке должны быть равны. По этому признаку учитель определяет правильность выводов каждой группы. Таблица результатов должна выглядеть таким образом:

№ модели	I задание	II задание
	(125/3)π ~ 41,67 π
	(425/9)π ~ 47,22 π
	(539/9)π ~ 59,89 π

Параметры моделей:

1. l=12 см, φ =120
   °
   
2. l=10 см, φ =150
   °
   
3. l=15 см, φ =120
   °
   
4. l=10 см, φ =170
   °
   
5. l=14 см, φ =110
   °
   

Приближённость вычислений связана с погрешностями измерений.

После проверки результатов вывод формул площадей боковой и полной поверхностей конуса появляется на экране (слайды 22–26)
, ученики ведут записи в тетрадях.

III этап. Закрепление изученного материала.

1)
Учащимся предлагаются задачи для устного решения на готовых чертежах.

Найти площади полных поверхностей конусов, изображённых на рисунках (слайды 27–32)
.

2) Вопрос:
равны ли площади поверхностей конусов, образованных вращением одного прямоугольного треугольника относительно разных катетов? Учащиеся выдвигают гипотезу и проверяют её. Проверка гипотезы осуществляется путём решения задач и записывается учеником на доске.

Дано:
Δ АВС, ∠С=90°, АВ=с, АС=b, ВС=а;

ВАА», АВВ» – тела вращения.

Найти:
S ППК 1 , S ППК 2 .

Рисунок 5. (слайд 33)

Решение:

1) R=ВС= а
; S ППК 1 = S БПК 1 + S осн 1 = π а с+π а 2 = π а (а + с).

2) R=АС= b
; S ППК 2 = S БПК 2 + S осн 2 = π b с+π b 2 = π b (b + с).

Если S ППК 1 = S ППК 2 , то а 2 +ас = b 2 + bc, a 2 — b 2 + ac — bc = 0, (a-b)(a+b+c) = 0.
Т.к. a, b, c –
положительные числа (длины сторон треугольника), торавенство верно только в случае, если a =
b.

Вывод:
Площади поверхностей двух конусов равны только в случае равенства катетов треугольника.(слайд 34)

3) Решение задачи из учебника: № 565.

IV этап. Подведение итогов урока.

Домашнее задание:
п.55, 56; № 548, № 561. (слайд 35)

Объявление поставленных оценок.

Выводы по ходу урока, повторение основных сведений, полученных на уроке.

Литература
(слайд 36)

1. Геометрия 10–11 классы – Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др., М., «Просвещение», 2008.
2. «Математические ребусы и шарады» – Н.В. Удальцова, библиотечка «Первого сентября», серия «МАТЕМАТИКА», выпуск 35, М., Чистые пруды, 2010.

Тела вращения, изучаемые в школе, — это цилиндр, конус и шар.

Если в задаче на ЕГЭ по математике вам надо посчитать объем конуса или площадь сферы — считайте, что повезло.

Применяйте формулы объема и площади поверхности цилиндра, конуса и шара. Все они есть в нашей таблице. Учите наизусть. Отсюда начинается знание стереометрии.

Иногда неплохо нарисовать вид сверху. Или, как в этой задаче, — снизу.

Еще один важный момент. Помним, что в задачах части В вариантов ЕГЭ по математике ответ записывается в виде целого числа или конечной десятичной дроби. Поэтому никаких или у вас в ответе в части В быть не должно. Подставлять приближенное значение числа тоже не нужно! Оно обязательно должно сократиться!. Именно для этого в некоторых задачах задание формулируется, например, так: «Найдите площадь боковой поверхности цилиндра, деленную на ».

А где же еще применяются формулы объема и площади поверхности тел вращения? Конечно же, в задаче С2 (16). Мы тоже расскажем о ней.

6.3. Площадь поверхности цилиндра, конуса и сферы

6.3. Площадь поверхности цилиндра, конуса и сферы

Мы знаем, что если боковую поверхность цилиндра разрезать по образующей, то её можно будет развернуть на плоскость. Развёрткой является прямоугольник со сторонами H и L, где H — высота цилиндра, L — длина окружности основания, т. е. L = 2pR, где R — радиус окружности основания. Из этого следует, что площадь боковой поверхности цилиндра выражается формулой

Sбок. ц = 2pRH.(11)

Аналогично получается формула площади боковой поверхности конуса. Развёрткой боковой поверхности конуса, если её разрезать по образующей, является круговой сектор радиусом l, где l — длина образующей конуса. Длина круговой границы этого сектора равна длине окружности основания конуса, т. е. 2pR, где R — радиус основания конуса. Таким образом, из этого следует (вспомните выражение площади кругового сектора через длину дуги и радиус), что площадь боковой поверхности конуса выражается формулой

Sбок. к = pR l.(12)

Исходя из формулы объёма шара, можно получить формулы площади поверхности шара — сферы. Это можно сделать, например, следующим образом. Рассмотрим произвольный многогранник, описанный около сферы, имеющей радиус R. Тогда (см. формулу (5), § 5.6) объём многогранника выражается формулой

Vм = R Sм,

где Sм — площадь поверхности многогранника.

Увеличивая число граней многогранника так, что площадь каждой грани неограниченно уменьшается (стремится к нулю), получим, что формула (5) остаётся верной для шара, и объём шара выражается формулой

Vш = R Sсф, pR 3 = R Sсф.

Таким образом, площадь сферы выражается формулой

Sсф = 4pR 2.(13)

Замечание. В § 6.5 мы выведем формулу площади сферы другим способом.

Задачи, задания, вопросы

1. Сечением цилиндра является квадрат. Основание конуса совпадает с одним из оснований цилиндра, а его вершина — с центром другого. Найдите отношение боковых поверхностей конуса и цилиндра.

2.Из цилиндра с высотой h и радиусом основания R удалили два конуса. Вершина каждого совпадает с центром цилиндра, а основания — с основаниями цилиндра. Найдите площадь полной поверхности получившегося тела.

3.Рассмотрим два тела, получающихся в результате вращения ромба со стороной 1 и острым углом a вокруг меньшей и большей диагоналей. Найдите площадь полной поверхности каждого из них. У какого тела полная поверхность больше?

4(в). Имеются шар и куб равного объёма. У какого тела больше полная поверхность?

5(в). Пусть S — площадь основания конуса, Sбок. к — площадь его боковой поверхности, a — угол между образующей конуса и его основанием. Докажите, что S = Sбок. к  cos a.

6. В прямоугольном треугольнике ABC гипотенуза AB равна 4, ⦞BAC = 30°, K — середина BC. Найдите объём и полную поверхность тела, получающегося при вращении треугольника BAK вокруг AC.

7(т). Через центр правильного треугольника со стороной a проходит прямая, параллельная одной из его сторон. Найдите объём и полную поверхность тела, получающегося при вращении треугольника вокруг этой прямой.

8(п). Центр шара радиуса R лежит на ребре двугранного угла величиной a. Найдите объём части шара и площадь части сферы, находящихся внутри этого угла.

Площадь основания конуса

LearnPracticeDownload

Площадь основания конуса определяется как площадь плоской поверхности (нижней поверхности) конуса. Конус — это трехмерный объект, который плавно сужается от плоского основания (обычно круглого) к точке, называемой вершиной. Другими словами, это фигура, образованная набором отрезков, идущих от основания и соединяющихся в общую точку. Эти линии начинаются от точек в основании и заканчиваются на вершине. В этом уроке мы подробнее обсудим площадь основания конуса.

1.	Что такое площадь основания конуса?
2.	Площадь основания конуса Формула
3.	Как найти площадь основания конуса?
4.	Часто задаваемые вопросы о базовой области конуса

Что такое площадь основания конуса?

Основание конуса представляет собой плоскую грань, представляющую собой круг, поэтому площадь основания конуса представляет собой не что иное, как площадь этого круга. Конус представляет собой трехмерную форму. Площадь поверхности конуса – это пространство, занимаемое криволинейной поверхностью и поверхностью основания конуса.

Площадь основания конуса Формула

Для данного конуса с известным радиусом основания площадь основания (или площадь плоской поверхности) равна π, умноженной на квадрат радиуса, и может быть также представлена ​​как A = πr ² , где r — радиус основания. Площадь основания конуса также может быть выражена через диаметр конуса, что дает формулу A = π(D/2) ² = (πD ² )/4, где D — диаметр конуса. база.

Как найти площадь основания конуса?

Площадь основания конуса можно определить по формуле π r ² . Таким образом, мы следуем шагам, показанным ниже, чтобы найти площадь основания конуса.

• Шаг 1: Определите радиус основания конуса и назовите этот радиус как r.
• Шаг 2: Если радиус задан, найдите площадь основания конуса, используя следующую формулу площади основания конуса A = πr ² . В противном случае, если диаметр задан, найдите площадь основания конуса, используя следующую формулу площади основания конуса = (π/4) D ² . Используйте π = 22/7 или 3,14

.

• Шаг 3: Представьте окончательный ответ в квадратных единицах.

Пример: Чему равна площадь основания конуса, имеющего радиус основания = 4 единицы? (Используйте π = 3,14)

Решение: Учитывая, что r = 4 единицы
Таким образом, площадь основания конуса = π × r ² = 3,14 × 4 ² = 50,24 единицы ²

Ответ: Площадь основания конуса = 50,24 единицы ²

Примеры площади основания конуса

1. Пример 1: Найдите площадь основания конуса с радиусом основания 21 единица. (Используйте π = 22/7)

   Решение: Учитывая, что радиус основания конуса = 21 единица

   Площадь основания данного конуса = π × r ² = (22/7) × 21 ² = 22 × 21 × 3 = 1386 единиц ²

   Ответ: Площадь основания данного конуса 1386 единиц ²

2. Пример 2: Найдите площадь основания конуса, имеющего высоту = 15 единиц и высоту наклона = 17 единиц. (Используйте π = 3.14)

   Решение: При h = 15 единиц и L = 17 единиц

   Радиус конуса (r) = √(L ² — h ² ) = √(17 2 — 15 ² ) = √(289 — 225) = √64 = 8 единиц
   ⇒ Площадь основания данного конуса = π × r ² = 3,14 × 8 ² = 200,96 единиц ²

   Ответ: Площадь основания данного конуса 200,96 единиц ²

перейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по площади основания конуса

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о базовой области конуса

Что такое площадь основания конуса?

Основание конуса — это величина, показывающая площадь, покрытую круглым основанием конуса. Конус — это трехмерный объект, который плавно сужается от плоского основания (обычно круглого) к точке, называемой вершиной. Другими словами, это фигура, образованная набором отрезков, идущих от основания и соединяющихся в общую точку. Эти линии начинаются от точек в основании и заканчиваются на вершине.

Какая формула для площади основания конуса?

Формула площади основания конуса: A = πr ² , где r — радиус основания конуса. Формула площади основания конуса также может быть представлена ​​через диаметр конуса как база.

Как найти площадь основания конуса?

Мы можем найти площадь основания конуса, используя следующие шаги

• Шаг 1: Определите радиус основания конуса.
• Шаг 2: Найдите площадь основания конуса, используя следующую формулу площади основания конуса A = πr ² .
• Шаг 3: Запишите полученный ответ в квадратных единицах.

Как найти площадь основания конуса с диаметром?

Мы можем найти площадь основания конуса с диаметром, используя следующие шаги

• Шаг 1: Определите диаметр основания конуса.
• Шаг 2: Найдите площадь основания конуса, используя следующую формулу площади основания конуса A = (π/4) D ² .
• Шаг 3: Запишите полученный ответ в квадратных единицах.

Как найти площадь основания конуса с наклонной высотой?

Мы можем найти площадь основания конуса с наклонной высотой, используя следующие шаги

• Шаг 1: Определите радиус основания и наклонную высоту конуса.
• Шаг 2: Используйте теорему Пифагора, чтобы получить соотношение L = √(r ² + h ² ), где r — радиус основания, L — наклонная высота, а h — высота конуса.
• Шаг 2: После получения необходимых значений найдите площадь основания конуса по формуле A = πr ² .
• Шаг 3: Запишите ответ в квадратных единицах.

Как найти радиус конуса, если известна площадь основания конуса?

Мы можем найти радиус конуса, если известна площадь основания конуса, используя следующие шаги

• Шаг 1: Определите заданные размеры конуса и примите радиус конуса как «r»
• Шаг 2: Подставьте данные значения в формулу A = πr ² .
• Шаг 3: Найдите «r».
• Шаг 4: Запишите полученный ответ в единицах.

Что произойдет с площадью основания конуса, если радиус основания увеличить вдвое?

Площадь основания конуса увеличивается в четыре раза, если радиус основания удваивается, поскольку «r» в формуле заменяется на «2r» по формуле A = πr ² = π(2r) ² = 4 (πr ² ), что в четыре раза превышает исходное значение площади основания конуса.

Загрузить БЕСПЛАТНЫЕ учебные материалы

Рабочий лист по площади

Рабочие листы по математике и
наглядная программа

Площадь поверхности конуса: значение, уравнение и формула

Допустим, вы хотите решить площадь поверхности рожка мороженого . Есть несколько вещей, которые вы, возможно, захотите узнать, прежде чем начать, например: «Почему вы хотите вычислить площадь поверхности рожка мороженого?» или, после того разговора, «как нам рассчитать площадь поверхности конуса?». Чтобы ответить на этот вопрос, вам понадобится формула для площади поверхности конуса, радиуса и наклонной длины конуса мороженого. Вот что мы собираемся рассказать здесь.

Какова площадь поверхности конуса?

Площадь поверхности конуса — это общая площадь поверхности, покрытая обеими его сторонами, то есть сумма площади его круглого основания и его криволинейной поверхности.

Попробуйте представить, как выглядит конус, подумайте о теле или сторонах конуса. Это даст вам представление о задаче.

Какой из следующих объектов, скорее всего, будет иметь коническую поверхность — шар, воронка, тарелка или кровать?

Решение:

Из списка предметов только воронка имеет коническую поверхность.

Площадь криволинейной поверхности конуса

Площадь криволинейной поверхности конуса — это площадь тела конуса без основания. Здесь очень важна наклонная высота конуса.

Иллюстрация площади криволинейной поверхности конуса, StudySmarter Originals

Вычисление площади криволинейной поверхности конуса

Площадь криволинейной поверхности конуса рассчитывается путем умножения пи на радиус и наклонную высоту конуса.

Следовательно, площадь криволинейной поверхности конуса (A_{cs}) определяется как:

[A_{cs}=pi rl]

где (r) — радиус круглого основания конуса, а (l) — наклонная высота конуса.

Найдите площадь криволинейной поверхности конуса радиусом (7, см) и наклонной высотой (10, см).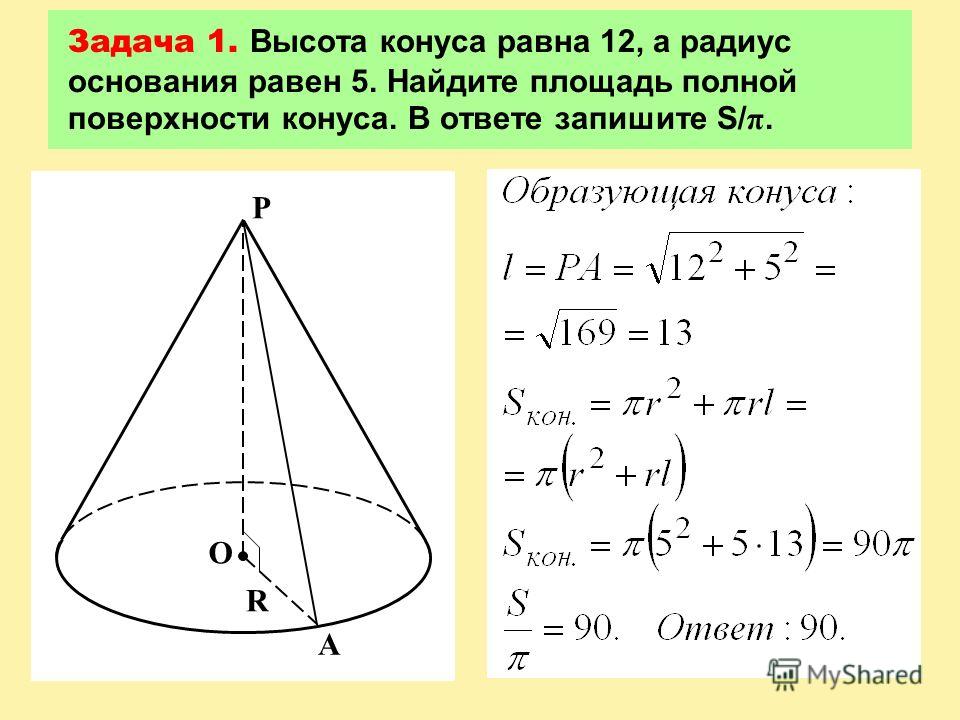 Возьмем (pi=frac{22}{7})

Решение:

Поскольку пи, радиус и наклонная высота заданы, вы должны применить формулу. Отсюда площадь криволинейной поверхности конуса вычисляется как

[A_{cs}=frac{22}{7}times 7, cm times 10, cm] 92]

Площадь поверхности конуса формула

Как указывалось ранее, площадь поверхности конуса равна суммарной общей площади поверхности его криволинейной поверхности и круглого основания , поэтому мы можем сделать некоторые логические предположения относительно какой может быть формула, но мы скоро займемся ее выводом. Однако вот формула, которую вы должны знать:

В этом случае «a» — это общая площадь поверхности, «r» — радиус круглого основания, а «l» — длина криволинейной поверхности ( обычно называется наклонной высотой). л это не внутренняя высота, это два разных измерения. На изображении ниже показано это в случае с конусом, чтобы дать вам лучшее понимание.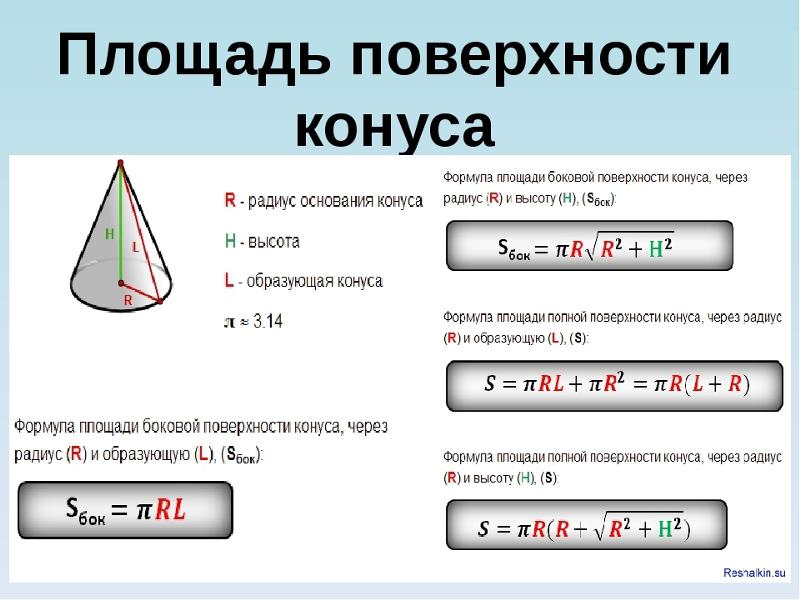

Диаграмма конуса с надписями, StudySmarter Originals

Если вам известна внутренняя высота конуса, вы можете использовать теорему Пифагора для расчета наклонной длины.

Иллюстрация того, как высота наклона получается из радиуса и высоты, StudySmarter Originals

Площадь поверхности конуса

Теперь, когда мы знаем формулу, мы должны поговорить о том, как мы можем вывести ее из некоторых других битов информации. Предполагая, что мы разделили сторону (сторону наклонной высоты) конуса и разложили ее, мы получили то, что показано на диаграмме ниже.

Главное, что нам нужно помнить, это то, что конус можно разбить на две части: круглое основание и коническую часть или изогнутую поверхность.

Иллюстрация расчета общей площади поверхности конуса, StudySmarter Originals

1. Разделите изогнутую поверхность и круглое основание. Вам проще рассчитать площадь поверхности каждой детали отдельно. Забудьте о разделе круга, пока вы к нему вернетесь.
2. Если вы возьмете коническую часть и развернете ее, вы увидите, что на самом деле это сектор большего круга с радиусом l. Следовательно, длина окружности этого большего круга равна площади. Длина дуги сектора у вас такая же, как длина окружности исходного участка круга, т.е.

3. Отношение между площадью всего круга и отношением площади сектора такое же, как отношение между всей окружностью и частью окружности сектора. Если вы возьмете площадь сектора за «а», вы можете выразить это уравнением: [frac{a}{целое, окружность, площадь}=frac{дуга, длина}{целое , окружность, окружность}]

4. Мы подставляем значения из шага 2 в уравнение слова из шага 3:

5. На этом шаге мы просто посмотрим, что нам нужно сделать, чтобы упростить вышеизложенное. уравнение.

   В правой части обе части сокращаются:

   Затем мы умножаем обе части на:

   Это позволяет нам сократить некоторые единицы:

   И у нас остается:

   3

   3

6. Помните наш круг раньше? Ну, площадь круга и площадь нашего конического сечения , поэтому, если мы возьмем обе эти площади и объединим их, мы получим общую площадь поверхности конуса, которая составляет:

Нахождение площади поверхности конуса

Учитывая конус с радиусом основания 7 футов и внутренней высотой 12 футов, рассчитайте площадь поверхности.

Решение:

Поскольку нам известна внутренняя высота, нам нужно использовать теорему Пифагора для вычисления наклонной высоты: Мы можем взять формулу и посмотреть, какие числа мы можем в нее подставить:

7 — наш радиус r и наша наклонная высота l.

Таким образом, наш окончательный ответ в этом случае будет таким, поскольку площадь измеряется в единицах ² .

Учитывая конус с диаметром основания 14 футов и внутренней высотой 18 футов, рассчитайте площадь поверхности.

Решение:

В этом случае нам нужно быть осторожными, так как длина дна указана как диаметр, а не радиус. Радиус — это просто половина диаметра, поэтому радиус в данном случае равен 7 футам. Опять же, нам нужно использовать теорему Пифагора для вычисления наклонной высоты:

Наклонная высота =

Возьмем формулу и заменим r на 7 и l на:

Следовательно, наш окончательный ответ: вашей способности решать вопросы на поверхности конусов, вам рекомендуется практиковать больше задач.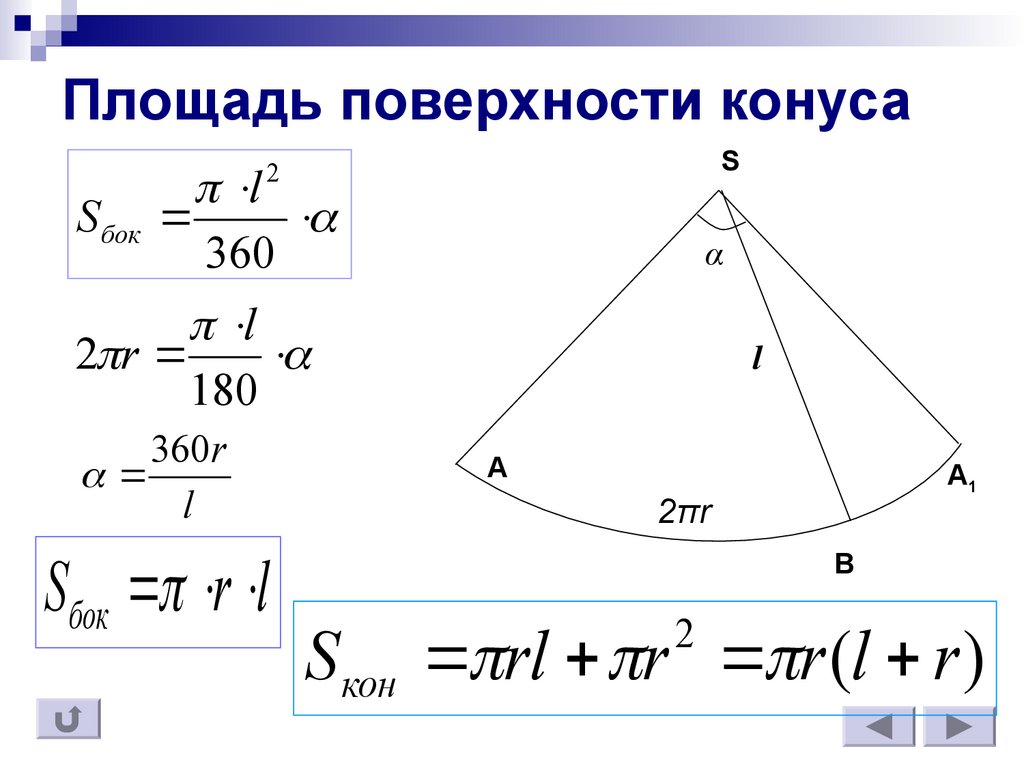

Из приведенного ниже рисунка найдите площадь криволинейной поверхности конуса.

Примеры изогнутых поверхностей без высоты наклона, StudySmarter Originals 92) и массы (10, кг). Если ладонь наклонена под углом (30°) к горизонту, а расстояние до основания конического подвоя плодов пальмы равно (100, м). Найдите массу пальмового листа, необходимого для покрытия запаса пальмовых плодов. Возьмем (pi=3.14).

Решение:

Сделайте набросок рассказа.

Это история или вопрос? Не уверен, просто решите

Нахождение площади конуса с заданным углом, StudySmarter Originals

Таким образом, вы можете использовать SOHCAHTOA, чтобы получить наклонную высоту с

[costheta=frac{adjacent}{гипотенуза}]

(50, м) было получено путем деления базового расстояния на два, так как нам нужен радиус.

[cos(30°)=frac{50, м}{l}]

Перекрестное умножение

Обратите внимание, что [cos(30°)=0,866]

[0,866l =50, м]

Разделите обе стороны на (0,866), чтобы получить наклонную высоту, (l)

[l=57,74, м]

Теперь вы можете найти общую поверхность площадь конического штока, зная, что

[a=pi r^2+pi rl] 92}]

[N_{pf}=2819,2, листьев]

При весе каждой пальмовой ветви (10, кг) общая масса листа, необходимая для покрытия конусообразных плодов пальмы, (M_{pf}) равно:

[M_{pf}=2819,2 times 10, кг]

[M_{pf}=28192, кг]

Следовательно, масса пальмовой ветви для покрытия среднего конического запаса плодов пальмы в Икедуру составляет (28192, кг).