Как найти площадь основания многоугольника формула - Исправление недочетов и поиск решений вместе с Examum.ru

In geometry, the bottom of a three-dimensional object is called a base – if the top of the solid is parallel to the bottom it is also called a base. Since bases occupy a single plane, they have only two dimensions. You can find the area of a base by using the formula for the area of that shape.

Square Bases

Cubes and square pyramids have bases that are square-shaped. The area of a square is equal to the length of one of its sides multiplied by itself, or squared. The formula is A = s². For example, to find the area of a base of a cube with 5-inch sides: A = 5 inches x 5 inches = 25 square inches

Rectangular Bases

Some rectangular solids and pyramids have rectangular bases. The area of a rectangle is equal to its length, l, multiplied by its width, w: A = l x w. Given a pyramid whose base is 10 inches long and 15 inches wide, find area as follows: A = 10 inches x 15 inches = 150 square inches.

Circular Bases

The bases of cylinders and cones are circular. The area of a circle is equal to the circle’s radius, r, squared then multiplied by a constant called pi: A = pi x r². Pi always has the same value, approximately 3.14. While pi technically has an endless number of decimal places, 3.14 is a good enough estimation for simple calculations. For example, given a cylinder with a radius of 2 inches, you can find the base’s area as follows: A = 3.14 x 2 inches x 2 inches = 12.56 square inches.

Triangular Bases

A triangular prism has a triangular base. Finding a triangle’s area requires two known quantities: base, labeled b, and height, labeled h. Base is the length of one of the triangle’s sides, height is the distance from that side to the opposite corner of the triangle. The area of the triangle is equal to half of the base times the height: A = b x h x 1/2 You could find the area of a triangle with base length of 4 inches and height of 3 inches as follows: A = 4 inches x 3 inches x 1/2 = 6 square inches.

Источник

Формулы объёма и площади поверхности. Многогранники.

Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:

Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
Элементарная логика.

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.

Куб		диагональ
Параллелепипед	$V=S_text{OCH}h, h -$ высота
Прямоугольный параллелепипед		$d=sqrt{a^2+b^2+c^2}$
Призма	$V=S_text{OCH}h$	$S = 2S_text{OCH}+$
Пирамида	$V=frac{1}{3}S_text{OCH}h$	$S = S_text{OCH}+$

Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Решение:

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб

Очевидно, их 6, поскольку у куба 6 граней.

Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.

Разберем задачи, где требуется найти площадь поверхности многогранника.

Мы рассмотрим призмы и пирамиды. Начнем с призмы.

Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.

Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.

Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Многогранник на рисунке – это прямая призма с высотой 12.

$P_text{OCH}=8+6+6+2+2+4=28.$

Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:

(больший квадрат), (маленький прямоугольник), $S_text{OCH}=36+8=44$

Подставим все данные в формулу: и найдем площадь поверхности многогранника:

Ответ: 424.

Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

Решение.

Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:

$P_text{OCH}=4+5+2+1+2+4=18.$

Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:

(большой прямоугольник), $S_text{OCH}=16+2=18$ (маленький прямоугольник).

Найдем площадь полной поверхности:

Ответ: 54

Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

Покажем еще один способ решения задачи.

Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.

И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
куба со стороной 1, без удвоенной площади квадрата со стороной 1:

Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело. Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.

Ответ: 42

Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.

Решение.

Пусть АВ = 5 см, ВС = 3 см, тогда $angle{ABC}=120^{circ}$

Из по теореме косинусов найдем ребро АС:

$AC^2=AB^2+BC^2-2cdot ABcdot BC cdot cos120^{circ}$

$AC^2=25+9-2cdot5cdot3cdotleft(-frac{1}{2}right)=47, ~AC = 7$

Отрезок АС – большая сторона , следовательно, большая боковая грань призмы.

Поэтому или откуда h=5.

Ответ: 75

Теперь две задачи на площадь боковой поверхности пирамиды.

Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.

Решение.

Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.

Проведем , тогда (по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.

– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.

Из прямоугольного получим:

$AK=sqrt{AB^2-BK^2}=sqrt{13^2-5^2}=sqrt{169-25}=sqrt{144}=12.$

Из прямоугольного имеем:

$DK=sqrt{DA^2+AK^2}=sqrt{9^2+12^2}=sqrt{81+144}=sqrt{225}=15.$

(по двум катетам), тогда $S_{ADB}=S_{ADC},$ следовательно

$=2S_{ADB}+S_{BDC},$ $=2cdotfrac{1}{2}cdot13cdot9+frac{1}{2}cdot10cdot15=117+75=192.$

Ответ: 192

Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.

Решение:

Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.

Площадь поверхности пирамиды равна

где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.

Значит, полупериметр основания .

Апофему найдем по теореме Пифагора:

$h=sqrt{37^2-12^2}=sqrt{(37-12)(37+12)}=sqrt{25cdot49}=5cdot7=35$

Ответ: 2256

Как решать задачи на нахождение объема многогранника сложной формы?

Покажем два способа.

Первый способ

1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.

Второй способ.

1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.

Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Решение.

1) Достроим составной многогранник до параллелепипеда.

2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:

3) Найдем объем лишней части, то есть маленького параллелепипеда.

Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем

4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:

Ответ: 220.

Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.

Объем призмы равен $V=S_{OCH}cdot h$ , а так как призма прямая, то ее боковое ребро является и высотой, то есть h=6.

Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания

$S_{OCH}=frac{1}{2}cdot ab=frac{1}{2}cdot6cdot7=21.$

Ответ: 126

Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.

Решение.

Объем призмы равен $V = S_{OCH}cdot h$

Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.

Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда. Отношение площадей подобных фигур равно квадрату коэффициента подобия.

Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.

Объем воды не изменился, Так как высота воды h_2 должна быть в 81 раз меньше, чем h_1. Она равна (см).

Ответ: 4

Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды ABDA_1.

Решение.
Опустим из вершины A_1 высоту A_1H Н на основание ABCD.

$=S_{ABCD}cdot A_1H$

$=frac{1}{3}S_{ABD}cdot A_1H$

Диагональ основания делит его на два равных треугольника, следовательно, $S_{ABD}=frac{1}{2}S_{ABCD}.$

Имеем:

$ABDA_1=frac{1}{3}S_{ABD}cdot A_1H=frac{1}{3}cdotfrac{1}{2}S_{ABCD}cdot A_1H=frac{1}{6}V_{ABCDA_1B_1C_1D_1}=frac{1}{6}cdot21=3,5.$

Ответ: 3,5

Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна

Решение.
По формуле объема пирамиды, .

В основании пирамиды лежит правильный треугольник. Его площадь равна $S_{OCH}=frac{a^2sqrt{3}}{4}.$

$S_{OCH}=frac{8^2sqrt{3}}{4}=frac{64sqrt{3}}{4}=16sqrt{3}.$

Объем пирамиды $V=frac{1}{3}cdot16sqrt{3}cdot6sqrt{3}=16cdot6=96.$

Ответ: 96

Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру. Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.

Решение.

По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.

Пусть AD=x, тогда $S_{OCH}=x^2.$

Так как точки М и К – середины АD и DС соответственно, то $DM=DK=frac{x}{2}.$

$S_{MDK}=frac{1}{2}MDcdot DK=frac{1}{2}cdotfrac{x}{2}cdotfrac{x}{2}=frac{1}{8}x^2.$

Площадь треугольника MDK, лежащего в основании новой призмы, составляет $frac{1}{8}$ часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: $V=S_{OCH}cdot h$ , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен 32:8=4.

Ответ: 4

Докажем полезную теорему.

Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.

Доказательство:

Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.

$S=P_{perp}cdot l.$

Больше задач на формулы объема и площади поверхности здесь.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Загрузить PDF

Очень легко вычислить площадь правильного треугольника (это многоугольник!) и очень непросто сделать это в случае неправильного одиннадцатиугольника (это тоже многоугольник!). Данная статья расскажет вам, как вычислять площадь различных многоугольников.

1
Формула для нахождения площади правильного многоугольника: Площадь = 1/2 х периметр х апофема.
- Периметр – сумма сторон многоугольника.
- Апофема – отрезок, соединяющий центр многоугольника и середину любой из его сторон (апофема перпендикулярна стороне).
2

Найдите апофему. Она, как правило, дана в условии задачи. Например, дан шестиугольник, апофема которого равна 10√3.
3
Найдите периметр. Если периметр не дан в условии задачи, то его можно найти по известной апофеме.
- Шестиугольник можно разбить на 6 равносторонних треугольников. Апофема делит одну сторону пополам, создавая прямоугольный треугольник с углами 30-60-90 градусов.
- В прямоугольном треугольнике сторона, противолежащая углу в 60 градусов, равна x√3; углу в 30 градусов равна «х»; углу 90 градусов равна 2x. Если значение стороны x√3 равно 10√3, то х = 10.
- «х» – это половина длины основания треугольника. Удвойте ее и найдете полную длину основания. В нашем примере основание треугольника равно 20 единицам. В свою очередь основание треугольника есть сторона шестиугольника. Таким образом, периметр шестиугольника равен 20 х 6 = 120.
4
Подставьте значения апофемы и периметра в формулу. В нашем примере:
- площадь = 1/2 х 120 х 10√3
- площадь = 60 х 10√3
- площадь = 600√3
5

Упростите ответ. Возможно, вам придется записать ответ в виде десятичной дроби (то есть избавиться от корня). С помощью калькулятора найдите √3 и полученное число умножьте на 600: √3 х 600 = 1039,2. Это ваш окончательный ответ.

Реклама

1
Найдите площадь треугольника. Формула: Площадь = 1/2 х основание х высота.
- Если вам дан треугольник с основанием 10 и высотой 8, то его площадь = 1/2 х 8 х 10 = 40.
2
Найдите площадь квадрата. Чтобы найти площадь квадрата, просто возведите в квадрат длину одной его стороны. Если умножить основание квадрата на его высоту, мы получим тот же ответ, так как основание и высота равны.
- Если сторона квадрата равна 6, то его площадь = 6 х 6 = 36.
3
4
Найдите площадь трапеции. Формула: Площадь = [(основание1 + основание2) х высота] / 2.
- Например, дана трапеция с основаниями 6 и 8 и высотой 10. Ее площадь = [(6 + 8)•10]/2 = (14 х 10)/2 = 140/2 = 70.
Реклама

1

Используйте координаты вершин неправильного многоугольника. Зная координаты вершин, можно определить площадь неправильного многоугольника.
2

Сделайте таблицу. Запишите координаты вершин (х,у) (вершины выбирать последовательно в направлении против часовой стрелки). В конце списка еще раз напишите координату первой вершины.
3

Умножьте значение координаты «х» первой вершины на значение координаты «у» второй вершины (и так далее). Сложите результаты (в нашем примере сумма равна 82).
4

Умножьте значение координаты «у» первый вершины на значение координаты «х» второй вершины (и так далее). Сложите результаты (в нашем примере сумма равна -38).
5

Вычтите сумму, полученную в шаге 4, из суммы, полученной в шаге 3. В нашем примере: (82) — (-38) = 120.
6

Разделите полученный результат на 2, чтобы найти площадь многоугольника: S=120/2 = 60 (квадратных единиц).

Реклама

Советы

Если вы записываете координаты вершин в направлении по часовой стрелке, вы получите отрицательную площадь. Таким образом, это можно использовать для описания цикла или последовательности данного набора вершин, формирующих многоугольник.
Данная формула находит площадь с учетом формы многоугольника. Если многоугольник имеет форму цифры 8, то необходимо из площади с вершинами против часовой стрелки вычесть площадь с вершинами по часовой стрелке.

Об этой статье

Эту страницу просматривали 440 164 раза.

Была ли эта статья полезной?

Источник

Площади фигур. Основные формулы.

Площадь треугольника.

Формула	Рисунок	Расшифровка формулы
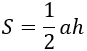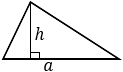		а — основание, h — высота, проведенная к этому основанию. Формула применима для любого треугольника.
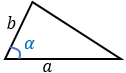		a, b — стороны, α — угол между этими сторонами. Формула применима для любого треугольника.
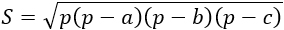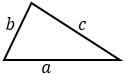		a, b, с — стороны, р — полупериметр (сумма трех сторон, деленная пополам). Формула применима для любого треугольника.
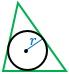		r — радиус вписанной в треугольник окружности, р — полупериметр (сумма трех сторон, деленная пополам). Формула применима для любого треугольника.
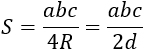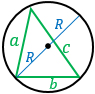		a, b, с — стороны, R — радиус описанной около треугольника окружности, d — диаметр описанной окружности. Формула применима для любого треугольника.
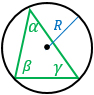		R — радиус описанной около треугольника окружности, α, β, γ — углы треугольника. Формула применима для любого треугольника.
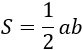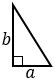		a, b — катеты. Формула применима для прямоугольного треугольника.
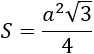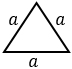		a — сторона. Формула применима для равностороннего (правильного) треугольника.

Площадь квадрата и прямоугольника.

Площадь параллелограмма и ромба.

Формула	Рисунок	Расшифровка формулы
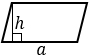		а — одна из сторон параллелограмма, h — высота, проведенная к этой стороне
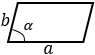		а, b — стороны параллелограмма, α — угол между этими сторонами
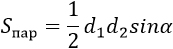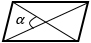		d₁, d₂ — диагонали, α — угол между диагоналями (можно брать любой угол, т.к. синусы смежных углов равны)
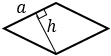		а — сторона ромба, h — высота, проведенная к этой стороне
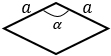		а — сторона ромба, α — угол между этими сторонами
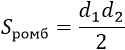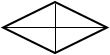		d₁, d₂ — диагонали ромба

Площадь трапеции.

Формула	Рисунок	Расшифровка формулы
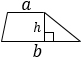		а, b — основания трапеции, h — высота. Формула применима для любой* трапеции.
		m — средняя линия трапеции, h — высота. Формула применима для любой трапеции.
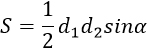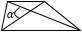		d₁, d₂ — диагонали трапеции, α — угол между диагоналями (можно брать любой угол, т.к. синусы смежных углов равны). Формула применима для любой трапеции.

*Любая трапеция — это и равнобедренная, и прямоугольная, и тупоугольная, и произвольная

Площадь круга и кругового сектора.

Площадь многоугольника.

Формула

Рисунок

Расшифровка формулы

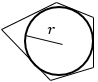р — полупериметр (сумма всех сторон многоугольника, деланная на 2), r — радиус вписанной в этот многоугольник окружности.

*Пятиугольник нарисован для примера.

Формула работает как для правильного, так и для произвольного многоугольника, главное, чтобы в него можно было вписать окружность.

Источник

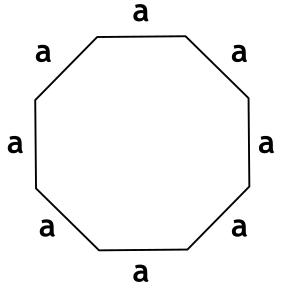
На странице собраны калькуляторы и формулы, которые помогут найти и рассчитать площадь правильного многоугольника по стороне и количеству сторон, а также зная радиус вписанной и описанной окружностей.

Правильный многоугольник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.

Содержание:

калькулятор площади правильного многоугольника
формула площади правильного многоугольника через длину стороны
формула площади правильного многоугольника радиус вписанной окружности
формула площади правильного многоугольника радиус описанной окружности
пример задачи

Формула площади правильного многоугольника через длину стороны и число сторон

S = dfrac{na^2}{4} cdot ctg dfrac{180°}{n}

a — длина стороны многоугольника

n — число сторон многоугольника

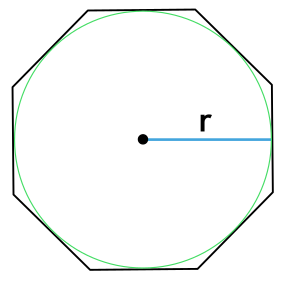
Формула площади правильного многоугольника через радиус вписанной окружности

S = nr^2 tg dfrac{180°}{n}

r — радиус вписанной в многоугольник окружности

n — число сторон многоугольника

Формула площади правильного многоугольника через радиус описанной окружности

S = dfrac{nR^2}{2} cdot sin dfrac{360°}{n}

R — радиус описанной в многоугольник окружности

n — число сторон многоугольника

Пример задачи на нахождение площади правильного многоугольника

Задача 1

Найдите площадь правильного n-угольника, если n = 6, r = 9 см, где r — радиус вписанной окружности.

Решение

Чтобы решить эту задачу мы используем вторую формулу.

S = nr^2 tg dfrac{180°}{n} = 6 cdot 9^2 cdot tg dfrac{180°}{6} = 6 cdot 81 cdot tg 30° = 486 cdot tg 30° = 486 cdot 0.57735027 approx 280.59223 : см^2

Ответ: 486 cdot tg 30° approx 280.59223 : см^2

Чтобы проверить ответ воспользуемся калькулятором .

Источник

Square Bases

Rectangular Bases

Circular Bases

Triangular Bases

Формулы объёма и площади поверхности. Многогранники.

Советы

Похожие статьи

Об этой статье

Была ли эта статья полезной?

Площади фигур. Основные формулы.

Содержание:

Формула площади правильного многоугольника через длину стороны и число сторон

Формула площади правильного многоугольника через радиус вписанной окружности

Формула площади правильного многоугольника через радиус описанной окружности

Пример задачи на нахождение площади правильного многоугольника