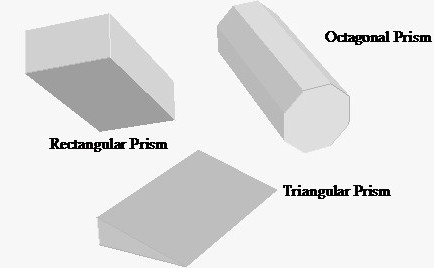
Разные призмы непохожи друг на друга. В то же время у них много общего. Чтобы найти площадь основания призмы, потребуется разобраться в том, какой вид оно имеет.
Общая теория
Призмой является любой многогранник, боковые стороны которого имеют вид параллелограмма. При этом в ее основании может оказаться любой многогранник — от треугольника до n-угольника. Причем основания призмы всегда равны друг другу. Что не относится к боковым граням — они могут существенно различаться по размерам.
При решении задач встречается не только площадь основания призмы. Может потребоваться знание боковой поверхности, то есть всех граней, которые не являются основаниями. Полной поверхностью уже будет объединение всех граней, которые составляют призму.
Иногда в задачах фигурирует высота. Она является перпендикуляром к основаниям. Диагональю многогранника является отрезок, который соединяет попарно две любые вершины, не принадлежащие одной грани.
Следует отметить, что площадь основания прямой призмы или наклонной не зависит от угла между ними и боковыми гранями. Если у них одинаковые фигуры в верхней и нижней гранях, то их площади будут равными.
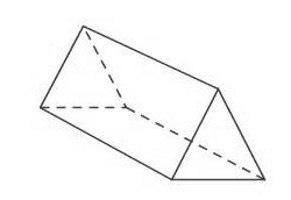
Треугольная призма
Она имеет в основании фигуру, имеющую три вершины, то есть треугольник. Он, как известно, бывает разным. Если треугольник прямоугольный, то достаточно вспомнить, что его площадь определяется половиной произведения катетов.
Математическая запись выглядит так: S = ½ ав.
Чтобы узнать площадь основания треугольной призмы в общем виде, пригодятся формулы: Герона и та, в которой берется половина стороны на высоту, проведенную к ней.
Первая формула должна быть записана так: S = √(р (р-а) (р-в) (р-с)). В этой записи присутствует полупериметр (р), то есть сумма трех сторон, разделенная на два.
Вторая: S = ½ на * а.
Если требуется узнать площадь основания треугольной призмы, которая является правильной, то треугольник оказывается равносторонним. Для него существует своя формула: S = ¼ а2 * √3.
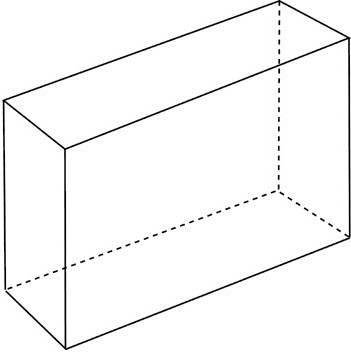
Четырехугольная призма
Ее основанием является любой из известных четырехугольников. Это может быть прямоугольник или квадрат, параллелепипед или ромб. В каждом случае для того, чтобы вычислить площадь основания призмы, будет нужна своя формула.
Если основание — прямоугольник, то его площадь определяется так: S = ав, где а, в — стороны прямоугольника.
Когда речь идет о четырехугольной призме, то площадь основания правильной призмы вычисляется по формуле для квадрата. Потому что именно он оказывается лежащим в основании. S = а2.
В случае когда основание — это параллелепипед, будет нужно такое равенство: S = а * на. Бывает такое, что даны сторона параллелепипеда и один из углов. Тогда для вычисления высоты потребуется воспользоваться дополнительной формулой: на = в * sin А. Причем угол А прилегает к стороне «в», а высота на противолежащая к этому углу.
Если в основании призмы лежит ромб, то для определения его площади будет нужна та же формула, что для параллелограмма (так как он является его частным случаем). Но можно воспользоваться и такой: S = ½ d1 d2. Здесь d1 и d2 — две диагонали ромба.
Правильная пятиугольная призма
Этот случай предполагает разбиение многоугольника на треугольники, площади которых узнать проще. Хотя бывает, что фигуры могут быть с другим количеством вершин.
Поскольку основание призмы — правильный пятиугольник, то он может быть разделен на пять равносторонних треугольников. Тогда площадь основания призмы равна площади одного такого треугольника (формулу можно посмотреть выше), умноженной на пять.
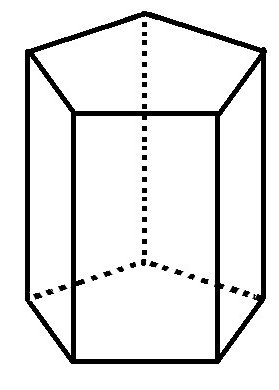
Правильная шестиугольная призма
По принципу, описанному для пятиугольной призмы, удается разбить шестиугольник основания на 6 равносторонних треугольников. Формула площади основания такой призмы подобна предыдущей. Только в ней площадь равностороннего треугольника следует умножать на шесть.
Выглядеть формула будет таким образом: S = 3/2 а2 * √3.
Задачи
№ 1. Дана правильная прямая четырехугольная призма. Ее диагональ равна 22 см, высота многогранника — 14 см. Вычислить площадь основания призмы и всей поверхности.
Решение. Основанием призмы является квадрат, но его сторона не известна. Найти ее значение можно из диагонали квадрата (х), которая связана с диагональю призмы (d) и ее высотой (н). х2 = d2 — н2. С другой стороны, этот отрезок «х» является гипотенузой в треугольнике, катеты которого равны стороне квадрата. То есть х2 = а2 + а2. Таким образом получается, что а2 = (d2 — н2)/2.
Подставить вместо d число 22, а «н» заменить его значением — 14, то получается, что сторона квадрата равна 12 см. Теперь просто узнать площадь основания: 12 * 12 = 144 см2.
Чтобы узнать площадь всей поверхности, нужно сложить удвоенное значение площади основания и учетверенную боковую. Последнюю легко найти по формуле для прямоугольника: перемножить высоту многогранника и сторону основания. То есть 14 и 12, это число будет равно 168 см2. Общая площадь поверхности призмы оказывается 960 см2.
Ответ. Площадь основания призмы равна 144 см2. Всей поверхности — 960 см2.
№ 2. Дана правильная треугольная призма. В основании лежит треугольник со стороной 6 см. При этом диагональ боковой грани составляет 10 см. Вычислить площади: основания и боковой поверхности.
Решение. Так как призма правильная, то ее основанием является равносторонний треугольник. Поэтому его площадь оказывается равна 6 в квадрате, умноженному на ¼ и на корень квадратный из 3. Простое вычисление приводит к результату: 9√3 см2. Это площадь одного основания призмы.
Все боковые грани одинаковые и представляют собой прямоугольники со сторонами 6 и 10 см. Чтобы вычислить их площади, достаточно перемножить эти числа. Потом умножить их на три, потому что боковых граней у призмы именно столько. Тогда площадь боковой поверхности оказывается раной 180 см2.
Ответ. Площади: основания — 9√3 см2, боковой поверхности призмы — 180 см2.
Разные призмы — это не одно и то же. В то же время у них много общего. Чтобы найти площадь основания призмы, нужно выяснить, какой у нее тип.
Содержание
- 1 Общая теория
- 2 Треугольная призма
- 3 Четырехугольная призма
- 4 Правильная пятиугольная призма
- 5 Правильная шестиугольная призма
- 6 Задачи
Общая теория
Призма — это любой многогранник, стороны которого имеют форму параллелограмма. Также у его основания может появиться любой многогранник — от треугольника до n-угольника. Кроме того, основания призм всегда совпадают. Это не касается боковых граней — они могут существенно различаться по размеру.
При устранении неисправностей встречается не только область основания призмы. Может потребоваться знание боковой поверхности, т.е всех граней, не являющихся основанием. Вся поверхность уже будет объединением всех граней, составляющих призму.
Иногда в задачи входит высота. Он перпендикулярен основаниям. Диагональ многогранника — это отрезок, который попарно соединяет две вершины, не принадлежащие одной грани.
Следует отметить, что площадь основания прямой или наклонной призмы не зависит от угла между ними и боковыми гранями. Если у них одинаковые формы на верхнем и нижнем краях, их области будут одинаковыми.
Треугольная призма
В его основании фигура с тремя вершинами, то есть треугольник. Он известен тем, что отличается. Если треугольник прямоугольный, то достаточно помнить, что его площадь определяется половиной произведения ножек.
Математическая запись выглядит так: S = ½ ср.
Для определения площади основания треугольной призмы в общем виде пригодятся формулы: Цапля и та, у которой половина стороны поднята на начерченную на ней высоту.
Первую формулу нужно записать так: S = √ (p (pa) (pc) (pc)). В этой записи есть полупериметр (p), то есть сумма трех сторон, разделенная на два.
Во-вторых: S = ½ на * a.
Если вы хотите узнать площадь основания треугольной призмы, которая является правильной, треугольник получается равносторонним. Для этого есть формула: S = ¼ a2 * √3.
Четырехугольная призма
Его основание — один из известных четырехугольников. Это может быть прямоугольник или квадрат, параллелепипед или ромб. В любом случае для расчета площади основания призмы вам понадобится другая формула.
Если основание — прямоугольник, его площадь определяется следующим образом: S = ab, где a, b — стороны прямоугольника.
При работе с четырехугольной призмой площадь основания обычной призмы рассчитывается по формуле для квадрата. Потому что именно он оказывается внизу. S = a2.
Если основание — параллелепипед, потребуется следующее равенство: S = a * on. Бывает, что задаются сторона параллелепипеда и один из углов. Таким образом, для вычисления высоты потребуется дополнительная формула: at = в * sin A. Кроме того, угол A примыкает к стороне «в», а высота противоположна этому углу.
Если в основании призмы находится ромб, для определения его площади потребуется та же формула, что и для параллелограмма (поскольку это его частный случай). Но вы также можете использовать это: S = ½ d1 d2. Здесь d1 и d2 — две диагонали ромба.
Правильная пятиугольная призма
В этом случае многоугольник разбивается на треугольники, области которых легче обнаружить. Хотя бывает, что фигурки могут быть с разным количеством вершин.
Поскольку основание призмы представляет собой правильный пятиугольник, его можно разделить на пять равносторонних треугольников. Тогда площадь основания призмы равна площади одного из этих треугольников (формулу можно увидеть выше), умноженной на пять.
Правильная шестиугольная призма
Согласно принципу, описанному для пятиугольной призмы, можно разделить основной шестиугольник на 6 равносторонних треугольников. Формула площади основания такой призмы аналогична предыдущей. Только в нем площадь равностороннего треугольника надо умножить на шесть.
Формула будет выглядеть так: S = 3/2 a2 * √3.
Задачи
1. Дана правильная прямоугольная призма. Его диагональ 22 см, высота многогранника 14 см. Вычислите площадь основания призмы и всей поверхности.
Решение. Основание призмы — квадрат, но его сторона неизвестна. Вы можете найти его значение по диагонали квадрата (x), которая связана с диагональю призмы (d) и ее высотой (h) x2 = d2 — n2. С другой стороны, этот отрезок «x» — гипотенуза в треугольнике, катеты которого равны стороне квадрата. То есть x2 = a2 + a2. Отсюда получается, что a2 = (d2 — H2) / 2.
Замените 22 вместо d и замените n на его значение — 14, так получится, что сторона квадрата равна 12 см. Теперь узнайте площадь основания: 12 * 12 = 144 см2.
Чтобы узнать площадь всей поверхности, необходимо прибавить удвоенную площадь основания и учетверить сторону. Последнюю легко найти по формуле прямоугольника: умножьте высоту многогранника на сторону основания. То есть 14 и 12 это число будет равно 168 см2. Общая поверхность призмы 960 см2.
Отвечать. Базовая площадь призмы 144 см2. Вся поверхность 960 см2.
№2. Дана правильная треугольная призма. В основании треугольник со стороной 6 см, в данном случае диагональ боковой грани 10 см. Вычислите площади: основание и боковая поверхность.
Решение. Поскольку призма правильная, ее основание — равносторонний треугольник. Следовательно, его площадь равна 6 в квадрате, умноженному на квадратный корень из 3. Простой расчет приводит к результату: 9√3 см2. Это площадь основания призмы.
Все боковые грани равны и представляют собой прямоугольники со сторонами 6 и 10 см, для расчета их площадей достаточно эти числа умножить. Затем умножьте их на три, потому что у призмы ровно столько боковых граней. Таким образом, боковая поверхность получается 180 см2.
Отвечать. Площади: основание — 9√3 см2, боковая поверхность призмы — 180 см2.
Это трехмерная геометрическая фигура, состоящая из двух равных параллельных многоугольников в качестве основания и боковых граней, которые являются параллелограммами. Они получают конкретное название в зависимости от количества сторон, образующих их основу. Таким образом, мы имеем, например, что если его основания имеют три стороны, это будет треугольная призма, четыре прямоугольные стороны, пять пятиугольных сторон и т. Д.
В данной теме конкретно все, что связано с пятиугольная призма, но необходимо знать общие аспекты призм в целом.
Индекс
- 0.1 Общие характеристики призмы
- 1 Классификация призм
-
- 1.0.1 По количеству сторон их баз классифицируются на:
- 1.0.2 По боковым граням они делятся на:
- 1.0.3 По внутренним углам они подразделяются на
-
- 2 Пятиугольная призма
- 2.1 Характеристики
- 2.2 Как рассчитать площадь правильной пятиугольной призмы
- 2.3 Как найти значение ап (апофемы) пятиугольной призмы?
- 2.4 Площадь неправильной пятиугольной призмы
- 2.4.1 Формула площади неправильной пятиугольной правой призмы:
- 2.4.2 Площадь наклонной пятиугольной призмы
- 2.5 Объем пятиугольной призмы
- 2.6 Как сделать прямую правильную пятиугольную призму
- 2.6.1 Пятиугольный базовый ход
- 2.6.2 След призмы
Общие характеристики призмы
Элементы, составляющие призму:
- Основы Это два параллельных и равных многоугольника, образующих пол и верх призмы. Число его сторон может быть различным, и именно они дают призме имя и фамилию.
- Боковые грани: — параллелограммы, отделяющие нижнее основание от верхнего.
- Рост Это расстояние, разделяющее две базы.
- Края: Каждая из сторон многоугольников, образующих основания, называется ребрами основания. И каждая из сторон боковых граней называется индивидуально боковой кромкой.
- Вершина: Каждая из точек пересечения ребер называется вершиной.
Классификация призм
Призма классифицируется по свойствам основания:
- Regular:Это тот, чья основа представляет собой многоугольник, у которого все стороны равны, а его внутренние углы равны.
- Нерегулярный: Это тот, основания которого представлены многоугольниками с разными сторонами и внутренними углами.
По количеству сторон их баз классифицируются на:
- Треугольник с 3-х сторон
- Четырехугольник 4-х сторонний
- Пятиугольная 5 сторон
- Шестигранник с 6 сторон
- Семиугольная 7 сторон
- Восьмиугольная 8 сторон
- 9-сторонний eneagon или nonagon
- Десятиугольник 10 сторон … и так далее.
По боковым граням они делятся на:
- Правая призма: Это тот, у которого столько же боковых граней, сколько и у его основания, они прямоугольные и параллельны ему.
- Наклонный: Наклонная призма не имеет перпендикулярности на боковых сторонах по отношению к основанию. Его боковые грани ромбовидные. Их особенность в том, что их высота не совпадает со значением их боковых краев.
По внутренним углам они подразделяются на
Выемки: Призма может быть классифицирована как вогнутая, если ее внутренние углы превышают 180 °. Из-за его неправильной формы, которая дает вид щели внутрь призмы, если мы пересечем ее прямой линией, она может быть прорезана более чем в одной точке.
Выпуклый: Призма является выпуклой, когда ее внутренние углы составляют менее 180 °, и, с другой стороны, мы имеем, что при пересечении ее линией она разрезает только в двух уникальных точках.
Пятиугольная призма
Теперь мы готовы узнать больше о пятиугольной призме. После определения характеристик, общих для каждой призмы, мы подробно рассмотрим пятиугольную призму. Пятиугольная призма — это призма, основания которой равны и параллельны пятиугольникам и пяти параллелограммам, образующим ее боковые грани.
Характеристики
Пятиугольная призма имеет следующие характеристики:
- Основы. Он состоит из двух параллельных и равных пятиугольников.
- Карас. У него пять боковых граней плюс два основания, всего семь граней,
- Высота. Это расстояние между двумя базами.
- Вершина. Это точки призмы, где три грани совпадают, всего 10 вершин.
- Края. Они являются точками встречи двух граней призмы, всего у нее 15 граней.
Согласно теореме Эйлера существует взаимосвязь между количеством граней (C), ребер (A) и вершинами каждой призмы, внутренние углы которой меньше 180 ° (выпуклые).
Применяя формулу A = C + V-2, можно найти количество граней пятиугольной призмы: А = 7 + 10-2 = 15
Как Рассчитайте площадь правильной пятиугольной призмы
Его основания равны правильным пятиугольникам и равны прямоугольным сторонам, поэтому расчет его площади определяется по формуле:
Площадь = 5. L. (ap. + H), где L — размер одной из сторон пятиугольника, ap. (апофема) — это кратчайшее расстояние от центра до любой стороны, а h — высота призмы.
Как найти значение ап (апофемы) пятиугольной призмы?
Это переменная, которую мы не знаем так очевидно, как другие. Вот математическая формула, чтобы найти это.
Зная количество сторон (N) и их размер (L), сначала вычислите центральный угол, который образуется между центром многоугольника и двумя последовательными вершинами, например:
? = 360 ° / с.
пример: центральный угол пятиугольника? = 360 ° / 5 равно 72 °.
Далее идет апофема
Разделив размер одной из сторон (L) на двойную тангенс половины центрального угла (?)
ap = L / 2 x тангаж (? / 2)
Пример: имея пятиугольную призму, стороны которой имеют размер 20 см и 30 сантиметров в высоту, давайте найдем ее площадь. Мы уже знаем, что значение центрального угла правильного пятиугольника составляет 72 °. Найдем его апофему:
Ар = 20/2 х Тан (72/2)
Ар = 20/2 х Тан (36)
Ар = 20/2 х (0.73)
Ap = 20 / 1.46
Ap = 13,69 см.
Теперь да, у нас есть все данные для определения вашего района:
Площадь = 5 x L x (ap + h)
5 х 20 (13,69 + 30)
100 (43,69)
Площадь = 4369 см.
Площадь неправильной пятиугольной призмы
Принимая во внимание, что неправильная пятиугольная призма имеет в основе два неправильных пятиугольника, необходимо найти площадь неправильного пятиугольника (Ab), его периметр (Pb) и высоту призмы, чтобы впоследствии рассчитать площадь неправильного пятиугольника. Призма.
Формула площади неправильной пятиугольной правой призмы:
Площадь призмы = 2. Ab + Pb. час
Площадь основания неправильного пятиугольника (Ab) находится через метод триангуляция, что означает деление его на более мелкие треугольные фигуры для вычисления их площадей, и, таким образом, более легко получить общую площадь пятиугольника, сложив их все.
Периметр неправильного основания пятиугольника (Pb) Его можно найти, сложив размеры его пяти сторон.
Площадь наклонной пятиугольной призмы
Формула расчета площади для этого типа призмы отличается от формулы для правой пятиугольной призмы.
Площадь оснований рассчитывается так же, как и в прямой кишке, разница заключается в сторонах из-за того, что они наклонены.
Площадь одной из сторон наклонной пятиугольной призмы рассчитывается на основе измерения бокового края и периметра призмы. прямое сечение призмы.
Пересечение плоскости с призмой под углом 90 ° с каждой из боковых граней является прямым участком призмы. То есть при поперечном делении призмы наблюдается именно плоское основание.
Чтобы найти графическое представление прямой участок наклонной призмы Кто угодно, поместите квадрат, опираясь на один из его краев, и, образуя угол 90 °, проведите линию, доходящую до соседнего края, и так далее с другими краями. Как только эта процедура будет выполнена, эту поверхность можно будет визуализировать на плоскости.
Площадь = 2. Ab + Psr. к
где Ab площадь основания, Пср — периметр прямого участка призмы и a боковой край.
Чтобы определить значение периметра прямого участка, достаточно выровнять одну из его кромок под углом 90 °, измерить расстояние от этой кромки до того места, где она пересекает параллельную кромку, и сложить его пять раз.
Объем пятиугольной призмы
Для расчета объема пятиугольной призмы, как прямой, так и наклонной, применяется общая формула для всех типов призм: умножьте площадь основания (Ab) на высоту (h).
Объем = Ab. час
Подставив Ab его собственной формулой, получим Volume = 5. L. ap / 2. час
Помните, что в правой призме измерение высоты равно измерению бокового края. в то время как в наклонной призме высота призмы не совпадает с размером боковой кромки, независимо от типа призмы, будьте осторожны, чтобы не перепутать.
Как сделать прямую правильную пятиугольную призму
? = Внутренний угол 108 °, образованный между двумя сторонами пятиугольника основания (фиксированное измерение для пятиугольной фигуры)
L = сторона
H = высота
Пятиугольный базовый ход
Прежде чем приступить к рисованию призмы, необходимо определить ее основания. Легко и не очень технично я объясню, как сделать правильную пятиугольную фигуру.
- проведите прямую линию, которая будет служить отправной точкой (рис. 1)
- отметьте размер, который вы хотите дать сторонам вашего пятиугольника, линия (ab) Рис. 2
- С помощью транспортира остановившись в точке «a «И слева найдите угол 108 °, проведите линию между буквой« a »и точкой пересечения с найденным углом и отметьте на ней размер, выбранный для сторон пятиугольника. (линия ac) рис.3
- Наклонитесь вправо на точку б проделайте ту же процедуру, что и выше, и найдите другую сторону (линия bd) рис. 4
- Затем опирайтесь на точку «c», всегда ища угол 108 °, и нарисуйте (линию се) рис.5.
- Наконец, соедините выделенные точки, составляющие недостающую сторону. Он должен автоматически иметь угол 108 °. Рис. 6
Эта геометрическая фигура имеет более технические и точные формы обводки, но здесь я объясню вам это простым способом, используя только линейки и / или квадраты и транспортир.
Успех построения вашей призмы будет зависеть от точности начертания ее оснований.
А точность построения вашей пятиугольной базы будет зависеть от ваших навыков и знания инструментов измерения, которые я предлагаю.
След призмы
- Нарисуйте длинную прямую линию, которая послужит основой для начала мазка.
- На этой линии отметьте размер (L) пять раз один за другим.
- Перпендикулярно каждой точке нарисуйте вертикальные линии, представляющие края с высотой (h).
- Соедините все точки прямой линией, и вы получите прямоугольник, разделенный на пять равных и параллельных секций, которые представляют каждую из боковых сторон призмы.
- На прямоугольной или центральной грани, или на той, что вы предпочитаете, нарисуйте или добавьте пятиугольное основание как сверху, так и снизу. Это необходимо сделать сначала и на основе этого нарисовать призму.
- Добавьте выступы со всех сторон боковых граней, кроме одной. Эти вкладки помогут вам собрать призму.
- Обрежьте и нанесите клей на ресницы, выделите все линии, чтобы дать им небольшой разрыв и облегчить сгибание краев.
Содержание статьи соответствует нашим принципам редакционная этика. Чтобы сообщить об ошибке, нажмите здесь.
-
Вы здесь:
- Главная
- Правильная пятиугольная призма
Правильная пятиугольная призма
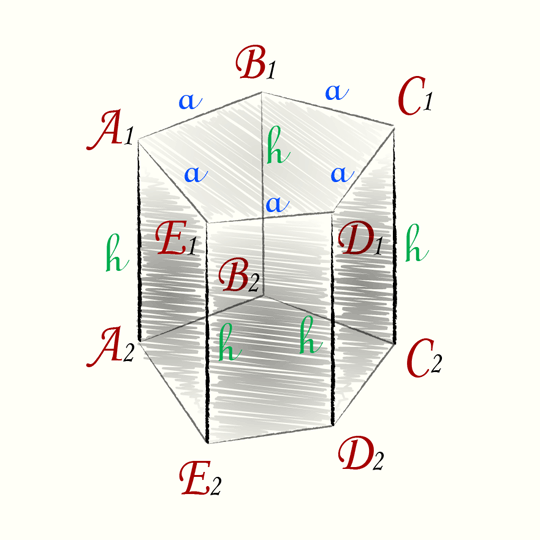
Пятиугольная призма — это многогранник, две грани которого являются равными пятиугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими пятиугольниками.
Правильная пятиугольная призма — это пятиугольная призма у которой основания правильные пятиугольники (все стороны которых равны, углы между сторонами основания составляют 108 градусов), а боковые грани прямоугольники.
Основания призмы являются равными правильными пятиугольниками.
Боковые грани призмы являются прямоугольниками.
Боковые рёбра призмы параллельны и равны.
Размеры призмы можно выразить через длину стороны a и высоту h.
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
Формула площади поверхности пятиугольной призмы:
Объём призмы равен произведению её высоты на площадь основания.
Формула объема правильной пятиугольной призмы:
Правильная пятиугольная призма может быть вписана в цилиндр.
Формула радиуса цилиндра вписанной пятиугольной призмы:
Двойственным многогранником прямой призмы является бипирамида.
Исторически понятие «призма» возникло из латыни и означало — нечто отпиленное.
Анимация демонстрирует как две параллельные плоскости отрезая лишнее формируют два основания призмы. Из одной заготовки можно получить как правильную призму, так и наклонную призму.
Геометрические размеры готовой призмы (мм):
Длина = 80
Ширина = 76
Высота = 50
Геометрические размеры готовой призмы (мм):
Длина = 68
Ширина = 65
Высота = 72
Геометрические размеры готовой призмы (мм):
Длина = 55
Ширина = 52
Высота = 93
посмотреть другие призмы
Популярное
Как собирать многогранники без клея?
До сих пор мы активно применяли для сборки многогранников из наборов «Волшебные грани» клей. Более того, настоятельно рекомендовали применять именно клей Супер-ПВА.
Есть ли…
Миры Ричарда Суини
Молодой британский дизайнер Ричард Суини (Richard Sweeney) создает удивительные скульптуры из…
Куб Принца Руперта
В выпуске 25 «Волшебных граней» мы обратили взор читателя на то, что разрезая куб плоскостью, мы получаем в точке разреза сечение, имеющее форму…
Площадь правильной пятиугольной призмы
Правильная пятиугольная призма — это прямая призма в основании которой лежит правильный пятиугольник.
Площадь правильной пятиугольной призмы
Как мы видим — призма имеет два основания, эти основания правильные пятиугольники со стороной a, и пять боковых сторон, которые представляют из себя прямоугольники со сторонами a и h
Таким образом площадь правильной пятиугольной призмы складывается из двух площадей оснований и пяти площадей боковых граней.
[ S_{призмы} = 2S_{осн} + 5S_{бок} ]
Подставим сюда формулу площади прямоугольника и формулу площади правильного пятиугольника и получим:
[ S_{призмы} = 2frac{5}{2} a sqrt{bigg(frac{a}{2 sin(π/5)}bigg)^2-frac{a^2}{4}} + 5ah ]
или
[ S_{призмы} = 5aBigg(sqrt{bigg(frac{a}{2 sin(π/5)}bigg)^2-frac{a^2}{4}} + hBigg) ]
Вычислить, найти площадь правильной пятиугольной призмы по формуле (3)
Площадь правильной пятиугольной призмы |
стр. 333 |
|---|