From Wikipedia, the free encyclopedia
Quadrature of the Parabola (Greek: Τετραγωνισμὸς παραβολῆς) is a treatise on geometry, written by Archimedes in the 3rd century BC and addressed to his Alexandrian acquaintance Dositheus. It contains 24 propositions regarding parabolas, culminating in two proofs showing that the area of a parabolic segment (the region enclosed by a parabola and a line) is 
It is one of the best-known works of Archimedes, in particular for its ingenious use of the method of exhaustion and in the second part of a geometric series. Archimedes dissects the area into infinitely many triangles whose areas form a geometric progression.[1] He then computes the sum of the resulting geometric series, and proves that this is the area of the parabolic segment. This represents the most sophisticated use of a reductio ad absurdum argument in ancient Greek mathematics, and Archimedes’ solution remained unsurpassed until the development of integral calculus in the 17th century, being succeeded by Cavalieri’s quadrature formula.[2]
Main theorem[edit]
A parabolic segment is the region bounded by a parabola and line. To find the area of a parabolic segment, Archimedes considers a certain inscribed triangle. The base of this triangle is the given chord of the parabola, and the third vertex is the point on the parabola such that the tangent to the parabola at that point is parallel to the chord. Proposition 1 of the work states that a line from the third vertex drawn parallel to the axis divides the chord into equal segments. The main theorem claims that the area of the parabolic segment is 
Structure of the text[edit]
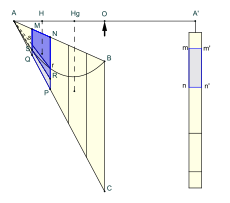
Archimedes’ first proof of the area of a parabolic segment.
Conic sections such as the parabola were already well known in Archimedes’ time thanks to Menaechmus a century earlier. However, before the advent of the differential and integral calculus, there were no easy means to find the area of a conic section. Archimedes provides the first attested solution to this problem by focusing specifically on the area bounded by a parabola and a chord.[3]
Archimedes gives two proofs of the main theorem: one using abstract mechanics and the other one by pure geometry. In the first proof, Archimedes considers a lever in equilibrium under the action of gravity, with weighted segments of a parabola and a triangle suspended along the arms of a lever at specific distances from the fulcrum.[4] When the center of gravity of the triangle is known, the equilibrium of the lever yields the area of the parabola in terms of the area of the triangle which has the same base and equal height.[5] Archimedes here deviates from the procedure found in On the Equilibrium of Planes in that he has the centers of gravity at a level below that of the balance.[6] The second and more famous proof uses pure geometry, particularly the sum of a geometric series.
Of the twenty-four propositions, the first three are quoted without proof from Euclid’s Elements of Conics (a lost work by Euclid on conic sections). Propositions 4 and 5 establish elementary properties of the parabola. Propositions 6–17 give the mechanical proof of the main theorem; propositions 18–24 present the geometric proof.
Geometric proof[edit]
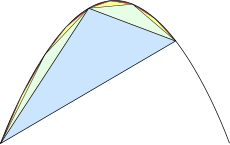
Archimedes’ second proof dissects the area using an arbitrary number of triangles.
Dissection of the parabolic segment[edit]
The main idea of the proof is the dissection of the parabolic segment into infinitely many triangles, as shown in the figure to the right. Each of these triangles is inscribed in its own parabolic segment in the same way that the blue triangle is inscribed in the large segment.
Areas of the triangles[edit]
In propositions eighteen through twenty-one, Archimedes proves that the area of each green triangle is 



Following the same argument, each of the 






Here T represents the area of the large blue triangle, the second term represents the total area of the two green triangles, the third term represents the total area of the four yellow triangles, and so forth. This simplifies to give
Sum of the series[edit]
Archimedes’ proof that 1/4 + 1/16 + 1/64 + ⋯ = 1/3
To complete the proof, Archimedes shows that
The formula above is a geometric series—each successive term is one fourth of the previous term. In modern mathematics, that formula is a special case of the sum formula for a geometric series.
Archimedes evaluates the sum using an entirely geometric method,[8] illustrated in the adjacent picture. This picture shows a unit square which has been dissected into an infinity of smaller squares. Each successive purple square has one fourth the area of the previous square, with the total purple area being the sum
However, the purple squares are congruent to either set of yellow squares, and so cover 


See also[edit]
- History of calculus
Notes[edit]
Further reading[edit]
- Ajose, Sunday and Roger Nelsen (June 1994). «Proof without Words: Geometric Series». Mathematics Magazine. 67 (3): 230. doi:10.2307/2690617. JSTOR 2690617.
- Ancora, Luciano (2014). «Quadrature of the parabola with the square pyramidal number». Archimede. 66 (3).
- Bressoud, David M. (2006). A Radical Approach to Real Analysis (2nd ed.). Mathematical Association of America. ISBN 0-88385-747-2..
- Dijksterhuis, E.J. (1987) «Archimedes», Princeton U. Press ISBN 0-691-08421-1
- Edwards Jr., C. H. (1994). The Historical Development of the Calculus (3rd ed.). Springer. ISBN 0-387-94313-7..
- Heath, Thomas L. (2011). The Works of Archimedes (2nd ed.). CreateSpace. ISBN 978-1-4637-4473-1.
- Simmons, George F. (2007). Calculus Gems. Mathematical Association of America. ISBN 978-0-88385-561-4..
- Stein, Sherman K. (1999). Archimedes: What Did He Do Besides Cry Eureka?. Mathematical Association of America. ISBN 0-88385-718-9.
- Stillwell, John (2004). Mathematics and its History (2nd ed.). Springer. ISBN 0-387-95336-1..
- Swain, Gordon and Thomas Dence (April 1998). «Archimedes’ Quadrature of the Parabola Revisited». Mathematics Magazine. 71 (2): 123–30. doi:10.2307/2691014. JSTOR 2691014.
- Wilson, Alistair Macintosh (1995). The Infinite in the Finite. Oxford University Press. ISBN 0-19-853950-9..
External links[edit]
Look up quadrature in Wiktionary, the free dictionary.
- Casselman, Bill. «Archimedes’ quadrature of the parabola». Archived from the original on 2012-02-04. Full text, as translated by T.L. Heath.
- Xavier University Department of Mathematics and Computer Science. «Archimedes of Syracuse». Archived from the original on 2016-01-13.. Text of propositions 1–3 and 20–24, with commentary.
- http://planetmath.org/ArchimedesCalculus

Квадратура параболы (Греческий : Τετραγωνισμὸς παραβολῆς) — это трактат по геометрии, написанный Архимедом в III веке до нашей эры. Написанная как письмо его другу, работа представляет 24 предложения относительно парабол, кульминацией которых является доказательство того, что площадь параболического сегмента (область, ограниченная параболой и линией ) составляет 4/3 от некоторого вписанного треугольника.
В операторе проблемы использовался метод исчерпания. Архимед мог разрезать местность на бесконечное множество треугольников, площади которых образуют геометрическую прогрессию. Он вычисляет сумму результирующего геометрического ряда и доказывает, что это площадь параболического сегмента. Это представляет собой наиболее изощренное использование метода исчерпания в древней математике и оставалось непревзойденным до развития интегрального исчисления в 17 веке, на смену которому пришла квадратурная формула Кавальери.
Содержание
- 1 Основная теорема
- 2 Структура текста
- 3 Геометрическое доказательство
- 3.1 Рассечение параболического отрезка
- 3.2 Площади треугольников
- 3.3 Сумма ряда
- 4 См. Также
- 5 Примечания
- 6 Дополнительная литература
- 7 Внешние ссылки
Основная теорема

A параболический сегмент — это область, ограниченная параболой и линия. Чтобы найти площадь параболического сегмента, Архимед рассматривает некий вписанный треугольник. Основание этого треугольника — заданная хорда параболы, а третья вершина — это точка на параболе, касательная к параболе в этой точке параллельна хорде. Согласно предложению 1 (Квадратура параболы), прямая из третьей вершины, проведенная параллельно оси, делит хорду на равные отрезки. Основная теорема утверждает, что площадь параболического сегмента равна 4/3 площади вписанного треугольника.
Структура текста
Архимед дает два доказательства основной теоремы. В первом используется абстрактная механика, причем Архимед утверждает, что вес сегмента уравновесит вес треугольника, когда он помещен на соответствующий рычаг. Второе, более известное доказательство использует чистую геометрию, в частности метод исчерпания.
. Из двадцати четырех предложений первые три цитируются без доказательства из «Элементов коник» Евклида (a утерянная работа Евклида на конических сечениях ). Предложения четвертый и пятый устанавливают элементарные свойства параболы; предложения с шестого по семнадцатый дают механическое доказательство основной теоремы; предложения с восемнадцатого по двадцать четвертый представляют геометрическое доказательство.
Геометрическое доказательство
Разрез параболического сегмента

Основная идея доказательства — разрезание параболического сегмента. параболический сегмент на бесконечное количество треугольников, как показано на рисунке справа. Каждый из этих треугольников вписан в свой параболический сегмент так же, как синий треугольник вписан в большой сегмент.
Площади треугольников
В предложениях с восемнадцатого по двадцать один Архимед доказывает, что площадь каждого зеленого треугольника составляет одну восьмую площади синего треугольника. С современной точки зрения, это потому, что зеленый треугольник имеет половину ширины и четверть высоты:
В более широком смысле, каждый из желтых треугольников имеет одну восьмую площади зеленого треугольника, каждый из красных треугольников имеет одну восьмую площади желтого треугольника и так далее. Используя метод истощения, следует, что общая площадь параболического сегмента определяется как
- Площадь = T + 2 (T
+ 4 (T 8 2) + 8 (T 8 3) + ⋯. { displaystyle { text {Area}} ; = ; T , + , 2 left ({ frac {T} {8}} right) , + , 4 left ({ frac {T} {8 ^ {2}}} right) , + , 8 left ({ frac {T} {8 ^ {3}}} right) , + , cdots.}
Здесь T представляет площадь большого синего треугольника, второй член представляет общую площадь двух зеленых треугольников, третий член представляет общую площадь четырех желтых треугольников и так далее. Это упрощает получение
- Площадь = (1 + 1 4 + 1 16 + 1 64 + ⋯) T. { displaystyle { text {Area}} ; = ; left (1 , + , { frac {1} {4}} , + , { frac {1} {16}} , + , { frac {1} {64}} , + , cdots right) T.}
Сумма ряда

Чтобы завершить доказательство, Архимед показывает, что
- 1 + 1 4 + 1 16 + 1 64 + ⋯ = 4 3. { displaystyle 1 , + , { frac {1} {4}} , + , { frac {1} {16}} , + , { frac {1} {64}} , + , cdots ; = ; { frac {4} {3}}.}
Вышеупомянутая формула представляет собой геометрический ряд — каждый последующий член составляет одну четверть предыдущего члена. В современной математике эта формула является частным случаем формулы суммы для геометрического ряда..
Архимед вычисляет сумму, используя полностью геометрический метод, показанный на рисунке рядом. На этой картинке изображен единичный квадрат, разбитый на бесконечное множество меньших квадратов. Каждый последующий фиолетовый квадрат имеет одну четвертую площадь предыдущего квадрата, а общая фиолетовая площадь равна сумме
- 1 4 + 1 16 + 1 64 + ⋯. { displaystyle { frac {1} {4}} , + , { frac {1} {16}} , + , { frac {1} {64}} , + , cdots.}
Однако фиолетовые квадраты соответствуют любому набору желтых квадратов и поэтому покрывают 1/3 площади единичного квадрата. Отсюда следует, что сумма приведенного выше ряда составляет 4/3.
См. Также
| Викискладе есть материалы, относящиеся к Квадратуре параболы . |
- Истории исчисления
Примечания
Дополнительная литература
- Ajose, Сандей и Роджер Нельсен (июнь 1994 г.). «Доказательство без слов: геометрические ряды». Математический журнал. 67 (3): 230. doi : 10.2307 / 2690617. JSTOR 2690617.
- Анкора, Лучано (2014). «Квадратура параболы с квадратным пирамидальным числом». Архимед. 66 (3).
- Брессуд, Дэвид М. (2006). Радикальный подход к реальному анализу (2-е изд.). Математическая ассоциация Америки. ISBN 0-88385-747-2 ..
- Dijksterhuis, E.J. (1987) «Archimedes», Princeton U. Press ISBN 0-691-08421-1
- Edwards Jr., C.H. (1994). Историческое развитие математического анализа (3-е изд.). Springer. ISBN 0-387-94313-7 ..
- Хит, Томас Л. (2011). Сочинения Архимеда (2-е изд.). CreateSpace. ISBN 978-1-4637-4473-1 .
- Симмонс, Джордж Ф. (2007). Камни исчисления. Математическая ассоциация Америки. ISBN 978-0-88385-561-4 ..
- Штейн, Шерман К. (1999). Архимед: Чем он занимался, кроме плачущей Эврики?. Математическая ассоциация Америки. ISBN 0-88385-718-9 .
- Стиллвелл, Джон (2004). Математика и ее история (2-е изд.). Springer. ISBN 0-387-95336-1 ..
- Суэйн, Гордон и Томас Денс (апрель 1998 г.). «Квадратура Архимеда параболы снова и снова». Математический журнал. 71 (2): 123–30. doi : 10.2307 / 2691014. JSTOR 2691014.
- Уилсон, Алистер Макинтош (1995). Бесконечное в конечном. Издательство Оксфордского университета. ISBN 0-19-853950-9 ..
Внешние ссылки
| Найдите справочник в Wiktionary, бесплатном словаре. |
- Кассельман, Билл. «Квадратура Архимеда параболы».Полный текст в переводе Т.Л. Хит.
- Университет Ксавьера Департамент математики и информатики. «Архимед Сиракузский».Текст предложений 1–3 и 20–24 с комментариями.
- http://planetmath.org/ArchimedesCalculus
Квадратура Параболы ( греч . Τετραγωνισμὸς παραβολῆς ) — это трактат по геометрии , написанный Архимедом в 3 веке до нашей эры и адресованный его александрийскому знакомому Досифею. Он содержит 24 утверждения относительно парабол , кульминацией которых являются два доказательства, показывающих, что площадь параболического сегмента (область, ограниченная параболой и линией ) равна 4/3 площади определенного вписанного треугольника .
Это одна из самых известных работ Архимеда, в особенности вторая часть за гениальное использование метода истощения . Архимед мог разрезать эту область на бесконечное количество треугольников , площади которых образуют геометрическую прогрессию . Затем он вычисляет сумму полученного геометрического ряда и доказывает, что это площадь параболического сегмента. Это представляет собой наиболее изощренное использование аргумента reductio ad absurdum в древнегреческой математике , и решение Архимеда оставалось непревзойденным до развития интегрального исчисления в 17 веке, на смену которому пришла квадратурная формула Кавальери .
Основная теорема
Параболический сегмент представляет собой область , ограниченную параболы и линии. Чтобы найти площадь параболического сегмента, Архимед рассматривает некий вписанный треугольник. Основание этого треугольника — заданная хорда параболы, а третья вершина — это точка параболы, касательная к параболе в этой точке параллельна хорде. Предложение 1 работы гласит, что линия от третьей вершины, проведенная параллельно оси, делит хорду на равные отрезки. Основная теорема утверждает, что площадь параболического отрезка равна 4/3 площади вписанного треугольника.
Структура текста
Первое доказательство Архимеда использует принцип рычага для определения площади параболического сегмента.
Конические сечения, такие как парабола, были хорошо известны еще во времена Архимеда благодаря Менехму столетием раньше. Однако до появления дифференциального и интегрального исчислений не было простых способов найти площадь конического сечения. Архимед предоставляет первое подтвержденное решение этой проблемы, уделяя особое внимание области, ограниченной параболой и хордой.
Архимед приводит два доказательства основной теоремы: одно с использованием абстрактной механики, а другое с помощью чистой геометрии. В первом доказательстве Архимед рассматривает рычаг, находящийся в равновесии под действием силы тяжести, с взвешенными сегментами параболы и треугольником, подвешенными вдоль плеч рычага на определенных расстояниях от точки опоры. Когда центр тяжести треугольника известен, равновесие рычага дает площадь параболы в терминах площади треугольника, который имеет то же основание и одинаковую высоту. Здесь Архимед отклоняется от процедуры, описанной в «Равновесии планов», в том, что он имеет центры тяжести на уровне ниже, чем баланс. Второе и более известное доказательство использует чистую геометрию, особенно метод исчерпания .
Из двадцати четырех предложений, первые три указаны без доказательства от Евклида «s Элементов коников (утраченной работы Евклида на конических сечениях ). Предложения 4 и 5 устанавливают элементарные свойства параболы. Предложения 6-17 дают механическое доказательство основной теоремы; Предложения 18-24 представляют собой геометрическое доказательство.
Геометрическое доказательство
Второе доказательство Архимеда разбивает параболический отрезок на произвольное количество треугольников.
Рассечение параболического сегмента
Основная идея доказательства — разбиение параболического отрезка на бесконечное количество треугольников, как показано на рисунке справа. Каждый из этих треугольников вписан в свой собственный параболический сегмент так же, как синий треугольник вписан в большой сегмент.
Площади треугольников
В предложениях с восемнадцатого по двадцать один Архимед доказывает, что площадь каждого зеленого треугольника составляет одну восьмую площади синего треугольника. С современной точки зрения, это потому, что зеленый треугольник имеет половину ширины и четверть высоты:
В более широком смысле, каждый из желтых треугольников имеет одну восьмую площади зеленого треугольника, каждый из красных треугольников имеет одну восьмую площади желтого треугольника и так далее. Используя метод исчерпания , следует, что общая площадь параболического сегмента определяется выражением
Здесь T представляет площадь большого синего треугольника, второй член представляет общую площадь двух зеленых треугольников, третий член представляет общую площадь четырех желтых треугольников и так далее. Это упрощает предоставление
Сумма серии
Доказательство Архимеда, что 1/4 + 1/16 + 1/64 + … = 1/3
Чтобы завершить доказательство, Архимед показывает, что
Приведенная выше формула представляет собой геометрический ряд: каждый последующий член составляет одну четверть предыдущего члена. В современной математике эта формула является частным случаем формулы суммы для геометрического ряда .
Архимед вычисляет сумму, используя полностью геометрический метод, показанный на рисунке рядом. На этой картинке изображен единичный квадрат, разбитый на бесконечное множество меньших квадратов. Каждый последующий фиолетовый квадрат имеет одну четвертую площадь предыдущего квадрата, а общая фиолетовая площадь является суммой.
Однако фиолетовые квадраты соответствуют любому набору желтых квадратов и поэтому покрывают 1/3 площади единичного квадрата. Отсюда следует, что сумма приведенного выше ряда составляет 4/3 (так как 1 + 1/3 = 4/3).
Смотрите также
- История исчисления
Примечания
дальнейшее чтение
- Аджосе, Сандей и Роджер Нельсен (июнь 1994 г.). «Доказательство без слов: геометрические ряды». Математический журнал . 67 (3): 230. DOI : 10,2307 / 2690617 . JSTOR 2690617 .
- Анкора, Лучано (2014). «Квадратура параболы с квадратным пирамидальным числом» . Архимед . 66 (3).
- Брессуд, Дэвид М. (2006). Радикальный подход к реальному анализу (2-е изд.). Математическая ассоциация Америки . ISBN 0-88385-747-2..
- Dijksterhuis, EJ (1987) «Archimedes», Princeton U. Press ISBN 0-691-08421-1
- Эдвардс-младший, CH (1994). Историческое развитие математического анализа (3-е изд.). Springer. ISBN 0-387-94313-7..
- Хит, Томас Л. (2011). Сочинения Архимеда (2-е изд.). CreateSpace. ISBN 978-1-4637-4473-1.
- Симмонс, Джордж Ф. (2007). Исчисление драгоценных камней . Математическая ассоциация Америки. ISBN 978-0-88385-561-4..
- Штейн, Шерман К. (1999). Архимед: Чем он занимался помимо Cry Eureka? . Математическая ассоциация Америки. ISBN 0-88385-718-9.
- Стиллвелл, Джон (2004). Математика и ее история (2-е изд.). Springer. ISBN 0-387-95336-1..
- Суэйн, Гордон и Томас Денс (апрель 1998 г.). «Квадратура Параболы Архимеда». Математический журнал . 71 (2): 123–30. DOI : 10.2307 / 2691014 . JSTOR 2691014 .
- Уилсон, Алистер Макинтош (1995). Бесконечное в конечном . Издательство Оксфордского университета . ISBN 0-19-853950-9..
внешние ссылки
- Кассельман, Билл. «Квадратура Архимеда параболы» . Полный текст в переводе Т.Л. Хита.
- Университет Ксавьера, факультет математики и информатики. «Архимед Сиракузский» . Текст предложений 1–3 и 20–24 с комментариями.
- http://planetmath.org/ArchimedesCalculus









 + 4 (T 8 2) + 8 (T 8 3) + ⋯. { displaystyle { text {Area}} ; = ; T , + , 2 left ({ frac {T} {8}} right) , + , 4 left ({ frac {T} {8 ^ {2}}} right) , + , 8 left ({ frac {T} {8 ^ {3}}} right) , + , cdots.}
+ 4 (T 8 2) + 8 (T 8 3) + ⋯. { displaystyle { text {Area}} ; = ; T , + , 2 left ({ frac {T} {8}} right) , + , 4 left ({ frac {T} {8 ^ {2}}} right) , + , 8 left ({ frac {T} {8 ^ {3}}} right) , + , cdots.}

