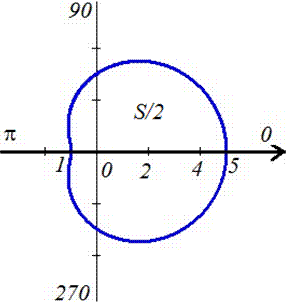
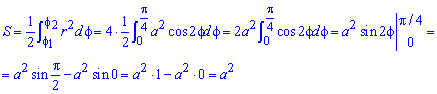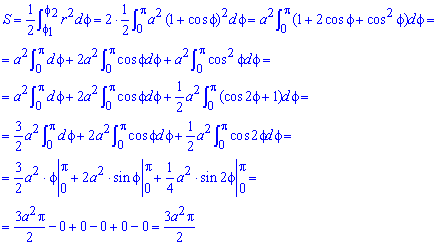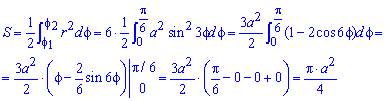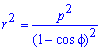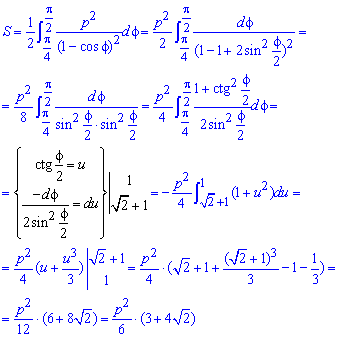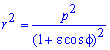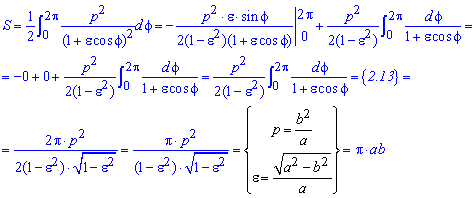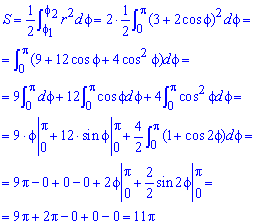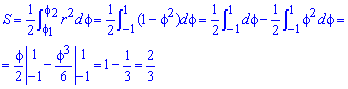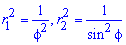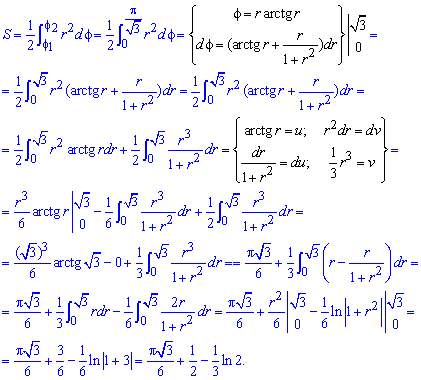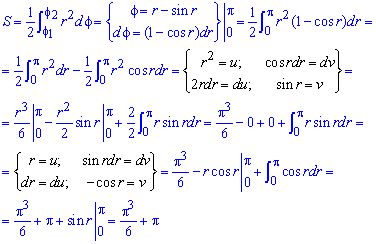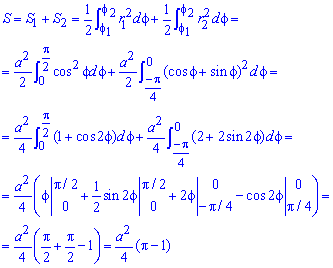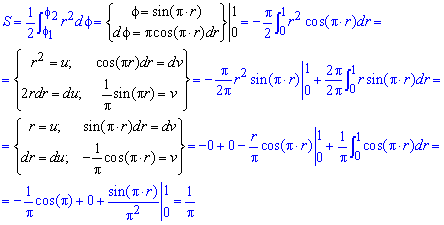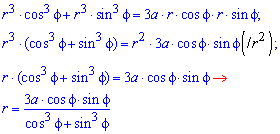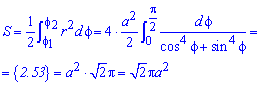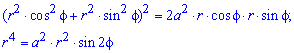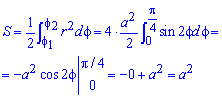Нахождение площади фигуры, ограниченной линиями y=f(x), x=g(y)
В предыдущем разделе, посвященном разбору геометрического смысла определенного интеграла, мы получили ряд формул для вычисления площади криволинейной трапеции:
S ( G ) = ∫ a b f ( x ) d x для непрерывной и неотрицательной функции y = f ( x ) на отрезке [ a ; b ] ,
S ( G ) = — ∫ a b f ( x ) d x для непрерывной и неположительной функции y = f ( x ) на отрезке [ a ; b ] .
Эти формулы применимы для решения относительно простых задач. На деле же нам чаще придется работать с более сложными фигурами. В связи с этим, данный раздел мы посвятим разбору алгоритмов вычисления площади фигур, которые ограничены функциями в явном виде, т.е. как y = f ( x ) или x = g ( y ) .
Формула для вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
Пусть функции y = f 1 ( x ) и y = f 2 ( x ) определены и непрерывны на отрезке [ a ; b ] , причем f 1 ( x ) ≤ f 2 ( x ) для любого значения x из [ a ; b ] . Тогда формула для вычисления площади фигуры G , ограниченной линиями x = a , x = b , y = f 1 ( x ) и y = f 2 ( x ) будет иметь вид S ( G ) = ∫ a b f 2 ( x ) — f 1 ( x ) d x .
Похожая формула будет применима для площади фигуры, ограниченной линиями y = c , y = d , x = g 1 ( y ) и x = g 2 ( y ) : S ( G ) = ∫ c d ( g 2 ( y ) — g 1 ( y ) d y .
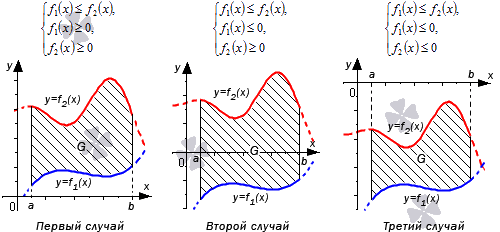
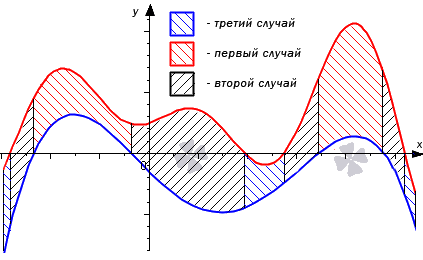
Разберем три случая, для которых формула будет справедлива.
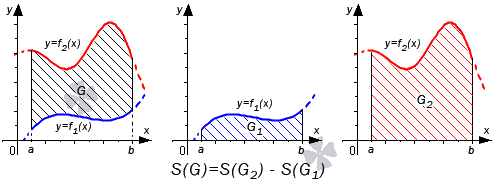
В первом случае, учитывая свойство аддитивности площади, сумма площадей исходной фигуры G и криволинейной трапеции G 1 равна площади фигуры G 2 . Это значит, что
Поэтому, S ( G ) = S ( G 2 ) — S ( G 1 ) = ∫ a b f 2 ( x ) d x — ∫ a b f 1 ( x ) d x = ∫ a b ( f 2 ( x ) — f 1 ( x ) ) d x .
Выполнить последний переход мы можем с использованием третьего свойства определенного интеграла.
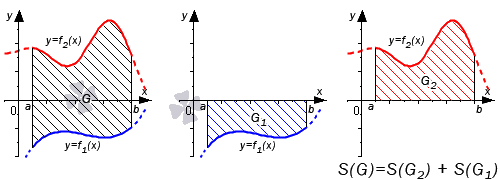
Во втором случае справедливо равенство: S ( G ) = S ( G 2 ) + S ( G 1 ) = ∫ a b f 2 ( x ) d x + — ∫ a b f 1 ( x ) d x = ∫ a b ( f 2 ( x ) — f 1 ( x ) ) d x
Графическая иллюстрация будет иметь вид:
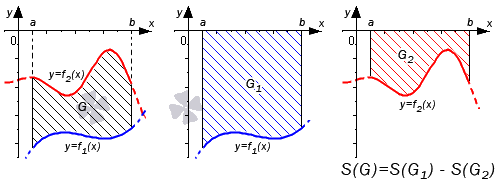
Если обе функции неположительные, получаем: S ( G ) = S ( G 2 ) — S ( G 1 ) = — ∫ a b f 2 ( x ) d x — — ∫ a b f 1 ( x ) d x = ∫ a b ( f 2 ( x ) — f 1 ( x ) ) d x . Графическая иллюстрация будет иметь вид:
Перейдем к рассмотрению общего случая, когда y = f 1 ( x ) и y = f 2 ( x ) пересекают ось O x .
Точки пересечения мы обозначим как x i , i = 1 , 2 , . . . , n — 1 . Эти точки разбивают отрезок [ a ; b ] на n частей x i — 1 ; x i , i = 1 , 2 , . . . , n , где α = x 0 x 1 x 2 . . . x n — 1 x n = b . Фигуру G можно представить объединением фигур G i , i = 1 , 2 , . . . , n . Очевидно, что на своем интервале G i попадает под один из трех рассмотренных ранее случаев, поэтому их площади находятся как S ( G i ) = ∫ x i — 1 x i ( f 2 ( x ) — f 1 ( x ) ) d x , i = 1 , 2 , . . . , n
S ( G ) = ∑ i = 1 n S ( G i ) = ∑ i = 1 n ∫ x i x i f 2 ( x ) — f 1 ( x ) ) d x = = ∫ x 0 x n ( f 2 ( x ) — f ( x ) ) d x = ∫ a b f 2 ( x ) — f 1 ( x ) d x
Последний переход мы можем осуществить с использованием пятого свойства определенного интеграла.
Проиллюстрируем на графике общий случай.
Формулу S ( G ) = ∫ a b f 2 ( x ) — f 1 ( x ) d x можно считать доказанной.
А теперь перейдем к разбору примеров вычисления площади фигур, которые ограничены линиями y = f ( x ) и x = g ( y ) .
Примеры вычисления площади фигуры, ограниченной линиями y=f(x) или x=g(y)
Рассмотрение любого из примеров мы будем начинать с построения графика. Изображение позволит нам представлять сложные фигуры как объединения более простых фигур. Если построение графиков и фигур на них вызывает у вас затруднения, можете изучить раздел об основных элементарных функциях, геометрическом преобразовании графиков функций, а также построению графиков во время исследования функции.
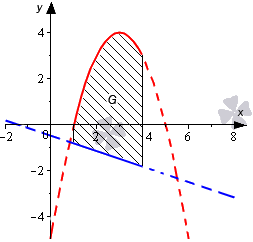
Необходимо определить площадь фигуры, которая ограничена параболой y = — x 2 + 6 x — 5 и прямыми линиями y = — 1 3 x — 1 2 , x = 1 , x = 4 .
Решение
Изобразим линии на графике в декартовой системе координат.
На отрезке [ 1 ; 4 ] график параболы y = — x 2 + 6 x — 5 расположен выше прямой y = — 1 3 x — 1 2 . В связи с этим, для получения ответа используем формулу, полученную ранее, а также способ вычисления определенного интеграла по формуле Ньютона-Лейбница:
S ( G ) = ∫ 1 4 — x 2 + 6 x — 5 — — 1 3 x — 1 2 d x = = ∫ 1 4 — x 2 + 19 3 x — 9 2 d x = — 1 3 x 3 + 19 6 x 2 — 9 2 x 1 4 = = — 1 3 · 4 3 + 19 6 · 4 2 — 9 2 · 4 — — 1 3 · 1 3 + 19 6 · 1 2 — 9 2 · 1 = = — 64 3 + 152 3 — 18 + 1 3 — 19 6 + 9 2 = 13
Ответ: S ( G ) = 13
Рассмотрим более сложный пример.
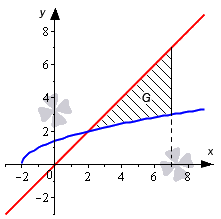
Необходимо вычислить площадь фигуры, которая ограничена линиями y = x + 2 , y = x , x = 7 .
Решение
В данном случае мы имеем только одну прямую линию, расположенную параллельно оси абсцисс. Это x = 7 . Это требует от нас найти второй предел интегрирования самостоятельно.
Построим график и нанесем на него линии, данные в условии задачи.
Имея график перед глазами, мы легко можем определить, что нижним пределом интегрирования будет абсцисса точки пересечения графика прямой y = x и полу параболы y = x + 2 . Для нахождения абсциссы используем равенства:
y = x + 2 О Д З : x ≥ — 2 x 2 = x + 2 2 x 2 — x — 2 = 0 D = ( — 1 ) 2 — 4 · 1 · ( — 2 ) = 9 x 1 = 1 + 9 2 = 2 ∈ О Д З x 2 = 1 — 9 2 = — 1 ∉ О Д З
Получается, что абсциссой точки пересечения является x = 2 .
Обращаем ваше внимание на тот факт, что в общем примере на чертеже линии y = x + 2 , y = x пересекаются в точке ( 2 ; 2 ) , поэтому такие подробные вычисления могут показаться излишними. Мы привели здесь такое подробное решение только потому, что в более сложных случаях решение может быть не таким очевидным. Это значит, что координаты пересечения линий лучше всегда вычислять аналитически.
На интервале [ 2 ; 7 ] график функции y = x расположен выше графика функции y = x + 2 . Применим формулу для вычисления площади:
S ( G ) = ∫ 2 7 ( x — x + 2 ) d x = x 2 2 — 2 3 · ( x + 2 ) 3 2 2 7 = = 7 2 2 — 2 3 · ( 7 + 2 ) 3 2 — 2 2 2 — 2 3 · 2 + 2 3 2 = = 49 2 — 18 — 2 + 16 3 = 59 6
Ответ: S ( G ) = 59 6
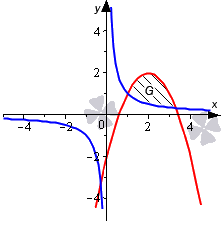
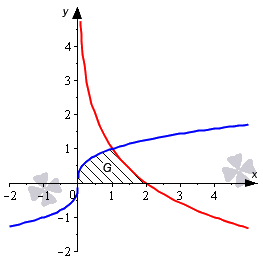
Необходимо вычислить площадь фигуры, которая ограничена графиками функций y = 1 x и y = — x 2 + 4 x — 2 .
Решение
Нанесем линии на график.
Определимся с пределами интегрирования. Для этого определим координаты точек пересечения линий, приравняв выражения 1 x и — x 2 + 4 x — 2 . При условии, что x не равно нулю, равенство 1 x = — x 2 + 4 x — 2 становится эквивалентным уравнению третьей степени — x 3 + 4 x 2 — 2 x — 1 = 0 с целыми коэффициентами. Освежить в памяти алгоритм по решению таких уравнений мы можете, обратившись к разделу «Решение кубических уравнений».
Корнем этого уравнения является х = 1 : — 1 3 + 4 · 1 2 — 2 · 1 — 1 = 0 .
Разделив выражение — x 3 + 4 x 2 — 2 x — 1 на двучлен x — 1 , получаем: — x 3 + 4 x 2 — 2 x — 1 ⇔ — ( x — 1 ) ( x 2 — 3 x — 1 ) = 0
Оставшиеся корни мы можем найти из уравнения x 2 — 3 x — 1 = 0 :
x 2 — 3 x — 1 = 0 D = ( — 3 ) 2 — 4 · 1 · ( — 1 ) = 13 x 1 = 3 + 13 2 ≈ 3 . 3 ; x 2 = 3 — 13 2 ≈ — 0 . 3
Мы нашли интервал x ∈ 1 ; 3 + 13 2 , на котором фигура G заключена выше синей и ниже красной линии. Это помогает нам определить площадь фигуры:
S ( G ) = ∫ 1 3 + 13 2 — x 2 + 4 x — 2 — 1 x d x = — x 3 3 + 2 x 2 — 2 x — ln x 1 3 + 13 2 = = — 3 + 13 2 3 3 + 2 · 3 + 13 2 2 — 2 · 3 + 13 2 — ln 3 + 13 2 — — — 1 3 3 + 2 · 1 2 — 2 · 1 — ln 1 = 7 + 13 3 — ln 3 + 13 2
Ответ: S ( G ) = 7 + 13 3 — ln 3 + 13 2
Необходимо вычислить площадь фигуры, которая ограничена кривыми y = x 3 , y = — log 2 x + 1 и осью абсцисс.
Решение
Нанесем все линии на график. Мы можем получить график функции y = — log 2 x + 1 из графика y = log 2 x , если расположим его симметрично относительно оси абсцисс и поднимем на одну единицу вверх. Уравнение оси абсцисс у = 0 .
Обозначим точки пересечения линий.
Как видно из рисунка, графики функций y = x 3 и y = 0 пересекаются в точке ( 0 ; 0 ) . Так получается потому, что х = 0 является единственным действительным корнем уравнения x 3 = 0 .
x = 2 является единственным корнем уравнения — log 2 x + 1 = 0 , поэтому графики функций y = — log 2 x + 1 и y = 0 пересекаются в точке ( 2 ; 0 ) .
x = 1 является единственным корнем уравнения x 3 = — log 2 x + 1 . В связи с этим графики функций y = x 3 и y = — log 2 x + 1 пересекаются в точке ( 1 ; 1 ) . Последнее утверждение может быть неочевидным, но уравнение x 3 = — log 2 x + 1 не может иметь более одного корня, так как функция y = x 3 является строго возрастающей, а функция y = — log 2 x + 1 строго убывающей.
Дальнейшее решение предполагает несколько вариантов.
Вариант №1
Фигуру G мы можем представить как сумму двух криволинейных трапеций, расположенных выше оси абсцисс, первая из которых располагается ниже средней линии на отрезке x ∈ 0 ; 1 , а вторая ниже красной линии на отрезке x ∈ 1 ; 2 . Это значит, что площадь будет равна S ( G ) = ∫ 0 1 x 3 d x + ∫ 1 2 ( — log 2 x + 1 ) d x .
Вариант №2
Фигуру G можно представить как разность двух фигур, первая из которых расположена выше оси абсцисс и ниже синей линии на отрезке x ∈ 0 ; 2 , а вторая между красной и синей линиями на отрезке x ∈ 1 ; 2 . Это позволяет нам найти площадь следующим образом:
S ( G ) = ∫ 0 2 x 3 d x — ∫ 1 2 x 3 — ( — log 2 x + 1 ) d x
В этом случае для нахождения площади придется использовать формулу вида S ( G ) = ∫ c d ( g 2 ( y ) — g 1 ( y ) ) d y . Фактически, линии, которые ограничивают фигуру, можно представить в виде функций от аргумента y .
Разрешим уравнения y = x 3 и — log 2 x + 1 относительно x :
y = x 3 ⇒ x = y 3 y = — log 2 x + 1 ⇒ log 2 x = 1 — y ⇒ x = 2 1 — y
Получим искомую площадь:
S ( G ) = ∫ 0 1 ( 2 1 — y — y 3 ) d y = — 2 1 — y ln 2 — y 4 4 0 1 = = — 2 1 — 1 ln 2 — 1 4 4 — — 2 1 — 0 ln 2 — 0 4 4 = — 1 ln 2 — 1 4 + 2 ln 2 = 1 ln 2 — 1 4
Ответ: S ( G ) = 1 ln 2 — 1 4
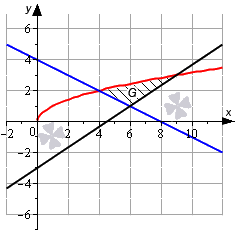
Необходимо вычислить площадь фигуры, которая ограничена линиями y = x , y = 2 3 x — 3 , y = — 1 2 x + 4 .
Решение
Красной линией нанесем на график линию, заданную функцией y = x . Синим цветом нанесем линию y = — 1 2 x + 4 , черным цветом обозначим линию y = 2 3 x — 3 .
Отметим точки пересечения.
Найдем точки пересечения графиков функций y = x и y = — 1 2 x + 4 :
x = — 1 2 x + 4 О Д З : x ≥ 0 x = — 1 2 x + 4 2 ⇒ x = 1 4 x 2 — 4 x + 16 ⇔ x 2 — 20 x + 64 = 0 D = ( — 20 ) 2 — 4 · 1 · 64 = 144 x 1 = 20 + 144 2 = 16 ; x 2 = 20 — 144 2 = 4 П р о в е р к а : x 1 = 16 = 4 , — 1 2 x 1 + 4 = — 1 2 · 16 + 4 = — 4 ⇒ x 1 = 16 н е я в л я е т с я р е ш е н и е м у р а в н е н и я x 2 = 4 = 2 , — 1 2 x 2 + 4 = — 1 2 · 4 + 4 = 2 ⇒ x 2 = 4 я в л я е т с я р е ш е н и е м у р а в н и н и я ⇒ ( 4 ; 2 ) т о ч к а п е р е с е ч е н и я y = x и y = — 1 2 x + 4
Найдем точку пересечения графиков функций y = x и y = 2 3 x — 3 :
x = 2 3 x — 3 О Д З : x ≥ 0 x = 2 3 x — 3 2 ⇔ x = 4 9 x 2 — 4 x + 9 ⇔ 4 x 2 — 45 x + 81 = 0 D = ( — 45 ) 2 — 4 · 4 · 81 = 729 x 1 = 45 + 729 8 = 9 , x 2 45 — 729 8 = 9 4 П р о в е р к а : x 1 = 9 = 3 , 2 3 x 1 — 3 = 2 3 · 9 — 3 = 3 ⇒ x 1 = 9 я в л я е т с я р е ш е н и е м у р а в н е н и я ⇒ ( 9 ; 3 ) т о ч к а п е р е с е ч а н и я y = x и y = 2 3 x — 3 x 2 = 9 4 = 3 2 , 2 3 x 1 — 3 = 2 3 · 9 4 — 3 = — 3 2 ⇒ x 2 = 9 4 н е я в л я е т с я р е ш е н и е м у р а в н е н и я
Найдем точку пересечения линий y = — 1 2 x + 4 и y = 2 3 x — 3 :
— 1 2 x + 4 = 2 3 x — 3 ⇔ — 3 x + 24 = 4 x — 18 ⇔ 7 x = 42 ⇔ x = 6 — 1 2 · 6 + 4 = 2 3 · 6 — 3 = 1 ⇒ ( 6 ; 1 ) т о ч к а п е р е с е ч е н и я y = — 1 2 x + 4 и y = 2 3 x — 3
Дальше мы можем продолжить вычисления двумя способами.
Способ №1
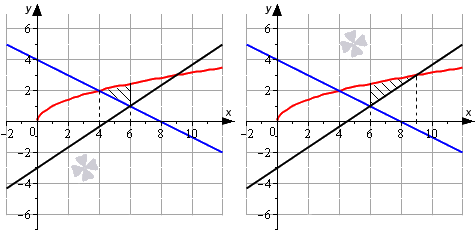
Представим площадь искомой фигуры как сумму площадей отдельных фигур.
Тогда площадь фигуры равна:
S ( G ) = ∫ 4 6 x — — 1 2 x + 4 d x + ∫ 6 9 x — 2 3 x — 3 d x = = 2 3 x 3 2 + x 2 4 — 4 x 4 6 + 2 3 x 3 2 — x 2 3 + 3 x 6 9 = = 2 3 · 6 3 2 + 6 2 4 — 4 · 6 — 2 3 · 4 3 2 + 4 2 4 — 4 · 4 + + 2 3 · 9 3 2 — 9 2 3 + 3 · 9 — 2 3 · 6 3 2 — 6 2 3 + 3 · 6 = = — 25 3 + 4 6 + — 4 6 + 12 = 11 3
Способ №2
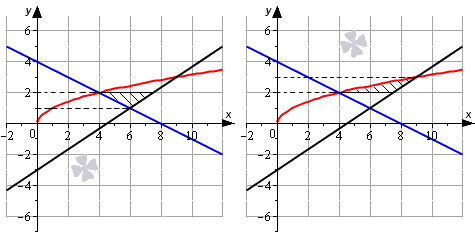
Площадь исходной фигуры можно представить как сумму двух других фигур.
Тогда решим уравнение линии относительно x , а только после этого применим формулу вычисления площади фигуры.
y = x ⇒ x = y 2 к р а с н а я л и н и я y = 2 3 x — 3 ⇒ x = 3 2 y + 9 2 ч е р н а я л и н и я y = — 1 2 x + 4 ⇒ x = — 2 y + 8 с и н я я л и н и я
Таким образом, площадь равна:
S ( G ) = ∫ 1 2 3 2 y + 9 2 — — 2 y + 8 d y + ∫ 2 3 3 2 y + 9 2 — y 2 d y = = ∫ 1 2 7 2 y — 7 2 d y + ∫ 2 3 3 2 y + 9 2 — y 2 d y = = 7 4 y 2 — 7 4 y 1 2 + — y 3 3 + 3 y 2 4 + 9 2 y 2 3 = 7 4 · 2 2 — 7 4 · 2 — 7 4 · 1 2 — 7 4 · 1 + + — 3 3 3 + 3 · 3 2 4 + 9 2 · 3 — — 2 3 3 + 3 · 2 2 4 + 9 2 · 2 = = 7 4 + 23 12 = 11 3
Как видите, значения совпадают.
Ответ: S ( G ) = 11 3
Итоги
Для нахождения площади фигуры, которая ограничена заданными линиями нам необходимо построить линии на плоскости, найти точки их пересечения, применить формулу для нахождения площади. В данном разделе мы рассмотрели наиболее часто встречающиеся варианты задач.
Методы вычисления площади фигуры, ограниченной линиями
- Общие сведения
- Информация об интегралах
- Криволинейные фигуры
- Способы вычисления и рекомендации
- Основной алгоритм
- Примеры решения
- Разновидность параболы
- Гипербола, степенная и прямая
Общие сведения
Вычислить площадь фигуры на плоскости считается довольно простой операцией. Для ее выполнения необходимо знать только формулу. Существенно усложняет задачу фигура, ограниченная прямыми.
Одной из них считается криволинейная трапеция. Ее площадь можно определить только при нахождении значений определенного интеграла.
Операция интегрирования считается довольно сложной, поскольку необходимо знать основные правила. Перед нахождением площади криволинейной трапеции специалисты рекомендуют внимательно изучить и освоить правила интегрирования основных функций.
Разбирается неопределенный интеграл, а затем осуществляется переход к более сложным операциям.
Информация об интегралах
С понятием интеграла связано много направлений научных отраслей. Обозначается он символом «∫». С помощью интеграла открываются большие возможности по быстрому и эффективному нахождению значений следующих величин: площади криволинейной трапеции, объема тела вращения, поверхности, пути при неравномерном движении, массы неоднородного физического тела и так далее.
Упрощенный вариант представления и определения интеграла — сумма бесконечно малых слагаемых. Интеграл бывает нескольких типов: одинарный, двойной, тройной, криволинейный и так далее. Для любого элемента он может быть двух типов:
Операция нахождения первого типа значительно проще второго. Это объясняется тем, что во втором случае следует не только найти первообразную, но и выполнить правильную подстановку значений.
Неопределенным интегралом функции вида f(х) называется такая первообразная функция F(х), производная которой равна подинтегральному выражению. Записывается это таким образом: ∫(f(x)) = F(х) + С.
Последняя величина является константой, поскольку при выполнении операции нахождения производной константа равна 0.
Для нахождения первообразной используется специальная таблица интегралов:
Рисунок 1. Таблица интегралов и их первообразные.
В таблице приведены простые функции. Для нахождения площади фигуры, которая ограничена линиями, достаточно значений первообразных на рисунке 1. Вычисление определенного интеграла заключается в получении первообразной и подстановке начального и конечного значений. Следует отметить, что константа при этом не берется. Существует способ, чтобы найти определенный интеграл. Формула Ньютона-Лейбница позволяет быстро и эффективно вычислить площадь фигуры. Для этого нужно подставить значения ее границ (a и b) в первообразные: F(x)|(a;b) = F(b) — F(a).
Криволинейные фигуры
Криволинейная фигура (трапеция) — класс плоских фигур, которые ограничены графиком неотрицательной и непрерывной функции, а также осью ОУ и прямыми (х = а, х = b). Она изображена на рисунке 2. Для нахождения ее площади следует использовать определенный интеграл.
Рисунок 2. Фигуры с криволинейными сторонами.
Интегрирование разбивает фигуру на прямоугольные части. Длина каждой из них равна ординате y = f(х) через промежутки, которые очень малы, по оси декартовой системы координат (есть еще и полярная) ОХ на отрезке [a;b]. Ширина является бесконечно малым значением. При интегрировании находятся площади прямоугольников и складываются. Для того чтобы не путаться в графиках, геометрическую фигуру следует заштриховать.
Криволинейная трапеция — геометрическая фигура с неровными сторонами, которые образовались в результате пересечения графика непрерывной функции с осями абсцисс и ординат.
Применение обыкновенных методов нахождения площади этой фигуры невозможно, поскольку она обладает одной или несколькими неровными сторонами (кривыми линиями).
Способы вычисления и рекомендации
Для расчетов площади криволинейной трапеции используется несколько методов. Их условно можно разделить на следующие: автоматизированные и ручные. Первый из них выполняется при помощи специализированного программного обеспечения (ПО). Примером является онлайн-калькулятор, который не только находит площадь заданной фигуры, но и изображает ее в декартовой системе координат.
Существует и другое ПО, которое является более «мощным». К нему можно отнести наиболее популярные среды: Maple и Matlab. Однако существует множество программ, написанных на языке программирования Python. Программы нужны также при освоении темы интегрирования. Если необходимо рассчитать множество интегралов и площадей криволинейных фигур, то без них не обойтись.
Новичку для автоматизированных вычислений рекомендуется применять различные онлайн-калькуляторы. Однако следует выделить неплохую программу, которая обладает довольно неплохими функциональными возможностями.
Она называется Integral calculator и представляет собой очень удобное приложение для Android-устройств. Кроме того, можно скачать подобное ПО для Linux, Mac и Windows.
Программа — это калькулятор, который используется для нахождения интегралов и производных, а также его можно применять для решения уравнений интегрального и дифференциального типов. Integral calculator обладает такими функциональными возможностями:
Однако специалисты не рекомендуют использовать приложения такого типа, поскольку нужно уметь решать подобные задачи самостоятельно. Любые математические операции развивают мышление, а злоупотребление ПО приводит к значительной деградации. Решать какие-либо задачи рекомендуется также людям, которые не имеют отношения к математической сфере.
Основной алгоритм
При нахождении площади криволинейной трапеции рекомендуется следовать определенному алгоритму. Он поможет избежать ошибок, поскольку задача разбивается на несколько простых подзадач, решение которых довольно просто контролировать. Алгоритм имеет следующий вид:
Первый пункт — внимательное чтение условия задачи. Этап считается очень важным, поскольку формирует дальнейший алгоритм. Необходимо выписать все известные данные, а затем подумать над дальнейшим решением задачи. Следует обратить особое внимание на график функции, который при возможности нужно упростить. Далее следует выписать линии, которые будут ограничивать фигуру.
Следующий пункт считается наиболее простым, поскольку нужно начертить обыкновенную систему координат. В условии должен быть указан ее тип. Если обозначена полярная система, то следует ее начертить. Во всех остальных случаях изображается декартовая система координат.
Третий пункт алгоритма — правильное построение графика функции. В этом случае нет необходимости составлять таблицу зависимости значения функции от аргумента. График должен быть схематичным. Например, если это парабола, то нужно ее изобразить. В этом случае необходимо ознакомиться с основными базовыми функциями и их графиками.
Следующим шагом является правильное изображение прямых. Если ее уравнение имеет следующий вид «x = 5» или что-то подобное, то она будет проходить параллельно оси ОУ. Например, при y = 10 прямая проходит параллельно оси ОХ. В других случаях нужно составить таблицу зависимостей значений уравнения прямой от переменной. Следует брать всего два значения аргумента, поскольку их достаточно для проведения прямой.
После всех операций образуется фигура, которая ограничена линиями. Ее необходимо заштриховать. После этого вычисляется неопределенный интеграл заданной функции. Необходимо воспользоваться табличными значениями первообразных на рисунке 2. Однако здесь есть небольшой нюанс: константу записывать нет необходимости. Она «уничтожается» при подстановке в формулу Ньютона-Лейбница.
В полученное значение следует подставить значения границ. Кроме того, необходимо обратить особое внимание на знак формулы. При отрицательном значении границы формула принимает следующий вид: F(x)|(-a;b) = F(b) — F(-a) = F(b) + F(a). Проверка правильности решения выполняется с помощью ПО.
Примеры решения
Для закрепления теоретического материала специалисты рекомендуют решить несколько задач. В качестве примера можно взять криволинейные трапеции, изображенные на рисунке 2.
Разновидность параболы
В первом примере функция вида y = -x^2 + 2x и ось ОХ образуют фигуру. Необходимо найти ее площадь. Из функции видно, что ветви параболы направлены вниз (отрицательный знак перед квадратом). Точки пересечения находятся следующим образом:
Ветви параболы проходят через координаты по ОХ: 0 и 2 соответственно. Координата «х» вершины точки параболы находится с помощью подстановки в формулу: x = -b/(2*a) = -2 / -2 = 1. В этом случае координата «у» вычисляется следующим образом: y = -(1^2) + 2 * 1 = -1 + 2 = 1. Точка с координатами (1;1) является вершиной параболы. Границы интегрирования — координаты по ОХ, через которые проходят ветви параболы.
После всех операций следует вычислить неопределенный интеграл функции, воспользовавшись таблицей на рисунке 1: ∫ (-х^2 + 2x) dx = — (x^3 / 3 + x^2) + C = x^2 — x^3 / 3 + C. После этого следует подставить начальное и конечное значения (константа убирается): S = x^2 — x^3 / 3 = (2^2 — 2^3 / 3) — (0^2 — 0^3 / 3) = 4 — 8/3 = 4 / 3 (кв. ед.). Последняя запись является единицей измерения площади. Она обозначается в условных единицах, так как в условии задачи размерность сторон фигуры не указана.
Гипербола, степенная и прямая
На следующем рисунке изображен график функции гиперболы (у = 1 / х). Прямые, которые ограничивают график, описываются следующими законами: у1 = -2 и у2 = -1. Для вычисления площади заданной фигуры следует взять интеграл: ∫(1/х) dx = ln (|x|) + С. Для окончательного решения необходимо подставить значения в натуральный логарифм: S = ln (2) — ln (1) = 0,6931 — 0 = 0,6931 (кв. ед.).
Фигура, которая ограничена прямыми y1 = -1 и y2 = 1, и представлена функцией вида y = 3^x. Площадь находится следующим образом: S = ∫ (3^x) dx = 3^x / (ln(|3|)) = [3^1 / (ln(3))] — [3^(-1) / (ln(3))] = (3 / 1,0986) — ((1/3) / 1,0986) = 2,7307 — 0,3034 = 2,4273 (кв. ед.).
Последняя фигура представлена графиком прямой y = 0,5х + 1, которую ограничивают прямые х1 = -1 и х2 = 2. Значение площади можно найти таким способом: S = ∫ (0,5х + 1) dx = (0,5 * х^2) / 2 + x = [((0,5 * 2^2) / 2) + 2] — [((0,5 * (-1)^2) / 2) + (-1)] = 3 — 0,75 = 2,25 (кв. ед.).
Для определения значения площади криволинейной фигуры (трапеции) необходимо использовать определенные интегралы. При решении нужно внимательно следить за знаками и первообразными из таблицы на рисунке 1.
1.8. Как вычислить площадь с помощью определённого интеграла?
Задачка это школьная, но, несмотря на то, почти 100% встретится в вашем курсе высшей математики. Поэтому со всей серьёзностью отнесёмся ко ВСЕМ примерам, и первое, что нужно сделать – это ознакомиться с Приложением Графики функций, чтобы освежить в памяти технику построения элементарных графиков. …Есть? Отлично! Типовая формулировка задания звучит так:
Пример 10
Вычислить площадь фигуры, ограниченной линиями .
И первый важнейший этап решения состоит как раз в построении чертежа. При этом я рекомендую следующий порядок: сначала лучше построить все прямые (если они есть) и только потом – параболы, гиперболы, графики других функций.
В нашей задаче: прямая определяет ось , прямые параллельны оси и парабола симметрична относительно оси , для неё находим несколько опорных точек:
Искомую фигуру желательно штриховать:
Второй этап состоит в том, чтобы правильно составить и правильно вычислить определённый интеграл. На отрезке график функции расположен над осью , поэтому искомая площадь:
Ответ:
После того, как задание выполнено, полезно взглянуть на чертёж
и прикинуть, реалистичный ли получился ответ.
И мы «на глазок» подсчитываем количество заштрихованных клеточек – ну, примерно 9 наберётся, похоже на правду. Совершенно понятно, что если бы у нас получилось, скажем, 20 квадратных единиц, то, очевидно, где-то допущена ошибка – в построенную фигуру 20 клеток явно не вмещается, от силы десяток. Если ответ получился отрицательным, то задание тоже решено некорректно.
Пример 11
Вычислить площадь фигуры, ограниченной линиями и осью
Быстренько разминаемся (обязательно!) и рассматриваем «зеркальную» ситуацию – когда криволинейная трапеция расположена под осью :
Пример 12
Вычислить площадь фигуры, ограниченной линиями , и координатными осями.
Решение: найдём несколько опорных точек для построения экспоненты:
и выполним чертёж, получая фигуру площадью около двух клеток:
Если криволинейная трапеция расположена не выше оси , то её площадь можно найти по формуле: .
В данном случае:
Ответ: – ну что же, очень и очень похоже на правду.
На практике чаще всего фигура расположена и в верхней и в нижней полуплоскости, а поэтому от простейших школьных задачек мы переходим к более содержательным примерам:
Пример 13
Найти площадь плоской фигуры, ограниченной линиями , .
Решение: сначала нужно выполнить чертеж, при этом нас особо интересуют точки пересечения параболы и прямой , поскольку здесь будут находиться пределы интегрирования. Найти их можно двумя способами. Первый способ – аналитический. Составим и решим уравнение:
таким образом:
Достоинство аналитического способа состоит в его точности, а недостаток – в длительности (и в этом примере нам ещё повезло). Поэтому во многих задачах бывает выгоднее построить линии поточечно, при этом пределы интегрирования выясняются как бы «сами собой».
С прямой всё понятно, а вот для построения параболы удобно найти её вершину, для этого возьмём производную и приравняем её к нулю:
– именно в этой точке и будет находиться вершина. И, в силу симметрии параболы, остальные опорные точки найдём по принципу «влево-вправо»:
Выполним чертеж:
А теперь рабочая формула: если на отрезке некоторая непрерывная функция больше либо равна непрерывной функции , то площадь фигуры, ограниченной графиками этих функций и отрезками прямых , можно найти по формуле:
Здесь уже не надо думать, где расположена фигура – над осью или под осью, а, грубо говоря, важно, какой из двух графиков ВЫШЕ.
В нашем примере очевидно, что на отрезке парабола располагается выше прямой, а поэтому из нужно вычесть
Завершение решения может выглядеть так:
На отрезке : , по соответствующей формуле:
Ответ:
Следует отметить, что простые формулы, рассмотренные в начале параграфа – это частные случаи формулы . Поскольку ось задаётся уравнением , то одна из функций будет нулевой, и в зависимости от того, выше или ниже лежит криволинейная трапеция, мы получим формулу либо
А сейчас пара типовых задач для самостоятельного решения
Пример 14
Найти площадь фигур, ограниченных линиями:
а) , .
б) , ,
Решение с чертежами и краткими комментариями в конце книги
В ходе решения рассматриваемой задачи иногда случается забавный казус. Чертеж выполнен правильно, интеграл решён правильно, но по невнимательности… найдена площадь не той фигуры, именно так несколько раз ошибался ваш покорный слуга. Вот реальный случай из жизни:
Пример 15
Вычислить площадь фигуры, ограниченной линиями
Решение: выполним бесхитростный чертёж,
хитрость которого состоит в том, что искомая площадь заштрихована зелёным цветом (внимательно смотрИте на условие – чем ограничена фигура!). Но на практике по невнимательности нередко возникает «глюк», что нужно найти площадь фигуры, которая заштрихована серым цветом! Особое коварство состоит в том, что прямую можно недочертить до оси , и тогда мы вовсе не увидим нужную фигуру.
Этот пример ещё и полезен тем, что в нём площадь фигуры считается с помощью двух определённых интегралов. Действительно:
1) на отрезке над осью расположен график прямой ;
2) на отрезке над осью расположен график гиперболы .
Совершенно понятно, что площади можно (и нужно) сложить:
Ответ:
И познавательный пример для самостоятельного решения:
Пример 16
Вычислить площадь фигуры, ограниченной линиями , , и координатными осями.
Итак, систематизируем важные моменты этой задачи:
На первом шаге ВНИМАТЕЛЬНО изучаем условие – КАКИЕ функции нам даны? Ошибки бывают даже здесь, в частности, арккотангенс зачастую принимают за арктангенс. Это, кстати, относится и к другим заданием, где встречается арккотангенс.
Далее следует ПРАВИЛЬНО выполнить чертёж. Сначала лучше построить прямые (если они есть), затем графики других функций (если они есть J). Последние во многих случаях выгоднее строить поточечно – найти несколько опорных точек и аккуратно соединить их линией.
Но здесь могут подстерегать следующие трудности. Во-первых, из чертежа не всегда понятны пределы интегрирования – так бывает, когда они дробные. На mathprofi.ru в соответствующей статье я рассмотрел пример с параболой и прямой , где из чертежа не понятна одна из точек их пересечения. В таких случаях следует использовать аналитический метод, составляем уравнение:
и находим его корни:
– нижний предел интегрирования, – верхний предел.
Во-вторых, не всегда понятен «внешний вид» линии, и функция (Пример 16) – яркий тому пример. Я и сам «с ходу» не представляю, как выглядит график этой функции. Здесь можно воспользоваться специализированными программами или онлайн сервисами (а-ля «построить график онлайн»), а в экстремальной ситуации найти побольше опорных точек (штук 10-15), чтобы поточнее провести «неизвестную» кривую.
Ну и, конечно, я призываю вас повышать свои знания и навыки в графиках, в частности, приведу прямую ссылку на особо полезную статью:
http://mathprofi.ru/kak_postroit_grafik_funkcii_s_pomoshyu_preobrazovanii.html
После того, как чертёж построен, анализируем полученную фигуру – ещё раз окидываем взглядом предложенные функции и перепроверяем, ТА ЛИ это фигура. Затем анализируем её форму и расположение, бывает, что площадь достаточно сложнА и тогда её следует разделить на две, а то и на три части.
Составляем определённый интеграл или несколько интегралов по формуле , все основные вариации мы разобрали выше.
Решаем определённый интеграл (ы). При этом он может оказаться достаточно сложным, и тогда применяем поэтапный алгоритм: 1) находим первообразную и проверяем её дифференцированием, 2) используем формулу Ньютона-Лейбница.
Результат полезно проверить с помощью программного обеспечения / онлайн сервисов или просто «прикинуть» по чертежу по клеточкам. Но и то, и другое не всегда осуществимо, поэтому крайне внимательно относимся к каждому этапу решения!
Полную и свежую версию данного курса в pdf-формате ,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
http://rus-shkola.ru/matematika/metody-vychisleniya-ploshhadi-figury-ogranichennoj-liniyami/
http://mathprofi.com/knigi_i_kursy/integraly/1_8_kak_vychislit_ploshad_figury_s_pomoshyu_opredelennogo_integrala.html
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Вычислить площадь, ограниченную окружностью и параболой
|
|||
|
Окружность: [math]x^2+y^2=16[/math], парабола: [math]x^2=12 cdot (y-1)[/math]. Рисунок . Как я понимаю, удобнее перейти к полярным координатам: Но интеграл [math]intlimits_{- frac{pi}{6}}^{frac{pi}{6}} d varphi intlimits_{frac{6}{1-sin(varphi)}}^{4} r dr[/math] равен отрицательному значению. Подскажите пожалуйста, что я делаю не так. p.s. Про симметрию знаю.
|
||
| Вернуться к началу |
|
||
 |
Добавлено: 01 фев 2013, 21:14 
|
Avgust |
Заголовок сообщения: Re: Вычислить площадь, ограниченную окружностью и параболой
|
|
Решал в декартовых координатах [math]S=2int limits_{0}^{2sqrt{3}}left ( sqrt{16-x^2}-frac{x^2}{12}-1 right ) dx =[/math] [math]= x sqrt{16-x^2}+16 arcsin left ( frac x4 right )-frac{x^3}{18}-2x bigg |_0^{2sqrt{3}}=[/math] [math]=frac{16pi}{3}-frac{4}{sqrt{3}}approx 14.446[/math]
|
|
| Вернуться к началу |
|
|
|
| За это сообщение пользователю Avgust «Спасибо» сказали: Wersel |
|
|
|
Avgust |
Заголовок сообщения: Re: Вычислить площадь, ограниченную окружностью и параболой
|
|
Нууу! Я такие вещи, как пересечения, легко делаю ручками. [math]frac{x^4}{144}+frac{7x^2}{6}-15=0[/math] ??? Неужели Вы такого интеграла не знаете: [math]int sqrt{a^2-x^2}, dx=frac x2 sqrt{a^2-x^2}+frac{a^2}{2}arcsin left ( frac{x}{|a|} right )+ C[/math] Его должен знать каждый, кто работает с окружностями. Последний раз редактировалось Avgust 01 фев 2013, 22:26, всего редактировалось 1 раз. |
|
| Вернуться к началу |
|
|
|
Wersel |
Заголовок сообщения: Re: Вычислить площадь, ограниченную окружностью и параболой
|
|
Avgust писал(а): Неужели Вы такого интеграла не знаете: [math]int sqrt{a^2-x^2}, dx=frac x2 sqrt{a^2-x^2}+frac{a^2}{2}arcsin left ( frac{x}{|a|} right )+ C[/math] Его должен знать каждый, кто работает с окружностями. Я — знаю, но он — не табличный.
|
|
| Вернуться к началу |
|
|
Пусть функция
имеет разрывII
рода на [a,b]
либо в точках а и b,
либо в точке
,
тогда несобственные интегралы от
разрывной функции определяются следующим
образом:
1)
точка разрыва, то
;
2)
точка разрыва, то
,
3)
,
с
точка разрыва, то
Если указанные
пределы существуют и конечны, то
несобственные интегралы называются
сходящимися, в противном случае
расходящимися.
Признак сравнения.
Пусть функции f(x)
и g(x)
в промежутках [a,b)
непрерывны, а в точке
имеют разрывII
рода; кроме того
.
Если
сходится, то сходится
.
Если
расходится, то расходится
.
Пример 41.
Исследовать на сходимость несобственный
интеграл
.
Решение.
Функция
в точке
имеет разрывII
рода, поэтому
.
Интеграл расходящийся.
Пример 42.
Исследовать на сходимость несобственный
интеграл от неограниченной функции
Решение.
При
знаменатель функции обращается в 0, а
числитель равен 1, следовательно,
точка разрыва II
рода. Во всех остальных точках промежутка
(0;1] подынтегральная функция непрерывна.
Заметим также, что
,
Используя определение
несобственного интеграла от неограниченной
функции, а также формулу Ньютона-Лейбница
получим
Интеграл сходящийся.
4. Приложения определенного интеграла
4.1. Вычисление площади плоской фигуры в декартовых координатах
Если задана
непрерывная функция
на [a,b],
,
то определенный интеграл с геометрической
точки зрения представляет собой площадь
так называемой, криволинейной трапеции
(рис.4.1).
(4.1)
Пусть криволинейная
трапеция с основанием [a,b]
ограничена снизу кривой
(рис.4.2), то из соображений симметрии
видим, что
(4.2)
В некоторых случаях,
чтобы вычислить площадь искомой фигуры,
необходимо разбить ее на сумму или
разность двух или более криволинейных
трапеций и применить формулы (4.1) или
(4.2) (рис.4.3. и 4.4)
(4.3)
Пример 43.
Вычислить площадь фигуры, ограниченной
линиями
и
.
Решение.
парабола. Найдем ее вершину и точки
пересечения с осями координат.
;
или
,
Если
,
то
вершина параболы.
или
или
.
прямая линия.
Найдем абсциссы
точек пересечения прямой и параболы:
или
.
Для вычисления
площади заштрихованной области
воспользуемся формулой (4.4)
П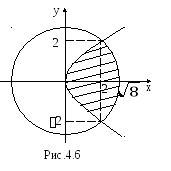
ример
44. Вычислить
площадь двух частей, на которые круг
разделен параболой
.
Решение.
Сделаем чертеж (рис.4.6)
окружность с
центром
в начале координат
и радиусом
.
парабола, имеющая
вершину
в т.О(0,0)
Найдем точки
пересечения параболы
и окружности:
не удовлетворяет
условию
.
Если
,
то
или
,
Найдем площадь
заштрихованной области по формуле
(4.4), в которой изменены переменные
интегрирования:
;
.
.
Найдем площадь
второй (незаштрихованной) части, на
которую круг разделен параболой
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
17.12.2018552.96 Кб35KA.doc
- #
Содержание:
- Примеры с решением
Пусть требуется найти площадь фигуры, ограниченной графиками функций 
и 
. Площадь требуемой фигуры 
на рисунке можно найти, вычитая из площади 
площадь 
Каждую площадь можно вычислить как определенный интеграл на заданном промежутке.
Эти суждения можно обобщить следующим образом. 
Так как функции 
и 
непрерывны на отрезке 
и на этом отрезке выполняется условие 
(т.е.график функции 
) расположен выше графика функции то площадь ограниченная графиками функций 
и прямыми 
можно выразить следующим выражением: 
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Графики функций не имеют общих точек.
Примеры с решением
Пример 1.
Найдите площадь, ограниченную графиками функций 
и 
и прямыми 
Решение:
=
Графики функций пересекаются в двух точках.
Пример 2.
Найдите площадь, ограниченную графиками функций 
Решение:
Найдем абсциссы точек пересечения графиков функций.
Полученные значения
являются границами определенного интеграла.
Возможно вам будут полезны данные страницы:
Пример 3.
Найдите площадь, заключенную между графиками функций 
и 
Решение:
Найдем абсциссы точек пересечени графиков.
Значит, графики пересекаются в точках с абсциссами 
По графикам функций также видно, что площадь, которую мы должны найти, состоит из площади, ограниченной графиками на промежутке 
и на промежутке 
На промежутке 
выполняется условие 
на промежутке 
выполняется условие 
(разность функций учитываются при записи интеграла).
! Вычислите требуемую площадь при помощи интеграла
Какой результат вы получили?
Пример 4.
Члены школьного клуба юных конструкторов работают над созданием нового двигателя для автомобиля, который будет меньше засорять окружающую среду. Для нового мотора изменение количества частиц (млрд), загрязняющих атмосферу, в 
год можно выразить следующим образом: 
Количество загрязняющих частиц, выбрасывамых старым мотором имеет вид: 
a) В какой год они будут выбрасывать в атмосферу одинаковое количество частиц?
b) Какова разница между количеством вредных частиц, выброшенных в атмосферу, за этот период
Решение:
а) при 
удовлетворяющего условию 
количество вредных частиц будет одинаково.
Значение 
не соответствует смыслу задачи. На 3-ий год новый мотор будет давать такое же количество вредных частиц, как и старый. b) Разность количества вредных частиц равна разности площадей на промежутке [0;3]. 
(млрд. частиц)
Пример 5.
Вычислить площадь фигуры, ограниченной параболой 
и окружностью 
Решение:
Сначала схематически изобразим эту площадь. Из рисунка видим
что заданные кривые ограничивают две различающиеся плоские фигуры (меньшую и большую). Каждая из этих фигур, в свою очередь, состоит из двух симметричных относительно оси 
частей.
Поэтому достаточно вычислить площадь верхней части каждой фигуры и затем умножить ее на два.
Найдем сначала площадь меньшей фигуры. Преобразуем уравнение окружности и определим координаты ее центра и величину радиуса.
Следовательно, центр окружности находится в точке 
а ее радиус 
Найдем точки 
и 
пересечения обеих линий, решая систему двух
уравнений 
Найдем уравнение границы 
(части окружности) 
Из условия на ординаты точек границы 
имеем 
по этой же причине уравнение нижней части границы 
на отрезке 
По формуле (1) находим
но 
— это площадь четверти окружности. Площадь всей окружности равна 
Второй интеграл легко вычисляется 
Теперь найдем искомую площадь
Теперь, чтобы найти площадь большей фигуры, необходимо из площади круга вычесть площадь меньшей фигуры: 
Проверим значение первого интеграла
Обозначим 
тогда 
при 
при 
(четвертая четверть). Поэтому
Пример 6.
Вычислить площадь фигуры, ограниченной линиями 
и 
Решение:
Второе уравнение запишем так 
, отсюда следует, что 
это означает, что вся фигура (парабола) 
расположена левее точки 
она симметрична относительно оси 
так как при замене 
на 
уравнение не изменяется. Ветви параболы направлены влево; ее вершина находится в точке 
Определим точки ее пересечения с осью 
Ветви второй параболы направлены также влево, а ее вершина совпадает с началом координат.
Определим точки пересечения этих кривых из решения системы
Одна точка пересечения 
вторая — 
Изобразим эту фигуру на чертеже. Здесь проще вычислить площадь по формуле (2) т. е.
Лекции:
- Подобие фигур
- Элементарные функции
- Пересекающиеся плоскости
- Как найти производную: примеры решения
- Дифференциальные уравнения примеры решения
- Производная сложной функции
- Многоугольники
- Арифметические операции над пределами
- Метод Гаусса: пример решения
- Производные показательной и логарифмической функций
Площадь S криволинейного сектора, ограниченного непрерывной кривой r=r(f) и двумя лучами f=f1 и f=f2, где f1<f2 равняется половине определенного интегралу от квадрата радиуса кривой, проинтегрированного в пределах изменения угла
Задачи взяты из программы практикума для студентов мех-мата Львовского национального университета имени Ивана Франко. Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича).
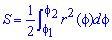
Для запоминания основных моментов схема интегрирования и нахождения площадей из примера в пример будет повторяться. Сами ррешеня по возможности будут проиллюстрированы графиками исследуемых кривых.
Найти площади фигур, ограниченных кривыми, заданными в полярных координатах
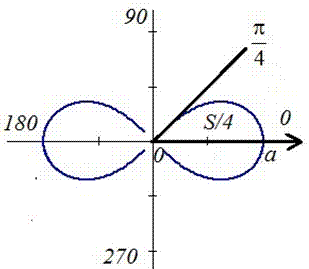
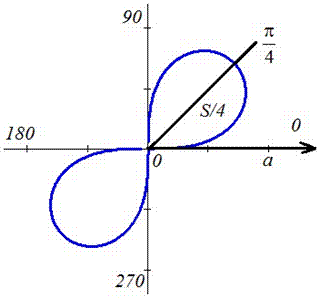
Пример 2.106 (2418) Вычислить площадь фигуры, ограниченной кривыми r2=a2*cos(2f) (лемниската Бернулли).
Вычисление: Лемниската Бернулли — геометрическое место точек, произведение расстояний от которых до двух фиксированных точек (фокусов) остается постоянным и равняется квадрату половины расстояния между фокусами.
Запишем подинтегральную функцию: r2=a2*cos(2f) (известна за условием).
Найдем пределы интегрирования:
задана кривая замкнутая, симметричная относительно прямых r*cos(f)=0 и r*sin(f)=0.
Наведем график лемнискаты Бернулли
Поскольку заданная функция осями координат делится на четыре равных части и достигает своих критических значений при f1=0 (r=a) и f2=p/4 (r=0), то площадь фигуры вычислим для одной части лемнискаты, а результат умножим на 4.
Найдем площадь фигуры интегрированиям по углу
Площадь измеряется в единицах квадратных, однако в этом и следующих примерах размерности наводить не будем, хотя о них помним.
Пример 2.107 (2419) Найти площадь фигуры, ограниченной кривыми r=a* (1+cos(f)) — кардиоида.
Вычисление: Кардиоида — плоская линия, которая описывается фиксированной точкой круга, который катится по неподвижному кругу с таким же радиусом a.
Записываем подинтегральную функцию: r2=a2*(1+cos(f))2.
Находим пределы интегрирования: кривая замкнутая, симметричная относительно прямой r*sin(f) =0.
Поскольку заданная функция осями координат делится на две равных части и достигает своих критических значений при f1=0 (r=2a) и f2=p (r=0), то площадь фигуры вычислим для половины кардиоиды, а результат умножим на 2.
График кардиоиды имеет вид
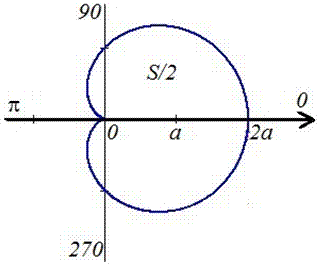
Вычислим площадь фигуры, которая ограничена заданной кривой, интегрированием:
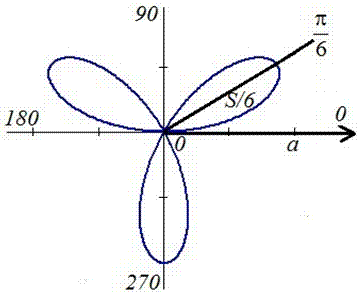
Пример 2.108 (2420) Найти площадь фигуры, ограниченной кривой r=a*sin(f) -трилисник.
Вычисление: Подносим функцию к квадрату, чтобы получить подинтегральную функцию:
r2=a2*sin2(f).
График трилистника в полярной системе координат
Установим пределы интегрирования:
Поскольку заданный график функции делится на шесть равных частей (полупелюсток) и достигает своих критических значений при f1=0 (r=0) и f2=p/6 (r=a/2) то площадь фигуры вычислим для одной его части, а результат умножим на 6.
Находим площадь фигуры интегрированием по углу
Получили простую для вычислений формулу площади трилистника S=Pi*a2/4.
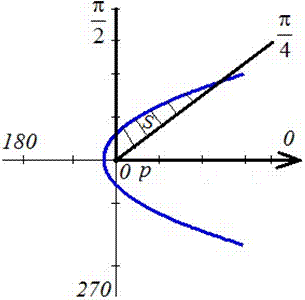
Пример 2.109 ( 2421) Вычислить площадь фигуры, ограниченной кривой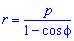 
(парабола), f1=p/4, f2=p/2.
Вычисление: Подносим к квадрату уравнения кривой в полярной системе коринат (СК).
Пределы интегрирования известны f1=p/4, f2=p/2 за условием.
График фигуры, площадь которой нужно найти имеет вид
Интегрированием вычисляем площадь фигуры, которая ограничена параболой:
Для вычисления интеграла следует выполнить замену переменных, не забывая при этом , что изменяются пределы интегрирования.
Пример 2.110 ( 2422) Найти площадь фигуры, ограниченной кривой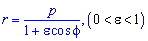 
(эллипс)
Вычисление: Запишем подинтегральную функцию:
Пределы интегрирования: f1=0, f2=2p (начало и конец кривой эллипса).
График эллипса имеет вид
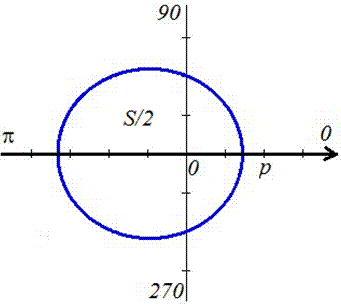
Находим площадь елипса, воспользовавшись следующей формулой интегрирования
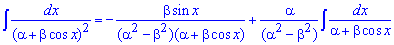
При выведении этой формулы пользовались методом интегрирования частями!
Напоследок превращаем конечную формула с помощью известных формул.
Как видим, ответы задач 2.110 и 2.87 совпадают, то есть площадь эллипса S=Pi*a*b вычислена правильно.
Пример 2.111 (2422.1) Найти площадь фигуры, ограниченной кривой заданной в полярных координатах r=3+2*cos(f).
Вычисление: Сначала находим подинтегральную функцию: r2=(3+2*cos(f))2.
Дальше пределы интегрирования: задана кривая замкнутая, симметричная относительно прямой r*sin(f)=0.
Ее график приведен на рисунку ниже
Поскольку задана кривая осями координат делится на две равных части и достигает своих критических значений при углах f1=0 (r=5) и f2=p (r=1), то вычислим половину площади фигуры, а результат умножим на 2.
Находим площадь фигуры через определенный интеграл
Интеграл в данном случае не тяжелый и, возведя в квадрат подинтегральную функцию и понизив квадрат косинуса, в результате вычислений получим, что площадь равна S=11*Pi.
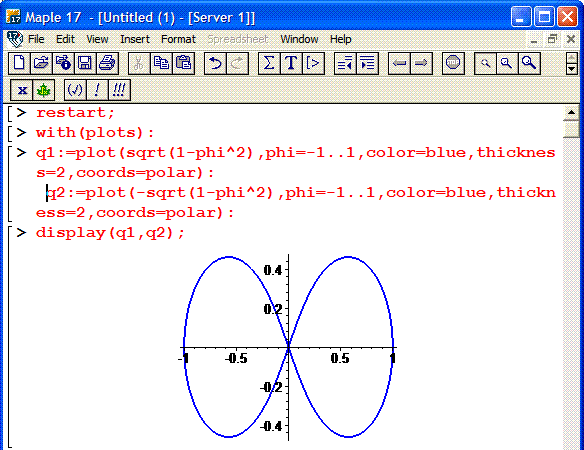
Пример 2.112 (2424.1) Найти площадь фигуры, ограниченной кривой заданной в полярных координатах r2+f2=1.
Вычисление: Выражаемый подинтегральную функцию: r2=1-f2 .
Найдем пределы интегрирования.
, поэтому 
, откуда 
.
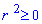
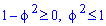
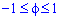
Построим график кривой в математическом пакете Maple17.
Кривая состоит из двух веток корневой функции, поэтому для корректного ее отображения используем следующий код:
> restart;
> with (plots) :
> q1:=plot(sqrt(1-phi^2),phi=-1.1, color=blue, thickness=2, coords=polar):
q2:=plot(-sqrt(1-phi^2),phi=-1.1, color=blue, thickness=2, coords=polar):
> display (q1, q2);
Фрагмент программы Maple приведен ниже
Находим площадь фигуры, которая ограничена кривой:
Интеграл в этом задании простей всех, что рассматривались.
Пример 2.113 ( 2422.2) Вычислить площадь фигуры, ограниченной кривыми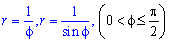 
.
Вычисление: Выписываем подинтегральные функции:
Поскольку на промежутке интегрирования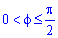 
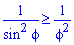
между кривыми выполняется неравенство
, то для нахождения площади имеем r22-r12.
Найдем пределы интегрирования: f1=0 — особенная точка (функция направляется к безграничности) f1=p/2 (известны за условием).
Находим площадь фигуры через предел от интеграла:
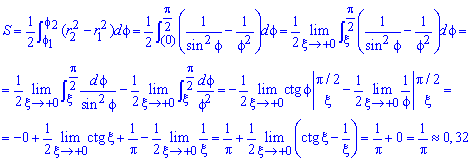
Данный пример хорошо разберите, чтобы не иметь трудностей на экзамене или модуле с подобными.
Пример 2.114 ( 2424) Вычислить площадь фигуры, ограниченной кривой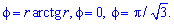 
Вычисление: Запишем подинтегральную функцию: r2.
Запишем пределы интегрирования:
(известны за условием).
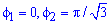
График функций имеет вид
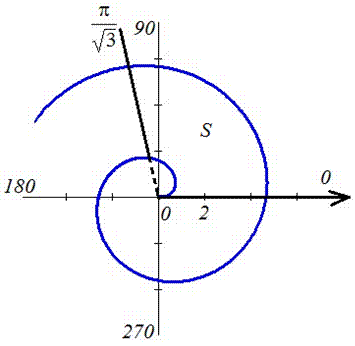
Вычислим площадь фигуры, что приведена на графике.
Для этого сначала находим дифференциал угла f и переходим к интегрированию по радиусу.
Для нахождения интеграла применяем интегрирование частями
Интеграл достаточно трудно находится, поэтому все что содержит формула внимательно проанализируйте.
Пример 2.116 (2424.4) Найти площадь фигуры, ограниченной полярными кривыми f=r-sin(r), f=p.
Вычисление: Подинтегральную функция следующая: r2.
Пределы интегрирования: f1=0, (r=0) начало; f1=p (известно за условием).
График функции имеет вид
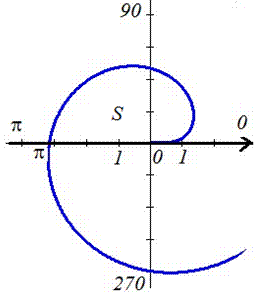
Находим площадь фигуры, применяя дважды интегрирование частями
Интеграл не слишком сложен, все переходы просьба проанализировать самостоятельно.
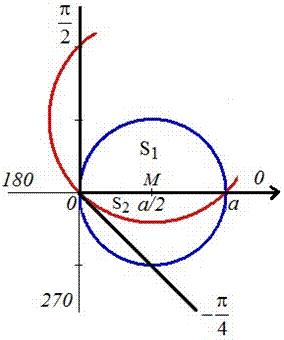
Пример 2423 Вычислить площадь фигуры, ограниченной полярными кривыми r=a*cos(f), r=a(cos(f)+sin(f)), M (a/2;0)єS.
Вычисление: Для представления фигуры, площадь которой нужно найти предварительно выполняем построение графика заданных функций
Поскольку точка M (a/2;0)єS делит искомую площадь на две части, то имеем два интеграла
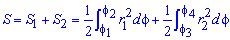
Записываем уравнение подинтегральных функций:
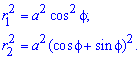
Определяем пределы интегрирования:
, где 
и 
где 
(точки пересечения линий).
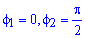
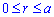
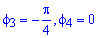
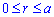
Вычисляем площадь изображенной фигуры интегрированием
Здесь воспользовались известные тригонометрические формулы для понижения степени косинусов и синусов под интегралом. Все остальное сводятся к применению простых формул интегрирования, и нахождения их значений.
Пример 2424.2 Найти площадь фигуры, ограниченной полярными кривыми f=sin(p*r), r пренадлежит [0;1].
Вычисление: Запишем подинтегральную функцию: r2.
Запишем пределы интегрирования: При росте r от 0 к 1/2 угол f растет от 0 к 1, при росте r от 1/2 к 1 угол f спадает от 1 к 0, поэтому величина интеграла в пределах r пренадлежит [0;1] имеет знак «минус».
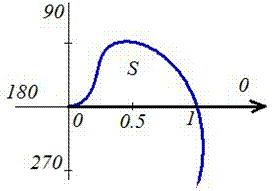
Находим площадь фигуры, предварительно перейдя к новой переменной под интегралом:
Перед интегралом (после замены переменных) поставили знак «минус», поскольку интеграл является отрицательным на этом промежутке, а площадь должна быть положительной.
Перейти к полярным координатам и найти площади фигур, ограниченных кривыми
Пример 2426 Перейти к полярным координатам и найти площадь фигуры x3+y3=3a*x*y (лист Декарта)
Вычисление: Перейдем от прямоугольной системы координат к полярной системе координат за формулами перехода:
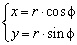
При подстановке в уравнение получим
Поднесем к квадрату, чтобы получить подинтегральную функцию:
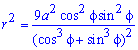
Выпишем пределы интегрирования:
, потому что 
при 
и при 
.
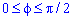
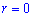
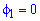
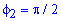
График функции имеет вид
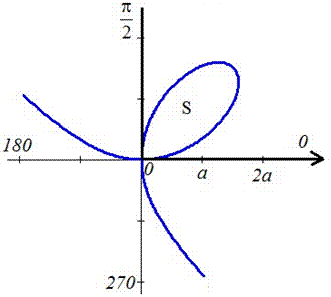
Найдем площадь фигуры интегрированиям:
Для получения конечной формулы площади дважды применяли замену переменных под интегралом.
Внимательно разберите, как при этом изменяются пределы и эффективность методики.
Пример 2427 Перейти к полярным координатам и найти площадь фигуры x4+y4=3a2(x2+y2)
Вычисление: Переходим от прямоугольной к полярной системе координат:
Выражаемый подинтегральную функцию делением:
Запишем пределы интегрирования:
(функция парная).
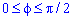
Ее график изображен на рисунку
Оси прямоугольной системы координат являются осями симметрии для фигуры, которая ограничена заданной линией, поэтому площадь найдем для симметричной части и результат умножим на 4.
Находим площадь фигуры через интеграл:
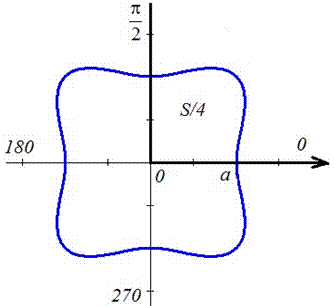
Пример 2428 Перейти к полярным координатам и найти площадь фигуры (x2+y2)2=2a2*x*y (лемниската).
Вычисление: Выполняем переход от прямоугольной к полярной системе координат:
— подинтегральная функция.
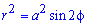
График исследуемой кривой следующий
Запишем пределы интегрирования: учитывая симметрию точек лемнискаты относительно прямой r*sin(f) =r*cos (f) и относительно начала координат, то площадь фигуры будем искать в пределах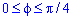 
и результат умножим на 4 (смотри пример 2.106).
Находим площадь фигуры интегрированием:
Вычислений в этом задании минимум.
В следующих публикациях Вы найдете больше примеров на применение определенного интеграла при вычислении длины дуги, объемов фигур вращения и площадей поверхностей.