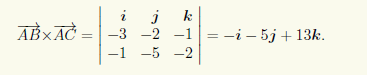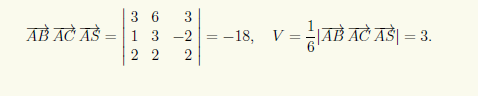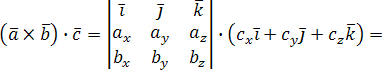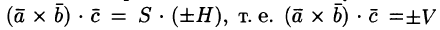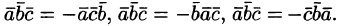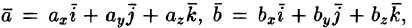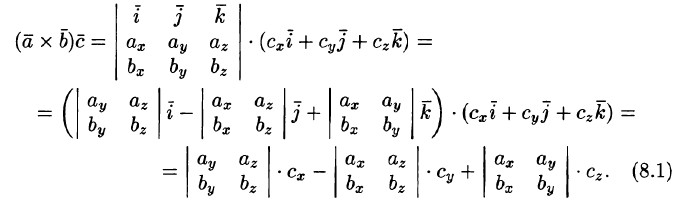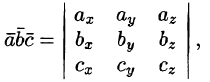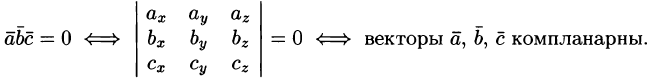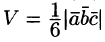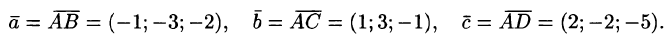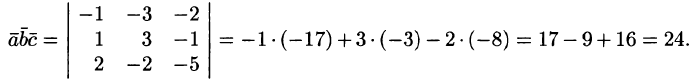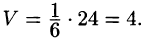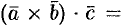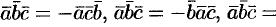Объем параллелепипеда, построенного на векторах онлайн
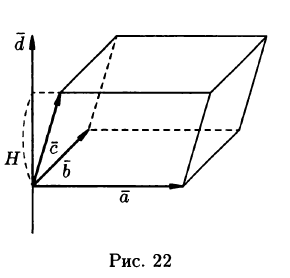
Объём параллелепипеда равен смешанному произведению векторов на которых он построен:
Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела — всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:
Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.
Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.
Смешанное, векторное и скалярное произведение векторов
Задача:
Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).
Найти:
Решение:
- а) Объем параллелепипеда будем искать через смешанное произведение векторов (AB AD AA1). Мы знаем, что модуль смешанного произведения векторов равен объему параллелепипеда, построенному на этих векторах.
| (AB AD AA1) | = |
|
= | 20 — 18 + 0 — 0 — 30 + 16 | = | -12 | . |
|---|
Мы нашли смешанное произведение, ещё надо его взять по модулю и найдём объем параллелепипеда:
VABCDA1B1C1D1=12.
б) Площадь, как мы уже знаем, можно искать через векторное произведение векторов. Грань ABCD построена на векторах AB и AD, найдём их векторное произведение. SABCD= |[AB AD]|.
| [AB AD] | = |
|
= | 6i — 8j — 2k | , |
|---|
Теперь найдём модуль этого вектора:
| SABCD= |[AB AD]|=√ | (36+64+4) | =2√(26). |
|---|
| [AD AA1] | = |
|
= | 9i — 16j — k | , |
|---|
SADD1A1= |[AD AA1]|=√(81+256+1)=13√2.
| h | = |
|
= |
|
= |
|
= |
|
. |
|---|
| cos(λ1) | = |
|
. |
|---|
Координаты вектора AB мы имеем, от вектор B1D надо найти. Для этого используем следующую формулу:
B1D = B1A1 + A1A + AD = — AB — AA1 + AD1 = — (4, 3, 0) — (-3, -2, 5) + (2, 1, 2); (Не забывайте, что всё это векторы, надо сложить их соответствующие координаты. )
Сделав вычисления по этой формуле, мы найдём, что вектор B1D имеет координаты (1, 0, -3). Теперь надо найти длину векторов AB и B1D:
|AB|=√(16+9+0)=5, |B1D|=√(1+0+9)=√(10).
Найдём скалярное произведение векторов AB и B1D, (AB B1D)=4*1 + 3*0 + 0*(-3)=4.
Теперь, имея все данные мы можем подставить их в нашу формулу:
| cos(λ1) | = |
|
= |
|
. |
|---|
д) Что бы найти cos(λ2), мы используем то, что угол между двумя плоскостями равен углу между перпендикулярами до этих плоскостей. А как мы знаем, векторное произведение — это и есть перпендикуляр до плоскости перемножаемых векторов. Поэтому в роле перпендикуляра к плоскости ADD1A1 мы можем взять вектор [AD AA1], который мы нашли в пункте б), и знаем, что его координаты (9, -16, -1), точно также и для плоскости ABCD — вектор [AB AD] с координатами (6, -8, -2).
Теперь нам остаётся, как в предыдущем варианте найти только косинус угла между двумя векторами, координаты которых нам известны.
| cos(λ2) | = |
|
= |
|
. |
|---|
Вот таким не хитрым способом мы и нашли косинус угла между гранями ABCD и ADD1A1.
Нахождение площади прямоугольного параллелепипеда: формула и пример
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:
Формула получена следующим образом:
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a и b;
- четыре боковые грани: со стороной a/b и высотой c.
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см 2 .
http://matemonline.com/primeru/zada4a-na-vektor/
Нахождение площади прямоугольного параллелепипеда: формула и пример
Вычисление площадей многоугольников и объемов многогранников, заданных координатами своих вершин в прямоугольной системе координат, основывается на использовании скалярного, векторного и смешанного произведений векторов.
Если параллелограмм задан в пространстве координатами своих вершин, то для вычисления его площади нужно найти координаты двух векторов, соответствующих смежным сторонам параллелограмма, а затем модуль их векторного произведения. Аналогично вычисляется площадь треугольника, равная половине модуля векторного произведения векторов, на которых он построен как на смежных сторонах.
Пример 4.2. Пусть три вершины треугольника заданы своими координатами: A(4;4;4), B(1; 2; 3), C(3; —1;2).
Для определения площади ΔABC с помощью (4.10) найдем координаты векторов AB и AC: AB = {1 — 4; 2 — 4; 3 — 4} = { — 3; —2; —1}, —1 = {3 — 4; —1 — 4; 2 — 4} = { — 1; —5; —2}.
Затем по (3.2) вычислим их векторное произведение:
Модуль этого векторного произведения равен |AB×AC| = √((—1)2 + (—5)2 + 132) = √195, и следовательно, S ΔABC = |AB×AC|/2 = √195/2 #
Для вычисления объема параллелепипеда, заданного координатами своих вершин, нужно найти координаты трех векторов, соответствующих смежным ребрам, а затем вычислить модуль смешанного произведения этих векторов. Через смешанное произведение вычисляется и объем произвольной треугольной пирамиды SABC (см. пример 3.2), поскольку он равен 1/6 объема параллелепипеда, построенного на ребрах AB, AC и AS. Таким образом, объем этой пирамиды равен VSABC = |ABACAS|/6.
Пример 4.3. Найдем объем V пирамиды SABC, заданной координатами своих вершин: A(2; —1;1), B(5; 5; 4), C(3; 2; —1), S(4;1;3).
Используя (4.10), вычисляем координаты векторов, направленных по ребрам пирамиды: AB = {5 — 2; 5 — (—1);4 — 1} = {3; 6; 3}, AC = {3 — 2; 2 — (—1); —1 — 1} = {1;3; —2},= AS {4 — 2;1 — (—1); 3 — 1} = {2;2;2}, и определяем объем с помощью смешанного произведения найденных векторов:
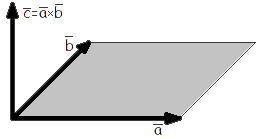
Векторным
произведениемвектора a на вектор b
называется вектор c, длина которого
численно равна площади параллелограмма
построенного на векторах a и b,
перпендикулярный к плоскости этих
векторов и направленный так, чтоб
наименьшее вращение от a к b вокруг
вектора c осуществлялось против часовой
стрелки, если смотреть с конца вектора
c (рис. 1).
|
|
|
рис. 1 |
Формулы
вычисления векторного произведения
векторов
Векторное
произведениедвух векторов a = {ax;
ay; az} и b = {bx; by;
bz} в декартовой системе координат
— это вектор, значение которого можно
вычислить, используя следующие формулы:
|
a × b = |
i |
j |
k |
= i(aybz |
|
ax |
ay |
az |
||
|
bx |
by |
bz |
a × b = {aybz— azby; azbx— axbz;
axby— aybx}
Свойства
векторного произведения векторов
-
Геометрический смысл векторного
произведения.
Модуль векторного произведения двух
векторов a и b равен площади параллелограмма
построенного на этих векторах:
Sпарал= a × b]
-
Геометрический смысл векторного
произведения.
Площадь треугольника построенного на
векторах a и b равна половине модуля
векторного произведения этих векторов:
|
SΔ = |
1 |
|a × b| |
|
2 |
-
Векторное произведения двух не нулевых
векторов a и b равно нулю тогда и только
тогда, когда вектора
коллинеарны. -
Вектор c, равный векторному произведению
не нулевых векторов a и b, перпендикулярен
этим векторам. -
a × b = -b × a
-
(k a) × b = a × (k b) = k (a × b)
-
(a + b) × c = a × c + b × c
14. Смешанное произведение векторов, его свойства. Условие компланарности вектора. Объем параллелепипеда. Объём пирамиды.
Смешанным
произведением
некомпланарныхвекторов
,взятых в данном порядке, называетсяобъём параллелепипеда, построенного
на данных векторах, снабжённый знаком
«+», если базисправый,
и знаком «–», если базислевый.
1.
Смешанное
произведение не меняется при циклической
перестановке его сомножителей (не
меняется ни объем параллелепипеда, ни
ориентация его ребер):
.
2.
Смешанное
произведение не меняетсязнаков
векторного и скалярного умножения:,
поэтому смешанное произведение записывают.
3.
Смешанное
произведение меняет свой знак при
перемене любых двух вектор-сомножителей:
,
.
4.
Смешанное
произведение ненулевых векторов
,
и
равно
нулю тогда и только тогда, когда они
компланарны:,
,
–
компланарны.
Доказательство.
Предположим, что векторы
,
и
–
не компланарны. Тогда можно построить
параллелепипед имеющий объем,
т.е.,
но это противоречит условию, согласно
которого,.
Следовательно, векторы,
и
–
компланарны.
Обратно,
пусть
,
и
–
компланарны. Тогда вектори
перпендикулярен плоскости, в которой
находятся векторы,
и
,
значит, он перпендикулярен любому
вектору, лежащему в этой плоскости,
напримерЭто
значит, что
.
Смешанное
произведение векторов, заданных своими
проекциями в декартовой системе
координат.
Пусть
векторы заданы своими разложениями по
ортам в декартовой системе координат:
,
и
.
Найдем
их смешанное произведение, используя
выражения в координатах для векторного
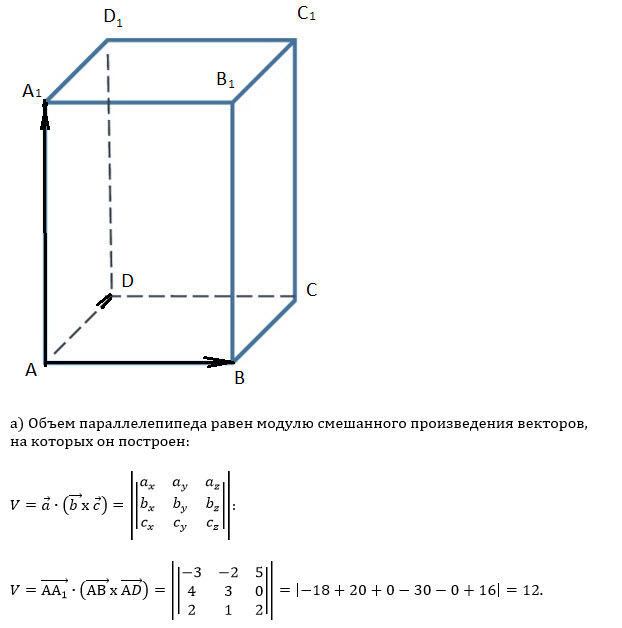
и скалярного произведений:
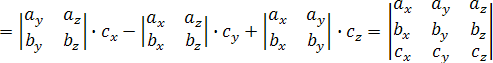
Итак,
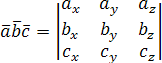
Приложения
смешанного произведения:
1.
Определение
взаимной ориентации векторов в
пространстве.
Если
,
и
–
правая тройка, еслилевая.
2.
Установление
компланарности векторов:
(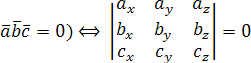
(,
,
–
компланарны).
3.
Определение
объема параллелепипеда и треугольной
пирамиды (тетраэдра):
,
.
Пример.
Компланарны ли векторы
,
и
,
если
.
Решение.
Вычислим смешанное произведение
векторов:
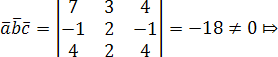
,
и
не
компланарны.
Пример.
Доказать, что векторы
,
и
компланарны.
Решение.
Рассмотрим матрицу, составленную из
координат векторов
,
и
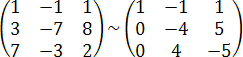
т. к. определитель матрицы равен нулю,
то векторы линейно зависимы, следовательно
они компланарны.
Пример.
Вычислить объем тетраэдра с вершинами
в точках
и
его высоту, опущенную из вершинына
грань,
если
Решение.
Найдем координаты векторов:
,
,
.
Вычислим
объем:
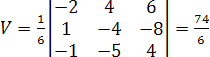
Поскольку
объем тетраэдра
,
то высота.
Вычислим
площадь основания тетраэдра
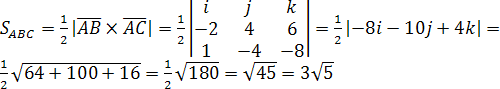
Итак,
высота
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение смешанного произведения, его геометрический смысл:
Рассмотрим произведение векторов 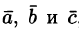
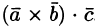
Выясним геометрический смысл выражения 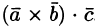
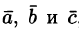
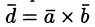
Имеем: 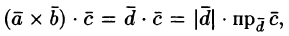
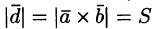
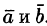
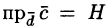
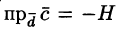
где V — объем параллелепипеда, образованного векторами 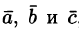
Таким образом, смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.
Свойства смешанного произведения
1.Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е.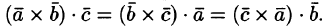
2. Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения, т. е. 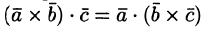
Действительно, 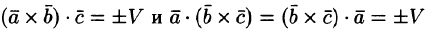
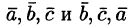
Следовательно, 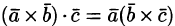
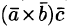
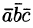
3. Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей, т. е.
Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.
4. Смешанное произведение ненулевых векторов 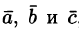
Если 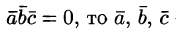
Допустим, что это не так. Можно было бы построить параллелепипед с объемом 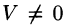
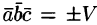
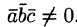
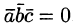
Обратно, пусть векторы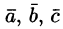
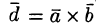
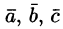
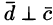
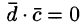
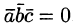
Выражение смешанного произведения через координаты
Пусть заданы векторы 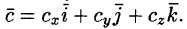
Полученную формулу можно записать короче:
так как правая часть равенства (8.1) представляет собой разложение определителя третьего порядка по элементам третьей строки. Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.
Некоторые приложения смешанного произведения
Определение взаимной ориентации векторов в пространстве
Определение взаимной ориентации векторов 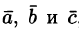
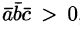
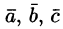
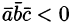
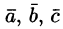
Установление компланарности векторов
Векторы 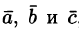
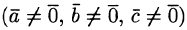
Определение объемов параллелепипеда и треугольной пирамиды
Нетрудно показать, что объем параллелепипеда, построенного на векторах 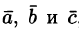
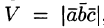
Пример:
Вершинами пирамиды служат точки A(1; 2;3), B(0; -1; 1), С(2;5;2) и D(3;0; -2). Найти объем пирамиды.
Решение:
Находим векторы 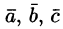
Находим 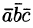
Следовательно,
Определение смешанного произведения, его геометрический смысл
Рассмотрим произведение векторов 

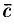
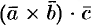
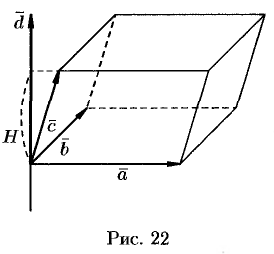
Выясним геометрический смысл выражения 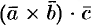


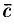
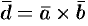
Имеем: 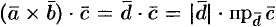
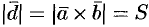
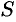
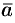

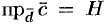
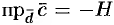
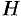
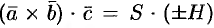
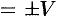
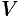


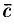
Таким образом, смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если эти векторы образуют правую тройку, и со знаком «минус», если они образуют левую тройку.
Свойства смешанного произведения
1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. 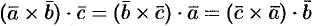
Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер.
2. Смешанное произведение не меняется при перемене местами знаков векторного и скалярного умножения, т. е. 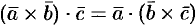
Действительно, 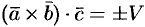
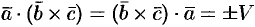


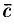

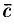

Следовательно, 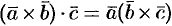
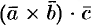
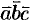
3.Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей, т. е. 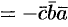
Действительно, такая перестановка равносильна перестановке сомножителей в векторном произведении, меняющей у произведения знак.
4. Смешанное произведение ненулевых векторов 

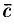
Если 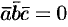


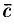
Допустим, что это не так. Можно было бы построить параллелепипед с объемом 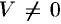
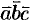
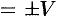
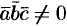
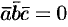
Обратно, пусть векторы 

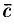
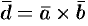


Другие темы по высшей математике возможно вам они будут полезны:
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Задать свой вопрос
*более 50 000 пользователей получили ответ на «Решим всё»
Задача 53620 Дан параллелепипед ABCDA1B1C1D1,…
Условие
5f6c65a2019fbf2dafd19b19
25.09.2020 14:22:51
Дан параллелепипед ABCDA1B1C1D1, построенный на векторах vector{АВ} = (4; 3; 0), vector{AD} = (2; 1; 2) и vector{АА1} = (-3; -2; 5). Найти:
а) объем параллелепипеда;
б) площадь грани ABCD;
математика ВУЗ
4592
Решение
5f3eaa23faf909182968dde0
25.09.2020 15:33:03
★

Написать комментарий
Категория

Математика
Вузовская математика → Аналитическая геометрия → Смешанные
Меню
- Решим всё
- Найти задачу
- Категории
- Статьи
- Тесты
- Архив задач

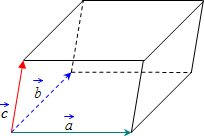
 Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).
Дан параллелепипед ABCDA1B1C1D1, построен на векторах AB(4,3,0), AD(2,1,2) и AA1(-3,-2,5).