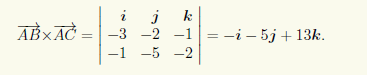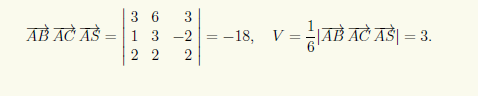Как найти площадь параллелепипеда векторы - Исправление недочетов и поиск решений вместе с Examum.ru

Объем параллелепипеда, построенного на векторах онлайн

Объём параллелепипеда равен смешанному произведению векторов на которых он построен:

Поскольку смешанное произведение векторов, может быть отрицательным числом, а объём геометрического тела — всегда число положительное, то при вычислении объёма параллелепипеда, построенного на векторах, результат смешанного произведения берется по модулю:

Таким образом, для того, чтобы вычислить объём параллелепипеда, построенного на векторах, нужно найти смешанное произведение данных векторов, и полученный результат взять по модулю.

Наш онлайн калькулятор, найдет площадь параллелепипеда с описанием подробного хода решения на русском языке.

Смешанное, векторное и скалярное произведение векторов

Задача:

Дан параллелепипед ABCDA₁B₁C₁D₁, построен на векторах AB(4,3,0), AD(2,1,2) и AA₁(-3,-2,5).
Найти:

Решение:

а) Объем параллелепипеда будем искать через смешанное произведение векторов (AB AD AA₁). Мы знаем, что модуль смешанного произведения векторов равен объему параллелепипеда, построенному на этих векторах.

(AB AD AA₁)

4	3	0
2	1	2
-3	-2	5

20 — 18 + 0 — 0 — 30 + 16

-12

Мы нашли смешанное произведение, ещё надо его взять по модулю и найдём объем параллелепипеда:
V_{ABCDA₁B₁C₁D₁}=12.
б) Площадь, как мы уже знаем, можно искать через векторное произведение векторов. Грань ABCD построена на векторах AB и AD, найдём их векторное произведение. S_ABCD= |[AB AD]|.

[AB AD]

i	j	k
4	3	0
2	1	2

6i — 8j — 2k

Теперь найдём модуль этого вектора:

S_ABCD= \|[AB AD]\|=√	(36+64+4)	=2√(26).

[AD AA₁]

i	j	k
2	1	2
-3	-2	5

9i — 16j — k

S_ADD₁A₁= |[AD AA₁]|=√(81+256+1)=13√2.

в) Что бы найти длину высоты, проведенной из вершины A₁ на грань ABCD, используем формулу для нахождения объема параллелепипеда V=h S_ABCD. С этой формулы видим:

V
S_ABCD

12
2√(26)

6
√(26)

3√(26)
13

г) Косинус угла λ₁, между ребром AB и диагональю B₁D будем высчитывать с помощью скалярного произведения векторов

cos(λ₁)

(AB B₁D)
\|AB\| * \|B₁D\|

Координаты вектора AB мы имеем, от вектор B₁D надо найти. Для этого используем следующую формулу:
B₁D = B₁A₁ + A₁A + AD = — AB — AA₁ + AD₁ = — (4, 3, 0) — (-3, -2, 5) + (2, 1, 2); (Не забывайте, что всё это векторы, надо сложить их соответствующие координаты. )
Сделав вычисления по этой формуле, мы найдём, что вектор B₁D имеет координаты (1, 0, -3). Теперь надо найти длину векторов AB и B₁D:
|AB|=√(16+9+0)=5, |B₁D|=√(1+0+9)=√(10).
Найдём скалярное произведение векторов AB и B₁D, (AB B₁D)=4*1 + 3*0 + 0*(-3)=4.
Теперь, имея все данные мы можем подставить их в нашу формулу:

cos(λ₁)

4
5√(10)

2√(10)
25

д) Что бы найти cos(λ₂), мы используем то, что угол между двумя плоскостями равен углу между перпендикулярами до этих плоскостей. А как мы знаем, векторное произведение — это и есть перпендикуляр до плоскости перемножаемых векторов. Поэтому в роле перпендикуляра к плоскости ADD₁A₁ мы можем взять вектор [AD AA₁], который мы нашли в пункте б), и знаем, что его координаты (9, -16, -1), точно также и для плоскости ABCD — вектор [AB AD] с координатами (6, -8, -2).
Теперь нам остаётся, как в предыдущем варианте найти только косинус угла между двумя векторами, координаты которых нам известны.

cos(λ₂)

69 + (-8)(-16) + (-2)*(-1)
2√(26) * 13√(2)

46√(13)
169

Вот таким не хитрым способом мы и нашли косинус угла между гранями ABCD и ADD₁A₁.

Нахождение площади прямоугольного параллелепипеда: формула и пример

В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.

Формула вычисления площади

Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:

Формула получена следующим образом:

Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a и b;
- четыре боковые грани: со стороной a/b и высотой c.
Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).

Пример задачи

Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.

Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см 2 .

источники:

http://matemonline.com/primeru/zada4a-na-vektor/

Нахождение площади прямоугольного параллелепипеда: формула и пример

Источник

Вычисление площадей многоугольников и объемов многогранников, заданных координатами своих вершин в прямоугольной системе координат, основывается на использовании скалярного, векторного и смешанного произведений векторов.

Если параллелограмм задан в пространстве координатами своих вершин, то для вычисления его площади нужно найти координаты двух векторов, соответствующих смежным сторонам параллелограмма, а затем модуль их векторного произведения. Аналогично вычисляется площадь треугольника, равная половине модуля векторного произведения векторов, на которых он построен как на смежных сторонах.

Пример 4.2. Пусть три вершины треугольника заданы своими координатами: A(4;4;4), B(1; 2; 3), C(3; —1;2).

Для определения площади ΔABC с помощью (4.10) найдем координаты векторов AB и AC: AB = {1 — 4; 2 — 4; 3 — 4} = { — 3; —2; —1}, —1 = {3 — 4; —1 — 4; 2 — 4} = { — 1; —5; —2}.

Затем по (3.2) вычислим их векторное произведение:

Модуль этого векторного произведения равен |AB×AC| = √((—1)² + (—5)² + 13²) = √195, и следовательно, S ΔABC = |AB×AC|/2 = √195/2 #

Для вычисления объема параллелепипеда, заданного координатами своих вершин, нужно найти координаты трех векторов, соответствующих смежным ребрам, а затем вычислить модуль смешанного произведения этих векторов. Через смешанное произведение вычисляется и объем произвольной треугольной пирамиды SABC (см. пример 3.2), поскольку он равен 1/6 объема параллелепипеда, построенного на ребрах AB, AC и AS. Таким образом, объем этой пирамиды равен VSABC = |ABACAS|/6.

Пример 4.3. Найдем объем V пирамиды SABC, заданной координатами своих вершин: A(2; —1;1), B(5; 5; 4), C(3; 2; —1), S(4;1;3).

Используя (4.10), вычисляем координаты векторов, направленных по ребрам пирамиды: AB = {5 — 2; 5 — (—1);4 — 1} = {3; 6; 3}, AC = {3 — 2; 2 — (—1); —1 — 1} = {1;3; —2},= AS {4 — 2;1 — (—1); 3 — 1} = {2;2;2}, и определяем объем с помощью смешанного произведения найденных векторов:

Источник

Векторным
произведением
[a

b]
векторов a
и b
называется вектор c,
который равен определителю, в первой
строке которого стоят стандартные
базисные орты, а во второй и третьей
строке координаты векторов-сомножителей

(57)

Векторное
произведение обозначается также [ab]
или a

b.

Свойства векторного
произведения:

1.
[a

b]
= [b

a]
в отличие от скалярного произведения,
векторное произведение антикоммутативно.

2.
[a

b]
= [a

b]
= [ab]
числовой множитель можно выносить за
знак векторного произведения.

3.
[a

(b
+
с)]
= [a

b]
+
[a

с]
для векторного произведения справедлив
распределительный (дистрибутивный)
закон

4
.
[a

b]
= 0
тогда и только тогда, когда векторы a
и b
параллельны.
В частности, [a

0]
= 0
a
(т. о., нуль-вектор параллелен любому
вектору).

С
войства
14
векторного произведения есть очевидные
следствия свойств определителей,
приведенных в пункте 3.3. Так свойство 1
следует из свойства 4 п. 3.3, свойство 2 
из свойства 2 п. 3.3 и т. д.

Можно
показать, что модуль векторного
произведения не изменяется при переходах
от одного ортонормированного базиса к
другому. Направление векторного
произведения изменится на противоположное,
если один из векторов базиса изменит
направление на противоположное.

Подобно
скалярному, векторному произведению
можно дать геометрическое,
то есть, не зависящее от выбора системы
координат, определение.
Векторным
произведением
[a

b]
векторов a
и b
называется вектор c,
который:

1)
перпендикулярен плоскости векторов a
и b;

2)
направлен так, что если смотреть из его
конца, то для совмещения сомножителей
первый сомножитель ко второму следует
поворачивать против часовой стрелки;

3)
модуль векторного произведения равен
площади параллелограмма, построенного
на векторах-сомножителях, т. е. произведению
длин векторов-сомножителей на синус
угла между ними:

|[a

b]|=
|a|
|b|sin, (58)

в
частности, модуль векторного произведения
взаимно перпендикулярных векторов
равен произведению длин векторов-сомножителей.

Легко
убедиться, что орты стандартного базиса
связаны соотношением

[i

j]
= k.
Такие системы координат (базисы), третий
орт которых есть векторное произведение
первого орта на второй, называются
левоориентированными или просто левыми,
если же [i

j]
= 
k,
то такие системы координат (базисы)
называются правоориентированными или
же правыми. При переходах между базисами
различной ориентации векторное
произведение меняет направление на
противоположное (меняет знак).

Векторное
произведение естественно использовать
в задачах, связанных с вычислением
площадей. Как следует из (57) и (58), площадь
параллелограмма, построенного на
векторах a
и b
равна:

|[ab]|=

. (60)

6.6.1. Смешанное произведение и вычисление объемов

Умножим
векторное произведение векторов a
и b
скалярно на некоторый третий вектор с:
(с[a

b])

такое произведение трех векторов
называется скалярно-векторным или
смешанным
произведением

. (61)

Сумма,
стоящая в правой части (61), получилась
как сумма попарных произведений
координат сомножителей, с учетом того,
что координаты [a

b]
есть коэффициенты при i,
j,
k
в выражении
(57). Правая часть (61) есть правая часть
(57), в которой векторы i,
j,
k
заменили
координатами вектора с:
c_x,
c_y,
c_z_.
Значит правая часть выражения (61)
представляет собой разложение по
элементам первой строки определителя

. (62)

Смешанное
произведение трех векторов равно
определителю, по строкам которого стоят
координаты векторов в том порядке, как
они записаны в смешанном произведении.

Смешанное
произведение наследует общие свойства
векторного и скалярного произведения,
а именно:

 множитель,
стоящий перед любым из сомножителей,
можно выносить за знак смешанного
произведения;

 смешанное
произведение дистрибутивно: «произведение
суммы равно сумме произведений», т. е.
если один из сомножителей представлен
в виде суммы, то смешанное произведение
равно сумме соответствующих смешанных
произведений, например: (с
[a
+
d

b])
= (с
[a

b])
+ (с
[d

b])

 модуль
смешанного произведения трех взаимно
ортогональных векторов равен произведению
их длин (проверьте!);

 если
поменять местами любые два сомножителя,
смешанное произведение сменит знак
(очевидное следствие свойств определителей).

В
ыясним
вопрос о геометрическом смысле смешанного
произведения. Пусть для наглядности
сомножители a
и b,
входящие в векторное произведение,
расположены в плоскости xOу,
а вектор c
расположен под некоторым углом к
плоскости xOу
(см. рис.12).
Тогда векторное произведение [a

b]
параллельно оси z,
а величина смешанного произведения
равна произведению |[a

b]|
на проекцию вектора с
на вектор [a

b],
т. е. на ось z:
|(с[a

b])|
= |[a

b]|Пр_zс.
Если построить на векторах a,b,c
параллелепипед, то Пр_zс
будет его высотой, а |[a

b]|

площадью параллелограмма, лежащего в
основании. Но произведение площади
основания на высоту есть объем
параллелепипеда. Таким образом, модуль
смешанного произведения равен объему
параллелепипеда, построенного на
векторах-сомножителях.

Полученный
нами результат допускает обобщение. В
самом деле, если векторы a
и b
расположены в плоскости xOу,
то, учитывая, что a_z=
b_z= 0,
площадь параллелограмма, построенного
на этих векторах, равна^⁸⁰:

|[ab]|
=

.

Значит,
объем трехмерного параллелепипеда,
построенного на трех векторах, равен
модулю определителя, по строкам которого
стоят координаты трех образующих
векторов, а объем (площадь) двумерного
параллелепипеда (параллелограмма),
построенного на двух векторах, равен
модулю аналогично сконструированного
определителя второго порядка. Естественное
обобщение: геометрический
смысл модуля определителя n-го
порядка 
это объем n-мерного
параллелепипеда, построенного на строках
(столбцах) определителя.
Знак определителя позволяет различать
«левые» и «правые» ориентации систем
векторов^⁸¹.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Ориентированные площади и объёмы

Ориентированная площадь параллелограмма

Ориентированной площадью $S_{astvec{a},vec{b}}^{land}$ параллелограмма, построенного на неколлинеарных векторах vec{a} и vec{b} , называется его площадь $S_{astvec{a},vec{b}}$ , взятая со знаком плюс, если ориентация пары векторов vec{a} и vec{b} правая $bigl(S_{astvec{a},vec{b}}^{land}=S_{astvec{a},vec{b}}bigr)$ , и со знаком минус, если ориентация — левая $bigl(S_{astvec{a},vec{b}}^{land}=-S_{astvec{a},vec{b}}bigr)$

Внешним (косым) произведением неколлинеарных векторов vec{a} и vec{b} на плоскости называется число, равное ориентированной площади $S_{astvec{a},vec{b}}^{land}$ параллелограмма, построенного на этих векторах. Если векторы vec{a} и vec{b} коллинеарны, то их внешнее произведение считается равным нулю. Внешнее произведение обозначается $S_{astvec{a},vec{b}}^{land}=vec{a}landvec{b}$ . Его свойства повторяют алгебраические свойства векторного произведения, т.е. для любых векторов vec{a},vec{b},vec{c} на плоскости и любого числа lambda справедливы равенства:

1) vec{a}landvec{b}=-vec{b}landvec{a} ;

2) (vec{a}+vec{b})landvec{c}=vec{a}landvec{c}+vec{b}landvec{c} ;

3) (lambdacdotvec{a})landvec{b}=lambdacdot(vec{a}landvec{b}) .

4) Если векторы vec{a} и vec{b} в правом ортонормированием базисе vec{i},vec{j} имеют координаты x_a,y_a и x_b,y_b соответственно, то внешнее произведение этих векторов находится по формуле

$S_{astvec{a}, vec{b}}^{land}= begin{vmatrix} x_a&x_b\y_a&y_bend{vmatrix}=begin{vmatrix}x_a&y_a\x_b&y_bend{vmatrix}=x_acdot y_b-x_bcdot y_a,.$

(1.18)

Если $a=begin{pmatrix} x_a&y_a end{pmatrix}^T,~ b=begin{pmatrix}x_b&y_bend{pmatrix}^T$ — координатные столбцы векторов vec{a},vec{b} в стандартном базисе на плоскости, то их внешнее произведение находится по формуле

$S_{astvec{a},vec{b}}^{land}=vec{a}landvec{b}=begin{vmatrix}x_a&y_aend{vmatrix}!cdot!begin{vmatrix}0&1\-1&0end{vmatrix}!cdot!begin{pmatrix}x_b\y_bend{pmatrix}.$

Приведенные свойства внешнего произведения следуют из алгебраических свойств векторного произведения, если векторы vec{a},vec{b},vec{c} на плоскости рассматривать как векторы в пространстве с нулевыми аппликатами.

Рассмотрим задачу разложения вектора vec{a} по базису $vec{e}_1,vec{e}_2$ на плоскости. Отложим все векторы от произвольной точки . Сначала разберем случаи, когда векторы vec{a} и $vec{e}_1$ коллинеарны: одинаково направлены (рис.1.49,а) или противоположно направлены (рис. 1.49,6). В этих случаях ордината x_2 вектора vec{a} равна нулю, а абсцисса находится как отношение

Разложение векторов по базису на плоскости

$x_1=frac{vec{a}}{vec{e}_1}=frac{S_{astvec{a},vec{e}_2}}{S_{astvec{e}_1,vec{e}_2}}=frac{vec{a}landvec{e}_2}{vec{e}_1landvec{e}_2}$ при $vec{a}uparrowuparrowvec{e}_1$ (рис.1.49,а)

$x_1=frac{vec{a}}{vec{e}_1}=frac{S_{astvec{a},vec{e}_2}}{S_{astvec{e}_1,vec{e}_2}}=frac{vec{a}landvec{e}_2}{vec{e}_1landvec{e}_2}$ при $vec{a}uparrowdownarrowvec{e}_1$ (рис.1.49,b)

так как пара $vec{a},vec{e}_2$ в первом случае правая (рис.1.49,а), а во втором случае — левая (рис.1.49,б).

Пусть теперь векторы vec{a} и $vec{e}_1$ не коллинеарны (рис.1.49,в). Построим проекции $vec{a}_1$ и $vec{a}_2$ на прямые, содержащие базисные векторы: $vec{a}=vec{a}_1+vec{a}_2$ . Из концов векторов $vec{a}_1$ и $vec{e}_1$ опустим перпендикуляры h_1 и соответственно на прямую, содержащую вектор $vec{e}_2$ . Учитывая, что векторы $vec{a}_1$ и $vec{e}_1$ противоположно направлены, а также подобие прямоугольных треугольников с гипотенузами $vec{a}_1$ и $vec{e}_1$ , находим абсциссу x_1 вектора vec{a} :

$x_1=frac{vec{a}_1}{vec{e}_1}=-frac{h_1}{h}=-frac{S_{astvec{a},vec{e}_2}}{S_{astvec{e}_1,vec{e}_2}}=frac{vec{a}landvec{e}_2}{vec{e}_1landvec{e}_2}.$

так как пара $vec{e}_1,vec{e}_2$ — правая, а пара $vec{a},vec{e}_2$ — левая. Аналогично находится ордината (векторы $vec{a}_2$ и $vec{e}_2$ одинаково направлены)

$x_2=frac{vec{a}_2}{vec{e}_2}=frac{S_{astvec{a},vec{e}_1}}{S_{astvec{e}_1,vec{e}_2}}=frac{vec{e}_1landvec{a}}{vec{e}_1landvec{e}_2}.$

Таким образом, вектор vec{a} имеет следующее разложение по базису $vec{e}_1,vec{e}_2$ на плоскости:

$vec{a}=x_1cdotvec{e}_1+x_2cdotvec{e}_2,quad text{where}quad x_1=frac{vec{a}landvec{e}_2}{vec{e}_1landvec{e}_2},~x_2=frac{vec{e}_1landvec{a}}{vec{e}_1landvec{e}_2}.$

(1.19)

Рассмотрим применение формулы (1.19) для решения системы двух линейных уравнений с двумя неизвестными:

$begin{cases}a_1cdot x_1+b_1cdot x_2=c_1,\[2pt]a_2cdot x_1+b_2cdot x_2=c_2.end{cases}$

Эту систему можно записать в виде $begin{pmatrix}c_1\c_2end{pmatrix}=x_1begin{pmatrix}a_1\a_2end{pmatrix}+x_2begin{pmatrix}b_1\b_2end{pmatrix}$ .Рассматривая полученные столбцы как координатные столбцы векторов vec{c},vec{a},vec{b} в стандартном базисе на плоскости, получаем разложение $vec{c}=x_1{cdot}vec{a}+x_2{cdot}vec{b}$ .

Таким образом, нахождение решения системы уравнений свелось к задаче разложения вектора vec{c} по векторам vec{a} и vec{b} . Предполагая, что коэффициенты при неизвестных не пропорциональны, т.е. a_1:b_1ne a_2:b_2 (векторы vec{a} и vec{b} не коллинеарны), по формуле (1.19), полагая $vec{a}=vec{c},~vec{e}_1=vec{a},~vec{e}_2=vec{b}$ , получаем:

$x_1=frac{vec{c}landvec{b}}{vec{a}landvec{b}}=dfrac{begin{vmatrix}c_1&b_1\c_2&b_2end{vmatrix}}{begin{vmatrix}a_1&b_1\a_2&b_2end{vmatrix}};qquad x_2=frac{vec{a}landvec{c}}{vec{a}landvec{b}}=dfrac{begin{vmatrix}a_1&c_1\a_2&c_2end{vmatrix}}{begin{vmatrix}a_1&b_1\a_2&b_2end{vmatrix}}$ что совпадает с правилом Крамера.

Ориентированный объем параллелепипеда

Ориентированным объемом $V_{astvec{a},vec{b},vec{c}}^{land}$ параллелепипеда, построенного на некомпланарных векторах , называется его объем $V_{astvec{a},vec{b},vec{c}}$ , взятый со знаком плюс, если ориентация тройки векторов правая $V_{astvec{a},vec{b},vec{c}}^{land}=V_{astvec{a},vec{b},vec{c}}$ и со знаком минус, если ориентация — левая $V_{astvec{a},vec{b},vec{c}}^{land}=-V_{astvec{a},vec{b},vec{c}}$ .

Внешним (косым) произведением некомпланарных векторов vec{a},vec{b},vec{c} называется число, равное ориентированному объему $V_{astvec{a},vec{b},vec{c}}^{land}$ параллелепипеда, построенного на этих векторах. Если векторы компланарны, то их внешнее произведение считается равным нулю. Внешнее произведение обозначается $V_{astvec{a},vec{b},vec{c}}^{land}=vec{a}landvec{b}landvec{c}$ .

Внешнее произведение трех векторов совпадает с их смешанным произведением (в силу первого геометрического свойства смешанного произведения), т.е. $V_{astvec{a},vec{b},vec{c}}^{land}=vec{a}landvec{b}landvec{c}=bigl(vec{a},vec{b},vec{c}bigr)$ . В ортонормированием базисе

$V_{astvec{a}, vec{b},vec{c}}^{land}= vec{a}land vec{b}landvec{c}=begin{vmatrix}x_a&x_b&x_c\y_a&y_b&y_c\z_a&z_b&z_cend{vmatrix}=begin{vmatrix}x_a&y_a&z_a\x_b&y_b&z_b\x_c&y_c&z_cend{vmatrix}=bigl(vec{a},vec{b},vec{c}bigr),$

(1.20)

так как определитель транспонированной матрицы равен определителю исходной матрицы.

При помощи ориентированных объемов задача разложения вектора vec{a} по базису $vec{e}_1,vec{e}_2,vec{e}_3$ в пространстве решается так же как и на плоскости с использованием ориентированных площадей. В результате получаем

$vec{a}= x_1cdot vec{e}_1+ x_2cdot vec{e}_2+ x_3cdot vec{e}_3,$

(1.21)

где $x_1=frac{(vec{a},vec{e}_2,vec{e}_3)}{(vec{e}_1, vec{e}_2, vec{e}_3)};~~ x_2=frac{(vec{e}_1,vec{a},vec{e}_3)}{(vec{e}_1, vec{e}_2,vec{e}_3)};~~ x_3=frac{(vec{e}_1,vec{e}_2,vec{a})}{(vec{e}_1, vec{e}_2,vec{e}_3)}$

Формула (1.21) соответствует правилу Крамера решения системы трех линейных уравнений с тремя неизвестными.

Пример 1.23. Заданы координатные столбцы

$a=begin{pmatrix}1\0\0end{pmatrix}!,qquad b=begin{pmatrix} 1\1\0end{pmatrix}!,qquad c=begin{pmatrix} 0\1\1end{pmatrix}!,qquad d=begin{pmatrix}1\2\3end{pmatrix}.$

векторов vec{a},vec{b},vec{c},vec{d} в стандартном базисе. Разложить вектор vec{d} по векторам .

Решение. По формуле (1.20) находим смешанные произведения

$bigl(vec{a},vec{b},vec{c}bigr),=begin{vmatrix}1&1&0\0&1&1\0&0&1end{vmatrix}=1;~bigl(vec{d},vec{b},vec{c}bigr),=begin{vmatrix}1&1&0\2&1&1\3&0&1end{vmatrix}=2;~bigl(vec{a},vec{d},vec{c}bigr),=begin{vmatrix}1&1&0\0&2&1\0&3&1end{vmatrix}=-1;~bigl(vec{a},vec{b},vec{d}bigr),=begin{vmatrix}1&1&1\0&1&2\0&0&3end{vmatrix}=3.$

Коэффициенты разложения определяем по формуле (1.21):

$x_1=frac{(vec{d},vec{b},vec{c})}{(vec{a},vec{b},vec{c})}=frac{2}{1}=2;qquad x_2=frac{(vec{a},vec{d},vec{c})}{(vec{a},vec{b},vec{c})}=frac{-1}{1}=-1;qquad x_3=frac{(vec{a},vec{b},vec{d})}{(vec{a},vec{b},vec{c})}=frac{3}{1}=3.$

Следовательно, vec{d}=2,vec{a}-vec{b}+3,vec{c} .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Задача:

Дан параллелепипед ABCDA₁B₁C₁D₁, построен на векторах AB(4,3,0), AD(2,1,2) и AA₁(-3,-2,5).
Найти:

а) объем параллелепипеда;

б) площадь граней ABCD и ADD₁A₁;

в) длину высоты, проведенной из вершины A₁ на грань ABCD;

г) косинус угла λ₁, между ребром AB и диагональю B₁D;

д) косинус угла λ₂, между гранями ABCD и ADD₁A₁.

Решение:

а) Объем параллелепипеда будем искать через смешанное произведение векторов (AB AD AA₁). Мы знаем, что модуль смешанного произведения векторов равен объему параллелепипеда, построенному на этих векторах.

(AB AD AA₁) =

4 3 0

2 1 2

-3 -2 5

= 20 — 18 + 0 — 0 — 30 + 16 = -12 .

Мы нашли смешанное произведение, ещё надо его взять по модулю и найдём объем параллелепипеда:
V_{ABCDA₁B₁C₁D₁}=12.
б) Площадь, как мы уже знаем, можно искать через векторное произведение векторов. Грань ABCD построена на векторах AB и AD, найдём их векторное произведение. S_ABCD= |[AB AD]|.

[AB AD] =

i j k

4 3 0

2 1 2

= 6i — 8j — 2k ,

Теперь найдём модуль этого вектора:

S_ABCD= |[AB AD]|=√ (36+64+4) =2√(26).

Точно также и для грани ADD₁A₁. S_ADD₁A₁= |[AD AA₁]|.

[AD AA₁] =

i j k

2 1 2

-3 -2 5

= 9i — 16j — k ,

S_ADD₁A₁= |[AD AA₁]|=√(81+256+1)=13√2.
в) Что бы найти длину высоты, проведенной из вершины A₁ на грань ABCD, используем формулу для нахождения объема параллелепипеда V=h S_ABCD. С этой формулы видим:

h =

V

S_ABCD

=

12

2√(26)

=

6

√(26)

=

3√(26)

13

.
г) Косинус угла λ₁, между ребром AB и диагональю B₁D будем высчитывать с помощью скалярного произведения векторов

cos(λ₁) =

(AB B₁D)

|AB| * |B₁D|

.

Координаты вектора AB мы имеем, от вектор B₁D надо найти. Для этого используем следующую формулу:
B₁D = B₁A₁ + A₁A + AD = — AB — AA₁ + AD₁ = — (4, 3, 0) — (-3, -2, 5) + (2, 1, 2); (Не забывайте, что всё это векторы, надо сложить их соответствующие координаты!!!)
Сделав вычисления по этой формуле, мы найдём, что вектор B₁D имеет координаты (1, 0, -3). Теперь надо найти длину векторов AB и B₁D:
|AB|=√(16+9+0)=5, |B₁D|=√(1+0+9)=√(10).
Найдём скалярное произведение векторов AB и B₁D, (AB B₁D)=4*1 + 3*0 + 0*(-3)=4.
Теперь, имея все данные мы можем подставить их в нашу формулу:

cos(λ₁) =

4

5√(10)

=

2√(10)

25

.
д) Что бы найти cos(λ₂), мы используем то, что угол между двумя плоскостями равен углу между перпендикулярами до этих плоскостей. А как мы знаем, векторное произведение — это и есть перпендикуляр до плоскости перемножаемых векторов. Поэтому в роле перпендикуляра к плоскости ADD₁A₁ мы можем взять вектор [AD AA₁], который мы нашли в пункте б), и знаем, что его координаты (9, -16, -1), точно также и для плоскости ABCD — вектор [AB AD] с координатами (6, -8, -2).
Теперь нам остаётся, как в предыдущем варианте найти только косинус угла между двумя векторами, координаты которых нам известны.

cos(λ₂) =

6*9 + (-8)*(-16) + (-2)*(-1)

2√(26) * 13√(2)

=

46√(13)

169

.

Вот таким не хитрым способом мы и нашли косинус угла между гранями ABCD и ADD₁A₁.

Материалы по теме:

Cкалярное произведение и косинус угла между векторами
Ответ на 10 вопросов связанных с задачами на векторы…
Находим скалярное произведение и угол между векторами…
Векторное произведение

Загрузка…

Источник