Как найти площадь параллелограмма если известен треугольник

Как найти площадь параллелограмма, треугольника, трапеции

Любовь Петровна Гаврилюк

Эксперт по предмету «Геометрия»

Задать вопрос автору статьи

Площадь параллелограмма

Теорема 1

Площадь параллелограмма определяется как произведение длины его стороны, на высоту, проведенную к ней.

Математически это можно записать следующим образом

[S=ah]

где $a$ сторона параллелограмма, $h$ — высота, проведенная к этой стороне.

Доказательство.

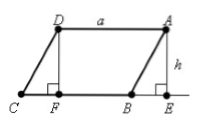
Пусть нам дан параллелограмм $ABCD$, у которого $AD=BC=a$. Проведем высоты $DF$ и $AE$ (рис. 1).

Рисунок 1.

Очевидно, что фигура $FDAE$ — прямоугольник.

[angle BAE={90}^0-angle A, ] [angle CDF=angle D-{90}^0={180}^0-angle A-{90}^0={90}^0-angle A=angle BAE]

Следовательно, так как $CD=AB, DF=AE=h$, по $I$ признаку равенства треугольников $triangle BAE=triangle CDF$. Тогда

[S_{FDAE}=S_{ABCD}-S_{CDF}+S_{BAE}=S_{ABCD}-S_{CDF}+S_{CDF}=S_{ABCD}]

Значит по теореме о площади прямоугольника:

[S_{ABCD}=S_{FDAE}=ah]

Теорема доказана.

Теорема 2

Площадь параллелограмма определяется как произведение длины его смежных сторон, на синус угла между этими сторонами.

Математически это можно записать следующим образом

[S=absinalpha ]

где $a, b$ стороны параллелограмма, $alpha $ — угол между ними.

Доказательство.

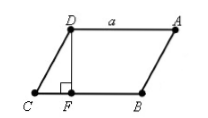
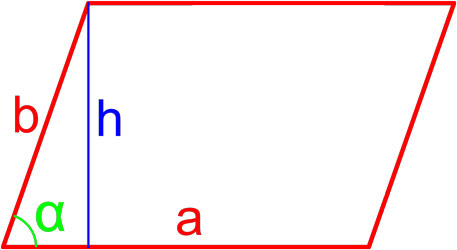
Пусть нам дан параллелограмм $ABCD$, у которого $BC=a, CD=b, angle C=alpha $. Проведем высоту $DF=h$ (рис. 2).

Рисунок 2.

По определению синуса, получим

[sinalpha =frac{DF}{CD}=frac{h}{b}]

Следовательно

[h=bsinalpha ]

Значит, по теореме $1$:

[S=ah=absinalpha ]

Теорема доказана.

Площадь треугольника

Теорема 3

Площадь треугольника определяется как половина произведения длины его стороны, на высоту, проведенную к ней.

Математически это можно записать следующим образом

[S=frac{1}{2}ah]

где $a$ сторона треугольника, $h$ — высота, проведенная к этой стороне.

Доказательство.

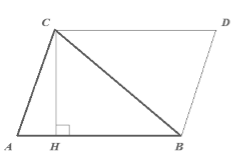
Пусть нам дан треугольник $ABC$, у которого $AB=a$. Проведем высоту $CH=h$. Достроим его до параллелограмма $ABCD$ (рис. 3).

Рисунок 3.

Очевидно, что по $I$ признаку равенства треугольников $triangle ACB=triangle CDB$. Тогда

[S_{ABC}=frac{1}{2}S_{ABCD}]

Значит по теореме $1$:

[S_{ABC}=frac{1}{2}ah]

Теорема доказана.

«Как найти площадь параллелограмма, треугольника, трапеции» 👇

Теорема 4

Площадь треугольника определяется как половина произведения длины его смежных сторон, на синус угла между этими сторонами.

Математически это можно записать следующим образом

[S=frac{1}{2}absinalpha ]

где $a, b$ стороны треугольника, $alpha $ — угол между ними.

Доказательство.

Пусть нам дан треугольник $ABC$, у которого $AB=a$. Проведем высоту $CH=h$. Достроим его до параллелограмма $ABCD$ (рис. 3).

Очевидно, что по $I$ признаку равенства треугольников $triangle ACB=triangle CDB$. Тогда

[S_{ABC}=frac{1}{2}S_{ABCD}]

Значит по теореме $1$:

[S_{ABC}=frac{1}{2}absinalpha ]

Теорема доказана.

Площадь трапеции

Теорема 5

Площадь трапеции определяется как половина произведения суммы длин его оснований, на его высоту.

Математически это можно записать следующим образом

[S=frac{1}{2}(a+b)h]

Доказательство.

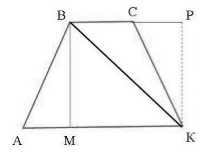
Пусть нам дана трапеция $ABCK$, где $AK=a, BC=b$. Проведем в ней высоты $BM=h$ и $KP=h$, а также диагональ $BK$ (рис. 4).

Рисунок 4.

[S_{ABCK}=S_{ABK}+S_{BCK}]

По теореме $3$, получим

[S_{ABK}=frac{1}{2}AKcdot BM=frac{1}{2}ah, S_{BCK}=frac{1}{2}BCcdot KP=frac{1}{2}bh]

Тогда

[S_{ABCK}=frac{1}{2}ah+frac{1}{2}bh=frac{1}{2}(a+b)h]

Теорема доказана.

Пример задачи

Пример 1

Найти площадь равностороннего треугольника, если длина его стороны равняется $a.$

Решение.

Так как треугольник равносторонний, то все его углы равняются ${60}^0$.

Тогда, по теореме $4$, имеем

[S=frac{1}{2}acdot acdot sin{60}^0=frac{a^2sqrt{3}}{4}]

Ответ: $frac{a^2sqrt{3}}{4}$.

Заметим, что результат этой задачи можно применять при нахождении площади любого равностороннего треугольника с данной стороной.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 19.05.2023

Определение параллелограмма

Параллелограмм — это четырехугольник, в котором противоположные стороны равны и параллельны.

Онлайн-калькулятор площади параллелограмма

Параллелограмм обладает некоторыми полезными свойствами, которые упрощают решение задач, связанных с этой фигурой. Например, одно из свойств заключается в том, что противоположные углы параллелограмма равны.

Рассмотрим несколько способов и формул с последующим решением простых примеров.

Формула площади параллелограмма по основанию и высоте

Данный способ нахождения площади является, наверно, одним из основных и простых, так как он практически идентичен формуле по нахождению площади треугольника за небольшим исключением. Для начала разберем обобщенный случай без использования чисел.

Пусть дан произвольный параллелограмм с основанием aa, боковой стороной bb и высотой hh, проведенной к нашему основанию. Тогда формула для площади этого параллелограмма:

S=a⋅hS=acdot h

aa — основание;
hh — высота.

Разберем одну легкую задачу, чтобы потренироваться в решении типовых задач.

Пример

Найти площадь параллелограмма, в котором известно основание, равное 10 (см.) и высота, равная 5 (см.).

Решение

a=10a=10
h=5h=5

Подставляем в нашу формулу. Получаем:
S=10⋅5=50S=10cdot 5=50 (см. кв.)

Ответ: 50 (см. кв)

Формула площади параллелограмма по двум сторонам и углу между ними

В этом случае искомая величина находится так:

S=a⋅b⋅sin⁡(α)S=acdot bcdotsin(alpha)

a,ba, b — стороны параллелограмма;
αalpha — угол между сторонами aa и bb.

Теперь решим другой пример и воспользуемся вышеописанной формулой.

Пример

Найти площадь параллелограмма если известна сторона aa, являющаяся основанием и с длиной 20 (см.) и периметр pp, численно равный 100 (см.), угол между смежными сторонами (aa и bb) равен 30 градусам.

Решение

a=20a=20
p=100p=100
α=30∘alpha=30^{circ}

Для нахождения ответа нам неизвестна лишь вторая сторона данного четырехугольника. Найдем ее. Периметр параллелограмма дается формулой:
p=a+a+b+bp=a+a+b+b
100=20+20+b+b100=20+20+b+b
100=40+2b100=40+2b
60=2b60=2b
b=30b=30

Самое сложное позади, осталось только подставить наши значения для сторон и угла между ними:
S=20⋅30⋅sin⁡(30∘)=300S=20cdot 30cdotsin(30^{circ})=300 (см. кв.)

Ответ: 300 (см. кв.)

Формула площади параллелограмма по диагоналям и углу между ними

S=12⋅D⋅d⋅sin⁡(α)S=frac{1}{2}cdot Dcdot dcdotsin(alpha)

DD — большая диагональ;
dd — малая диагональ;
αalpha — острый угол между диагоналями.

Пример

Даны диагонали параллелограмма, равные 10 (см.) и 5 (см.). Угол между ними 30 градусов. Вычислить его площадь.

Решение

D=10D=10
d=5d=5
α=30∘alpha=30^{circ}

S=12⋅10⋅5⋅sin⁡(30∘)=12.5S=frac{1}{2}cdot 10 cdot 5 cdotsin(30^{circ})=12.5 (см. кв.)

Ответ: 12.5 (см. кв.)

Решение контрольной работы по геометрии онлайн — от профильных экспертов Студворк!

Тест по теме «Площадь параллелограмма»

Формулы площадей фигур

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формулы площади треугольника

Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.

где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.

Формула площади треугольника по трем сторонам

Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .

S = p p — a p — b p — c ,

где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.

Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

S = 1 2 a · b · sin γ ,

где a, b — стороны треугольника,
γ — угол между сторонами a и b .

Формула площади треугольника по трем сторонам и радиусу описанной окружности

a, b, c — стороны треугольника,
R — радиус описанной окружности.

Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2

Формулы площади квадрата

Формула площади квадрата по длине стороны

Площадь квадрата равна квадрату длины его стороны.

где S — площадь квадрата,
a — длина стороны квадрата.

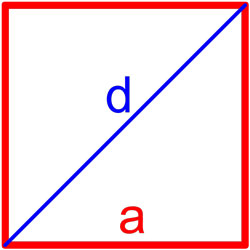
Формула площади квадрата по длине диагонали

Площадь квадрата равна половине квадрата длины его диагонали.

где S — площадь квадрата,
d — длина диагонали квадрата.

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон.

где S — площадь прямоугольника,
a, b — длины сторон прямоугольника.

Формулы площади параллелограмма

Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.

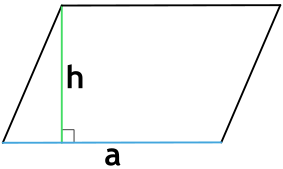
Формула площади параллелограмма по длине стороны и высоте

Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

где S — площадь параллелограмма,
a, h — длины сторон параллелограмма.

Формула площади параллелограмма по двум сторонам и углу между ними

Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

где S — площадь параллелограмма,
a, b — длины сторон параллелограмма,
α — угол между сторонами параллелограмма.

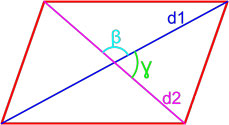
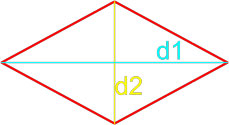
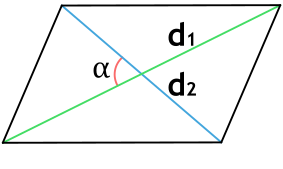
Формула площади параллелограмма по двум диагоналям и углу между ними

Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

S = d1 · d2 · sin β 2 = d1 · d2 · sin γ 2 ,

где S — площадь параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
β , γ — угол между диагоналями параллелограмма.

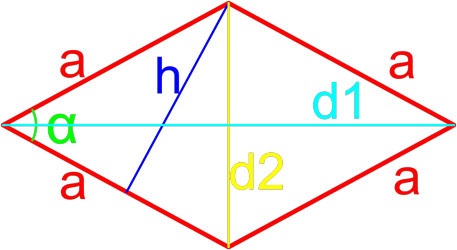
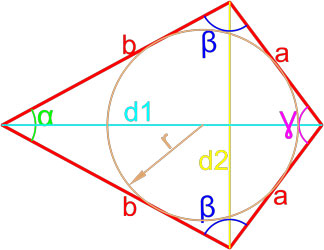
Формулы площади ромба

Формула площади ромба по длине стороны и высоте

Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

где S — площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба.

Формула площади ромба по длине стороны и углу

Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

где S — площадь ромба,
a — длина стороны ромба,
α — угол между сторонами ромба.

Формула площади ромба по длинам его диагоналей

Площадь ромба равна половине произведению длин его диагоналей.

где S — площадь ромба,
d1, d2 — длины диагоналей ромба.

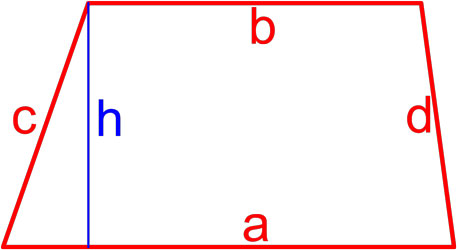
Формулы площади трапеции

Трапеция — это четырёхугольник, у которого две ( a, b ) стороны параллельны (основания), а две другие ( c, d ) стороны не параллельны (боковые стороны).

Формула Герона для трапеции

где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p = a + b + c + d 2 — полупериметр трапеции.

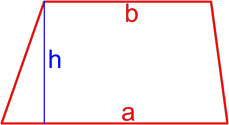
Формула площади трапеции по длине основ и высоте

Площадь трапеции равна произведению полусуммы её оснований на высоту.

где S — площадь трапеции,
a, b — длины основ трапеции,
h — высота трапеции.

Формулы площади дельтоида

Дельтоид — это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.

Формула площади дельтоида по двум неравным сторонам и углу между ними

Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.

где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
β — угол между неравными сторонами дельтоида.

Формула площади дельтоида по равным сторонам и углу между ними

Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.

S = a 2 sin γ + b 2 sin α 2 ,

где S — площадь дельтоида,
a, b — длины сторон дельтоида,
α — угол между равными сторонами b ,
γ — угол между равными сторонами a .

Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности

Площадь дельтоида равна произведению суммы неравных сторон на радиус вписанной окружности.

где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
r — радиус вписанной окружности.

Формула площади дельтоида по двум диагоналям

Площадь дельтоида равна половине произведения длин двух диагоналей.

где S — площадь дельтоида,
d1, d2 — диагонали дельтоида.

Формулы площади произвольного выпуклого четырехугольника

Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними

Площадь произвольного выпуклого выпуклого четырехугольника равна половине произведения его диагоналей умноженной на синус угла между ними.

S = d1 · d2 · sin γ 2 ,

где S — площадь четырехугольника,
d1, d2 — диагонали четырехугольника,
γ — любой из четырёх углов между диагоналями.

Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника,
θ = α + β 2 — полусумма двух противоположных углов четырехугольника.

Формула площади вписанного четырехугольника (формула Брахмагупты)

Если вокруг четырехугольника можно описать окружность, то его площадь равна

S = p — a p — b p — c p — d ,

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника.

Формула площади четырехугольника с вписанной окружностью

Если в четырехугольник можно вписать окружность, то его площадь равна:

где S — площадь четырехугольника,
r — радиус вписанной окружности,
p = a + b + c + d 2 — полупериметр четырехугольника.

Формула площади четырехугольника с вписанной и описанной окружностями

Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна:

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника.

Формулы площади круга

Формула площади круга через радиус

Площадь круга равна произведению квадрата радиуса на число пи.

S = π r 2 ,

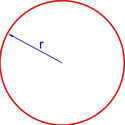
где S — площадь круга,
r — радиус круга.

Формула площади круга через диаметр

Площадь круга равна четверти произведения квадрата диаметра на число пи.

где S — площадь круга,
d — диаметр круга.

Площадь сегмента круга

Площадь кругового сегмента через угол в градусах.

где S — площадь сегмента круга,
R — радиус круга,
α° — угол в градусах.

Площадь кругового сегмента через угол в радианах.

где S — площадь сегмента круга,
R — радиус круга,
α° — угол в радианах.

Формула площади эллипса

Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.

где S — площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.

Площадь параллелограмма

Площадь параллелограмма, формулы и калькулятор для вычисления площади в режиме онлайн.

Для вычисления площади параллелограмма применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор для вычисления площади в режиме онлайн.

Площадь параллелограмма – это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.

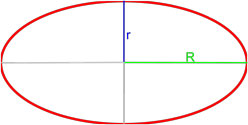
Площадь параллелограмма по основанию и высоте параллелограмма

Площадь параллелограмма по стороне и высоте, опущенной на эту сторону

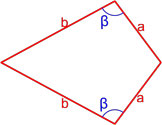
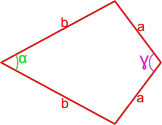
Площадь параллелограмма по двум сторонам и углу между ними

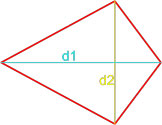
Площадь параллелограмма по двум диагоналям и углу между этими диагоналями

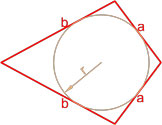
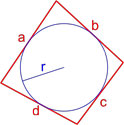
Площадь параллелограмма по вписанной окружности и стороне

Данная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб.

Площадь параллелограмма по вписанной окружности и углу между сторонами

Данная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб.

Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°

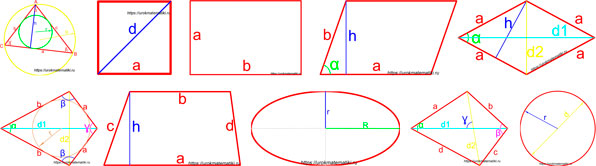
Таблица с формулами площади параллелограмма

исходные данные (активная ссылка для перехода к калькулятору)	эскиз	формула
1	основание и высота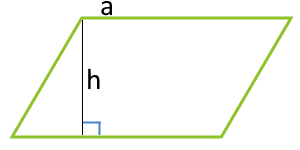
2	сторона и высота, опущенная на эту сторону
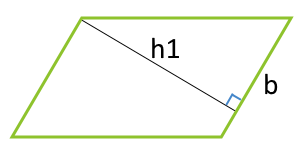3	две стороны и угол между ними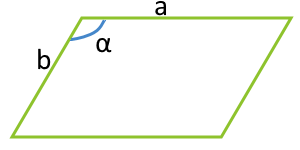
4	диагонали и угол между ними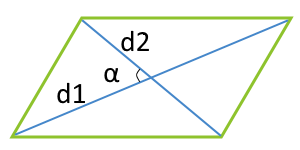
5	вписанная окружность и сторона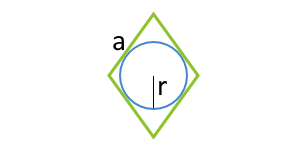
6	вписанная окружность и угол между сторонами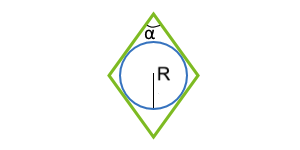

Определения

Параллелограмм — это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.

Высота параллелограмма – это отрезок проведенный из вершины параллелограмма к противоположной стороне под углом в 90 градусов.

Некоторые свойства параллелограмма:

• Сумма углов параллелограмма равна 360 градусов
• Сумма углов, прилегающих к любой из сторон равна 180 градусов
• Противоположные стороны параллельны и имеют одинаковую длину
• Противолежащие углы равны

Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.

Как найти площадь параллелограмма, треугольника, трапеции

Вы будете перенаправлены на Автор24

Площадь параллелограмма

Площадь параллелограмма определяется как произведение длины его стороны, на высоту, проведенную к ней.

Математически это можно записать следующим образом

где $a$ сторона параллелограмма, $h$ — высота, проведенная к этой стороне.

Доказательство.

Пусть нам дан параллелограмм $ABCD$, у которого $AD=BC=a$. Проведем высоты $DF$ и $AE$ (рис. 1).

Очевидно, что фигура $FDAE$ — прямоугольник.

[angle BAE=<90>^0-angle A, ] [angle CDF=angle D-<90>^0=<180>^0-angle A-<90>^0=<90>^0-angle A=angle BAE]

Следовательно, так как $CD=AB, DF=AE=h$, по $I$ признаку равенства треугольников $triangle BAE=triangle CDF$. Тогда

Значит по теореме о площади прямоугольника:

Теорема доказана.

Площадь параллелограмма определяется как произведение длины его смежных сторон, на синус угла между этими сторонами.

Математически это можно записать следующим образом

где $a, b$ стороны параллелограмма, $alpha $ — угол между ними.

Доказательство.

Пусть нам дан параллелограмм $ABCD$, у которого $BC=a, CD=b, angle C=alpha $. Проведем высоту $DF=h$ (рис. 2).

По определению синуса, получим

Значит, по теореме $1$:

Теорема доказана.

Площадь треугольника

Площадь треугольника определяется как половина произведения длины его стороны, на высоту, проведенную к ней.

Математически это можно записать следующим образом

где $a$ сторона треугольника, $h$ — высота, проведенная к этой стороне.

Доказательство.

Пусть нам дан треугольник $ABC$, у которого $AB=a$. Проведем высоту $CH=h$. Достроим его до параллелограмма $ABCD$ (рис. 3).

Очевидно, что по $I$ признаку равенства треугольников $triangle ACB=triangle CDB$. Тогда

Значит по теореме $1$:

Теорема доказана.

Готовые работы на аналогичную тему

Площадь треугольника определяется как половина произведения длины его смежных сторон, на синус угла между этими сторонами.

Математически это можно записать следующим образом

где $a, b$ стороны треугольника, $alpha $ — угол между ними.

Доказательство.

Пусть нам дан треугольник $ABC$, у которого $AB=a$. Проведем высоту $CH=h$. Достроим его до параллелограмма $ABCD$ (рис. 3).

Очевидно, что по $I$ признаку равенства треугольников $triangle ACB=triangle CDB$. Тогда

Значит по теореме $1$:

Теорема доказана.

Площадь трапеции

Площадь трапеции определяется как половина произведения суммы длин его оснований, на его высоту.

Математически это можно записать следующим образом

Доказательство.

Пусть нам дана трапеция $ABCK$, где $AK=a, BC=b$. Проведем в ней высоты $BM=h$ и $KP=h$, а также диагональ $BK$ (рис. 4).

По теореме $3$, получим

Теорема доказана.

Пример задачи

Найти площадь равностороннего треугольника, если длина его стороны равняется $a.$

Решение.

Так как треугольник равносторонний, то все его углы равняются $<60>^0$.

Тогда, по теореме $4$, имеем

Заметим, что результат этой задачи можно применять при нахождении площади любого равностороннего треугольника с данной стороной.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 19 05 2021

Вы открыли страницу вопроса Как найти площадь параллелограмма если известна площадь треугольника?. Он относится к категории
Геометрия. Уровень сложности вопроса – для учащихся 5 — 9 классов.
Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие
ответы по интересующей теме. Чтобы получить наиболее развернутый ответ,
можно просмотреть другие, похожие вопросы в категории Геометрия,
воспользовавшись поисковой системой, или ознакомиться с ответами других
пользователей. Для расширения границ поиска создайте новый вопрос, используя
ключевые слова. Введите его в строку, нажав кнопку вверху.