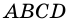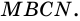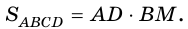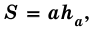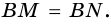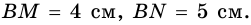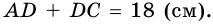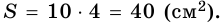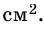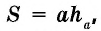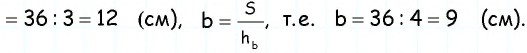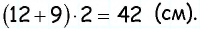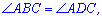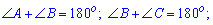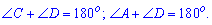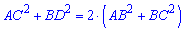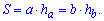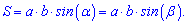Параллелограмм — это четырехугольник, в котором противоположные стороны равны и параллельны.
Онлайн-калькулятор площади параллелограмма
Параллелограмм обладает некоторыми полезными свойствами, которые упрощают решение задач, связанных с этой фигурой. Например, одно из свойств заключается в том, что противоположные углы параллелограмма равны.
Рассмотрим несколько способов и формул с последующим решением простых примеров.
Формула площади параллелограмма по основанию и высоте
Данный способ нахождения площади является, наверно, одним из основных и простых, так как он практически идентичен формуле по нахождению площади треугольника за небольшим исключением. Для начала разберем обобщенный случай без использования чисел.
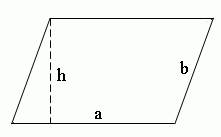
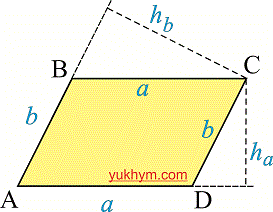
Пусть дан произвольный параллелограмм с основанием aa, боковой стороной bb и высотой hh, проведенной к нашему основанию. Тогда формула для площади этого параллелограмма:
S=a⋅hS=acdot h
aa — основание;
hh — высота.
Разберем одну легкую задачу, чтобы потренироваться в решении типовых задач.
Найти площадь параллелограмма, в котором известно основание, равное 10 (см.) и высота, равная 5 (см.).
Решение
a=10a=10
h=5h=5
Подставляем в нашу формулу. Получаем:
S=10⋅5=50S=10cdot 5=50 (см. кв.)
Ответ: 50 (см. кв)
Формула площади параллелограмма по двум сторонам и углу между ними
В этом случае искомая величина находится так:
S=a⋅b⋅sin(α)S=acdot bcdotsin(alpha)
a,ba, b — стороны параллелограмма;
αalpha — угол между сторонами aa и bb.
Теперь решим другой пример и воспользуемся вышеописанной формулой.
Найти площадь параллелограмма если известна сторона aa, являющаяся основанием и с длиной 20 (см.) и периметр pp, численно равный 100 (см.), угол между смежными сторонами (aa и bb) равен 30 градусам.
Решение
a=20a=20
p=100p=100
α=30∘alpha=30^{circ}
Для нахождения ответа нам неизвестна лишь вторая сторона данного четырехугольника. Найдем ее. Периметр параллелограмма дается формулой:
p=a+a+b+bp=a+a+b+b
100=20+20+b+b100=20+20+b+b
100=40+2b100=40+2b
60=2b60=2b
b=30b=30
Самое сложное позади, осталось только подставить наши значения для сторон и угла между ними:
S=20⋅30⋅sin(30∘)=300S=20cdot 30cdotsin(30^{circ})=300 (см. кв.)
Ответ: 300 (см. кв.)
Формула площади параллелограмма по диагоналям и углу между ними
S=12⋅D⋅d⋅sin(α)S=frac{1}{2}cdot Dcdot dcdotsin(alpha)
DD — большая диагональ;
dd — малая диагональ;
αalpha — острый угол между диагоналями.
Даны диагонали параллелограмма, равные 10 (см.) и 5 (см.). Угол между ними 30 градусов. Вычислить его площадь.
Решение
D=10D=10
d=5d=5
α=30∘alpha=30^{circ}
S=12⋅10⋅5⋅sin(30∘)=12.5S=frac{1}{2}cdot 10 cdot 5 cdotsin(30^{circ})=12.5 (см. кв.)
Ответ: 12.5 (см. кв.)
Решение контрольной работы по геометрии онлайн — от профильных экспертов Студворк!
Тест по теме «Площадь параллелограмма»
Преподаватель который помогает студентам и школьникам в учёбе.
Площадь параллелограмма — определение и вычисление с примерами решения
Теорема (о площади параллелограмма). Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне.
Доказательство:
Пусть 
1) Проведем высоту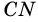 
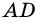
к прямой, содержащей сторону 
параллелограмма.
2) 
(как соответственные углы при параллельных прямых 
и 
и секущей 
Поэтому 
(по гипотенузе и острому углу).
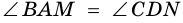
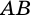
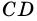
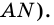
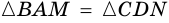
3) Параллелограмм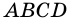 
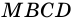
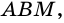
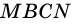
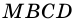
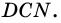
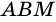
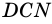
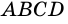
состоит из трапеции 
и треугольника 
а прямоугольник 
— из трапеции 
и треугольника 
Так как треугольники 
и 
равны, то равны и их площади, а потому равными будут площади параллелограмма 
и прямоугольника 
4) 
Но 
и поэтому 
Следовательно, 
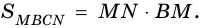
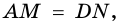
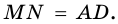
Заметим, что если основание высоты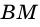 
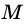
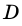
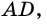
— точка 
-совпадает с точкой 
или лежит на продолжении стороны 
то доказательство теоремы будет аналогичным.
В общем виде формулу площади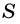 
параллелограмма можно записать так:
где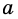 
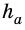
— сторона параллелограмма, 
— высота, к ней проведенная.
Пример:
Докажите, что высоты ромба, проведенные из одной вершины, равны.
Доказательство:
Пусть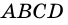 
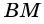
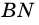
— данный ромб, 
и 
— его высоты (рис. 232).
Ромб является параллелограммом, поэтому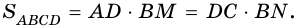 
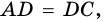
Но 
а значит 
Пример:
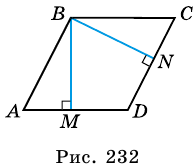
Периметр параллелограмма равен 36 см, а его высоты — 4 см и 5 см. Найдите площадь параллелограмма.
Решение:
1) Пусть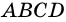 
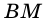
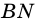
— данный параллелограмм, 
и 
— его высоты (рис. 232), 
2) 
По условию 
поэтому 
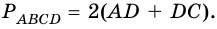
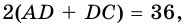
3) Пусть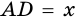 
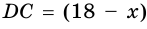
см, тогда 
см.
4) Так как по формуле площади параллелограмма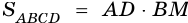 
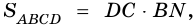
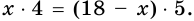
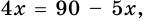
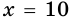
или 
имеем уравнение: 
То есть 
откуда 
(см).
5) Тогда 
Ответ. 40 
Площадь параллелограмма
С помощью формулы площади прямоугольника можно доказать формулу площади произвольного параллелограмма.
Теорема (формула площади параллелограмма)
Площадь параллелограмма равна произведению его стороны на высоту, проведенную к этой стороне:
где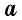 
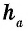
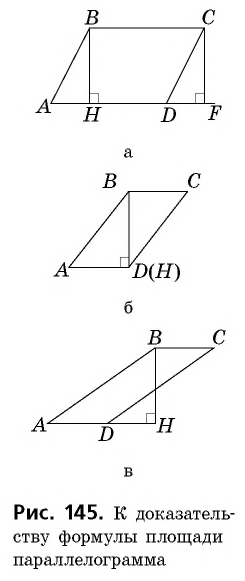
— сторона параллелограмма, 
— проведенная к ней высота.
Доказательство:
Пусть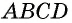 
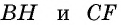
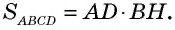
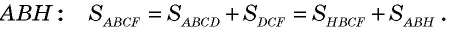
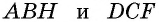
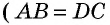
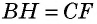
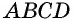
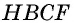
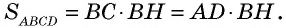
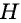
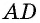
— данный параллелограмм, не являющийся прямоугольником (рис. 145, а). Проведем его высоты 
и докажем, что 
Четырехугольник 
является прямоугольной трапецией, площадь которой можно вычислить двумя способами — как сумму площадей параллелограмма 
и треугольника 
или как сумму площадей прямоугольника 
и треугольника 
Треугольники 
равны по гипотенузе и катету 
как противолежащие стороны параллелограмма, 
как расстояния между параллельными прямыми). Следовательно, эти треугольники имеют равные площади. Тогда площади параллелограмма 
и прямоугольника 
также равны, т.е. 
Случаи, когда точка 
не является внутренней точкой отрезка 
(рис. 145, б, в), рассмотрите самостоятельно.
Пример:
Площадь параллелограмма равна 
а длины его высот — 3 см и 4 см. Найдите периметр параллелограмма.
Решение:
Пусть дан параллелограмм с площадью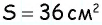 
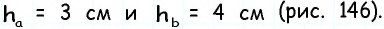
и высотами 
(рис. 146).
Поскольку 
Следовательно, периметр параллелограмма равен 
Ответ: 42 см.
Решая приведенную задачу, можно заметить интересную закономерность: чем больше сторона параллелограмма, тем меньше проведенная к ней высота.
- Прямоугольник и его свойства
- Ромб и его свойства, определение и примеры
- Квадрат и его свойства
- Трапеция и ее свойства
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Четырехугольники и окружность
- Параллелограмм, его свойства и признаки
Содержание:
- Формула площади параллелограмма:
- Формула периметра параллелограмма:
Параллелограмм — это четырёхугольник, у которого противолежащие
стороны попарно параллельны, т.е. лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник,
квадрат и ромб.
Формула площади параллелограмма:
Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры.
Величина площади параллелограмма выражается числом заключающихся в него квадратных единиц.
1) Площадь параллелограмма равна произведению длины его основания на длину высоты (a, h).
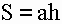
S — площадь параллелограмма
a — длина основания
h — длина высоты
См. также: Программа для расчета площади параллелограмма.
Формула периметра параллелограмма:
Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры.
Периметр имеет ту же размерность величин, что и длина.
1) Периметр параллелограмма равен удвоенной сумме 2-х его смежных сторон (a, b).
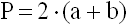
P — периметр параллелограмма
a — длина 1-ой стороны параллелограмма
b — длина 2-ой стороны параллелограмма
См. также: Программа для расчета периметра параллелограмма.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
А) Пусть одна сторона параллелограмма — a; другая — b. Так как площадь параллелограмма равна произведению стороны на высоту проведенную к этой стороне, то площадь параллелограмма S = a•6 или S = b•8
Получаем 6a = 8b или b = 3a/4
Периметр параллелограмма равен 2a + 2b = 42. Подставляем b.
Получаем 2а + 3а/2 = 42
а = 42•2/7 = 12 см
S = 12•6 = 72 см²
Ответ: S = 72 см²
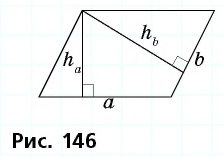
Б) Проведя высоту имеем прямоугольный треугольник с гипотенузой = 5, катетом = 4 (катет меньше гипотенузы) и катетом = h. По теореме Пифагора h = √(25-16) = 3 см
И площадь равна произведению стороны на высоту к данной стороне
S = 3•(4+6) = 30 см²
Ответ: S = 30 см²
В) Тут надо знать формулу, что площадь параллелограмма равна произведению сторон на синус угла между ними.
S = 8•10•sin30˚ = 80•1/2 = 40 см²
Ответ: S = 40 см²
Параллелограммом называют четырехугольник у которого противоположные стороны параллельны между собой. Основные задачи в школе по данной теме заключаются в вычислении площади параллелограмма, его периметра, высоты, диагоналей. Указанные величины и формулы для их вычисления будут приведены ниже.
Свойства параллелограмма
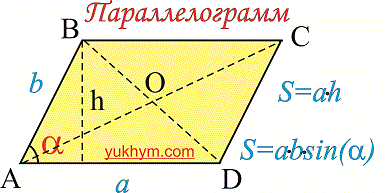
Противоположные стороны параллелограмма как и противоположные углы равны между собой:
AB=CD, BC=AD,
Диагонали параллелограмма в точке пересечения делятся на две равные части:
АО=OC, OB=OD.
Углы прилегающие к любой стороне (соседние углы) в сумме равны 180 градусов.
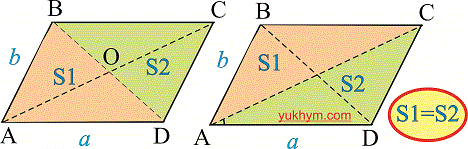
Каждая из диагоналей параллелограмма делит его на два одинаковые по площади и геометрическими размерами треугольники.
Еще одно замечательное свойство которое часто применяют при решении задач состоит в том, что сумма квадратов диагоналей в параллелограмме равна сумме квадратов всех сторон:
AC^2+BD^2=2*(AB^2+BC^2).
Основные признаки параллелограммов:
1. Четырехугольник у которого противоположные стороны попарно параллельны является параллелограммом.
2. Четырехугольник с равными противоположными сторонами является параллелограммом.
3. Четырехугольник с равными и параллельными противоположными сторонами является параллелограммом.
4. Если диагонали четырехугольника в точке пересечения делятся пополам то это параллелограмм.
5. Четырехугольник у которого противоположные углы попарно равны является параллелограммом
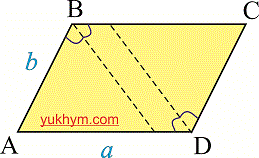
Биссектрисы параллелограмма
Биссектрисы противоположных углов в параллелограмме могут быть параллельными или совпадать.
Биссектрисы соседних углов ( прилегающие к одной стороне ) пересекаются под прямым углом (перпендикулярные).
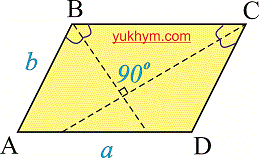
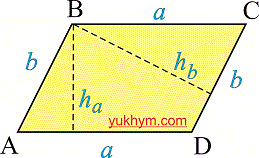
Высота параллелограмма
Высота параллелограмма — это отрезок который проведен с угла перпендикулярно к основанию. Из этого следует что из каждого угла можно провести две высоты.
Формула площади параллелограмма
Площадь параллелограмма равна произведению стороны на высоту проведенную к ней. Формула площади следующая
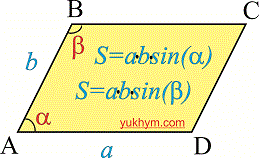
Вторая формула не менее популярная при вычислениях и определяется так: площадь параллелограмма равна произведению соседних сторон на синус угла между ними
На основе приведенных формул Вы будете знать как вычислить площадь параллелограмма.
Периметр параллелограмма
Формула для вычисления периметру параллелограмма имеет вид
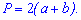
то есть периметр равен удвоенному значению суммы сторон. Задачи на параллелограмм будут рассмотрены в соседних материалах, а пока изучайте формулы. Большинство задач по вычислению сторон, диагоналей параллелограмма достаточно просты и сводятся к знанию теоремы синусов и теоремы Пифагора.
Посмотреть материалы:
- Прямоугольный треугольник. Задачи
- Площадь треугольника. Формулы
- Периметр и площадь прямоугольника
- Квадрат. Формулы
- Формулы площади трапеции
- Ромб. Площадь, периметр