Как найти площадь параллелограмма вписанного в четырехугольник - Исправление недочетов и поиск решений вместе с Examum.ru

Площадь четырехугольника

Площадь произвольного четырехугольника, формулы и калькулятор для вычисления в режиме онлайн. Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь произвольного четырехугольника или проверить уже выполненные вычисления.

В окончании статьи приведены ссылки для вычисления частных случаев четырехугольников: квадрата, трапеции, параллелограмма, прямоугольника, ромба.

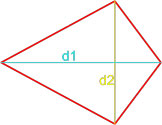
Площадь четырехугольника по диагоналям и углу между ними

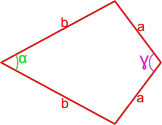
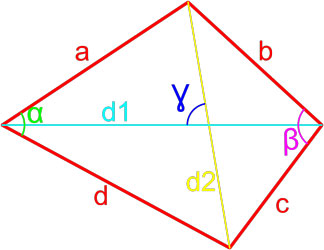
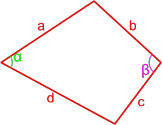
Площадь четырехугольника через стороны и углы между этими сторонами

При вычислении площади четырехугольника с использованием данной формулы, необходимо предварительно вычислить полупериметр четырехугольника по формуле:

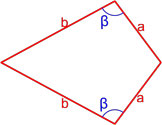
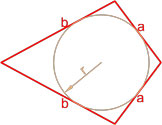
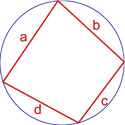
Площадь четырехугольника вписанного в окружность, вычисляемая по Формуле Брахмагупты

Данная формула справедлива только для четырехугольников, вокруг которых можно описать окружность.

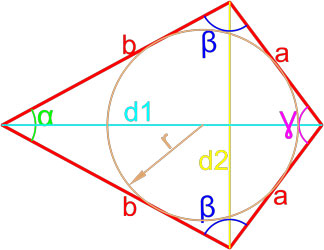
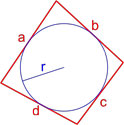
Площадь четырехугольника в который можно вписать окружность

Данная формула справедлива только для четырехугольников, в которые можно вписать окружность. Вписанная окружность должна иметь точки соприкосновения со всеми четырьмя сторонами четырехугольника.

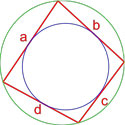
Площадь четырехугольника в который можно вписать окружность, определяемая через стороны и углы между ними

Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°

Таблица с формулами площади четырехугольника

исходные данные (активная ссылка для перехода к калькулятору)	эскиз	формула
1	диагональ и угол между ними
2	стороны и углы между этими сторонами
3	стороны (по Формуле Брахмагупты)
4	стороны и радиус вписанной окружности
5	стороны и углы между ними

Площадь частных случаев четырехугольников

Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:

Определения

Четырехугольник – это геометрическая плоская фигура, образованная четырьмя последовательно соединенными отрезками.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь четырехугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.

Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.

Формулы площадей фигур

Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.

Формулы площади треугольника

Формула площади треугольника по стороне и высоте

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты.

где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.

Формула площади треугольника по трем сторонам

Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c .

S = p p — a p — b p — c ,

где p — полупериметр треугольника: p = a + b + c 2
a, b, c — стороны треугольника.

Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

S = 1 2 a · b · sin γ ,

где a, b — стороны треугольника,
γ — угол между сторонами a и b .

Формула площади треугольника по трем сторонам и радиусу описанной окружности

a, b, c — стороны треугольника,
R — радиус описанной окружности.

Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c 2

Формулы площади квадрата

Формула площади квадрата по длине стороны

Площадь квадрата равна квадрату длины его стороны.

где S — площадь квадрата,
a — длина стороны квадрата.

Формула площади квадрата по длине диагонали

Площадь квадрата равна половине квадрата длины его диагонали.

где S — площадь квадрата,
d — длина диагонали квадрата.

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон.

где S — площадь прямоугольника,
a, b — длины сторон прямоугольника.

Формулы площади параллелограмма

Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.

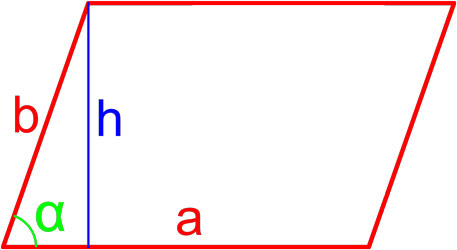
Формула площади параллелограмма по длине стороны и высоте

Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

где S — площадь параллелограмма,
a, h — длины сторон параллелограмма.

Формула площади параллелограмма по двум сторонам и углу между ними

Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

где S — площадь параллелограмма,
a, b — длины сторон параллелограмма,
α — угол между сторонами параллелограмма.

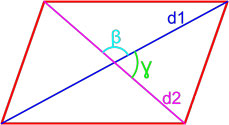
Формула площади параллелограмма по двум диагоналям и углу между ними

Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.

S = d1 · d2 · sin β 2 = d1 · d2 · sin γ 2 ,

где S — площадь параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
β , γ — угол между диагоналями параллелограмма.

Формулы площади ромба

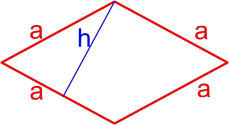
Формула площади ромба по длине стороны и высоте

Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

где S — площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба.

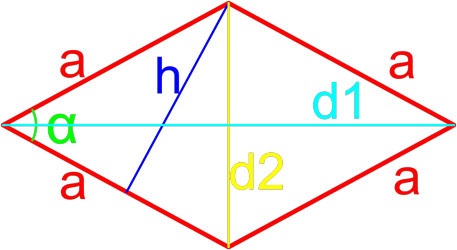
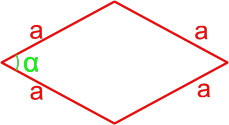
Формула площади ромба по длине стороны и углу

Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

где S — площадь ромба,
a — длина стороны ромба,
α — угол между сторонами ромба.

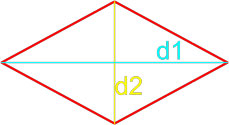
Формула площади ромба по длинам его диагоналей

Площадь ромба равна половине произведению длин его диагоналей.

где S — площадь ромба,
d1, d2 — длины диагоналей ромба.

Формулы площади трапеции

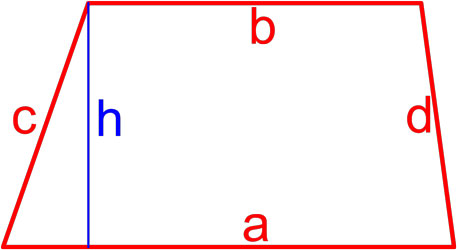
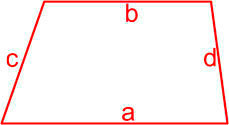
Трапеция — это четырёхугольник, у которого две ( a, b ) стороны параллельны (основания), а две другие ( c, d ) стороны не параллельны (боковые стороны).

Формула Герона для трапеции

где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p = a + b + c + d 2 — полупериметр трапеции.

Формула площади трапеции по длине основ и высоте

Площадь трапеции равна произведению полусуммы её оснований на высоту.

где S — площадь трапеции,
a, b — длины основ трапеции,
h — высота трапеции.

Формулы площади дельтоида

Дельтоид — это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания.

Формула площади дельтоида по двум неравным сторонам и углу между ними

Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.

где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
β — угол между неравными сторонами дельтоида.

Формула площади дельтоида по равным сторонам и углу между ними

Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.

S = a 2 sin γ + b 2 sin α 2 ,

где S — площадь дельтоида,
a, b — длины сторон дельтоида,
α — угол между равными сторонами b ,
γ — угол между равными сторонами a .

Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности

Площадь дельтоида равна произведению суммы неравных сторон на радиус вписанной окружности.

где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
r — радиус вписанной окружности.

Формула площади дельтоида по двум диагоналям

Площадь дельтоида равна половине произведения длин двух диагоналей.

где S — площадь дельтоида,
d1, d2 — диагонали дельтоида.

Формулы площади произвольного выпуклого четырехугольника

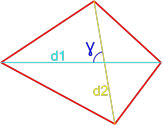
Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними

Площадь произвольного выпуклого выпуклого четырехугольника равна половине произведения его диагоналей умноженной на синус угла между ними.

S = d1 · d2 · sin γ 2 ,

где S — площадь четырехугольника,
d1, d2 — диагонали четырехугольника,
γ — любой из четырёх углов между диагоналями.

Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника,
θ = α + β 2 — полусумма двух противоположных углов четырехугольника.

Формула площади вписанного четырехугольника (формула Брахмагупты)

Если вокруг четырехугольника можно описать окружность, то его площадь равна

S = p — a p — b p — c p — d ,

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p = a + b + c + d 2 — полупериметр четырехугольника.

Формула площади четырехугольника с вписанной окружностью

Если в четырехугольник можно вписать окружность, то его площадь равна:

где S — площадь четырехугольника,
r — радиус вписанной окружности,
p = a + b + c + d 2 — полупериметр четырехугольника.

Формула площади четырехугольника с вписанной и описанной окружностями

Если в четырехугольник можно вписать окружность, а также около него можно описать окружность, то его площадь равна:

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника.

Формулы площади круга

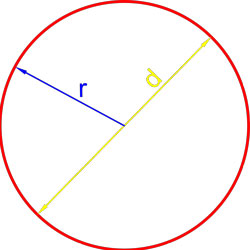
Формула площади круга через радиус

Площадь круга равна произведению квадрата радиуса на число пи.

S = π r 2 ,

где S — площадь круга,
r — радиус круга.

Формула площади круга через диаметр

Площадь круга равна четверти произведения квадрата диаметра на число пи.

где S — площадь круга,
d — диаметр круга.

Площадь сегмента круга

Площадь кругового сегмента через угол в градусах.

где S — площадь сегмента круга,
R — радиус круга,
α° — угол в градусах.

Площадь кругового сегмента через угол в радианах.

где S — площадь сегмента круга,
R — радиус круга,
α° — угол в радианах.

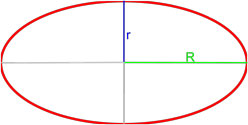
Формула площади эллипса

Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.

где S — площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.

Площади четырехугольников

Формулы для площадей четырехугольников

Вывод формул для площадей четырехугольников

Вывод формулы Брахмагупты для площади вписанного четырехугольника

В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:

которая позволяет найти площадь прямоугольника прямоугольника с основанием a и высотой b.

Формулы для площадей четырехугольников

a и b – смежные стороны

d – диагональ,
φ – любой из четырёх углов между диагоналями

Получается из верхней формулы подстановкой d=2R

R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

a – сторона,
h_a – высота, опущенная на эту сторону

a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

a – сторона квадрата

Получается из верхней формулы подстановкой d = 2R

a – сторона,
h_a – высота, опущенная на эту сторону

a – сторона,
φ – любой из четырёх углов ромба

r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

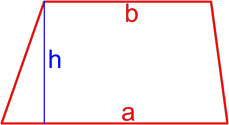
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

a и b – основания,
c и d – боковые стороны

a и b – неравные стороны,
φ – угол между ними

a и b – неравные стороны,
φ₁ – угол между сторонами, равными a ,
φ₂ – угол между сторонами, равными b .

a и b – неравные стороны,
r – радиус вписанной окружности

φ – любой из четырёх углов между ними

a, b, c, d – длины сторон четырёхугольника,
p – полупериметр,

Формулу называют «Формула Брахмагупты»

Четырехугольник	Рисунок	Формула площади	Обозначения
Прямоугольник		S = ab


Параллелограмм


Квадрат		S = a 2
	S = 4r 2


Ромб




Трапеция
	S = m h


Дельтоид		S = ab sin φ



Произвольный выпуклый четырёхугольник
Вписанный четырёхугольник

где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

Формула получается из верхней формулы подстановкой d = 2R

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Получается из верхней формулы подстановкой d = 2R

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба

где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

где
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
r – радиус вписанной окружности

φ – любой из четырёх углов между ними

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр

Формулу называют «Формула Брахмагупты»

Прямоугольник



Параллелограмм



Квадрат
	S = a 2 где a – сторона квадрата
	S = 4r 2


Ромб





Трапеция




Дельтоид

	где a и b – неравные стороны, φ₁ – угол между сторонами, равными a , φ₂ – угол между сторонами, равными b .


Произвольный выпуклый четырёхугольник

Вписанный четырёхугольник

где
a и b – смежные стороны

где
d – диагональ,
φ – любой из четырёх углов между диагоналями

где
R – радиус описанной окружности,
φ – любой из четырёх углов между диагоналями

Формула получается из верхней формулы подстановкой d = 2R

Параллелограмм

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a и b – смежные стороны,
φ – угол между ними

φ – любой из четырёх углов между ними

Квадрат

где
a – сторона квадрата

Получается из верхней формулы подстановкой d = 2R

Ромб

где
a – сторона,
h_a – высота, опущенная на эту сторону

где
a – сторона,
φ – любой из четырёх углов ромба

где
r – радиус вписанной окружности,
φ – любой из четырёх углов ромба

Трапеция

где
a и b – основания,
h – высота

φ – любой из четырёх углов между ними

где
a и b – основания,
c и d – боковые стороны ,

Дельтоид

где
a и b – неравные стороны,
φ – угол между ними

где
a и b – неравные стороны,
φ₁ – угол между сторонами, равными a ,
φ₂ – угол между сторонами, равными b .

где
a и b – неравные стороны,
r – радиус вписанной окружности

Произвольный выпуклый четырёхугольник

φ – любой из четырёх углов между ними

Вписанный четырёхугольник

где
a, b, c, d – длины сторон четырёхугольника,
p – полупериметр

Формулу называют «Формула Брахмагупты»

Вывод формул для площадей четырехугольников

Утверждение 1 . Площадь выпуклого четырёхугольника можно найти по формуле

Доказательство . В соответствии с рисунком 1 справедливо равенство:

что и требовалось доказать.

Утверждение 2 . Площадь параллелограмма параллелограмма можно найти по формуле

где a – сторона параллелограмма, а h_a – высота высота высота , опущенная на эту сторону (рис. 2).

Доказательство . Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому

что и требовалось доказать.

Утверждение 3 .Площадь параллелограмма параллелограмма можно найти по формуле

где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).

то, в силу утверждения 2, справедлива формула

что и требовалось доказать.

Утверждение 4 . Площадь ромба ромба можно найти по формуле

где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).

что и требовалось доказать.

Утверждение 5 . Площадь трапеции можно найти по формуле

где a и b – основания трапеции, а h – высота высота высота (рис.5).

Доказательство . Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD . Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF . Поэтому

что и требовалось доказать.

Утверждение 6 . Площадь трапеции трапеции можно найти по формуле

где a и b – основания, а c и d – боковые стороны трапеции ,

(рис.6).

Доказательство . Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):

что и требовалось доказать.

Утверждение 7 . Площадь дельтоида, дельтоида, можно найти по формуле:

где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).

Доказательство . Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D , а биссектрисы углов A и C пересекаются в некоторой точке O , лежащей на диагонали BD . Точка O и является центром вписанной в дельтоид окружности.

Если r – радиус вписанной в дельтоид окружности, то

источники:

http://urokmatematiki.ru/reference-information/formuly-po-geometrii/formuly-ploshchadey-figur.php

http://www.resolventa.ru/spr/planimetry/sqf.htm

Источник

Как найти площадь вписанного четырехугольника?

I способ.

Площадь вписанного четырёхугольника может быть найдена по формуле Брахмагупты:

где p — полупериметр четырёхугольника, то есть

$[p = frac{{a + b + c + d}}{2}.]$

(формулу Герона можно рассматривать как частный случай этой формулы при d=0).

II способ.

Площадь четырёхугольника ABCD, вписанного в окружность, можно найти как сумму площадей треугольников, например, ABC и ADC.

Из треугольника ABC по теореме косинусов

$[A{C^2} = A{B^2} + B{C^2} - 2 cdot AB cdot BC cdot cos angle ABC.]$

Аналогично, из треугольника ADC

$[A{C^2} = A{D^2} + D{C^2} - 2 cdot AD cdot DC cdot cos angle ADC.]$

Так как четырехугольник ABCD вписан в окружность,

$[angle ABC + angle ADC = {180^o}]$

Так как cos(180º-α)= — cosα

$[cos angle ADC = cos ({180^o} - angle ABC) = - cos angle ADC]$

Отсюда,

$[A{C^2} = A{D^2} + D{C^2} + 2 cdot AD cdot DC cdot cos angle ABC.]$

Приравниваем правы части равенств для AC²

$[A{D^2} + D{C^2} + 2 cdot AD cdot DC cdot cos angle ABC = ]$

$[ = A{B^2} + B{C^2} - 2 cdot AB cdot BC cdot cos angle ABC.]$

Отсюда,

$[ - A{B^2} + B{C^2} - A{D^2} - D{C^2},]$

$[ = A{B^2} + B{C^2} - A{D^2} - D{C^2}]$

$[cos angle ABC = frac{{A{B^2} + B{C^2} - A{D^2} - D{C^2}}}{{2(AB cdot BC + AD cdot DC)}}.]$

Найдём синус этого угла, используя основное тригонометрическое тождество

$[{sin ^2}alpha + {cos ^2}alpha = 1]$

(для 0º<α<180º sinα>0)

$[sin angle ABC = sqrt {1 - {{(cos angle ABC)}^2}} ]$

и по формуле

$[S = frac{1}{2}a cdot b cdot sin alpha ]$

найдём

$[{S_{Delta ABC}} = frac{1}{2} cdot AB cdot BC cdot sin angle ABC.]$

Аналогично,

$[{S_{Delta ADC}} = frac{1}{2} cdot AD cdot DC cdot sin angle ADC,]$

(так как их сумма равна 180º, а sin(180º-α )=sinα).

$[{S_{ABCD}} = {S_{Delta ABC}} + {S_{Delta ADC}}.]$

В частных случаях: если в окружность вписан правильный четырёхугольник (то есть квадрат), прямоугольник либо четырёхугольник, диагонали которого взаимно перпендикулярны — решение задачи может быть упрощено.

Площадь любого четырёхугольника, в том числе, и вписанного, равна половине произведения его диагоналей на синус угла между ними:

$[S = frac{1}{2}{d_1} cdot {d_2} cdot sin varphi ]$

В следующий раз рассмотрим конкретные примеры нахождения площади вписанного четырёхугольника.

Источник

Формулы площадей фигур

формулы площади треугольника
формулы площади квадрата
формула площади прямоугольника
формулы площади параллелограмма
формулы площади ромба
формулы площади трапеции
формулы площади дельтоида
формулы площади произвольного выпуклого четырехугольника
формулы площади круга
формула площади эллипса

Формулы площади треугольника

Формула площади треугольника по стороне и высоте

S = 12 a · h

где a — одна из сторон треугольника, h — высота, проведенная к стороне треугольника.

Формула площади треугольника по трем сторонам

Формула Герона формула для вычисления площади треугольника S по длинам его сторон a, b, c.

S = pp-ap-bp-c

где p — полупериметр треугольника: p = a + b + c2
a, b, c — стороны треугольника.

Формула площади треугольника по двум сторонам и углу между ними

Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.

S = 12 a · b · sinγ

где a, b — стороны треугольника,
γ — угол между сторонами a и b.

Формула площади треугольника по трем сторонам и радиусу описанной окружности

S = a · b · c4R

a, b, c — стороны треугольника,
R — радиус описанной окружности.

Формула площади треугольника по трем сторонам и радиусу вписанной окружности

Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.

S = p · r

где S — площадь треугольника,
r — радиус вписанной окружности,
p — полупериметр треугольника: p = a + b + c2

Формулы площади квадрата

Формула площади квадрата по длине стороны

Площадь квадрата равна квадрату длины его стороны.

S = a2

где S — площадь квадрата,
a — длина стороны квадрата.

Формула площади квадрата по длине диагонали

Площадь квадрата равна половине квадрата длины его диагонали.

S = d22

где S — площадь квадрата,
d — длина диагонали квадрата.

Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон.

S = a · b

где S — площадь прямоугольника,
a, b — длины сторон прямоугольника.

Формулы площади параллелограмма

Параллелограмм — это четырёхугольник, у которого противолежащие стороны параллельны.

Формула площади параллелограмма по длине стороны и высоте

Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.

S = a · h

где S — площадь параллелограмма,
a, h — длины сторон параллелограмма.

Формула площади параллелограмма по двум сторонам и углу между ними

Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.

S = a · b · sinα

Формула площади параллелограмма по двум диагоналям и углу между ними

S =
d1 · d2
· sinβ2 = d1 · d2
· sinγ2

где S — площадь параллелограмма,
d1, d2 — длины диагоналей параллелограмма,
β, γ — угол между диагоналями параллелограмма.

Формулы площади ромба

Формула площади ромба по длине стороны и высоте

Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

S = a · h

где S — площадь ромба,
a — длина стороны ромба,
h — длина высоты ромба.

Формула площади ромба по длине стороны и углу

Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

S = a2 · sinα

где S — площадь ромба,
a — длина стороны ромба,
α — угол между сторонами ромба.

Формула площади ромба по длинам его диагоналей

Площадь ромба равна половине произведению длин его диагоналей.

S = d1 · d22

где S — площадь ромба,
d1, d2 — длины диагоналей ромба.

Формулы площади трапеции

Трапеция — это четырёхугольник, у которого две (a, b) стороны параллельны (основания), а две другие (c, d) стороны не параллельны (боковые стороны).

Формула Герона для трапеции

S = a + b|a — b| p-ap-bp-a-cp-a-d

где S — площадь трапеции,
a, b — длины основ трапеции,
c, d — длины боковых сторон трапеции,
p=a+b+c+d2 — полупериметр трапеции.

Формула площади трапеции по длине основ и высоте

Площадь трапеции равна произведению полусуммы её оснований на высоту.

S = a + b · h2

где S — площадь трапеции,
a, b — длины основ трапеции,
h — высота трапеции.

Формулы площади дельтоида

Формула площади дельтоида по двум неравным сторонам и углу между ними

Площадь дельтоида равна произведению длин неравных сторон на синус угла между ними.

S = a·b sinβ

Формула площади дельтоида по равным сторонам и углу между ними

Площадь дельтоида равна полусумме произведения каждой из пар равных сторон на синус угла между ними.

S = a2 sinγ + b2 sinα2

где S — площадь дельтоида,
a, b — длины сторон дельтоида,
α — угол между равными сторонами b,
γ — угол между равными сторонами a.

Формула площади дельтоида по двум неравным сторонам и радиусу вписанной окружности

Площадь дельтоида равна произведению суммы неравных сторон на радиус вписанной окружности.

S = a+b r

где S — площадь дельтоида,
a, b — длины неравных сторон дельтоида,
r — радиус вписанной окружности.

Формула площади дельтоида по двум диагоналям

Площадь дельтоида равна половине произведения длин двух диагоналей.

S = d1 · d22

где S — площадь дельтоида,
d1, d2 — диагонали дельтоида.

Формулы площади произвольного выпуклого четырехугольника

Формула площади произвольного выпуклого четырехугольника по длине диагоналей и углу между ними

S = d1 · d2 · sinγ2

Формула площади произвольного выпуклого четырехугольника по длине сторон и значению противоположных углов

S = p-ap-bp-cp-d — a·b·c·d ·cos2θ

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p=a+b+c+d2 — полупериметр четырехугольника,
θ = α + β2 — полусумма двух противоположных углов четырехугольника.

Формула площади вписанного четырехугольника (формула Брахмагупты)

Если вокруг четырехугольника можно описать окружность, то его площадь равна

S = p-ap-bp-cp-d

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника,
p=a+b+c+d2 — полупериметр четырехугольника.

Формула площади четырехугольника с вписанной окружностью

Если в четырехугольник можно вписать окружность, то его площадь равна:

S = p· r

где S — площадь четырехугольника,
r — радиус вписанной окружности,
p=a+b+c+d2 — полупериметр четырехугольника.

Формула площади четырехугольника с вписанной и описанной окружностями

S = a·b·c·d

где S — площадь четырехугольника,
a, b, c, d — длины сторон четырехугольника.

Формулы площади круга

Формула площади круга через радиус

Площадь круга равна произведению квадрата радиуса на число пи.

S = πr2

где S — площадь круга,
r — радиус круга.

Формула площади круга через диаметр

Площадь круга равна четверти произведения квадрата диаметра на число пи.

S = πd24

где S — площадь круга,
d — диаметр круга.

Площадь сегмента круга

Площадь кругового сегмента через угол в градусах.

S = R22 · π · α°180° — sinα

где S — площадь сегмента круга,
R — радиус круга,
α° — угол в градусах.

Площадь кругового сегмента через угол в радианах.

S = R22 · αрад. — sinα

где S — площадь сегмента круга,
R — радиус круга,
α° — угол в радианах.

Формула площади эллипса

Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.

S = π · a · b

где S — площадь эллипса,
a — длина большей полуоси эллипса,
b — длина меньшей полуоси эллипса.

Коротко о важном
Таблицы
Формулы
Формулы по геометрии
Теория по математике

Источник

Вписанные и описанные четырехугольники

Вписанный четырехугольник — четырехугольник, все вершины которого лежат на одной окружности.
Очевидно, эта окружность будет называться описанной вокруг четырехугольника.

Описанный четырехугольник — такой, что все его стороны касаются одной окружности. В этом случае окружность вписана в четырехугольник.

Рассмотрим теоремы о вписанных и описанных четырехугольниках и их свойствах.

Теорема 1. Четырёхугольник можно вписать в окружность тогда и только тогда, когда суммы его противоположных углов равны $180^{circ }.$

$angle A +angle C = 180^{circ }$

Теорема 2. Четырёхугольник можно описать вокруг окружности тогда и только тогда, когда суммы его противоположных сторон равны.

a+c=b+d

Теорема 3. Диагонали вписанного четырёхугольника разбивают его на две пары подобных треугольников.

Теорема 4. (Птолемея). Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.

Теорема 5. Площадь описанного четырехугольника равна произведению полупериметра четырёхугольника на радиус вписанной в него окружности.

$displaystyle S=frac{a+b+c+d}{2}cdot r=pr$

Теорема 6. Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Теорема 7. Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Теорема 8. Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной.

Теорема 9. Биссектрисы всех внутренних углов описанного четырёхугольника пересекаются в одной точке – центре вписанной окружности.

Теорема 10. В любой ромб можно вписать окружность.

Теорема 11. В любой квадрат можно вписать окружность.

Теорема 12. В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом.

Теорема 13. В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.

Теорема 14. В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон равна сумме длин оснований.

c+d=a+b

Посмотрим, как эти свойства применяются в решении задач ЕГЭ.

Задача 1. Два угла вписанного в окружность четырехугольника равны $82^{circ}$ и $58^{circ}$ . Найдите больший из оставшихся углов. Ответ дайте в градусах.

Решение:

Сумма противоположных углов вписанного четырехугольника равна $180^{circ}$ . Пусть угол равен $82^{circ}$ . Тогда напротив него лежит угол в градусов. Если угол равен $58^{circ}$ , то угол равен $180^{circ}-58^{circ}=122^{circ}$ .

Ответ: 122.

Задача 2. Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 1:2:3 . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен .

Решение:

Пусть сторона равна , равна , а DC - 3x . По свойству описанного четырехугольника, суммы противоположных сторон равны, и значит,

Получается, что равна . Тогда периметр четырехугольника равен . Мы получаем, что x=4 , а большая сторона равна .

Ответ: 12.

Задача 3. Около окружности описана трапеция, периметр которой равен . Найдите ее среднюю линию.

Решение:

Мы помним, что средняя линия трапеции равна полусумме оснований. Пусть основания трапеции равны и , а боковые стороны — и . По свойству описанного четырехугольника,
a+c=b+d , и значит, периметр равен .
Получаем, что a+c=40 , а средняя линия равна .

Ответ: 10.

Задача 4. Угол A четырехугольника ABCD , вписанного в окружность, равен $32^{circ }$ . Найдите угол C этого четырехугольника. Ответ дайте в градусах.

Решение:

Четырехугольник ABCD вписан в окружность. Значит, сумма его противоположных углов равна $180^{circ }.$

Поэтому $angle C=180^{circ } -angle A=180^{circ }-32^{circ }=148^{circ }.$

Ответ: 148.

Задача 5. Углы A, B, C четырехугольника ABCD относятся как 1:2:3 . Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.

Решение:

Пусть

Сумма всех углов четырехугольника равна $360^{circ }.$

А сумма каждой пары противоположных углов равна $180^{circ }$ (т.к. четырехугольник вписан в окружность).

Запишем эти два условия в виде двух уравнений с двумя неизвестными:

Подставляем второе уравнение в первое и получаем $4x=180, x=45, y=90^{circ }.$

Ответ: 90.

Задача 6. Стороны четырехугольника ABCD и стягивают дуги описанной окружности, градусные величины которых равны соответственно $107^{circ }$ и $39^{circ }$ . Найдите угол C этого четырехугольника. Ответ дайте в градусах.

Решение:

Сумма противоположных углов вписанного четырехугольника равна $180^{circ }$ .

Поэтому $angle C=180^{circ } -angle A.$

Угол А – вписанный, опирается на дугу , равную сумме дуг и , т.е. $107^{circ }+39^{circ }=146^{circ }.$

Тогда вписанный угол А равен половине дуги , т.е. $146^{circ }:2=73^{circ }.$

$angle C=180^{circ } -angle A=180^{circ }-73^{circ }=107^{circ }.$

Ответ: 107.

Задача 7. Точки расположенные на окружности, делят эту окружность на четыре дуги и AD, градусные величины которых относятся соответственно как Найдите угол A четырехугольника ABCD. Ответ дайте в градусах.

Решение:

Угол А – вписанный, опирается на дугу BD, равную сумме дуг и CD. Найдем дуги и CD.

Обозначим градусные величины дуг и как согласно заданному соотношению между дугами.

Тогда или $36x=360, x=10^{circ }.$

Сумма дуг и составляет $x+2x=30^{circ }.$

Вписанный угол А равен половине дуги BD, т.е. $30^{circ }:2=15^{circ }.$

Ответ: 15.

Задача 8. Радиус окружности, описанной около квадрата, равен Найдите длину стороны этого квадрата.

Решение:

Радиус окружности, описанной около квадрата, равен половине диагонали квадрата. Тогда диагональ квадрата равна

Выразим сторону квадрата через его диагональ: $displaystyle a=frac{d}{sqrt{2}}=32.$

Ответ: 32.

Задача 9. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?

Решение:

Если правильный шестиугольник вписан в окружность, то радиус окружности равен стороне шестиугольника. Поэтому сторона равна 6.

Ответ: 6.

Задача 10. Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен $60^{circ }$ , большее основание равно 12. Найдите радиус описанной окружности этой трапеции.

Решение:

Поскольку трапеция вписана в окружность, она равнобедренная.

Рассмотрим равнобедренную трапецию ABCD с основаниями

Тогда боковые стороны

Проведем параллельно CD. Тогда треугольник ABO – равнобедренный, т.к. и равносторонний, т.к. $angle A = 60^{circ }.$ Поэтому AO=a.

BCDO – параллелограмм по построению, но BC=CD , поэтому BCDO – ромб, и OD=a.

Получаем, что О – центр описанной окружности с радиусом, равным меньшему основанию –

Ответ: 6.

Задача 11. Найти диагональ параллелограмма, вписанного в окружность радиусом 6 см.

Решение:

Согласно одной из теорем, окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Прямой угол, вписанный в окружность, опирается на диаметр. Поэтому диагональ равна диаметру, см.

Ответ: 12.

Задача 12. Около трапеции описана окружность. Периметр трапеции равен 60, средняя линия равна 25. Найдите боковую сторону трапеции.

Решение:

Средняя линия трапеции равна полусумме оснований. Поэтому сумма оснований

Сумму боковых сторон найдем как разность между периметром и суммой оснований:

Трапеция вписана в окружность, следовательно, трапеция равнобедренная, боковые стороны равны:

Ответ: 5.

Задача 13. Найдите радиус окружности, описанной около прямоугольника, две стороны которого равны 13 и

Решение:

Прямой угол, вписанный в окружность, опирается на диаметр. Поэтому диагональ равна диаметру окружности.

В то же время по теореме Пифагора диагональ найдем как

Радиус окружности равен половине диаметра: 18:2=9.

Ответ: 9.

Задача 14. Найдите радиус окружности, вписанной в квадрат со стороной 16.

Решение:

Радиус окружности, вписанной в квадрат, равен половине его стороны. Поэтому r = 8.

Ответ: 8.

Задача 15. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.

Решение:

Трапеция описана около окружности. Следовательно, сумма оснований равна сумме боковых сторон и равна 11 (половине периметра).

Боковая сторона CB = 7, тогда боковая сторона

Радиус вписанной окружности равен половине AD, т.е. 2.

Ответ: 2.

Задача 16. Найдите высоту трапеции, в которую вписана окружность радиуса 14.

Решение:

Высота трапеции, в которую вписана окружность, равна диаметру этой окружности:

Ответ: 28.

Задача 17. Боковые стороны трапеции, описанной около окружности, равны 19 и 13. Найдите среднюю линию трапеции.

Решение:

Трапеция описана около окружности. Следовательно, сумма оснований равна сумме боковых сторон и равна

Средняя линия трапеции равна полусумме оснований

Ответ: 16.

Задача 18. Около окружности, радиус которой равен 2, описан многоугольник, периметр которого равен 16. Найдите его площадь.

Решение:

Площадь описанного многоугольника можно найти как произведение полупериметра на радиус вписанной окружности:

Ответ: 16.

Задача 19. В равнобедренной трапеции, вписанной в окружность, диагонали взаимно перпендикулярны. Средняя линия трапеции равна 12. Найти радиус вписанной окружности.

Решение:

Радиус окружности, вписанной в трапецию, равен половине ее высоты.

Рассмотрим равнобедренную трапецию

Проведем Треугольник ACK – прямоугольный (с прямым углом С) и равнобедренный. Его гипотенуза равна сумме оснований трапеции (т.к. BCKD – параллелограмм, и BC = KD ),

Высота трапеции является также высотой и медианой, проведенной из прямого угла равнобедренного прямоугольного треугольника ACK .

Радиус вписанной окружности

Ответ: 6.

Задача 20. Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5. Центр окружности лежит внутри трапеции. Найдите высоту трапеции.

Решение:

Пусть О – центр описанной окружности. Проведем высоту MN, проходящую через точку О. Тогда (радиусы окружности),

Треугольники OMC и OND – прямоугольные. Применяя теорему Пифагора, найдем:

Ответ: 7.

Это были задачи по теме «Вписанные и описанные четырехугольники» из первой части ОГЭ и ЕГЭ. Покажем более сложную задачу, из второй части ОГЭ по математике.

Задача 21. В четырёхугольник ABCD можно вписать и вокруг него можно описать окружность. Диагонали этого четырёхугольника перпендикулярны. Найдите его площадь, если радиус описанной окружности равен 5, а AB=2BC.

Решение:

Обозначим BC=x. Тогда AB=2x.

Обозначим также

Вписать окружность в четырехугольник можно тогда и только тогда, когда суммы длин противоположных сторон четырехугольника равны.

Значит, Отсюда y=x+z.

Пусть О – точка пересечения диагоналей четырёхугольника ABCD.

При пересечении и образуется четыре прямоугольных треугольника. Это

Пусть

Запишем для каждого из этих треугольников теорему Пифагора:

Из $triangle AOB: 4x^{2}=a^{2}+b^{2}.$

Из $triangle BOC: x^{2}=b^{2}+c^{2}.$

Из $triangle COD: z^{2}=c^{2}+d^{2}.$

Из $triangle AOD: y^{2}=a^{2}+d^{2}.$

Мы получили систему уравнений.

Сложив первое и третье из них и выразив $x^{2}+y^{2}$ как $a^{2}+b^{2}+c^{2}+d^{2},$ получим: $4x^{2}+z^{2}=x^{2}+y^{2}.$

Кроме того, y=x+z. Это мы нашли в самом начале.

Из системы уравнений

$begin{cases}3x^{2}+z^{2}=y^{2} \y=x+zend{cases}$

находим:

Значит,

Перестроим чертеж. Это надо сделать обязательно. Появились новые данные – рисуем новый чертеж. По условию, четырехугольник ABCD вписан в окружность.

Треугольники ABC и ADC равны по трем сторонам. Значит, углы ABC и ADC равны.

Четырехугольник ABCD вписан в окружность, поэтому сумма углов ABC и ADC равна 180 градусов. Мы получили, что углы ABC и ADC – прямые. Тогда – диаметр окружности.

По условию, R=5 , тогда AC=10.

опирается на диаметр.

– прямоугольный, – его гипотенуза.

По теореме Пифагора для :

$100=x^{2}+4x^{2}.$

Отсюда $x^{2}=20.$

$S_{ABCD}=2cdot S_{triangle ABC}=2x^{2}=40.$

Ответ: 40.

Если вы хотите разобрать большее количество примеров — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Вписанные и описанные четырехугольники» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Параллелограмм – это геометрическая фигура; четырехугольник, у которого противоположные стороны равны и параллельны.

Формула вычисления площади
- По длине стороны и высоте
- По двум сторонам и углу между ними
- По двум диагоналям и углу между ними
Примеры задач

Формула вычисления площади

По длине стороны и высоте

Площадь параллелограмма (S) равняется произведению длины его стороны и высоты, проведенной к ней:

S = a ⋅ h

По двум сторонам и углу между ними

Площадь параллелограмма находится путем умножения длин его обеих сторон и синуса угла между ними:

S = a ⋅ b ⋅ sin α

По двум диагоналям и углу между ними

Площадь параллелограмма равна одной второй произведения длин его диагоналей, умноженного на синус угла между ними:

S = ¹/₂ ⋅ d₁ ⋅ d₂ ⋅ sin α

Примеры задач

Задание 1
Найдите площадь параллелограмма, если длина его стороны равняется 7 см, а высоты – 4 см.

Решение:
Используем первую формулу, в которой задействованы известные нам по условиям задания значения: S = 4 см * 7 см = 28 см².

Задание 2
Найдите площадь параллелограмма, если его стороны равны 6 и 8 см, а угол между ними – 30°.

Решение:
Применим вторую формулу, рассмотренную выше: S = 6 см * 8 см * sin 30° = 24 см².

Задание 3
Найдите площадь параллелограмма с диагоналями, равными 4 и 6 см. Угол между ними составляет 90°.

Решение:
Воспользуемся формулой, в которой фигурируют диагонали: S = 1/2 * 4 см * 6 см * sin 90° = 12 см².

Источник