Найдите площадь параллелограмма. Здравствуйте! В этой статье представлена группа заданий решение которых связанно с площадью параллелограмма. Задачи входят в состав экзамена. Рекомендую посмотреть статью в которой о площади параллелограмма (и треугольника) всё подробно расписано. При решении пригодятся формулы:
*Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними.
*Площадь параллелограмма равна произведению параллелограмма на высоту проведённую к этой стороне.
Также рассматриваются задачи с ромбами. Как известно, ромб является параллелограммом и обладает его свойствами, но есть ещё и дополнительные. Нам понадобится это:
— Диагонали ромба взаимно перпендикулярны.
Рассмотрим задачи:
27586. Найдите площадь ромба, если его стороны равны 1, а один из углов равен 1500.
Используем формулу площади параллелограмма:
Стороны равны 1, а острый угол будет равен 300:
Ответ: 0,5
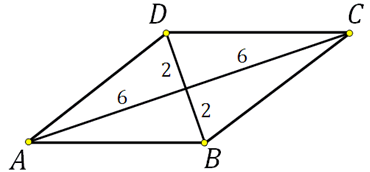
27614. Найдите площадь ромба, если его диагонали равны 4 и 12.
Известно, что диагонали ромба пересекаются под прямым углом, также они точкой пересечения делятся пополам. Построим эскиз следующим образом и отметим на нём размеры половин диагоналей:
Получается, что ромб диагоналями разбивается на 4 равных прямоугольных треугольника с катетами 2 и 6. Можем вычислить площадь этого треугольника:
Так как все четыре треугольника образованные диагоналями равны, то
Ответ: 24
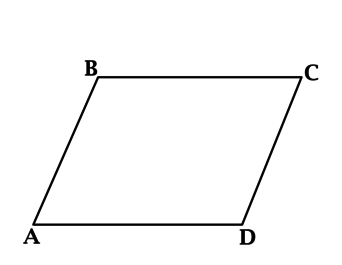
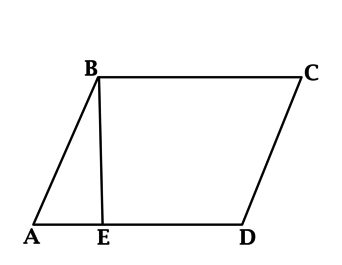
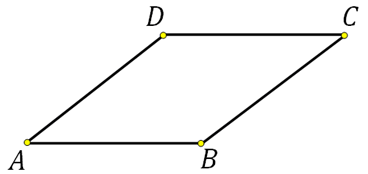
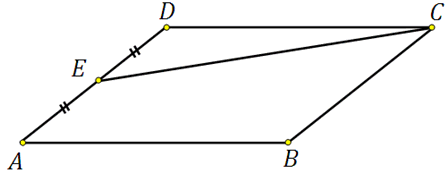
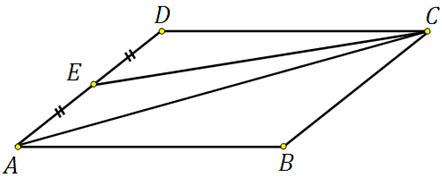
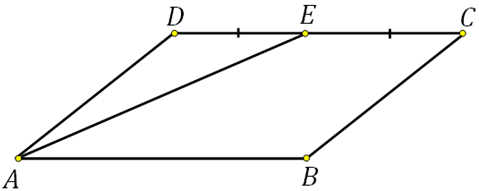
317338. Площадь параллелограмма ABCD равна 189. Точка Е середина стороны AD. Найдите площадь трапеции AECB.
Для того чтобы вычислить площадь трапеции достаточно понимать как определить площадь отсечённого треугольника EDC. *Далее мы из площади параллелограмма просто вычтем площадь треугольника.
Посмотрите! Сторона треугольника ED равна половине стороны параллелограмма, высота у них общая. Что это значит? А то что:
Получается, что площадь треугольника в четыре раза меньше площади параллелограмма:
Таким образом:
Ответ: 141,75
*Какую часть по площади занимает треугольник в параллелограмме можно увидеть разделив параллелограмм диагональю (он делится пополам):
Площадь треугольника ADC составляет ½ от площади параллелограмма, а площадь треугольника EDC равна половине площади ADC, то есть треугольник EDC по площади будет в 4 раза меньше.
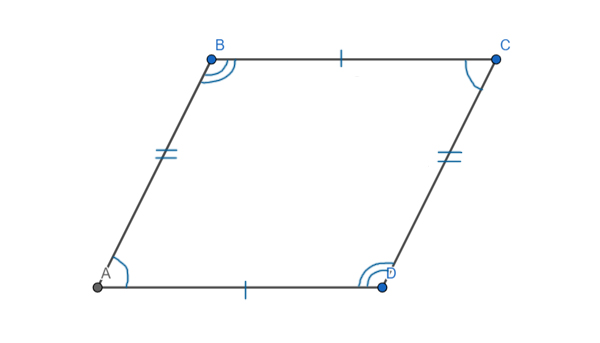
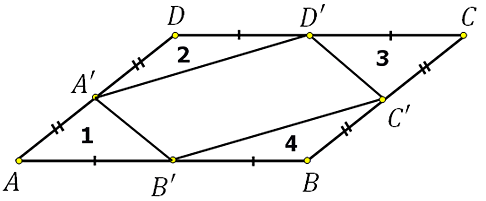
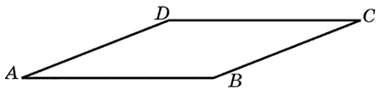
319056. Площадь параллелограмма ABCD равна 153. Найдите площадь параллелограмма A′B′C′D′, вершинами которого являются середины сторон данного параллелограмма.
Построим эскиз:
Нетрудно заметить, что площади треугольников 1, 2, 3 и 4 равны, так как у них есть равные стороны и синусы углов между ними приобретают равные значения.
Вычислим площадь треугольника АA′D′:
Получается, что площадь треугольника будет в восемь раз меньше. Таким образом, искомая площадь равна:
Ответ: 76,5
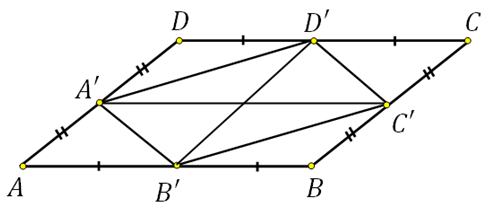
*Конечно же, «опытный глаз» сразу увидит, что площадь параллелограмма A′B′C′D′ в два раза меньше площади данного параллелограмма, но понимать формальное соотношение площадей фигур необходимо и важно.
**Если вы построите отрезки соединяющие середины противоположных сторон, то сразу наглядно увидите каким образом параллелограмм разбивается на равные по площади треугольники и решение будет очевидно.
319057. Площадь параллелограмма ABCD равна 176. Точка E– середина стороны CD. Найдите площадь треугольника ADE.
Площадь треугольника ADE составляет четвёртую часть от площади параллелограмма, посмотрите вше задачу 317338. То есть SADE=176/4=44.
Ответ: 44
27585. Найдите площадь параллелограмма, если две его стороны равны 8 и 10, а угол между ними равен 300.
Посмотреть решение
27610. Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
Посмотреть решение
27611. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.
Посмотреть решение
27612. Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
Посмотреть решение
27613. Найдите площадь ромба, если его высота равна 2, а острый угол 300.
Посмотреть решение
27615. Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
Посмотреть решение
27616. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
Посмотреть решение
На этом всё. Успеха вам!
С уважением, Александр
Делитесь информацией о сайте в социальных сетях.
0
Задания для подготовке к ОГЭ по теме: «Площадь параллелограмма»
|
Задания для подготовке к ОГЭ 8 класс Тема: Параллелограмм. Площадь. Вариант 1 |
Задания для подготовке к ОГЭ 8 класс Тема: Параллелограмм. Площадь.. Вариант 2 |
|
1) Площадь параллелограмма равна 40, а две его стороны равны 5 и 10. Найдите его высоты. В ответе укажите большую высоту. 2) Площадь параллелограмма ABCD равна 60. Точка E — середина стороны AB. Найдите площадь трапеции DAEC. 3) Найдите площадь параллелограмма, изображённого на рисунке. 4) На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь. 5) Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 45°. Найдите площадь параллелограмма, делённую на 6) Одна из сторон параллелограмма равна 50, другая равна 1, а косинус одного из углов равен 7) Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 4 и HD = 65. Диагональ параллелограмма BD равна 97. Найдите площадь параллелограмма. |
1) Площадь параллелограмма равна 36, а две его стороны равны 6 и 12. Найдите его высоты. В ответе укажите большую высоту. 2) Площадь параллелограмма ABCD равна 68. Точка E — середина стороны AB. Найдите площадь треугольника CBE. 3) Найдите площадь параллелограмма, изображённого на рисунке. 4) На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь. 5) Одна из сторон параллелограмма равна 12, другая равна 5, а один из углов — 60°. Найдите площадь параллелограмма, делённую на 6) Одна из сторон параллелограмма равна 4, другая равна 14, а косинус одного из углов равен 7) Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 5 и HD = 15. Диагональ параллелограмма BD равна 17. Найдите площадь параллелограмма. |
|
Задания для подготовке к ОГЭ 8 класс Тема: Параллелограмм. Площадь.. Вариант 3 |
Задания для подготовке к ОГЭ 8 класс Тема: Параллелограмм. Площадь.. Вариант 4 |
|
1) Площадь параллелограмма равна 48, а две его стороны равны 8 и 16. Найдите его высоты. В ответе укажите меньшую высоту. 2) Площадь параллелограмма ABCD равна 84. Точка E — середина стороны AB. Найдите площадь треугольника CBE. 3) Найдите площадь параллелограмма, изображённого на рисунке. 4) На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь. 5) Одна из сторон параллелограмма равна 12, другая равна 5, а синус одного из углов равен 6) Одна из сторон параллелограмма равна 15, другая равна 6, а тангенс одного из углов равен 7) Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 2 и HD = 12. Диагональ параллелограмма BD равна 13. Найдите площадь параллелограмма. |
1) Площадь параллелограмма равна 54, а две его стороны равны 9 и 18. Найдите его высоты. В ответе укажите меньшую высоту. 2) Площадь параллелограмма ABCD равна 76. Точка E — середина стороны AB. Найдите площадь трапеции DAEC. 3) Найдите площадь параллелограмма, изображённого на рисунке. 4) На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь. 5) Одна из сторон параллелограмма равна 18, другая равна 25, а синус одного из углов равен 6) Одна из сторон параллелограмма равна 8, другая равна 18, а тангенс одного из углов равен 7) Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 7 и HD = 24. Диагональ параллелограмма BD равна 51. Найдите площадь параллелограмма. |
Задания для подготовки:
1) Площадь параллелограмма равна 32, а две его стороны равны 8 и 16. Найдите его высоты. В ответе укажите большую высоту.
2) Площадь параллелограмма равна 56, а две его стороны равны 7 и 28. Найдите его высоты. В ответе укажите меньшую высоту.
3) Площадь параллелограмма ABCD равна 180. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
4) Площадь параллелограмма ABCD равна 132. Точка E — середина стороны AB. Найдите площадь треугольника CBE.
5) Найдите площадь параллелограмма, изображённого на рисунке.
6) На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.
7) Одна из сторон параллелограмма равна 24, другая равна 20, а синус одного из углов равен 
8) Одна из сторон параллелограмма равна 12, другая равна 5, а косинус одного из углов равен 
9) Одна из сторон параллелограмма равна 20, другая равна 29, а тангенс одного из углов равен
10) Одна из сторон параллелограмма равна 21, другая равна 15, а косинус одного из углов равен
11) Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 1 и HD = 63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
12) Стороны параллелограмма равны 10 и 85. Высота, опущенная на первую сторону, равна 51. Найдите высоту, опущенную на вторую сторону параллелограмма.
ОТВЕТЫ:
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
Вариант 4 |
|
|
1 |
8 |
6 |
3 |
3 |
|
2 |
45 |
51 |
63 |
57 |
|
3 |
40 |
28 |
20 |
44 |
|
4 |
10 |
20 |
28 |
36 |
|
5 |
30 |
30 |
20 |
200 |
|
6 |
5 |
14 |
30 |
18 |
|
7 |
4968 |
160 |
70 |
1395 |
|
8 |
33 |
1,5 |
6 |
24 |
Опубликовано 27.06.18 в 04:35
Размер файла: 43.76 Кбайт
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Параллелограмм и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства параллелограмма:
(blacktriangleright) Противоположные стороны попарно равны;
(blacktriangleright) Диагонали точкой пересечения делятся пополам;
(blacktriangleright) Противоположные углы попарно равны, а сумма соседних равна (180^circ).
Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:
(blacktriangleright) если противоположные стороны попарно равны;
(blacktriangleright) если две стороны равны и параллельны;
(blacktriangleright) если диагонали точкой пересечения делятся пополам;
(blacktriangleright) если противоположные углы попарно равны.
Площадь параллелограмма
Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.
Задание
1
#1783
Уровень задания: Легче ЕГЭ
Периметр параллелограмма равен (100), его большая сторона равна (32). Найдите меньшую сторону параллелограмма.
Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна (100 : 2 = 50), значит, меньшая сторона параллелограмма равна (50 — 32 = 18).
Ответ: 18
Задание
2
#1784
Уровень задания: Равен ЕГЭ
Периметр параллелограмма равен (15). При этом одна сторона этого параллелограмма на (5) больше другой. Найдите меньшую сторону параллелограмма.
У параллелограмма противоположные стороны равны. Пусть (BC = AB +
5), тогда периметр параллелограмма (ABCD) равен (AB + BC + CD + AD =
AB + AB + 5 + AB + AB + 5 = 4cdot AB + 10 = 15), откуда находим (AB
= 1,25). Тогда меньшая сторона параллелограмма равна (1,25).
Ответ: 1,25
Задание
3
#273
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (BE) – высота, (BE = ED = 5). Площадь параллелограмма (ABCD) равна 35. Найдите длину (AE).
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда (35 = BE cdot AD = 5cdot(5 + AE)), откуда находим (AE = 2).
Ответ: 2
Задание
4
#1785
Уровень задания: Равен ЕГЭ
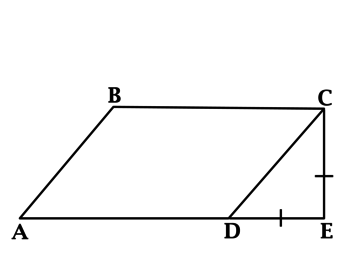
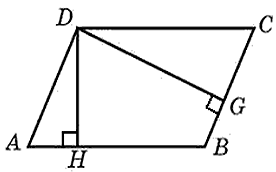
Из точки (C) параллелограмма (ABCD) опустили перпендикуляр на продолжение стороны (AD) за точку (D). Этот перпендикуляр пересёк прямую (AD) в точке (E), причём (CE = DE). Найдите (angle B) параллелограмма (ABCD). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle EDC = angle DCE). Так как (angle DEC = 90^{circ}), а сумма углов треугольника равна (180^{circ}), то (angle EDC =
45^{circ}), тогда (angle ADC = 180^{circ} — 45^{circ} =
135^{circ}). Так как в параллелограмме противоположные углы равны, то (angle B = angle ADC = 135^{circ}).
Ответ: 135
Задание
5
#1686
Уровень задания: Равен ЕГЭ
Диагональ (BD) параллелограмма (ABCD) перпендикулярна стороне (DC) и равна (4). Найдите площадь параллелограмма (ABCD), если (AD=5).
По теореме Пифагора находим: (AB^2=AD^2 — BD^2 = 25 — 16 = 9) (Rightarrow) (AB = 3). (S_{ABCD} = 4cdot3 = 12).
Ответ: 12
Задание
6
#1685
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (P_{triangle AOB} = 
(P_{triangle AOB} = AO + OB + AB), (P_{triangle AOD} = AO + OD + AD), (BO = OD) (Rightarrow) (P_{triangle AOD} — P_{triangle AOB} = AD — AB = 1), но (AD + AB = 7) (Rightarrow) (AD = 4), (AB = 3) (Rightarrow) (ADcdot AB = 12).
Ответ: 12
Задание
7
#3617
Уровень задания: Равен ЕГЭ
Стороны параллелограмма равны (9) и (15). Высота, опущенная на первую сторону, равна (10). Найдите высоту, опущенную на вторую сторону параллелограмма.
Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь (S=9cdot 10), с другой стороны, (S=15cdot h), где (h) – высота, которую нужно найти.
Следовательно, [9cdot 10=15cdot hquadLeftrightarrowquad h=6]
Ответ: 6
Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.
Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».
Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Инфоурок
›
Геометрия
›Тесты›Задачи модуля «Геометрия» ОГЭ 9 класс по теме » ПАРАЛЛЕЛОГРАММ» (с ответами).
-
Скачать материал
-
15.03.2016
11289
-
DOCX
92.1 кбайт -
206
скачиваний -
Рейтинг:
4 из 5 -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Мартышечкина Наталья Геннадьевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 8 лет и 6 месяцев
- Подписчики: 1
- Всего просмотров: 153342
-
Всего материалов:
8
Привет! Сегодня повторим геометрическую фигуру параллелограмм и порешаем задачи на эту тему.
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.
Свойства параллелограмма:
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
3. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его четырёх сторон.
Признаки параллелограмма:
1. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник — параллелограмм.
2. Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник — параллелограмм.
3. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм
Площадь параллелограмма
Площадь параллелограмма равна произведению его основания на высоту.
S = h∙a
C другой стороны, каждая диагональ параллелограмма делит его на два равных треугольника. Применив формулу для площади треугольника через синус угла, получим, что площадь параллелограмма можно вычислить следующим образом:
S = a∙b∙sinα
a и b — стороны, α — величина угола между ними
Так же, разделив двумя диагоналями параллелограмм на 4 треугольника, и использовав вышеуказанную формулу для площади треугольника через синус угла, получается, площадь параллелограмма через диагонали можно представить в виде формулы:
S = ½∙d1∙d2∙sinφ
d1 и d2 — диагонали, φ — величина угла между ними
Эта формула справедлива для любого выпуклого четырёхугольника.
Задачи на параллелограмм.
Задача (Накрест лежащие углы)
Биссектриса тупого угла ∠ABC параллелограмма ABCD делит противоположную сторону AD в соотношении 1:3, считая от вершины острого угла. Бо́льшая сторона AD равна 12. Найдите периметр параллелограмма.
Решение:
Найдём отрезок AE. Всего отрезок AD содержит 4 части (1+3), а AE — это одна часть. Тогда получается AE = AD/4 = 12/4 = 3.
Углы ∠EBC и ∠BEA равны, т.к. эти углы накрест лежащие при параллельных прямых AD и BC и секущей BE.
Т.к. ∠EBC=∠BEA=∠ABE (Ведь BE — биссектриса), следовательно, треугольник ABE — равнобедренный (два угла равны ∠BEA = ∠ABE). Значит, боковые стороны равны AB=AE=3.
Теперь можно найти и периметр. По 1 свойству параллелограмма AB=DC=3, а так же AD=BC=12.
P=(12+3)*2 = 30
Ответ: 30
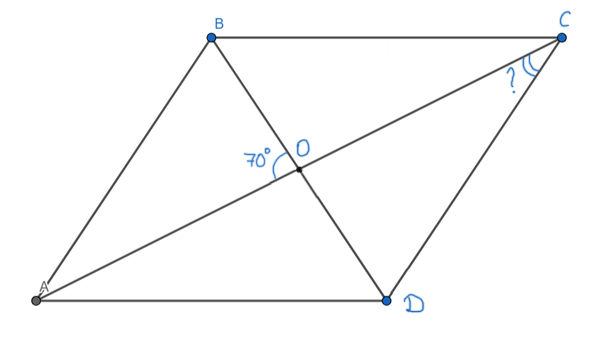
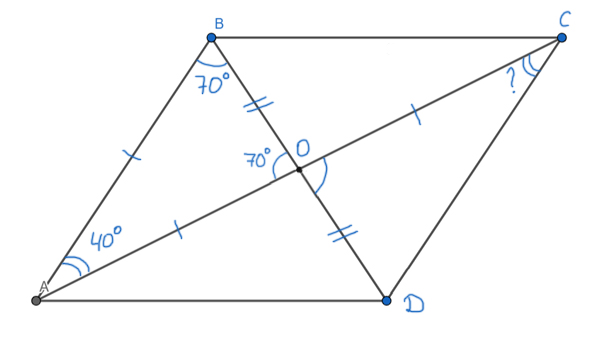
Задача (Свойство диагоналей)
В параллелограмме ABCD диагональ AC вдвое больше, чем сторона AB. Диагонали пересекаются в точке O. Угол ∠AOB=70°. Найдите угол ∠ACD. Ответ запишите в градусах.
Решение:
Воспользуемся свойством параллелограмма. Оно говорит, что диагонали параллелограмма в точке пересечения делятся пополам. Получается AO=OC=AB, т.к. AB — так же половина диагонали AC.
Получается треугольник ABO — равнобедренный. Тогда углы при основании раны ∠AOB= ∠ABO=70°. Т.к сумма углов в треугольнике ABO равна 180°, то ∠BAO = 180° — 70° — 70° = 40°.
Угол ∠BAO = ∠ОСВ (эти углы накрест лежащие при параллельных прямых AB и DC и секущей AC).
Значит, ∠BAO = ∠ОСВ = 40°.
Ответ: 40
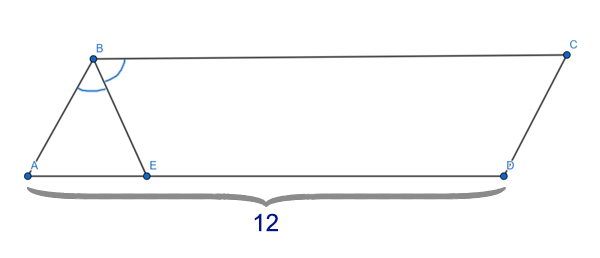
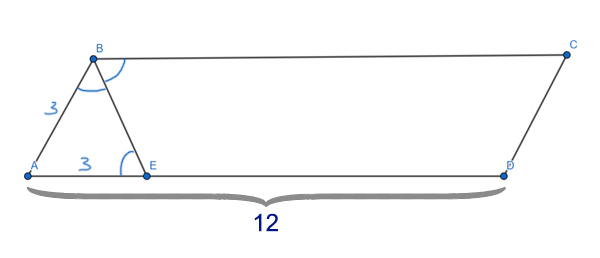
Задача (Используем параллельные прямые)
Боковая сторона равнобедренного треугольника равна 8. Из произвольной точки, на основании треугольника, проведены две прямы, параллельные боковым сторонам. Найдите периметр образовавшегося параллелограмма.
Решение:
Углы ∠KDA и ∠BCA являются соответственными при параллельных прямых KD и BC и секущей AC. Значит, они равны ∠KDA=∠BCA.
Получается, что треугольник AKD — равнобедренный. Ведь, ∠BAC=∠BCA (Т.к. это углы при основании в равнобедренном треугольнике ABC) ⇒ ∠BAC = ∠KDA, а если в треугольнике два угла равны, то такой треугольник — равнобедренный.
Чтобы найти периметр параллелограмма, достаточно найти сумму двух его пересекающихся сторон, и затем эту сумму нужно умножить на 2. Сумма двух пересекающихся сторон параллелограмма DKBM как раз равна боковой стороне треугольника ABC. Т.е. KD + KB = AB (АК=КD т.к. треугольник AKD равнобедренный).
PDKBM = 2*(KD + KB) = 2 * AB = 2 * 8 = 16
Ответ: 16
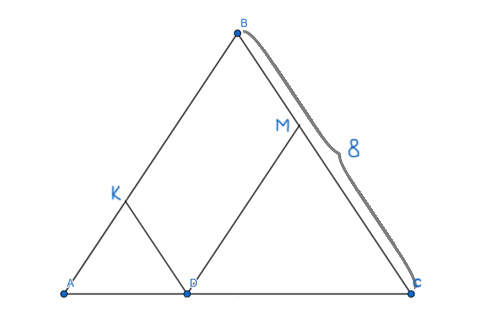
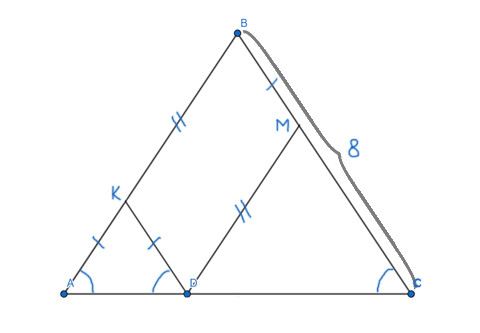
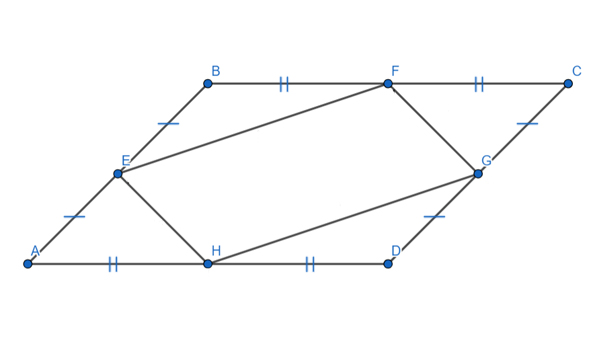
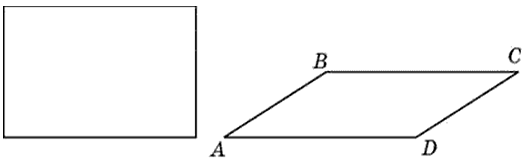
Задача (Два параллелограмма)
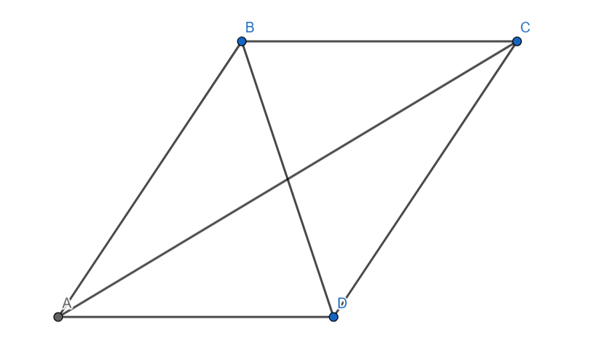
Площадь параллелограмма ABCD равна 77. Найдите площадь параллелограмма EFGH, вершинами которого являются середины сторон данного параллелограмма.
Решение:
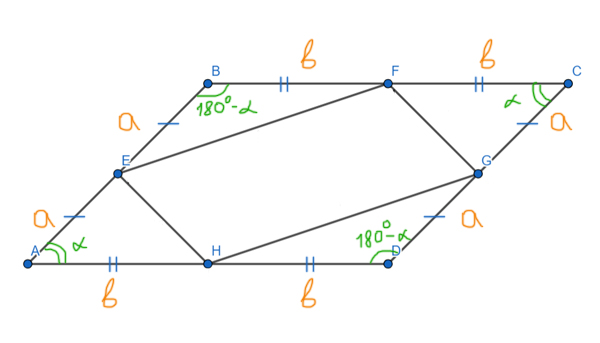
Обозначим AE=EB=CG=GD=a, BF=FC=AH=HD=b, ∠BAD=∠BCD=α, ∠ABC=∠ADC=180°-α.
Рассмотрим площади четырёх треугольников, которые получились внутри параллелограмма ABCD равны. Используем формулу для площади треугольника через синус угла.
SAEH = ½∙a∙b∙sinα
SEBF = ½∙a∙b∙sin(180°-α)
SFCG = ½∙a∙b∙sinα
SHGD = ½∙a∙b∙sin(180°-α)
Т.к. по формуле приведения sinα = sin(180°-α), то площади всех четырёх треугольников равны.
Площадь параллелограмма ABCD через синус угла α можно представить:
SABCD = AB∙AD∙sinα = 2a∙2b∙sinα = 4∙a∙b∙sinα
Тогда
SABCD — SAEH — SEBF — SFCG — SHGD =
4∙a∙b∙sinα — 4 ∙ (½∙a∙b∙sinα) = 2∙a∙b∙sinα
Получается, что если из площади параллелограмма ABCD вычесть площади четырех получившихся треугольников, то останется ровно половина от изначальной площади. Это и есть площадь параллелограмма EFGH.
SEFGH = ½ ∙ SABCD = ½ ∙ 77 = 38,5
Ответ: 38,5
Задача (Диагонали параллелограмма)
Диагонали параллелограмма равны 12 и 14. Найдите стороны параллелограмма, если их разность равна 4. В ответе запишите сумму двух его разных сторон.
Решение:
Здесь удобно воспользоваться 3 свойством, которое было описано в начале статьи.
Пусть AB=x, а BC=y.
Тогда по 3 свойству:
122 + 142 = x2 + x2 + y2 + y2
А с другой стороны, по условию
x — y = 4
x = 4 + y
Подставляем x в первое уравнение.
340 = 2∙(4+y)2 + 2∙y2
340 = 2∙(16 + 8∙y + y2) + 2∙y2
170 = 16 + 8∙y + y2 + y2
2∙y2 + 8∙y — 154 = 0
Получили квадратное уравнение.
y2 + 4∙y — 77 = 0
D = 16 + 4∙77 = 324
√D = 18
y1 = (-4 + 18)/2 = 7
y2 = (-4 — 18)/2 = -11
Отрицательное число не подходит.
x = 7 + 4 = 11.
Ответ: 18

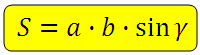
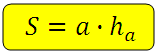

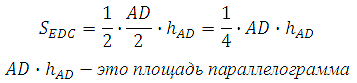
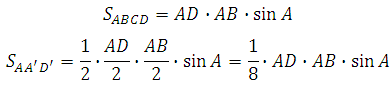







 . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.



 . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.

 . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма. . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма. 

 . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма. . Найдите площадь параллелограмма.
. Найдите площадь параллелограмма.