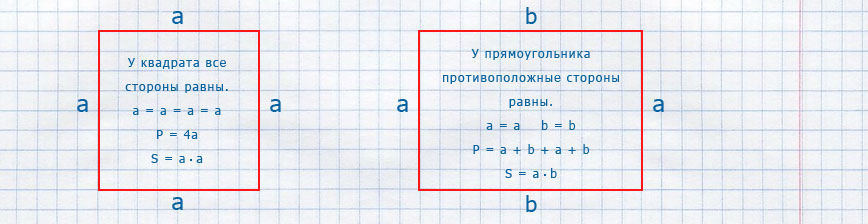
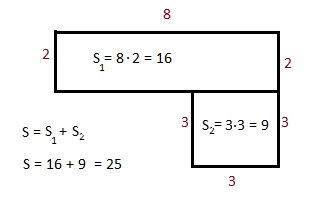Для решения задач на нахождения периметра и площади прямоугольников и квадратов необходимо освоить следующие основные формулы:
a — длина
b — ширина
P — периметр
S — площадь
Формулы площади и периметра для квадрата
P = a + a + a + a; P = a · 4 — периметр квадрата
S = a · a; S = a² — площадь квадрата
Формулы площади и периметра для прямоугольника
P = a + b + a + b; P = 2a + 2b;
P = (a + b) · 2 — периметр прямоугольника
S = a · b — площадь прямоугольника
Примеры решения задач разной сложности на нахождение периметра и площади
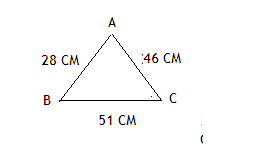
Задача 1
Каков периметр треугольника ABC?
Ответ: периметр треугольника равен 125 см.
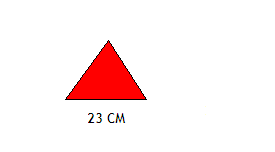
Задача 2
Красный треугольник является равносторонним со стороной 23 сантиметров. Чему равен его периметр?
Ответ: Все три стороны равностороннего треугольника равны. Таким образом, его периметр равен 23 · 3 = 69 см.
Задача 3
Равнобедренный треугольник имеет периметр 37 сантиметров, а его основание имеет длину 9 сантиметров. Каждая из двух других сторон будет иметь длину _____ см.?
Ответ: Равнобедренный треугольник имеет две равные стороны. Сумма равных сторон будет 37 — 9 = 28 см. Значит, каждая из них будет равна 28 : 2 = 14 см.
Задача 4
У Тимы есть сад в форме квадрата со стороной 9 метров. Какова длина забора, который опоясывает сад?
Ответ: Все стороны квадрата равны. Длина забора P равна длине стороны умноженной на 4. P = 4 · 9 = 36 метров.
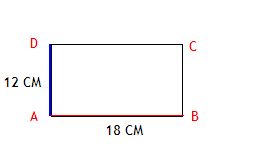
Задача 5
В прямоугольнике ABCD красная сторона составляет 18 см, а синяя сторона 12 см. Чему равен периметр прямоугольника?
Ответ: Периметр прямоугольника равен 60 см.
Задача 6
Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь?
Ответ: Площадь прямоугольника 56 м².
Задача 7
Площадь витрины квадратной формы 64м². Узнай ее периметр.
Ответ: Периметр витрины равен 32 м.
Задача 8
Длина прямоугольника 9 дм, ширина 7 см. Найдите его площадь.
Ответ: Площадь прямоугольника равна 630 см².
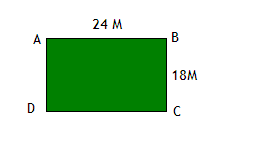
Задача 9
Парк имеет форму прямоугольника с длиной 24 метра и шириной 18 метров. Если на его сторонах надо посадить деревья с отступом в 2 метра друг от друга, то сколько нужно деревьев?
Ответ: 42 дерева.
Задача 10
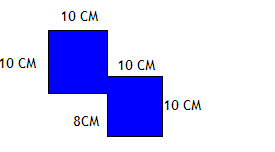
Каков периметр синей фигуры?
Ответ: Здесь есть два квадрата, у которых есть общая часть стороны. Так как сторона квадрата равна 10 см и часть стороны равна 8 см, то общая часть 2 см, а оставшаяся часть второго квадрата равна 8 см.
Периметр равен 10 + 10 + 8 + 10 + 10 + 10 + 8 + 10 = 76 см.
Задача 11
Два прямоугольных участка имеют одинаковую площадь. Длина первого — 48 м, а ширина 30 м. Чему равна длина второго участка, если его ширина на 6 м больше ширины первого участка?
Ответ: Длина второго участка 40 м.
Задача 12
Найди периметр квадрата со стороной 8 см.
Ответ: Периметр квадрата 32 см.
Задача 13
Сторона квадрата 6 см. Найди длину прямоугольника с таким же периметром и шириной 3 см.
Решение:
6 · 4 = 24 (см) -находим периметр квадрата
3 + 3 = 6 (см) -сумма ширины прямоугольника
24 — 6 = 18 (см)- сумма двух длин прямоугольника
18 : 2 = 9 (см)
Ответ: Длина прямоугольника 9 см.
Задача 14
Длина бассейна прямоугольной формы 15 м. Найди периметр бассейна, если его площадь 120 м2.
Решение:
120:15=8 (м)- ширина бассейна
(8+15)·2= 46 (м)
Ответ: Периметр бассейна 46 метров
Задача 15
Периметр квадрата 8 см. Из трех таких квадратов сложили прямоугольник. Найди периметр получившегося прямоугольника.
Решение:
8:4=2 (см)- сторона квадрата
2+2+2+2+2+2+2+2=16(см)
Ответ: Периметр прямоугольника 16 см.
Задача 16
Ученику нужно было начертить прямоугольник со сторонами 5 см и 9 см, а он начертил его со сторонами 6 и 8 см. На сколько см² он ошибся?
Решение:
5 · 9 = 45 (см²)
6 · 8 = 48 (см²)
48 — 45 = 3 (см²)
Ответ: Ученик ошибся на 3 см²
Задача 17
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.
Решение:
4·2=8 (дм) -длина окна
8·4=32 (дм²)
Ответ: Площадь окна 32 дм²
Задача 18
Один прямоугольный участок имеет длину 36 м, а ширину 20 м. Найдите ширину другого участка с такой же площадью, если его длина на 6 м меньше длины первого участка.
Ответ: Ширина другого участка 24 м.
Задача 19
У какой фигуры площадь больше и на сколько: у квадрата со стороной 4 см или у прямоугольника со сторонами 2 см и 6 см?
Ответ: Площадь квадрата больше на 4 см.
Задача 20
Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
Ответ: Площадь квадрата 36 см², периметр квадрата 24 см.
Задача 21
У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
Ответ: Площадь прямоугольника 35 м², периметр прямоугольника 24 см.
Задача 22
Сторона клумбы квадратной формы 8 м. 7/16 всей площади клумбы засажено ромашками, а остальная площадь – незабудками. На какой площади клумбы посажены незабудки?
Решение:
1) 8 ∙ 8 = 64 (площадь клумбы)
2) 64 : 16 = 4(1/16 клумбы)
3) 4 ∙ 7 = 28 (плошадь клумбы засаженая ромашками)
4) 64 – 28 = 36
Ответ: Незабудками засажено 36 м².
Задача 23
Длина прямоугольника 6 см. Чему равна его площадь, если периметр составляет 18 см?
Решение:
1) 6 ∙ 2 = 12
2) 18 – 12 = 6
3) 6 : 2 = 3 (ширина прямоугольника)
4) 3 ∙ 6 = 18
Ответ: Площадь прямоугольника 18 м².
Задача 24
Площадь прямоугольного стола 4800 кв см. Его ширина 60 см. Чему равен его периметр?
Решение:
1) 4800 : 60 = 80 (длина стола)
2) 60 ∙ 2 = 120 см
3) 80 ∙ 2 = 160 см
4) 120 + 160 = 280 см
Ответ: Периметр стола 280 см.
Задача 25
Периметр прямоугольника 40 см. Одна сторона 5 см. Чему равна его площадь?
Решение:
1) 5 ∙ 2 = 10
2) 40 – 10 = 30
3) 30 : 2 = 15 (другая сторона прямоугольника)
4) 5 ∙ 15 = 75
Ответ: Площадь прямоугольника 75 см².
Задача 26
Площадь квадрата 49 кВ дм. Узнайте его периметр.
Решение:
1) 49 : 7 = 7 (сторона квадрата)
2) 7 ∙ 4 = 28 (периметр квадрата)
Ответ: Периметр квадрата равен 28 дм.
Задача 27
Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычислите площадь окна.
Решение:
1) 4 ∙ 2 = 8 (длина окна)
2) 4 ∙ 8 = 32
Ответ: Площадь окна равна 32 м².
Задача 28
Длина участка земли 54 м. ширина — 48 м. 5/9 площади засажено картофелем. Остальная часть участка – капустой. Какая площадь засажена капустой?
Решение:
1) 54 ∙ 48 = 2592 (площадь участка земли)
2) 2592 : 9 = 288 (1/9 площади)
3) 288 ∙ 5 = 1440 (5/9 площади)
4) 2592 – 1440 = 1152
Ответ: Капустой засадили 1152 м².
Задача 29
Найди периметр квадрата со стороной 16 см.
Ответ: Периметр квадрата 64 см.
Задача 30
Найди длину прямоугольника с помощью уравнения, если его ширина 7 см, а периметр равен 40 см.
Решение:
P = (a + b) · 2 — периметр прямоугольника
или
(a + b) · 2 = P,
где a — длина = ?, b — ширина = 7 см, P — периметр = 40 см.
Составим уравнение:
(а + 7) · 2 = 40
2а + 14 = 40
2а = 40 — 14
2а = 26
а = 26 : 2
а = 13
Ответ: Длина прямоугольника 13 см.
Задача 31
Найди ширину прямоугольника, если его длина 10 см, а периметр равен 30 см.
Ответ: Ширина прямоугольника 5 см.
Задача 32
Периметр квадрата 24 см. Найди его площадь.
Решение:
24 : 4 = 6 (см)
6 · 6 = 36 (см²)
Ответ: Площадь квадрата 36 см².
Задача 33
Периметр прямоугольника 36 см. Длина его 4 см. Найди площадь прямоугольника.
Ответ: Площадь прямоугольника 56 см².
Задача 34
Площадь прямоугольника 40 см². Ширина его 4 см. Чему равен периметр прямоугольника?
Решение:
40 : 4 = 10 (см)
(10 + 4) · 2 = 28 (см)
Ответ: Периметр прямоугольника 28 см.
Задача 35
Ребро куба равно 2 сантиметров. Найти площадь всех граней куба.
Решение:
Куб — многогранник, поверхность которого состоит из шести одинаковых по площади квадратов.
У куба 8 вершин, 12 рёбер, 6 граней (поверхностей).
Если S = a · a — площадь квадрата, тогда
S = (a · a) · 6 — площадь всех граней куба, из условия задачи a = 2, тогда S = 2 · 2 · 6
2 · 2 · 6 = 24 (см²)
Ответ: Площадь всех граней куба равна 24 см².
Задача 36
Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.
Ответ: Площадь получившейся фигуры равна 44.
Задача 37
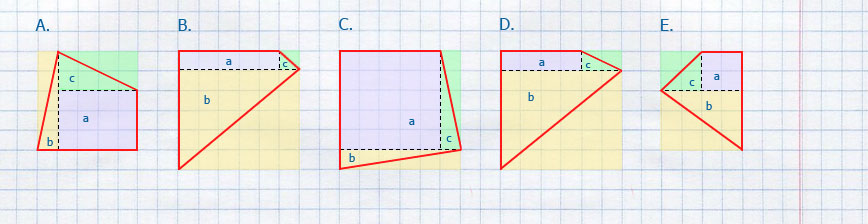
Площадь одной клетки равна 1см.
- Найдите площадь фигуры, изображённой на рисунке A.
- Найдите площадь фигуры, изображённой на рисунке B.
- Найдите площадь фигуры, изображённой на рисунке C.
- Найдите площадь фигуры, изображённой на рисунке D.
- Найдите площадь фигуры, изображённой на рисунке E.
Ответ: Площадь фигуры A 18,5 см², площадь фигуры B 20,5 см², площадь фигуры C 30,5 см², площадь фигуры A 18,5 см², площадь фигуры E 12 см².
Задача 38
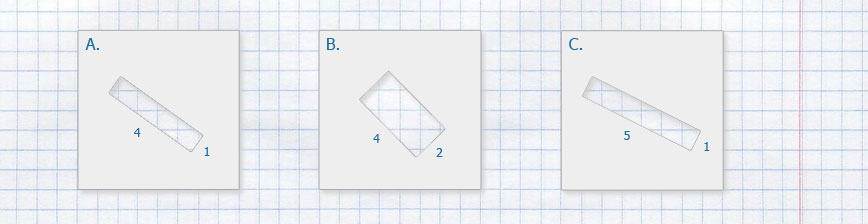
Найдите площади и периметры фигурок. Сделайте вывод.
Ответ: Пусть каждая из сторон клетки равна 1 см, тогда применив формулу площади квадрата S = a · a получим площадь одной клетки 1 · 1 = 1 см²
Фигура A — прямоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура A имеет четыре стороны, тогда 1 + 4 + 1 + 4 = 10 см — периметр фигуры.
Фигура B — квадрат состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура B имеет четыре стороны, тогда 2 + 2 + 2 + 2 = 8 см — периметр фигуры.
Фигура C — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура C имеет шесть сторон, тогда 3 + 1 + 2 + 1 + 2 + 1 = 10 см — периметр фигуры.
Фигура D — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура D имеет восемь сторон, тогда 1 + 1 + 2 + 1 + 1 + 1 + 2 + 1 = 10 см — периметр фигуры.
Фигура E — неправильный многоугольник состоящий из четырёх клеток по 1 см², тогда 1 · 4 = 4 см² — площадь фигуры; фигура E имеет восемь сторон, тогда 1 + 1 + 1 + 3 + 1 + 1 + 1 + 1 = 10 см — периметр фигуры.
Вывод: Фигуры A, B, C, D, E имеют одинаковую площадь, но наименьший периметр имеет квадрат. У разных по форме плоских фигур, с одинаковой площадью, наименьший периметр всегда имеет квадрат.
Задача 39
Квадрат в данной фигуре имеет периметр 24 см. Синий треугольник — периметр 15 см. Каков периметр красной фигуры?
Ответ: Периметр красной фигуры равен 27 см.
Задача 40
Периметр каждого из зеленых квадратов 12 см. Каков периметр большого квадрата?
Ответ: Периметр равен 36 см.
Задача 41
Площадь прямоугольника 72 см2. Какова длина и ширина прямоугольника, если ширина в 2 раза меньше, чем его длина?
Ответ: Длина прямоугольника равна 12 см. а ширина — 6 см.
Задача 42
Найти периметр прямоугольника, если сторона (катет) a = 6 см, а сторона (катет) b = 8 см.
Ответ: Периметр прямоугольника равен 24 см.
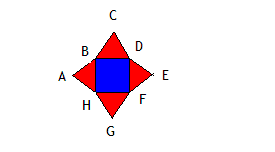
Задача 43
Периметр красного квадрата равен 16см. Красные треугольники равносторонние. Каково расстояние проползет улитка по пути ABCDFGHA?
Ответ: Расстояние пройденное улиткой будет равно 28 см.
Задача 44
В зале длиной 12 м и шириной 8 м надо покрыть пол квадратными плитками. Сколько потребуется плиток, если площадь каждой плитки 4 дм2?
Ответ: 2400 плиток.
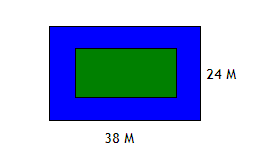
Задача 45
Каков периметр зеленой зоны, если ширина синей зоны равна 3 метра?
Ответ: Периметр зеленой зоны равен 100 метров.
Математика
Компоненты арифметических действий и их взаимосвязь.
- Компоненты при сложении:
1слагаемое, 2слагаемое, сумма.
- Компоненты при вычитании:
уменьшаемое, вычитаемое, разность.
- Компоненты при умножении:
1 множитель, 2множитель, произведение.
- Компоненты при делении:
делимое, делитель ,частное.
- Назвать результаты всех действий:
при сложении — сумма
при вычитании — разность
при умножении — произведение
при делении – частное
- Как найти неизвестное слагаемое?
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Х+4=12 или 4+х=12
Х=12-4 х=12-4
Х=8 х=8
8+4=12 4+8=12
12=12 12=12
- Как найти неизвестное уменьшаемое?
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Х-7=3
Х=3+7
Х=10
10-7=3
3=3
- Как найти неизвестное вычитаемое?
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.
8-х =5
х=8-5
х=3
8-3=5
5=5
9 Как найти неизвестный множитель?
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.
х·3=6 4·х=8
х=6:3 х=8:4
х=2 х=2
2·3=6 4·2=8
6=6 8=8
10 Как найти неизвестное делимое?
Чтобы найти неизвестное делимое, надо частное умножить на делитель.
х:5=3
х=3·5
х=15
15:5=3
3=3
- Как найти неизвестный делитель?
Чтобы найти неизвестный делитель, надо делимое разделить на частное.
6:х=2
х =6:2
х=3
6:3=2
2=2
Геометрический материал.
- Что такое квадрат?
Квадрат – это прямоугольник, у которого все стороны равны.
- Что такое прямоугольник?
Прямоугольник – это четырёхугольник, у которого все углы прямые. Противоположные стороны прямоугольника равны.
- Что такое треугольник?
Треугольник – многоугольник, у которого три угла и три стороны.
15 Что такое четырёхугольник?
Четырёхугольник – геометрическая фигура, у которой четыре угла и четыре стороны.
- Что такое периметр?
Периметр( Ρ) – это сумма длин сторон какой-нибудь геометрической фигуры.
- Что такое площадь?
Площадь(S) – это внутренняя часть какой-нибудь геометрической фигуры
(прямоугольника, квадрата и т.д)
- Как найти периметр квадрата?
У квадрата 4 стороны, равные между собой. Чтобы найти сторону квадрата, нужно Ρ□ разделить на 4.
a□ = Ρ□ : 4
- Как найти периметр прямоугольника?
Чтобы найти периметр прямоугольника, нужно сложить все 4 стороны прямоугольника
Или
сложить длину и ширину прямоугольника и умножить на 2.
Ρ▬=a+b+a+b
или
Ρ▬=(a+b)·2
- Как найти периметр треугольника?
Чтобы найти периметр треугольника, нужно сложить все 3 стороны.
- Как найти сторону квадрата, если известен периметр?
У квадрата 4 стороны, равные между собой. Чтобы найти сторону квадрата, нужно Ρ разделить на 4.
a=Ρ:4
- Как найти сторону прямоугольника, если известен периметр и другая сторона?
Чтобы найти сторону прямоугольника, нужно Ρ▬разделить на 2 и вычесть другую сторону.
a▬=Ρ▬:2 – b
b▬=Ρ▬:2 – a
22 В каких единицах измеряется периметр?
Периметр измеряется в мм, см, дм, метрах.
23 Как найти площадь квадрата?
Площадь квадрата равна произведению двух его сторон.
S□ = a · a
24 Как найти площадь прямоугольника?
Чтобы найти площадь прямоугольника, надо длину прямоугольника умножить на его ширину.
S█ = a · b
25 Как найти сторону прямоугольника, если известна площадь и другая его сторона?
Чтобы найти одну из сторон прямоугольника, нужно площадь прямоугольника разделить на известную сторону.
a▬=S▬ : b
b▬= S ▬ : a
26 В каких единицах измеряется площадь?
Площадь измеряется в квадратных единицах: мм², см², дм², м².
27 Назвать единицы длины.
Единицы длины — мм, см, дм, м, км.
28 Рассказать таблицу мер длины.
1см = 10мм
1дм = 10см
1дм = 100мм
1м = 10 дм
1м = 100 см
1км = 1000м
29 Сколько квадратных сантиметров
в 1квадратном метре?
1м² = 10 000см²
30 Сколько квадратных дециметров
в 1 квадратном метре?
1м² = 100дм²
31 Рассказать таблицу мер площади.
1м² = 100дм² = 10 000см²
1дм² = 100см² = 10 000мм²
1см² = 100мм²
Масса.
32 Назвать единицы массы.
Масса измеряется в граммах, килограммах, центнерах, тоннах.
33 Рассказать таблицу мер массы.
1кг = 1000г
1ц = 100кг
1т = 10ц
1т = 1000кг
Время.
34 Назвать единицы измерения времени.
Время измеряется секундами, минутами, часами, сутками, неделями, месяцами, годами, веками.
35 Рассказать таблицу мер времени.
1мин = 60сек.
1час = 60мин
1час = 3600сек.
1сут. = 24часа
1год = 12мес. = 365сут. или 366сут.
1век = 100лет
Взаимосвязь скорости, времени и расстояния.
36 Как найти скорость?
Чтобы найти скорость ( v ), надо расстояние ( S ) разделить на время ( t ), затраченное в пути.
v = S : t
37 Как найти время?
Чтобы найти время ( t ), надо расстояние ( S ) разделить на скорость ( v ).
t = S : v
38 Как найти расстояние?
Чтобы найти расстояние ( S ), нужно скорость ( v ) умножить на время ( t ).
S = v · t
Взаимосвязь цены, количества, стоимости.
39 Что такое цена?
Цена – стоимость одного предмета, единицы товара.
40 Как найти стоимость?
Чтобы найти стоимость, нужно цену умножить на количество.
Ст = Ц · К
41 Как найти цену?
Чтобы найти цену, нужно стоимость разделить на количество.
Ц = Ст : К
42 Как найти количество?
Чтобы найти количество, нужно стоимость разделить на цену.
К = Ст : Ц
Задачи на дроби.
43
Дробь — ⅔
2 – числитель
3 – знаменатель
44 Как найти дробь числа?
Чтобы найти дробь числа, нужно число разделить на знаменатель, а потом умножить на числитель.
45 Как найти число по дроби?
Чтобы найти число по дроби, нужно число разделить на числитель и умножить на знаменатель.
Взаимосвязь работы, времени и производительности.
46 Что такое производительность?
Как найти производительность?
Производительностью ( v ) называют работу, выполненную за единицу времени.
Чтобы найти производительность ( v ), надо всю выполненную работу разделить на время.
v = A : t
47 Как найти выполненную работу?
Выполненная работа равна производительности, умноженной на время работы.
A = v · t
48 Как найти время работы?
Чтобы узнать время работы, надо работу разделить на производительность.
t = A : v
49 Как найти среднее арифметическое?
Чтобы найти среднее арифметическое надо сумму разделить на число слагаемых.
Только факты
сайт о самом интересном вокруг нас
- Главная
- Интересные факты
- Полезные советы
- Документы
Главная » Образцы документов » Начальная школа
Памятка «Формулы площади, периметра для прямоугольника и квадрата»
02.12.2021
2244
242
Памятка в помощь ученикам начальной школы для вычисления площади и периметра для прямоугольника и квадрата. Лист с формулами и чертежами нужно распечатать и дать ребёнку.
Скачать документ
Похожие статьи:

Карточки по математике «Площадь. Единицы площади» для 3 класса
Всего 14 карточек по этой теме. Они позволят проверить полученные знания на вычисление площадей прямоугольника, используя разные единицы площади.

Итоговый тест по математике, 3 класс
Итоговый тест по математике проводится в 3 классе в конце учебного года с целью проверки знаний.

Карточки по математике «Таблица умножения и деления на 9» для 3 класса
Карточки с разными примерами на знание таблицы умножения на 9.

Карточки по математике «Таблица умножения и деления на 8» для 3 класса
Восемь карточек на проверку знания таблицы умножения и деление на число 8.

Карточки по математике «Таблица умножения и деления на 7» для 3 класса
Карточки с примерами на умножение и деление чисел на 7 для учеников 3 класса позволят проверить как ученики знают таблицу умножения.
ПЕРИМЕТР
Периметр – сумма длин всех сторон плоской геометрической фигуры. Чаще всего периметр измеряется в сантиметрах, метрах и километрах.
Чаще всего периметр обозначается буквой P.
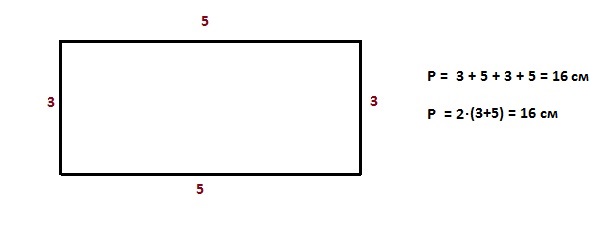
Периметр прямоугольника – удвоенная сумма длины и высоты — 2∙(a+b)
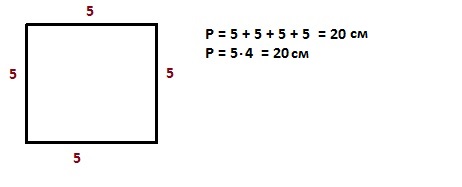
Периметр квадрата – произведение любой его стороны на 4, так как стороны равны.
ПЛОЩАДЬ
Площадь – характеристика замкнутой геометрической фигуры, которая показывает ее размер. Чаще всего площадь измеряется в квадратных сантиметрах, квадратных метрах и квадратных километрах.
В отличие от периметра, не существует универсальной формулы площади. Для каждого типа фигур площадь вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольники, квадраты и составные фигуры из прямоугольников и квадратов.
Чаще всего площадь обозначается буквой S.
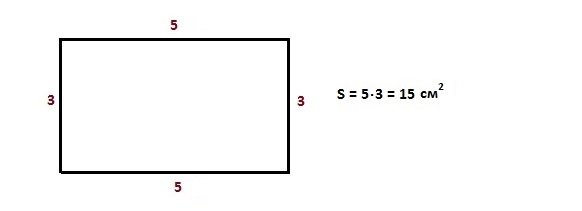
Площадь прямоугольника – произведение длины на высоту.
Хотите, чтобы ваш ребёнок обучался самостоятельно?
Вам поможет наш ВИДЕОКУРС
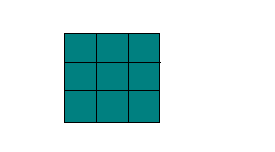
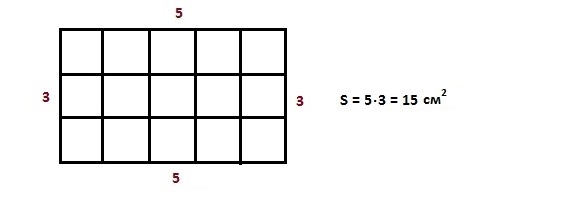
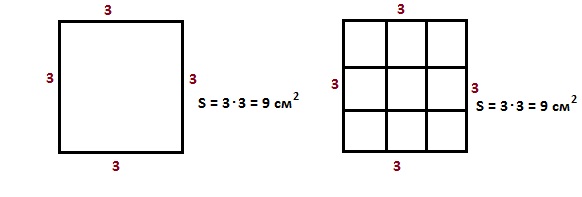
Разделим этот прямоугольник на квадраты
Мы получили 15 квадратов внутри этого прямоугольника – это и есть те самые 15 квадратных сантиметров, которые составляют площадь прямоугольника.
Площадь квадрата – произведение длины стороны на саму себя.
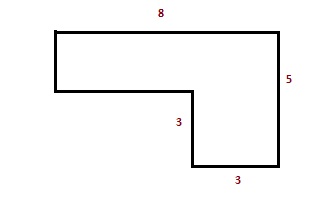
СОСТАВНЫЕ ФИГУРЫ
Разделим эту фигуру на прямоугольник и квадрат
Высота прямоугольника составит 5 – 3 = 2
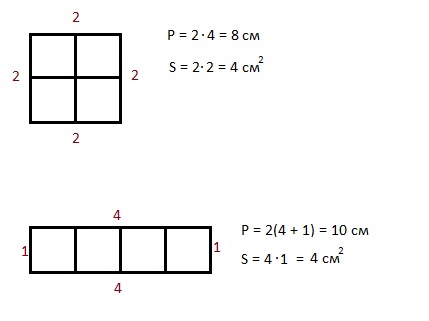
СООТНОШЕНИЕ ПЛОЩАДИ И ПЕРИМЕТРА
Фигуры с одной и той же площадью могут иметь разный периметр
Почему у нас изменился периметр, хотя площадь, т.е. число квадратиков внутри фигуры, осталась прежней?
Потому что изменилось число граней квадратиков, которые участвуют в формировании сторон фигуры, т.е. перметра. В первой фигуре – большом квадрате, в формировании сторон участвовали по две внешних грани каждого маленького квадратика – общее число таких граней 8, и периметр равен 8.
Во второй фигуре у нас в формировании сторон участвуют по три грани у двух крайних квадратиков и по две грани внутренних квадратов. Общее число таких граней 10, и периметр равен 10.
ОБЪЁМ
Объём – количественная характеристика пространства, занимаемого телом или веществом. Чаще всего объём измеряется в кубических сантиметрах, кубических дециметрах, кубических метрах и литрах.
1 л = 1 дм3
Не существует универсальной формулы объема. Для каждого типа фигур объём вычисляется по своей особой формуле. Мы будем рассматривать только прямоугольные параллелепипеды.
Чаще всего объём обозначается буквой V.
Прямоугольный параллелепипед – замкнутая фигура, у которой 6 прямоугольных граней (передняя, задняя, нижняя, верхняя и две боковые), и каждая из граней расположены под прямым углом к соседним.
Объём прямоугольного параллелепипеда – произведение его длины, ширины и высоты
Зная объём и две стороны, мы можем найти третью сторону:
c = (V:a):b = V:S
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
ЗАДАЧИ
Задача 1. Найдите периметр и площадь прямоугольника, у которого ширина 10 см, и она меньше длины на 6 см.
x = 10 см – ширина
1. Найдём длину
y = 10 + 6 = 16 см
2. Найдём периметр
P = 2∙(10+16) = 52 см
3. Найдём площадь
S = 10∙16 = 160 см2
Ответ: P = 52 см, S = 160 см2
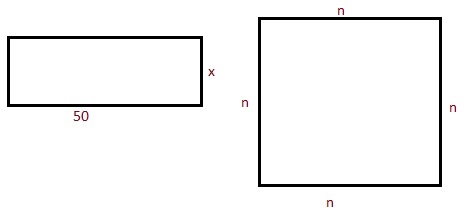
Задача 2. Какую ширину имеет прямоугольник, длина которого 50 см, а площадь совпадает с площадью квадрата периметром 80 см?
1. Вычислим сторону квадрата
4∙n = 80 — периметр
n = 20 см
2. Вычислим площадь квадрата
20∙20 = 400 см2
3. Вычислим ширину прямоугольника
50∙x = 400 см2
x = 8 см
Ответ: 8 см
Задача 3. Чему равна ширина прямоугольника, длина которого равна 15 м, а площадь 7500 дм2 ?
1 дм = 10 см, 1 м = 100 см, 1 м = 10 дм
1. Переведём длину прямоугольника в дм
x = 15∙10 = 150 дм
2. Найдём ширину прямоугольника
150∙y = 7500
y = 7500:150 = 50 дм
Ответ: 50 дм
Задача 4. Длина прямоугольника равна 60 см, и она в 3 раза больше ширины стороны.
1. Найдите площадь этого прямоугольника.
2. Найдите площадь квадрата, который имеет такой же периметр, как и прямоугольник.
3. Найдите периметр квадрата, площадь которого в 12 раз меньше площади прямоугольника.
1. Найдём ширину прямоугольника
x = 60:3 = 20 см
2. Найдём площадь прямоугольника
S = 60∙20 = 1200 см
2. Найдём периметр прямоугольника
P = 2∙(60+20) = 160 см
3. Найдём сторону квадрата
y = 160:4 = 40 см
4. Найдём площадь квадрата
Sкв = 40∙40 = 1600 см2
5. Найдём площадь квадрата, которая в 12 раз меньше площади прямоугольника:
Sкв2 = 1200:12 = 100 см2
6. Найдём сторону такого квадрата
Площадь квадрата = 100 см2
Из таблицы умножения мы знаем, что 10∙10 = 100, значит сторона квадрата = 10 см
7. Найдём периметр такого квадрата
P = 10∙4 = 40 см
ВИДЕОКУРС 2plus2.online по решению олимпиадных задач по математике для 4 класса и задач из вступительных экзаменов в 5-й класс физматшколы.
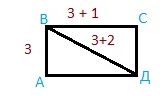
Задача 5. В прямоугольнике АВСД сторона АВ 3 см, сторона ВС на 1 см длиннее, а диагональ ВД на 2 см длиннее АВ. Найдите периметр и площадь прямоугольника АВСД и треугольника АВД.
1. Найдём сторону ВС
ВС = 3+1 = 4
2. Найдём диагональ ВД
ВД = 3+2 = 5
3. Найдём периметр АВСД
P = 2∙(3+4) = 14 см
4. Найдём площадь АВСД
Sавсд = 3∙4 = 12 см2
5. Найдём периметр треугольника АВД
Pавд = 3 + 5 + 4 = 13 см
6. Найдём площадь треугольника АВД
Треугольник АВД занимает половину площади прямоугольника АВСД
Sавд = Sавсд:2
Sавд = 12:2 = 6 см2
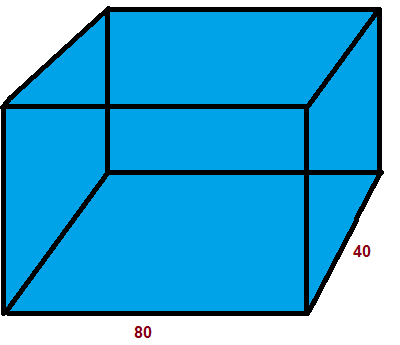
Задача 6. В аквариум в форме прямоугольного параллелепипеда, основание которого имеет стороны 80 и 40 см, налили до краёв 160 л. воды. Какова высота аквариума?
Решение
1. Переведём литры в кубические дециметры
1 л = 1 дм3, 160 л = 160 дм3
2. Переведём стороны аквариума в дециметры
1 дм = 10 см, 80 см = 8 дм, 40 см = 4 дм
3. Найдём высоту аквариума
V = a∙b∙c, a = 8, b = 4
c = (V:a):b
c = (160:8):4 = 5 дм
c = 5∙10 = 50 см
Ответ: 50 см
Загрузить PDF
Загрузить PDF
Периметр является длиной замкнутого контура геометрической фигуры, а площадь – это величина пространства, ограниченного этим замкнутым контуром.[1]
Такие математические величины, как площадь и периметр используются в повседневной жизни, в строительстве и в других областях.[2]
Например, для покраски стен вам необходимо знать, сколько краски вам понадобится, то есть нужно определить площадь окрашиваемой поверхности. Подобные вычисления производятся при строительстве забора или во время аналогичных видов деятельности.[3]
Заранее вычислив площадь и периметр, вы сэкономите время и деньги при покупке строительных материалов.
-
1
Определите форму измеряемого объекта. Периметр – это длина замкнутого контура геометрической фигуры, а для вычисления периметра фигур разной формы существуют различные формулы. Помните, что если фигура не имеет замкнутого контура, то периметр такой фигуры вычислить нельзя.
- Начните с нахождения периметра прямоугольника или квадрата (особенно, если вы делаете это впервые). Такие фигуры имеют правильную форму, что облегчает задачу нахождения их периметра.
-
2
Возьмите лист бумаги и нарисуйте на нем прямоугольник. Эту фигуру вы будете использовать для нахождения ее периметра. Убедитесь, что противоположные стороны прямоугольника имеют одинаковую длину.[4]
-
3
Измерьте ширину прямоугольника (то есть измерьте «короткую» сторону прямоугольника). Это можно сделать при помощи линейки или рулетки. Запишите значение ширины (возле «короткой» стороны). Например, ширина прямоугольника равна 3 см.
- Если вы измеряете периметр небольшой фигуры, в качестве единиц измерения используйте сантиметры, а если больших предметов – метры.
- Помните, что противоположные стороны прямоугольника равны, поэтому нужно измерить только длину двух смежных сторон.[5]
-
4
Измерьте длину прямоугольника (то есть измерьте «длинную» сторону прямоугольника). Это можно сделать при помощи линейки или рулетки. Запишите значение длины (возле «длинной» стороны).
- Например, длина прямоугольника равна 5 см.
-
5
Запишите соответствующие значения возле противоположных сторон. Помните, что в прямоугольнике 4 стороны, а противоположные стороны прямоугольника равны.[6]
Запишите значения длины и ширины прямоугольника (в приведенном примере 5 см и 3 см) у противоположных сторон. -
6
Для вычисления периметра сложите значения всех сторон. То есть в случае прямоугольника напишите: длина + длина + ширина + ширина.
- В приведенном примере периметр равен: 3 + 3 + 5 + 5 = 16 см.[7]
- Также вы можете воспользоваться следующей формулой: периметр прямоугольника = 2* (длина + ширина) (эта формула верна, так как в прямоугольнике две пары одинаковых сторон). В приведенном примере: (5+3)*2 = 8*2 = 16 см.
- В приведенном примере периметр равен: 3 + 3 + 5 + 5 = 16 см.[7]
-
7
К разным фигурам применяйте различные формулы. Для вычисления периметра фигуры другой формы потребуется соответствующая формула. В реальной жизни для нахождения периметра предмета любой формы просто измерьте его стороны. Также вы можете воспользоваться следующими формулами для вычисления периметра стандартных геометрических фигур:
- Квадрат: периметр = 4 * сторона.
- Треугольник: периметр = сторона 1 + сторона 2 + сторона 3.
- Неправильный многоугольник: периметр равен сумме всех сторон многоугольника.
- Круг: длина окружности = 2 х π х радиус = π х диаметр. [8]
- π – это число пи (константа, примерно равная 3,14). Если на вашем калькуляторе есть клавиша «π», воспользуйтесь ею для выполнения более точных вычислений.[9]
- Радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности. Диаметр – это длина отрезка, проходящего через центр окружности и соединяющего любые две точки, лежащие на этой окружности.[10]
[11]
- π – это число пи (константа, примерно равная 3,14). Если на вашем калькуляторе есть клавиша «π», воспользуйтесь ею для выполнения более точных вычислений.[9]
Реклама
-
1
Найдите значения сторон данной вам фигуры или предмета. Например, нарисуйте прямоугольник (или используйте прямоугольник, который вы нарисовали в предыдущей главе). В приведенном примере для вычисления площади прямоугольника необходимо найти его длину и ширину.
- Для измерения длины и ширины прямоугольника воспользуйтесь линейкой или рулеткой. В приведенном примере воспользуемся значениями сторон прямоугольника из предыдущей главы, а именно ширина = 3 см, длина = 5 см.
-
2
Суть площади геометрической фигуры. Вычисление площади, ограниченной замкнутым контуром, подобно разбиению внутреннего пространства фигуры на квадраты размером 1 единица х 1 единица. Имейте в виду, что площадь фигуры может быть больше или меньше периметра этой фигуры.
- Вы можете разбить данную вам фигуру на единичные квадраты (1 см х 1 см или 1 м х 1 м), чтобы визуализировать процесс вычисления площади фигуры.
-
3
Перемножьте длину и ширину прямоугольника. В приведенном примере: площадь = 3 * 5 = 15 квадратных сантиметров. Помните, что площадь измеряется в квадратных единицах измерения (квадратные километры, квадратные метры, квадратные сантиметры и так далее).
- Вы можете записать единицы измерения площади в следующем виде:
- километры²/км²
- метры²/м²
- сантиметры²/см²
- Вы можете записать единицы измерения площади в следующем виде:
-
4
К разным фигурам применяйте различные формулы. Для вычисления площади фигуры другой формы потребуется соответствующая формула. Вы можете воспользоваться следующими формулами для вычисления площади стандартных геометрических фигур:
- Параллелограмм: площадь = основание х высота
- Квадрат: площадь = сторона 1 х сторона 2
- Треугольник: площадь = ½ х основание х высота
- В некоторых учебниках эта формула выглядит так: S = ½аh.
- Круг: площадь = π х радиус²
- Радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности. Квадрат радиуса – это значение радиуса, умноженное само на себя.[12]
[13]
- Радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности. Квадрат радиуса – это значение радиуса, умноженное само на себя.[12]
Реклама
Советы
- Приведенные в этой статье формулы для вычисления площади и периметра применимы к двумерным фигурам. Если вам нужно найти объем трехмерной фигуры, например, конуса, куба, цилиндра, призмы или пирамиды, найдите соответствующую формулу в учебнике или в интернете.
Реклама
Что вам понадобится
- Бумага
- Карандаш
- Калькулятор (по желанию)
- Рулетка (по желанию)
- Линейка (по желанию)
Об этой статье
Эту страницу просматривали 237 067 раз.