Как найти площадь периметр треугольника 3 класс

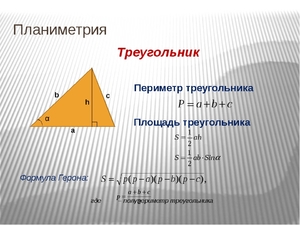
Периметр и площадь треугольника

• Периметр
• Площадь

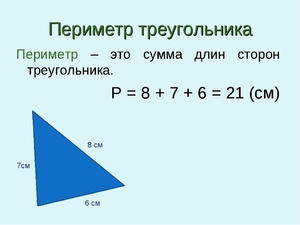
Периметр

Периметр любого треугольника равен сумме длин трёх его сторон. Общая формула для нахождения периметра треугольников:

P = a + b + c,

где  P  — это периметр треугольника,  a,  b  и  c  — его стороны.

Периметр равнобедренного треугольника можно найти сложив последовательно длины его сторон или умножив длину боковой стороны на 2 и прибавив к произведению длину основания. Общая формула для нахождения периметра равнобедренных треугольников будет выглядеть так:

P = 2a + b,

где  P  — это периметр равнобедренного треугольника,  a  — любая из боковых сторон,  b  — основание.

Периметр равностороннего треугольника можно найти сложив последовательно длины его сторон или умножив длину любой его стороны на 3. Общая формула для нахождения периметра равносторонних треугольников будет выглядеть так:

P = 3a,

где  P  — это периметр равностороннего треугольника,  a  — любая из его сторон.

Площадь

Для измерения площади треугольника можно сравнить его с параллелограммом. Рассмотрим треугольник  ABC:

Если взять равный ему треугольник и приставить его так, чтобы получился параллелограмм, то получится параллелограмм с той же высотой и основанием, что и у данного треугольника:

В данном случае общая сторона сложенных вместе треугольников является диагональю образованного параллелограмма. Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.

Так как площадь параллелограмма равна произведению его основания на высоту, то площадь треугольника будет равна половине этого произведения. Значит для  ΔABC  площадь будет равна

Теперь рассмотрим прямоугольный треугольник:

Два равных прямоугольных треугольника можно сложить в прямоугольник, если прислонить их друг к другу гипотенузой. Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:

Из это можно сделать вывод, что площадь любого прямоугольного треугольника равна произведению катетов, разделённому на 2.

Из данных примеров можно сделать вывод, что площадь любого треугольника равна произведению длин основания и высоты, опущенной на основание, разделённому на 2.

Общая формула площади треугольника:

где  S  — это площадь треугольника,  a  — его основание,  h_a  — высота, опущенная на основание  a.

Математика

Компоненты арифметических действий и их взаимосвязь.

1. Компоненты при сложении:

1слагаемое, 2слагаемое, сумма.

1. Компоненты при вычитании:

уменьшаемое, вычитаемое, разность.

1. Компоненты при умножении:

1 множитель, 2множитель, произведение.

1. Компоненты при делении:

делимое, делитель ,частное.

1. Назвать результаты всех действий:

при сложении — сумма

при вычитании — разность

при умножении — произведение

при делении – частное

1. Как найти неизвестное слагаемое?

Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.

Х+4=12                        или                4+х=12

Х=12-4                                        х=12-4                                        

Х=8                                                 х=8

8+4=12                                        4+8=12

  12=12                                        12=12

1. Как найти неизвестное уменьшаемое?

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

Х-7=3

Х=3+7

Х=10

10-7=3

        3=3

1. Как найти неизвестное вычитаемое?

Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

8-х =5

х=8-5

х=3

8-3=5

   5=5

9                Как найти неизвестный множитель?        

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

х·3=6                                4·х=8

х=6:3                                х=8:4

х=2                                х=2        

2·3=6                                4·2=8

   6=6                                   8=8

10           Как найти неизвестное делимое?

Чтобы найти неизвестное делимое, надо частное умножить на делитель.

х:5=3

х=3·5

х=15

15:5=3

     3=3

1. Как найти неизвестный делитель?

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

6:х=2

х =6:2

х=3

6:3=2

   2=2

Геометрический материал.

1. Что такое квадрат?

Квадрат – это прямоугольник, у которого все стороны равны.

1. Что такое прямоугольник?

Прямоугольник – это четырёхугольник, у которого все углы прямые. Противоположные стороны прямоугольника  равны.

1. Что такое треугольник?

Треугольник – многоугольник, у которого три угла и три стороны.

15     Что такое четырёхугольник?

Четырёхугольник – геометрическая фигура, у которой четыре угла и четыре стороны.

1. Что такое периметр?

Периметр( Ρ) – это сумма длин сторон какой-нибудь геометрической фигуры.

1. Что такое площадь?

Площадь(S) – это внутренняя часть какой-нибудь геометрической  фигуры

(прямоугольника, квадрата и т.д)

1. Как найти периметр квадрата?

У квадрата 4 стороны, равные между собой. Чтобы найти сторону квадрата, нужно Ρ□ разделить на 4.

a□ = Ρ□ : 4

1. Как найти периметр прямоугольника?

Чтобы найти периметр прямоугольника, нужно сложить все 4 стороны   прямоугольника

 Или

сложить длину и ширину прямоугольника и умножить на 2.

        Ρ▬=a+b+a+b

или

    Ρ▬=(a+b)·2

1. Как найти периметр треугольника?

Чтобы найти периметр треугольника, нужно сложить все 3 стороны.

1. Как найти сторону квадрата, если известен периметр? 

У квадрата 4 стороны, равные между собой. Чтобы найти сторону квадрата, нужно Ρ разделить на 4.

a=Ρ:4

1.         Как найти сторону прямоугольника, если известен периметр и другая сторона? 

Чтобы найти сторону прямоугольника, нужно Ρ▬разделить на 2  и  вычесть другую сторону.

a▬=Ρ▬:2 – b

b▬=Ρ▬:2 – a

22        В каких единицах измеряется периметр?

    Периметр измеряется в мм, см, дм, метрах.

23         Как найти площадь квадрата?

Площадь квадрата равна произведению двух его сторон.

S□ =  a · a

24          Как найти площадь прямоугольника?

Чтобы найти площадь прямоугольника, надо длину прямоугольника умножить на его ширину.

S█ =  a · b

25          Как найти сторону прямоугольника, если известна площадь и другая его сторона?

Чтобы найти одну из сторон прямоугольника,  нужно площадь прямоугольника разделить на известную сторону.

a▬=S▬ :  b

b▬= S ▬ : a

   26        В каких единицах измеряется площадь?

   Площадь измеряется в квадратных единицах: мм², см², дм², м².

27      Назвать единицы длины.

Единицы длины — мм, см, дм, м, км.

28           Рассказать таблицу мер длины.

1см  =  10мм

1дм  =  10см

1дм  =  100мм

1м  =    10 дм

1м  =  100 см

1км = 1000м

29       Сколько  квадратных сантиметров

в 1квадратном метре?

1м²  =  10 000см²  

30      Сколько  квадратных  дециметров  

в 1 квадратном  метре?

1м²  =  100дм²  

31            Рассказать  таблицу мер площади.

1м²  =  100дм²  = 10 000см²  

1дм²  = 100см²  =  10 000мм²

1см²  =  100мм²

Масса.

32            Назвать единицы массы.

Масса измеряется в граммах, килограммах, центнерах, тоннах.

33           Рассказать таблицу мер массы.

1кг  = 1000г

1ц  =  100кг

1т  =  10ц

1т  =  1000кг

Время.

34        Назвать  единицы измерения времени.

Время  измеряется секундами, минутами, часами, сутками, неделями, месяцами, годами, веками.

35           Рассказать таблицу мер времени.

1мин  =  60сек.

1час  =  60мин

1час  =  3600сек.

1сут.  =  24часа

1год  =  12мес.  =  365сут.  или  366сут.

1век  =  100лет

Взаимосвязь скорости, времени и расстояния.

36     Как  найти  скорость?

Чтобы найти скорость ( v ), надо расстояние ( S ) разделить на время ( t ), затраченное в пути.

v = S : t

37    Как найти время?

Чтобы найти время ( t ), надо расстояние ( S ) разделить на скорость ( v ).

t = S : v

38    Как найти расстояние?

Чтобы найти расстояние ( S ),  нужно скорость ( v ) умножить на время ( t ).

S = v · t

Взаимосвязь цены, количества, стоимости.

39    Что такое цена?

Цена – стоимость одного предмета, единицы товара.

40     Как найти стоимость?

Чтобы найти стоимость, нужно цену умножить на количество.

Ст = Ц · К

41     Как найти цену?

Чтобы найти цену, нужно стоимость разделить на количество.

Ц  =  Ст : К

42   Как найти  количество?

Чтобы найти количество, нужно стоимость разделить на цену.

К = Ст : Ц

Задачи на дроби.

43

Дробь  — ⅔

2 – числитель

3 – знаменатель

44  Как найти дробь числа?

Чтобы найти дробь числа, нужно число разделить на знаменатель, а потом умножить на числитель.

45      Как найти число по дроби?

Чтобы  найти число по дроби, нужно число разделить на числитель и умножить на знаменатель.

Взаимосвязь работы, времени и производительности.

46    Что такое производительность?

         Как найти производительность?

Производительностью ( v ) называют работу, выполненную за единицу времени.

Чтобы найти производительность ( v ), надо всю выполненную работу разделить на время.

v  =  A  :  t

47    Как найти выполненную работу?

Выполненная работа равна производительности, умноженной на время работы.

A  =  v  · t

48   Как найти время работы?

Чтобы узнать время работы, надо работу разделить на производительность.

t  =  A  :  v

49   Как  найти среднее арифметическое?

Чтобы найти среднее арифметическое надо сумму разделить на число слагаемых.

Треугольник это геометрическая фигура (многоугольник), ограниченная со всех сторон замкнутой ломаной линией, состоящая из трех отрезков.

Формула периметра треугольника

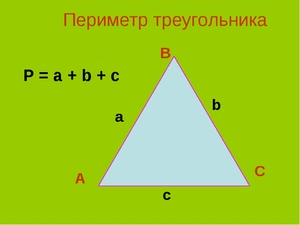
Периметр треугольника равняется сумме всех его сторон: P = a + b + c,
где P это периметр и a, b, c – стороны треугольника.

Расчет периметра треугольника

Формула площади треугольника

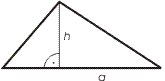
1. Самая простая формула для расчета площади это произведение основания и высоты треугольника, поделенное на 2: S = (a · h)/2,
где S это площадь, a – основание, h – высота.

Расчет:

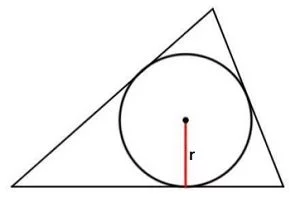
2. Вторая формула для расчета площади треугольника: по радиусу вписанной окружности и периметру: S = (r · P)/2 = r · p,
где r это радиус вписанной окружности, P – периметр треугольника, p – половина периметра треугольника (p = P/2)

Расчет:

3. Площадь треугольника по двум сторонам и углу между ними: S = a · b · sin γ)/2 = (b · c · sin α)/2 = (a · c · sin β)/2,
где a, b, c это стороны треугольника и α, β, γ – его внутренние углы.

Расчет:

4. Формула Герона или площадь треугольника по его трем сторонам: S = √p · (p — a)(p — b)(p — c),
где a, b и c это стороны треугольника и p – половина периметра треугольника.

Расчет:

Что такое периметр треугольника?

Периметром треугольника называется сумма длин всех его сторон.

Как найти/вычислить периметр треугольника?

Для получения периметра треугольника нужно сложить все его стороны: P = a + b + c,
где P это периметр и a, b, c – стороны треугольника.

Чему равен периметр треугольника?

Периметр треугольника равен сумме всех его сторон.

Как найти/посчитать площадь треугольника?

Для того, чтобы вычислить площадь треугольника, можно использовать одну из формул ее вычисления, используя доступные вводные данные.

1. произведение основания и высоты треугольника, поделенное на 2: S = (a · h)/2,
   где S это площдаь, a – основание, h – высота.
2. по радиусу вписанной окружности и периметру: S = (r · P)/2 = r · p,
   где r это радиус вписанной окружности, P – периметр треугольника, p – половина периметра треугольника (p = P/2)
3. по двум сторонам и углу между ними: S = a · b · sin γ)/2 = (b · c · sin α)/2 = (a · c · sin β)/2,
   где a, b, c это стороны треугольника и α, β, γ – его внутренние углы.
4. по трем сторонам: S = √p · (p — a)(p — b)(p — c),
   где a, b и c это стороны треугольника и p – половина периметра треугольника.

Выбирайте формулу в зависимости от известных величин.

1. Как найти периметр треугольника, зная три стороны

Просто посчитайте сумму всех сторон.

• P — искомый периметр;
• a, b, c — стороны треугольника.

2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности

Умножьте площадь треугольника на 2.

Разделите результат на радиус вписанной окружности.

• P — искомый периметр;
• S — площадь треугольника;
• r — радиус вписанной окружности.

3. Как вычислить периметр треугольника, зная две стороны и угол между ними

Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:

• Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
• Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
• Найдите корень из результата.

Теперь прибавьте к найденной стороне две ранее известные стороны.

• P — искомый периметр;
• b, c — известные стороны треугольника;
• ɑ — угол между известными сторонами;
• a — неизвестная сторона треугольника.

4. Как найти периметр равностороннего треугольника, зная одну сторону

Умножьте сторону на 3.

• P — искомый периметр;
• a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).

5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание

Умножьте боковую сторону на 2.

Прибавьте к результату основание.

• P — искомый периметр;
• a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
• b — основание треугольника (это сторона, которая отличается длиной от остальных).

6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту

Найдите квадраты боковой стороны и высоты.

Отнимите от первого числа второе.

Найдите корень из результата и умножьте его на 2.

Прибавьте к полученному числу две боковые стороны.

• P — искомый периметр;
• a — боковая сторона треугольника;
• h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).

7. Как вычислить периметр прямоугольного треугольника, зная катеты

Найдите квадраты катетов и посчитайте их сумму.

Извлеките корень из полученного числа.

Прибавьте к результату оба катета.

• P — искомый периметр;
• a, b — катеты треугольника (стороны, которые образуют прямой угол).

8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу

Посчитайте квадраты гипотенузы и катета.

Отнимите от первого числа второе.

Найдите корень из результата.

Прибавьте катет и гипотенузу.

• P — искомый периметр;
• a — любой катет прямоугольника;
• c — гипотенуза (сторона, которая лежит напротив прямого угла).

Периметр и площадь треугольника

Периметр

Периметр любого треугольника равен сумме длин трёх его сторон. Общая формула для нахождения периметра треугольников:

где P — это периметр треугольника, a, b и c — его стороны.

Периметр равнобедренного треугольника можно найти сложив последовательно длины его сторон или умножив длину боковой стороны на 2 и прибавив к произведению длину основания. Общая формула для нахождения периметра равнобедренных треугольников будет выглядеть так:

где P — это периметр равнобедренного треугольника, a — любая из боковых сторон, b — основание.

Периметр равностороннего треугольника можно найти сложив последовательно длины его сторон или умножив длину любой его стороны на 3. Общая формула для нахождения периметра равносторонних треугольников будет выглядеть так:

где P — это периметр равностороннего треугольника, a — любая из его сторон.

Площадь

Для измерения площади треугольника можно сравнить его с параллелограммом. Рассмотрим треугольник ABC:

Если взять равный ему треугольник и приставить его так, чтобы получился параллелограмм, то получится параллелограмм с той же высотой и основанием, что и у данного треугольника:

В данном случае общая сторона сложенных вместе треугольников является диагональю образованного параллелограмма. Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.

Так как площадь параллелограмма равна произведению его основания на высоту, то площадь треугольника будет равна половине этого произведения. Значит для ΔABC площадь будет равна

Теперь рассмотрим прямоугольный треугольник:

Два равных прямоугольных треугольника можно сложить в прямоугольник, если прислонить их друг к другу гипотенузой. Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:

Из это можно сделать вывод, что площадь любого прямоугольного треугольника равна произведению катетов, разделённому на 2.

Из данных примеров можно сделать вывод, что площадь любого треугольника равна произведению длин основания и высоты, опущенной на основание, разделённому на 2.

Общая формула площади треугольника:

где S — это площадь треугольника, a — его основание, h_a — высота, опущенная на основание a.

Формулы определения периметра, площади и сторон треугольника

Треугольник — это элементарная геометрическая фигура, содержащая минимально возможное количество составляющих — три.

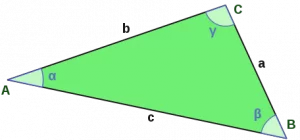
Точки соприкосновения сторон являются вершинами его углов, обозначаются заглавными латинскими символами A; B и C. Отрезки между вершинами являются сторонами или гранями треугольника и обозначаются названиями этих вершин: AB; BC; CA или прописной буквой противолежащего угла (вершины): AB=c; BC=a; CA=b.

Периметр равен длине всех сторон фигуры, у треугольника он равен сумме трех сторон:

Высота треугольника — это перпендикуляр от прямой, на которой лежит основание, до одноименной вершины, обозначается h.

Площадь составляет величину поверхности, заключенной внутри фигуры, обозначается S. Произведение основания на высоту дает значение площади. Ее можно определить и по формуле Герона:

Из этого видео вы узнаете, как найти площадь треугольника.

Классификация треугольников

Треугольник состоит из сторон и углов, сумма его углов всегда равна 180 градусов: A+B+C=180°.

1. Равноугольный: все вершины равны 60°, будет и равносторонним.
2. Равнобедренный: при равенстве двух граней углы на основании равны.
3. Разноугольный: все вершины разные, ребра у него тоже разные.
4. Прямоугольный: один угол равен 90°, примыкающие грани называются катеты, противолежащая — гипотенуза. Бывает равнобедренным (катеты равны) или разноугольным (катеты разные).
5. Тупоугольный: один угол больше 90°. Может быть равнобедренным или разноугольным.

Описание

Чтобы описать любой треугольник, достаточно указать:

1. Одну сторону и прилегающие к ней углы.
2. Две стороны и угол между ними.
3. Три стороны.

Данных из любого пункта достаточно для построения заданной фигуры и вычисления всех ее параметров, используя теорему косинусов:

Подставляя известные значения, получим уравнение, решив которое узнаем неизвестные величины.

Cos90°=0, поэтому для прямоугольного треугольника c*c=a*a+b*b, где a и b — катеты, c — гипотенуза, сторона, лежащая напротив прямого угла.

Примеры

Известно, что одна грань равна 9 см и прилегающие углы по 60 градусов. Тогда из того, что сумма углов всегда равна 180°, получаем: 180=60+60+x; x=180—120=60. Все три вершины по 60°, значит, все стороны равны. Периметр составляет P=9+9+9=27 см, полупериметр p=13,5 см. Чтобы найти высоту, нужно опустить перпендикуляр из вершины на основание, получим прямоугольный треугольник с гипотенузой 9 см, катетом 4,5 см и катетом неизвестной длины, равным искомой высоте: 9*9—4,5*4,5=60,75=h 2 .

Высота равна корню квадратному из 60,75 или 7,79422863406 см. Умножаем основание на высоту, делим пополам и получаем площадь: 7,79422863406*9/2=35,074028853 см 2 . Если находить площадь по формуле Герона через полупериметр и ребра, ответ будет одинаковый:

S=√(13,5·(13,5—9)·(13,5—9)·(13,5—9))=35,074028853 см 2 .

Следующий пример с разносторонним треугольником. Дано: AB=12 см, BC=10 см, CA=8 см. Требуется найти периметр и площадь фигуры. P=a+b+c=BC+CA+AB=10 см+8 см+12 см=30 см. Площадь находим по формуле Герона, подставляя в нее уже известные значения, учитывая, что p=0,5Р; p=15 см. S=√(p·(p—a)·(p—b)·(p—c))=√(15·(15—10)·(15—8)·(15—12))=√15·5·7·3=√1575=39,686269666 см 2 .

Рассмотрим пример, когда известны два катета прямоугольного треугольника. Допустим, они имеют значения два и четыре метра. Тогда гипотенуза будет равна корню квадратному из суммы квадратов катетов √2 2 +4 2 =4,472135955 м. Периметр 2+4+4,472135955=10,472135955. Площадь равна половине произведения катетов S=2·4=8м 2 .

Когда известны две стороны и угол между ними, остается найти только третью сторону по теореме косинусов. Пусть известные стороны составляют значения 16 и 28 метров, а угол между ними будет в 60 градусов, тогда третья сторона будет равна корню квадратному из этого выражения 16 2 +28 2 — 2·16·28·0,5, что составит значение в 24,3310501212 м. Периметр равен 16+28+24,3310501212=68,3310501212≈68,33 м. Полупериметр будет 34,165 м. Подставляя полученные значения в формулу Герона, найдем площадь S=√(34,165·(34,165—16)·(34,165—28)·(34,165—24,33))=193,982314238 м 2 .

Если известно три параметра любого треугольника — два угла и сторона или две стороны и угол между ними, то ничего особенно сложного в нахождении неизвестных параметров треугольника — периметра, площади или высоты — нет. Нужно только внимательно производить простые вычисления. Иногда можно проявить и смекалку, разбив фигуру на несколько более простых в вычислении, например, прямоугольных треугольников. В каждом конкретном случае все зависит от исходных данных. Все формулы и вычисления, приведенные выше, верны для плоских фигур; для расположенных на сферической поверхности ход вычислений будет иным.

Видео

Это видео поможет вам закрепить полученные знания.

Площадь и периметр треугольника

Треугольник это геометрическая фигура (многоугольник), ограниченная со всех сторон замкнутой ломаной линией, состоящая из трех отрезков.

Периметр

Периметр треугольника равняется сумме всех его сторон: P = a + b + c,
где P это периметр и a, b, c – стороны треугольника.

Расчет периметра

Площадь треугольника

1. Самая простая формула для расчета площади это произведение основания и высоты треугольника, поделенное на 2: S = (a · h)/2,
где S это площдаь, a – основание, h – высота.

2. Вторая формула для расчета площади: по радиусу вписанной окружности и периметру: S = (r · P)/2 = r · p,
где r это радиус вписанной окружности, P – периметр треугольника, p – половина периметра треугольника (p = P/2)

Расчет:

3. Площадь треугольника по двум сторонам и углу между ними: S = a · b · sin γ)/2 = (b · c · sin α)/2 = (a · c · sin β)/2,
где a, b, c это стороны треугольника и α, β, γ – его внутренние углы.

4. Формула Герона или площадь треугольника по его трем сторонам: S = √ p · (p — a)(p — b)(p — c) ,
где a, b и c это стороны треугольника и p – половина периметра треугольника.