Как найти площадь перпендикулярного сечения наклонной призмы - Исправление недочетов и поиск решений вместе с Examum.ru

«Геометрическое тело призма» — Прямоугольный параллелепипед. Прямоугольник. Диагональные сечения. Теорема Пифагора. Сумма площадей. Вершины. Основание призмы. Как называется призма изображённая на рисунке. Математический бой. Решение. Призма. Какая призма называется прямой. Полученные знания. Диагональ правильной треугольной призмы.

«Фигура призма» — Определение призмы. Наклонная и прямая призма. Докажем сначала теорему для треугольной призмы. Виды призм. Объем наклонной призмы. Призма. Площадь боковой поверхности призмы. Площадь полной поверхности призмы. Докажем теперь теорему для произвольной призмы. Правильная призма.

«Объём призмы» — Площадь S основания исходной призмы. Решение задачи. Цели урока. Объем исходной призмы равен произведению S · h. Объем прямой призмы. Призму можно разбить на прямые треугольные призмы с высотой h. Понятие призмы. Проведение высоты треугольника ABC. Вопросы. Изучение теоремы об объеме призмы. Основные шаги при доказательстве теоремы прямой призмы?

«Понятие призмы» — Площадь полной поверхности призмы. Прямая призма. Площадь боковой поверхности призмы. Многоугольник. Сечения призмы. Правильная призма. Призмы встречающиеся в жизни. Треугольные призмы. Доказательство. Объем наклонной призмы. Определение призмы. Наклонная и прямая призма. Виды призм. Призма.

«Свойства призмы» — Существую ли наклонные призмы, в которые можно вписать сферу. Свойства призмы. Условие, сформулированное для прямой призмы. Цилиндр. Призма. Сечение цилиндра. Формула трех косинусов. Основание. Треугольная призма. Теорема синусов для трехгранного угла. Ребро треугольной призмы. Вокруг каких из разновидностей призм всегда можно описать сферу.

«Понятие многогранника призмы» — В сечении образуется параллелограмм. Следствие. Свойства призмы. Термин “призма” греческого происхождения и буквально означает “отпиленное” (тело). Площадь поверхности призмы и площадь боковой поверхности призмы. Такое сечение называется диагональным сечением призмы. Дано: Сторона основания правильной треугольной призмы равна 8 см, боковое ребро — 6 см.

«Объём тел» — Ф(x). Ф(х1). Объем наклонной призмы, пирамиды и конуса. Ф(хi). Ф(х2). a x b x. При а =х и b=x в сечение может вырождаться точка, например, при х = а.

«Объем понятия» — 1.Площадь полной поверхности куба равна 6 м2. Или объём прямоугольного параллелепипеда равен произведению площади основания на высоту. Объём цилиндра равен произведению площади основания на высоту. В ходе урока проводится дифференцированная проверочная работа с использованием тестов. Объёмы геометрических тел.

«Объёмы» — Упражнение 7. Упражнение 8*. Боковые ребра равны 3 и составляют с плоскостью основания угол 45о. Объем наклонной призмы 3. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60о. Объем наклонной призмы 1. Ответ: Плоскость, проходящая через центры симметрии параллелепипедов. Принцип Кавальери.

«Объёмы тел» — Объём пирамиды равен одной трети произведения основания на высоту. Объём пирамиды. Объём цилиндра. 2010 г. h. V=1/3S*h. Объемы подобных тел. V=a*b*c. Объём прямой призмы. Объемы тел. Следствие. Объём наклонной призмы. Объём наклонной призмы равен произведению площади основания на высоту. Объём цилиндра равен произведению площади основания на высоту.

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Сегодня мы выведем формулу объема наклонной призмы с помощью интеграла.

Вспомним, что такое призма и какая призма называется наклонной?

ПРИЗМА — многогранник, две грани которого (основания) — равные многоугольники, расположенные в параллельных плоскостях, а другие грани (боковые) — параллелограммы.

Если боковые ребра призмы перпендикулярны плоскости основания, то призма прямая, в противном случае призма называется наклонной.

Объем наклонной призмы равен произведению площади основания на высоту.

1) Рассмотрим треугольную наклонную призму ВСЕВ2С2Е2. Объем данной призмы равен V, площадь основания — S, высота — h.

Воспользуемся формулой: объем равен интеграл от 0 до h S от икс дэ икс.

V= , где площадь перпендикулярного оси Ох сечения. Выберем ось Ох, причем точка О — начало координат и лежит в плоскости ВСЕ (нижнее основание наклонной призмы). Направление оси Ох перпендикулярно плоскости ВСЕ. Тогда ось Ох пересечет плоскость в точке h, и проведем плоскость Е1 параллельную основаниям наклонной призмы и перпендикулярную оси Ох. Поскольку плоскости параллельны и боковые грани — это параллелограммы, то ВЕ= , СЕ=С1Е1=С2Е2; ВС=В1С1=В2С2

Откуда следует, что треугольники ВСЕ = E2 равны по трем сторонам. Если треугольники равны, значит, равны их площади. Площадь произвольного сечения S(х) равна площади основания Sосн.

В данном случае площадь основания является постоянной. В качестве пределов интегрирования возьмем 0 и h. Получаем формулу: объем равен интеграл от 0 до h S от икс дэ икс или интеграл от 0 до h площади основания от икс дэ икс, площадь основания — это константа (постоянная величина), мы можем вынести ее за знак интеграла и получится, что интеграл от 0 до h дэ икс равен аш минус 0:

Получается, что объем наклонной призмы равен произведению площади основания на высоту.

2) Докажем эту формулу для произвольной n- угольной наклонной призмы. Для доказательства возьмем пятиугольную наклонную призму. Выполним разбиения наклонной призмы на несколько треугольных призм, в данном случае — на три (так же, как при доказательстве теоремы об объеме прямой призмы). Обозначим объем наклонной призмы за V. Тогда объем наклонной призмы будет состоять из суммы объемов трех треугольных призм (по свойству объемов).

V=V1+V2+V3, а объем треугольной призмы мы ищем по формуле: объем наклонной призмы равен произведению площади основания на высоту.

Значит, объем наклонной призмы равен сумме произведений площадей основания на высоту, выносим высоту h за скобки (так как она одинаковая у трех призм) и получаем:

Теорема доказана.

Боковое ребро наклонной призмы — 4 см, составляет с плоскостью основания угол 30°.Стороны треугольника, которые лежат в основании, равны 12, 12, и 14 см. Найти объем наклонной призмы.

Дано: — наклонная призма,

АВ = 12 см, ВС = 12 см, АС = 14 см, В = 4 см, BK = 30° .

Найти: V — ?

Дополнительное построение: В наклонной призме проведем высоту Н.

Мы знаем, что объем наклонной призмы равен произведению площади основания на высоту.

В основании наклонной призмы лежит произвольный треугольник, у которого известны все стороны, значит, применим формулу Герона: площадь треугольника равна квадратному корню из произведения пэ на разность пэ и а, на разность пэ и бэ, на разность пэ и цэ, где пэ — полупериметр треугольника, который ищем по формуле: половина суммы всех сторон а, в и с:

считаем полупериметр:

Подставим значение полупериметра в формулу площади основания, упростим и получим ответ: семь корней из 95.

Рассмотрим ΔB H. Он прямоугольный, так как Н — высота наклонной призмы. Из определения синуса, катет равен произведению гипотенузы на синус противолежащего угла

значение синус 30° равен одной второй, значит

Мы узнали, что

А высота Н — высота наклонной призмы — равна 2.

Следовательно, объем равен

Умение определять объем пространственных фигур является важным для решения геометрических и практических задач. Одной из таких фигур является призма. Рассмотрим в статье, что она собой представляет, и покажем, как вычислять объем наклонной призмы.

Что понимают под призмой в геометрии?

Речь идет о правильном полиэдре (многограннике), который образован двумя одинаковыми основаниями, находящимися в параллельных плоскостях, и несколькими параллелограммами, соединяющими отмеченные основания.

Основаниями призмы могут быть произвольные многоугольники, например, треугольник, четырехугольник, семиугольник и так далее. Причем число углов (сторон) многоугольника определяет название фигуры.

Любая призма, имеющая в основании n-угольник (n — число сторон), состоит из n+2 граней, 2 × n вершин и 3 × n ребер. Из приведенных чисел видно, что количества элементов призмы соответствуют теореме Эйлера:

3 × n = 2 × n + n + 2 — 2

Ниже рисунок показывает, как выглядят треугольные и четырехугольные призмы, сделанные из стекла.

Виды фигуры. Наклонная призма

Выше уже было сказано, что название призмы определяется числом сторон многоугольника в основании. Однако существуют и другие особенности в ее строении, определяющие свойства фигуры. Так, если все параллелограммы, образующие боковую поверхность призмы, представлены прямоугольниками или квадратами, то такая фигура называется прямой. Для расстояние между основаниями равно длине бокового ребра любого прямоугольника.

Если же некоторые или все боковые стороны являются параллелограммами, то речь идет о наклонной призме. Высота ее уже будет меньше, чем длина бокового ребра.

Еще один критерий, по которому проводят классификацию рассматриваемых фигур — это длины сторон и углы многоугольника в основании. Если они равны друг другу, то многоугольник будет правильным. Прямая фигура с правильным многоугольником в основаниях называется правильной. С ней удобно работать при определении площади поверхности и объема. Наклонная призма в этом плане представляет некоторые трудности.

На приведенном рисунке показаны две призмы, имеющие четырехугольное основание. Угол 90° показывает принципиальную разницу между прямой и наклонной призмой.

Формула для определения объема фигуры

Часть пространства, ограниченная гранями призмы, называется ее объемом. Для рассматриваемых фигур любого типа эту величину можно определить по следующей формуле:

Здесь символом h обозначена высота призмы, которая является мерой дистанции между двумя основаниями. Символ S o — одного основания площадь.

Площадь основания найти несложно. Учитывая тот факт, является правильным многоугольник или нет, а также зная количество его сторон, следует применить соответствующую формулу и получить S o . Например, для правильного n-угольника с длиной стороны a площадь будет равна:

S n = n / 4 × a 2 × ctg (pi / n)

Теперь перейдем к высоте h. Для прямой призмы определение высоты не представляет никаких трудностей, однако для призмы наклонной — это непростая задача. Решать ее можно различными геометрическими методами, отталкиваясь от конкретных начальных условий. Тем не менее существует универсальный способ определения высоты фигуры. Опишем его кратко.

Идея заключается в нахождении расстояния от точки в пространстве до плоскости. Предположим, что плоскость задана уравнением:

A × x+ B × y + C × z + D = 0

Тогда от точки с координатами (x 1 ; y 1 ; z 1) плоскость будет находиться на расстоянии:

h = |A × x 1 + B × y 1 + C × z 1 + D| / √ (A 2 + B 2 + C 2)

Если координатные оси расположить так, что точка (0; 0; 0) будет лежать в плоскости нижнего основания призмы, тогда уравнение для плоскости основания можно записать так:

Это означает, что формула для высоты запишется так:

Достаточно найти координату z любой точки верхнего основания, чтобы определить высоту фигуры.

Пример решения задачи

На рисунке ниже дана Основанием наклонной призмы является квадрат со стороной 10 см. Необходимо вычислить ее объем, если известно, что длина бокового ребра равна 15 см, а острый угол фронтального параллелограмма равен 70°.

Поскольку высота h фигуры также является высотой параллелограмма, то используем формулы для определения его площади, чтобы найти h. Обозначим стороны параллелограмма так:

Тогда можно записать для него следующие формулы для определения площади S p:

S p = a × b × sin (α);

Откуда получаем:

Здесь α — острый угол параллелограмма. Поскольку основанием является квадрат, то формула объема наклонной призмы примет вид:

V = a 2 × b × sin (α)

Подставляем из условия данные в формулу и получаем ответ: V ≈ 1410 см 3 .

Объем является характеристикой любой фигуры, имеющей ненулевые размеры во всех трех измерениях пространства. В данной статье с точки зрения стереометрии (геометрии пространственных фигур) мы рассмотрим призму и покажем, как находить объемы призм различного вида.

Стереометрия располагает точным ответом на этот вопрос. Под призмой в ней понимают фигуру, образованную двумя многоугольными одинаковыми гранями и несколькими параллелограммами. На рисунке ниже показаны четыре разные призмы.

Каждую из них можно получить следующим образом: необходимо взять многоугольник (треугольник, четырехугольник и так далее) и отрезок определенной длины. Затем каждую вершину многоугольника следует перенести с помощью параллельных отрезков в другую плоскость. В новой плоскости, которая будет параллельна исходной, получится новый многоугольник, аналогичный выбранному изначально.

Призмы могут иметь разный тип. Так, они могут быть прямыми, наклонными и правильными. Если боковое ребро призмы (отрезок, соединяющий вершины оснований) перпендикулярно основаниям фигуры, то последняя является прямой. Соответственно, если это условие не выполняется, то речь идет о наклонной призме. Правильная фигура — это прямая призма с равноугольным и равносторонним основанием.

Объем правильных призм

Начнем с самого простого случая. Приведем формулу объема призмы правильной, имеющей n-угольное основание. Формула объема V для любой фигуры рассматриваемого класса имеет следующий вид:

То есть для определения объема достаточно рассчитать площадь одного из оснований S o и умножить ее на высоту h фигуры.

В случае правильной призмы обозначим длину стороны ее основания буквой a, а высоту, которая равна длине бокового ребра, буквой h. Если основание n-угольник правильный представляет, то для расчета его площади проще всего воспользоваться следующей универсальной формулой:

S n = n/4*a2*ctg(pi/n).

Подставляя в равенство значение числа сторон n и длину одной стороны a, можно вычислить площадь n-угольного основания. Отметим, что функция котангенса здесь вычисляется для угла pi/n, который выражен в радианах.

Учитывая записанное для S n равенство, получаем конечную формулу объема призмы правильной:

V n = n/4*a2*h*ctg(pi/n).

Для каждого конкретного случая можно записать соответствующие формулы для V, но все они однозначно следуют из записанного общего выражения. Например, для четырехугольной призмы правильной, которая в общем случае является прямоугольным параллелепипедом, получаем:

V 4 = 4/4*a2*h*ctg(pi/4) = a2*h.

Если в этом выражении принять h=a, то мы получаем формулу для объема куба.

Объем прямых призм

Отметим сразу, что для прямых фигур не существует общей формулы для вычисления объема, которая была приведена выше для правильных призм. При нахождении рассматриваемой величины следует использовать исходное выражение:

Здесь h — это длина бокового ребра, как и в предыдущем случае. Что касается площади основания S o , то она может принимать самые разные значения. Задача расчета у прямой призмы объема сводится к нахождению площади ее основания.

Расчет величины S o следует проводить, исходя из особенностей самого основания. Например, если оно является треугольником, тогда площадь вычислить можно так:

Здесь h a — апофема треугольника, то есть его высота, опущенная на основание a.

Если основанием является четырехугольник, то он может быть трапецией, параллелограммом, прямоугольником или иметь совершенно произвольный тип. Для всех названых случаев следует воспользоваться соответствующей формулой планиметрии для определения площади. Например, для трапеции эта формула имеет вид:

S o4 = 1/2*(a 1 + a 2)*h a .

Где h a — высота трапеции, a 1 и a 2 — это длины ее параллельных сторон.

Чтобы определить площадь для многоугольников более высокого порядка, следует разбивать их на простые фигуры (треугольники, четырехугольники) и рассчитывать сумму площадей последних.

Объем наклонных призм

Это самый сложный случай расчета объема призмы. Общая формула для таких фигур также применима:

Тем не менее, к сложности нахождения площади основания, представляющего многоугольник произвольного типа, добавляется проблема определения высоты фигуры. Она в наклонной призме всегда меньше длины бокового ребра.

Проще всего эту высоту найти, если известен какой-либо угол фигуры (плоский или двугранный). Если такой угол дан, тогда следует с его использованием построить внутри призмы прямоугольный треугольник, который бы содержал в качестве одной из сторон высоту h и, пользуясь тригонометрическими функциями и теоремой Пифагора, найти величину h.

Геометрическая задача на определение объема

Дана правильная призма с треугольным основанием, имеющая высоту 14 см и длину стороны 5 см. Чему равен объем треугольной призмы?

Поскольку речь идет о правильной фигуре, то мы вправе воспользоваться известной формулой. Имеем:

V 3 = 3/4*a2*h*ctg(pi/3) = 3/4*52*14*1/√3 = √3/4*25*14 = 151,55 см3.

Треугольная призма является достаточно симметричной фигурой, в форме которой часто выполняют разные архитектурные сооружения. Эту призму из стекла используют в оптике.

Понятие о призме. Формулы объема призм разного типа: правильной, прямой и наклонной. Решение задачи — все о путешествиях на сайт

Источник

ВИДЕОУРОК

Призма называется наклонной, если её боковые рёбра не
перпендикулярны к плоскости основания.

Если в наклонной призме боковое ребро образует одинаковые
углы со сторонами основания, которые выходят из его одного конца, то проекция
ребра на плоскость основания будет биссектрисою соответственного угла основания.

Если в наклонной призме две смежные боковые грани образуют
одинаковые двугранные углы с основанием, то проекция на основание бокового
ребра, которое принадлежит линии пересечения двух граней указанных двугранных углов,
будет биссектрисою угла основания.

Поверхность наклонной призмы.

Боковою поверхностью наклонной призмы называется сумма
площадей всех её боковых граней.

Полною поверхностью наклонной призмы называется сумма её боковой
поверхности и площадей оснований.

S_п = S_б + 2S_осн.

Боковая поверхность наклонной призмы равна произведению
периметра перпендикулярного сечения на боковое ребро.

S_б = P_пер × AA₁,

где P_пер – периметр сечения, перпендикулярного к боковому
ребру.

ЗАДАЧА:

В наклонной призме проведено сечение,
перпендикулярное боковым рёбрам и пересекающее все боковые рёбра. Найдите площадь
боковой поверхности призмы, если периметр сечения равен р,
а боковое ребра равно l.

РЕШЕНИЕ:

Пусть в наклонной призме
проведено сечение, перпендикулярное боковым рёбрам, и пересекающее все боковые
рёбра (сечение KLM). Плоскость
проведенного сечения разбивает призму на две части.

Применим к одной из них параллельное
перемещение, которое совмещает основания призмы. При этом получим прямую
призму, основанием которой будет сечение данной призмы, а боковые ребра равны l. Эта
призма имеет туже самую боковую поверхность, что и данная. Таким образом, площадь
боковой поверхности данной призмы равна рl.

ЗАДАЧА:

В наклонной треугольной призме боковые
рёбра равны 8
см; стороны перпендикулярного сечения относятся как

9 : 10 : 17,

а его площадь равна 144
см². Найдите
боковую поверхность этой призмы.

РЕШЕНИЕ:

Пусть дана призма АС₁;

АА₁ = ВВ₁ =
СС₁ =
8 см,

А₂В₂С₂ – перпендикулярное сечение призмы, притом

А₂В₂ : В₂С₂ : С₂ А₂ = 9 : 10 : 17 і

Необходимо определить боковую
поверхность призмы:

S_бок = (А₂В₂ + В₂С₂ + С₂ А₂) × АА₁.

По условию задачи

АА₁ =
8 см, а

А₂В₂ : В₂С₂ : С₂ А₂ = 9 : 10 : 17.

Обозначим:

А₂В₂ = 9х, В₂С₂ = 10х, С₂А₂ = 17х.

Тогда по формуле Герона площадь
перпендикулярного сечения будет равно:

а по условию она равна 144
см²,
то есть

36х² =
144, откуда х = 2 см.

В таком случае

А₂В₂ + В₂С₂ + С₂ А₂

= 36х = 72 см,

то есть

S_бок = 72 × 8 см² = 576 см².

ОТВЕТ: 576 см²

Задания к уроку 3

Задание 1
Задание 2
Задание 3

Другие уроки:

Урок 1. Прямые и плоскости в пространстве
Урок 2. Прямая призма
Урок 4. Правильная призма
Урок 5. Параллелепипед
Урок 6. Прямругольный параллелепипед
Урок 7. Куб
Урок 8. Пирамида
Урок 9. Правильная пирамида
Урок 10. Усечённая пирамида
Урок 11. Цилиндр
Урок 12. Вписанная и описанная призмы
Урок 13. Конус
Урок 14. Усечённый конус
Урок 15. Вписанная и описанная пирамиды
Урок 16. Сфера и шар
Урок 17. Комбинация тел

Источник

Многогранник, две грани которого равные -угольники, лежащие в параллельных плоскостях, а остальные граней – параллелограммы, называют -угольной призмой.

Два -угольника называют основаниями призмы, а параллелограммы – боковыми гранями. Стороны граней называют ребрами призмы, а концы ребер – вершинами призмы.

На рисунке 9.41 изображена пятиугольная призма, на рисунке 9.42 – треугольная, а на рисунке 9.43 – четырехугольная.

На рисунке 9.42 треугольники и – основания призмы , параллелограммы , , – боковые грани, отрезки , , – боковые ребра, отрезки , , , , , – ребра оснований, точки , , , , , – вершины призмы.

Если грани призмы не имеют общего ребра, то их называют противоположными, если грани имеют общее ребро, то – смежными. На рисунке 9.43 грани и , и , а также и являются противоположными, а, например, грани и – смежными.

Две вершины призмы, не принадлежащие одной грани, называют противоположными. Например, на рисунке 9.43 вершины и – противоположные.

Диагональю призмы называют отрезок, соединяющий две противоположные вершины (например, диагональ на рисунке 9.41).

Треугольная призма не имеет противоположных граней, не имеет противоположных вершин и не имеет диагоналей.

Прямой призмой называют призму, боковые ребра которой перпендикулярны плоскостям ее оснований (рис. 9.42). Боковые грани прямой призмы – прямоугольники.

Наклонной призмой называют призму, боковые ребра которой являются наклонными к плоскостям ее оснований (рис. 9.41 и 9.43). Боковые грани наклонной призмы – параллелограммы (некоторые боковые грани могут быть и прямоугольниками).

Высотой призмы называют перпендикуляр, заключенный между основаниями призмы. Высота прямой призмы равна длине ее бокового ребра (рис. 9.42), высота наклонной призмы – не равна (рис. 9.41 и 9.43).

Диагональным сечением призмы называют сечение, содержащее диагональ призмы. На рисунке 9.44 построены диагональные сечения и четырехугольной призмы .

Параллелепипедом называют призму, основание которой – параллелограмм (рис. 9.44).

Прямым параллелепипедом называют параллелепипед, боковые ребра которого перпендикулярны плоскостям его оснований (рис. 9.45).

Прямоугольным параллелепипедом называют прямой параллелепипед, основанием которого является прямоугольник. На рисунке 9.46 изображен прямоугольный параллелепипед.

Свойство диагонали прямоугольного параллелепипеда: квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений:

, (9.1)

где , , – длины ребер, выходящих из одной вершины, – диагональ параллелепипеда.

Объем прямоугольного параллелепипеда находят по формуле:

. (9.2)

Кубом называют прямоугольный параллелепипед с равными ребрами. Все грани куба – квадраты (рис. 9.47).

Объем куба с ребром находят по формуле:

. (9.3)

Площадь поверхности куба с ребром находят по формуле:

$LaTeX formula: S_{n.}=6a^2$ . (9.4)

Диагональ куба с ребром а находят по формуле:

. (9.5)

Объем прямой призмы высоты и периметром основания находят по формуле:

$LaTeX formula: V=S_{o.} cdot h$ . (9.6)

Площадь поверхности прямой призмы находят по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ . (9.7)

Площадь боковой поверхности прямой призмы высоты и периметром основания находят по формуле:

$LaTeX formula: S_{delta .}=P_{o.} cdot h$ . (9.8)

Объем наклонной призмы можно вычислить по формуле:

$LaTeX formula: V=S_{o.} cdot h$ . (9.9)

Площадь поверхности наклонной призмы можно вычислить по формуле:

$LaTeX formula: S_{n.}=2S_{o.}+S_{delta .}$ , (9.10)

а также по формулам:

$LaTeX formula: V=S_{c.} cdot l$ , (9.9.1)

$LaTeX formula: S_{delta.}=P_{c.} cdot l$ , (9.10.1)

где сечение, перпендикулярное ребру (рис. 9.48).

Правильной призмой называют прямую призму, основанием которой является правильный многоугольник.

Пример 1. Найдите объем и площадь поверхности куба, зная, что его диагональ см.

Решение. Согласно формуле 9.5 и см. По формуле 9.3 $LaTeX formula: V=(2sqrt{3})^2=24sqrt{3}$ ( $LaTeX formula: _{CM}\^3$ ), а по формуле 9.4 $LaTeX formula: S_{n.}=6 cdot (2sqrt{3})^2=72$ ( $LaTeX formula: _{CM}\^2$ ).

Ответ: $LaTeX formula: _{CM}\^3$ ; $LaTeX formula: _{CM}\^2$ .

Пример 2. Найдите объем прямоугольного параллелепипеда, диагональ которого равна , а его измерения относятся как .

Решение. Согласно условию задачи запишем измерения параллелепипеда: , , .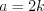

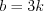
Согласно свойству диагонали прямоугольного параллелепипеда 9.1, получим: , , откуда . Тогда , , .

Зная три измерения параллелепипеда, по формуле 9.2 найдем его объем: .

Ответ: .

Пример 3. В основании прямой призмы лежит прямоугольный треугольник с катетами см и см. Высота призмы равна см. Найдите площадь поверхности и объем призмы.

Решение. 1. Площадь треугольника с катетами и найдем по формуле $LaTeX formula: S=frac{1}{2}ab$ . Получим: $LaTeX formula: S=frac{1}{2} cdot 10 cdot 8=40$ ( $LaTeX formula: _{CM}\^2$ ).

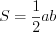
2. Гипотенузу найдем по теореме Пифагора: (см).

3. Площадь боковой поверхности призмы найдем по формуле 9.8 : $LaTeX formula: S_{delta .}=(10+8+2sqrt{41}) cdot 8=16(9+sqrt{41})$ ( $LaTeX formula: _{CM}\^2$ ).

4. Согласно формуле 9.7 , найдем площадь полной поверхности призмы:

$LaTeX formula: S_{n.}=2 cdot 40+16(9+sqrt{41})=16(14+sqrt{41})$ ( $LaTeX formula: _{CM}\^2$ ).

5. Объем призмы найдем по формуле 9.6 :

( $LaTeX formula: _{CM}\^3$ ).

Ответ: $LaTeX formula: _{CM}\^2$ ; $LaTeX formula: _{CM}\^3$ .

Пример 4. Объем наклонной треугольной призмы равен , а боковое ребро . Правильный треугольник – сечение, перпендикулярное боковому ребру (рис. 9.49). Найдите площадь боковой поверхности этой призмы.

Решение. 1. Согласно формуле 9.9.1 запишем: $LaTeX formula: 270=S_{c.} cdot 10$ , откуда $LaTeX formula: S_{c.}=27$ .

2. Площадь правильного треугольника со стороной находят по формуле $LaTeX formula: S=frac{sqrt{3}a^2}{4}$ . Тогда $LaTeX formula: 27=frac{sqrt{3}a^2}{4}$ , $LaTeX formula: a^2=9cdot 4cdot sqrt{3}$ , .

3. Найдем периметр треугольника : .

4. Согласно формуле 9.10.1 , найдем площадь боковой поверхности призмы: $LaTeX formula: S_{delta.}=18sqrt[4]{3} cdot 10=180sqrt[4]{3}$ .

Ответ: .

Пример 5. Диагональ прямоугольного параллелепипеда равна см, а диагонали его боковых граней равны см и см. Определите объем параллелепипеда.

Решение. Рассмотрим прямоугольный параллелепипед (рис. 9.50), где , и его измерения; см – диагональ.

Согласно свойству 9.1 . Рассмотрим треугольник . Так как см, то . Рассмотрим треугольник . Так как см, то .

Запишем и решим систему уравнений $LaTeX formula: begin{cases} a^2+b^2+c^2=36, \ b^2+c^2=16, \ a^2+c^2=25 . end{cases}$

Из второго уравнения системы выразим и получим: . Из третьего уравнения выразим и получим: .

Подставим полученные значения и в первое уравнение системы и найдем значение :

, , см.

Зная , определим значения и :

, см; , см.

Согласно формуле 9.2 найдем объем параллелепипеда: ( $LaTeX formula: _{CM}\^3$ ).

Ответ: $LaTeX formula: _{CM}\^3$ .

Пример 6. Определите объем правильной четырехугольной призмы, если ее диагональ образует с плоскостью боковой грани угол $LaTeX formula: 30^{circ}$ , а сторона основания равна .

Решение. Согласно условию задачи основанием призмы является квадрат со стороной (рис. 9.51).

Так как отрезок является проекцией диагонали призмы на грань , то угол является углом наклона диагонали призмы к плоскости боковой грани и $LaTeX formula: angle AB_1D=30^{circ}$ .

Рассмотрим треугольник . По свойству катета лежащего против угла $LaTeX formula: 30^{circ}$ запишем .

Так как согласно свойству 9.1 диагонали прямоугольного параллелепипеда , то , , .

Найдем объем призмы по формуле 9.9 :

Ответ: .

Пример 7. Найдите объем правильной шестиугольной призмы (рис. 9.52), зная, что большая диагональ призмы равна и образует с плоскостью основания призмы угол $LaTeX formula: 30^{circ}$ .

Решение. Рассмотрим большее диагональное сечение призмы и прямоугольный треугольник . Поскольку диагональ призмы и образует с плоскостью основания угол $LaTeX formula: 30^{circ}$ , то катет , лежащий против угла $LaTeX formula: 30^{circ}$ , равен половине гипотенузы, следовательно, высота призмы .

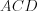
Из теоремы Пифагора: , , .

Так как в основании призмы лежит правильный шестиугольник со стороной , то и $LaTeX formula: a=frac{sqrt{3}}{2}$ .

По формуле $LaTeX formula: S=frac{3sqrt{3}a^2}{2}$ найдем площадь основания призмы: $LaTeX formula: S_{o.}=frac{9sqrt{3}}{8}$ .

По формуле 9.9 найдем объем призмы: $LaTeX formula: V=frac{9sqrt{3}}{8}$ .

Ответ: $LaTeX formula: frac{9sqrt{3}}{8}$ .

1. Треугольная призма не имеет диагоналей.

2. Различайте прямую и наклонную призму: у наклонной призмы – боковые грани параллелограммы, у прямой призмы – боковые грани прямоугольники.

3. Если основание призмы – параллелограмм (ромб, прямоугольник, квадрат), то такую призму называют параллелепипедом. Длины ребер, выходящих из одной вершины параллелепипеда, называют его измерениями.

Источник