Как найти площадь пирамиды в точках abcd

Аналитическая геометрия — задача на расчет пирамиды (тетраэдра)

Краткая теория

Вузовская аналитическая геометрия отличается от курса школьной геометрии. Главное отличие состоит в том, что она основным своим инструментом имеет набор алгебраических формул и методов вычислений. В основе аналитической геометрии лежит метод координат.
Аналитическая геометрия имеет набор формул, готовых уравнений и алгоритмов действия. Для успешного и правильного решения главное — разобраться и уделить задаче достаточно времени.

Данная задача является типовой в курсе аналитической геометрии и требует использования различных методов и знаний, таких как декартовые прямоугольные координаты и вектора в пространстве.

Пример решения задачи

Задача

Даны координаты
вершин пирамиды 
. Найти:

Сделать чертеж.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Длина ребра

Длину ребра

 найдем по
формуле расстояния между 2-мя точками:

Угол между ребрами

Угол между ребрами

 и

 найдем как угол
между направляющими векторами

  и

:

Косинус угла между
векторами:

Угол между ребром и гранью. Векторное произведение

Вычислим угол между
ребром

 и гранью

.

Для этого вычислим
координаты нормального вектора плоскости

 –им будет
векторное произведение векторов 

 и

.

 

Найдем векторное произведение. Для этого

вычислим определитель:

Нормальный вектор
плоскости:

  

Синус угла:

Площадь грани

Вычислим площадь
грани

. Она будет численно равна половине модуля векторного
произведения векторов

    и 

:

Искомая площадь:

Объем пирамиды. Смешанное произведение векторов

Вычислим объем
пирамиды. Он будет равен шестой части модуля смешанного произведения векторов

  и

:

Для того чтобы вычислить смешанное произведение, необходимо
найти определитель квадратной матрицы, составленной из координат векторов:

Искомый объем
пирамиды:

Уравнение прямой в пространстве

Вычислим уравнение
прямой

.  Направляющим
вектором искомой прямой является вектор

. Кроме того, прямая проходит через точку

 

Уравнение искомой
прямой:

Уравнение плоскости

Вычислим уравнение
плоскости

. Нормальный вектор плоскости

. кроме того, плоскость проходит через точку

 -уравнение
грани

 

Уравнение высоты, опущенной на грань

Составим уравнение
высоты, опущенной на грань

 из вершины

:

Нормальный вектор

 является
направляющим вектором высоты, кроме того, высота проходит через точку

 

Искомое уравнение
высоты:

Сделаем схематический чертеж:

Источник

Онлайн решение Пирамиды по координатам вершин

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольной пирамиды (тетраэдра):

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

8) основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Задача 43202 Даны координаты А(0.-1.-1), B(-2.3.5),…

Условие

Даны координаты А(0.-1.-1), B(-2.3.5), С(1.-5,-9), D(-1,-6.3).вершин пирамиды ABCD . Требуется:

а) найти площадь треугольника АВС ;

б) найти объем пирамиды ABCD и длину высоты, опущенную из вершины D на плоскость АВС:

в) записать уравнение плоскости АВС и уравнение высоты, опущенной из вершины D на плоскость АВС.

математика ВУЗ
5047

Все решения

Написать комментарий

Источник

вершины пирамиды в)объем пирамиды ABCD A(3,4,5),B(1,2,1),C(-2,-3,6),D(3,-6,-3) a)ACD б)l=AB,C и D Ответ: a) (√2114), б) (√6174/2)

Дмитрий

18.01.17

Учеба и наука / Математика

1 ответ

Источник

Наш сайт: Fizmathim.ru

Группа ВКонтакте https://vk.com/fizmathim_resh

Перейти на Готовые решения ИДЗ Рябушко (по вариантам)

Решение задач по высшей математике на заказ

ИДЗ 2.2 – Вариант 0

1. Даны векторы a,b и c. Необходимо: а) вычислить смешанное произведение трех векторов; б) найти модуль векторного произведения; в) вычислить скалярное произведение двух векторов; г) проверить, будут ли коллинеарны или ортогональны два вектора; д) проверить, будут ли компланарны три вектора.

1.0 a = 3i – 2j + k, b = 3i – 5j – k, c = 2i + 4j – 3k; а) 2a, –2b, c; б) b, –2c; в) 4a, 2c; г) 2b, c; д) a, –3b, 2c.

а) вычислить смешанное произведение трех векторов 2a, –2b, c;

Так как, то

2a = 6i – 4j + 2k,

–2b = –6i + 10j + 2k, c = 2i + 4j – 3k

Вычисляем по правилу треугольника:

a

11

a12

a13

a

a12a 23a 31 a 21a 32a13 a13a 22a 31 a12a 21a 33 a 23a 32a11

a

21

a 22

a 23

11a 22a 33

a 32

a 33

a 31

Находим смешанное произведение

6

4

2

2a ( 2b) c 6

10

2 6 10 ( 3) ( 4) 2 2 2 ( 6) 4

2

4

3

2 10 2 6 2 4 ( 4) ( 6) ( 3) 180 16 48 40 48 72 260

б) найти модуль векторного произведения b, –2c

Поскольку

b = 3i – 5j – k,

–2c = –4i – 8j + 6k

Векторное произведение a b выражается через координаты данных векторов а и b следующим образом:

i

j

k

y

z

x

z

x

y

a b

x1

y1

z1

1

1

,

1

1

,

1

1

y

z2

x 2

z2

x 2

y2

x 2

y2

z 2

2

Находим векторное произведение

i

j

k

b ( 2c)

3

5

1

( 30 8)i 18 4 j 24 20 k 38i 14 j 44k

4

8

6

модуль векторного произведения :

b ( 2c) 38 2 ( 14)2 ( 44)2 1444 196 1936 3576

в) вычислить скалярное произведение двух векторов 4a, 2c

Находим

4a = 12i – 8j + 4k,

2c = 4i + 8j – 6k

Скалярное произведение двух векторов находим по формуле

a b x1x 2 y1y2 z1z2

Скалярное произведение двух векторов:

4a 2c 12 4 ( 8) 8 4 ( 6) 48 64 24 40

Наш сайт: Fizmathim.ru

Группа ВКонтакте https://vk.com/fizmathim_resh

Перейти на Готовые решения ИДЗ Рябушко (по вариантам)

Решение задач по высшей математике на заказ

г) проверить, будут ли коллинеарны или ортогональны два вектора 2b, c

Так как 2b = 6i – 10j – 2k, c = 2i + 4j – 3k

и

6

10

2

, то векторы 2b и c не коллинеарны,

2

4

3

поскольку

2b c 6 2 ( 10) 4 ( 2) ( 3) 12 40 6 22 0 , то векторы 2b и c неортогональны.

д) проверить, будут ли компланарны три вектора a, –3b, 2c.

Векторы a, b, c компланарны, если abc=0. Вычисляем a = 3i – 2j + k,

–3b = –9i + 15j + 3k, 2c = 4i + 8j – 6k

3

2

1

a ( 3b) 2c 9

15

3

3 15 ( 6) ( 2) 3 4 1 ( 9) 8

4

8

6

1 15 4 3 3 8 ( 2) ( 9) ( 6) 270 24 72 60 72 108 390

т.е. векторы a, –3b, 2c не компланарны.

Наш сайт: Fizmathim.ru

Группа ВКонтакте https://vk.com/fizmathim_resh

Перейти на Готовые решения ИДЗ Рябушко (по вариантам)

Решение задач по высшей математике на заказ

2. Вершины пирамиды находятся в точках A, B, C и D. Вычислить: а) площадь указанной грани; б) площадь сечения, проходящего через середину ребра l и две вершины пирамиды; в) объем пирамиды

ABCD.

2.0 A(2, –3, –1), B(–3, 1, 4), C(3, 2, 5), D(–2, –4, 3); а) ACD; б) l=AB, C и D

а) площадь указанной грани ACD

Известно, что SACD 12 AC AD Находим:

AC 1; 5; 6 AD 4; 1; 4

Векторное произведение a b выражается через координаты данных векторов а и b следующим образом:

i

j

k

y

z

x

z

x

y

a b

x1

y1

z1

1

1

,

1

1

,

1

1

y2

z2

x 2

z2

x 2

y2

x 2

y2

z 2

Вычисляем:

i

j

k

(20 6)i 4 24 j 1 20 k 26i 28j 19k

AC AD

1

5

6

4

1

4

Модуль вектора определяем выражением

a x12 y12 z12

AC AD 262 ( 28)2 192 676 784 361 1821

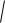
Окончательно имеем:

1

1

SACD

1821

42,67 21,34

2

2

б) площадь сечения, проходящего через середину ребра AB и две вершины пирамиды C и D;

A(2, –3, –1), B(–3, 1, 4), C(3, 2, 5), D(–2, –4, 3);

Находим точку середины ребра BD

x A x B

yA yB

zA zB

2 ( 3)

3 1

1 4

1

3

K

;

;

; K

;

;

; K

; 1;

2

2

2

2

2

2

2

2

7

7

3

3

KC

; 3;

3,5; 3; 3,5

KD

; 3;

1,5; 3; 1,5

2

2

2

2

Площадь сечения находим по формуле:

1

Sceч

KC KD

2

i

j

k

3,5

(4,5 10,5)i 5,25 5,25 j 10,5 4,5 k 15i 10,5j 6k

KC KD

3,5

3

1,5

3

1,5

М одуль равен :

152

( 10,5)2 ( 6)2

KC KD

225 110,25 36 371,25

Sceч

1

19,26

9,63

371,25

2

2

Наш сайт: Fizmathim.ru

Группа ВКонтакте https://vk.com/fizmathim_resh

Перейти на Готовые решения ИДЗ Рябушко (по вариантам)

Решение задач по высшей математике на заказ

в) объем пирамиды ABCD

Поскольку Vпир 16 AB AC AD AB 5; 4; 5

AC 1; 5; 6 AD 4; 1; 4

Находим смешанное произведение векторов:

5

4

5

1

6

5 5 4 4 6 ( 4) 5 1 ( 1) 5 5 ( 4) ( 5) 6 ( 1) 4 1 4

AB

AC

AD

5

4

1

4

100 96 5 100 30 16

147

147

Тогда объем пирамиды ABCD

V

1

147

49

24,5

пир

6

2

Наш сайт: Fizmathim.ru

Группа ВКонтакте https://vk.com/fizmathim_resh

Перейти на Готовые решения ИДЗ Рябушко (по вариантам)

Решение задач по высшей математике на заказ

3. Сила F приложена к точке А. Вычислить: а) работу силы F в случае, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку В; б) модуль момента силы F относительно точки В.

3.0 F = (3, –2, 1), A(3, 3, 2), B(5, 1, –3)

а) работу силы F в случае, когда точка ее приложения, двигаясь прямолинейно, перемещается в точку В;

Так как A F s,

s AB 5 3, 1 3, 3 2 2, 2, 5 , то

A F AB 3 2 ( 2) ( 2) 1 ( 5) 6 4 5 5 A 5

б) модуль момента силы F относительно точки В.

Момент силы M BA F, BA 2, 2, 5

Векторное произведение a b выражается через координаты данных векторов а и b следующим образом:

i

j

k

y

z

x

z

x

y

a b

x1

y1

z1

1

1

,

1

1

,

1

1

y2

z2

x 2

z2

x 2

y2

x 2

y2

z 2

Вычисляем:

i

j

k

(2 10)i 2 15 j 4 6 k 12i 17 j 2k

BA F

2

2

5

3

2

1

Модуль определяем выражением

a 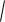x12 y12 z12

Следовательно модуль момента силы F относительно точки В.

M BA F 122 172 ( 2)2 144 289 4 437 20,9

Соседние файлы в предмете Математика

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Понравилась статья? Поделить с друзьями:
  • Как найти длину ребер пирамиды по векторам
  • Как составить рабочий план счетов к учетной политике
  • Победа авиабилеты как найти билет
  • Как найти диаметр окружности через объем
  • Как женщине за сорок найти мужчину