Как найти площадь по клеточкам 1х1 огэ - Исправление недочетов и поиск решений вместе с Examum.ru

Всего: 28 1–20 | 21–28

Добавить в вариант

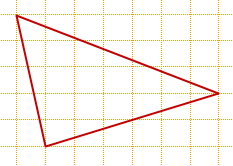
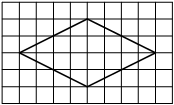
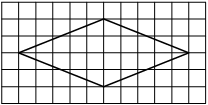
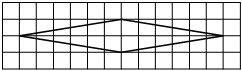
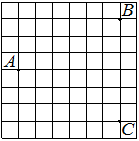
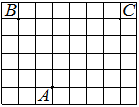
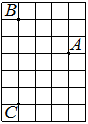
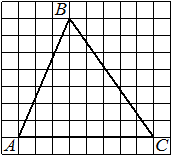
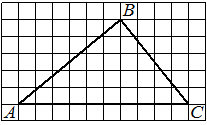
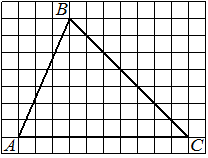
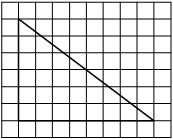
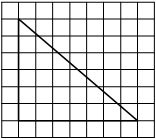
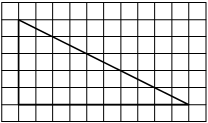
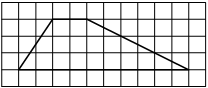
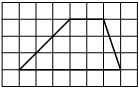
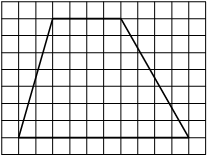
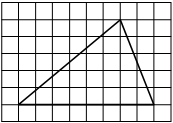
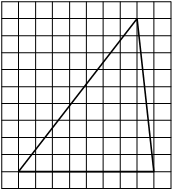
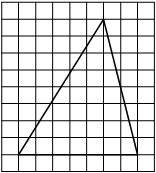
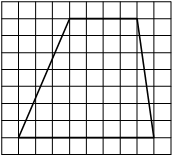
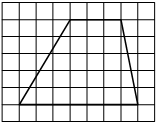
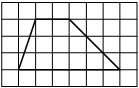
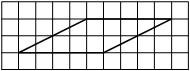
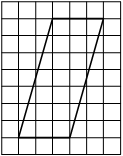
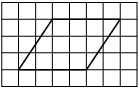
На клетчатой бумаге с размером клетки 1см × 1см изображена трапеция. Найдите её площадь. Ответ дайте в квадратных сантиметрах.

Источник: ГИА-2013. Математика. Диагностическая работа № 2.(1 вар)

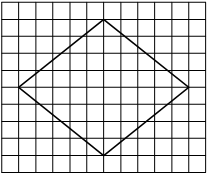
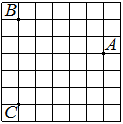
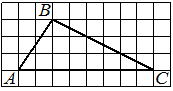
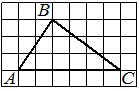
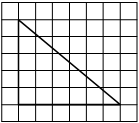
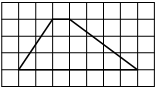
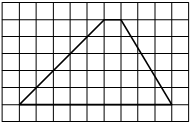
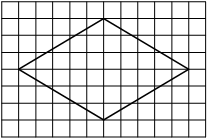
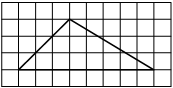
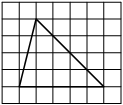
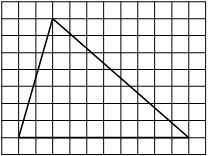
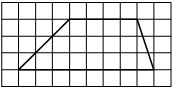
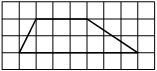
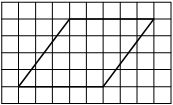
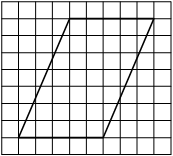
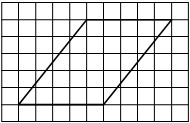
На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

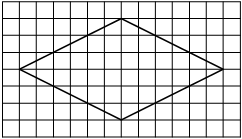
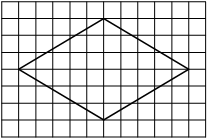
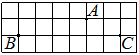
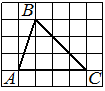
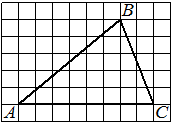
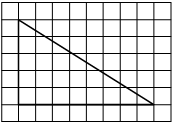
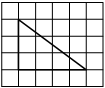
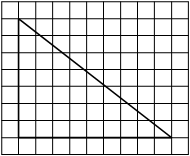
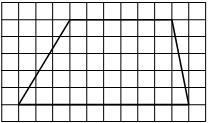
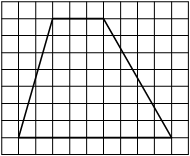
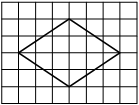
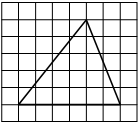
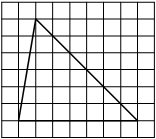
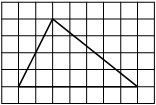
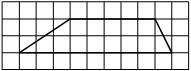
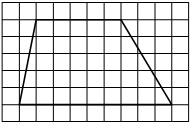
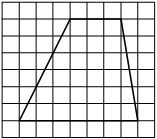
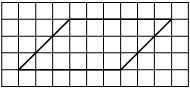
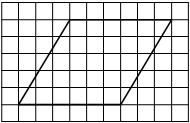
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.

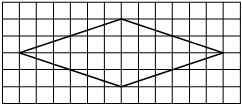
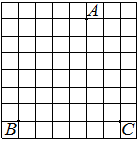
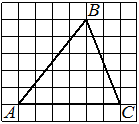
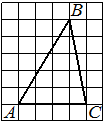
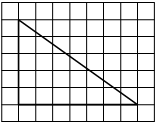
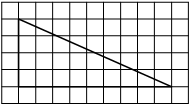
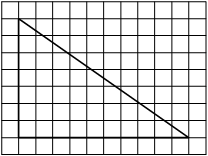
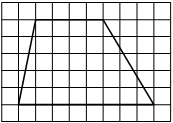
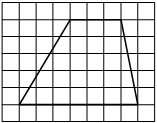
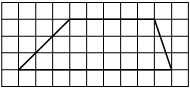
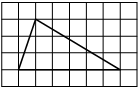
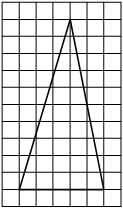
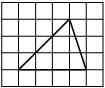
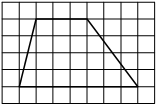
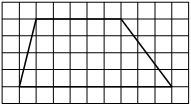
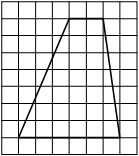
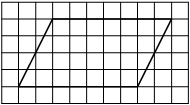
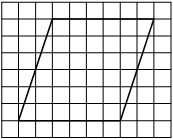
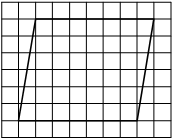
На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.

На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

Источник: Банк заданий ФИПИ

На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

Источник: Банк заданий ФИПИ

На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

Источник: Банк заданий ФИПИ

На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

Источник: Банк заданий ФИПИ

На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.

На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

Источник: Банк заданий ФИПИ

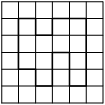
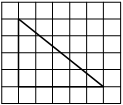
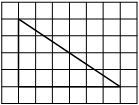
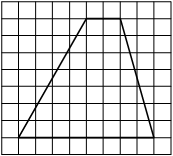
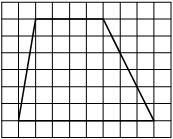
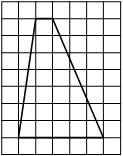
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.

Всего: 28 1–20 | 21–28

Источник

Площадь фигуры (треугольник, четырёхугольник, трапеция и др.) по клеточкам (клеткам).

Какие есть формулы?

Есть способ, при котором надо воспользоваться формулой, основой которой будет понятие узла, узла внутреннего и узла внешнего. Узел это пересечение линий, образующих эти самые клеточки. Внешние узлы, это узлы, находящиеся на сторонах и вершинах геометрических фигур, площади которых нам надо найти. А внутренние узлы, это узлы внутри этих фигур. Клеточки у нас со сторонами равными одному сантиметру (1 см).

Формула, о которой идет речь, называется формула Пика.

Выглядит она вот так:

И по ней очень просто посчитать площадь фигуры S. В этой формуле M это количество внешних узлов, N — количество внутренних узлов.

Приведем пример, возьмем геометрическую фигуру параллелограмм:

Внутренние узлы — синие — N — их у нас 20.

Внешние узлы — красные — М — их у нас 18 и их количество нам надо поделить на два, получится 18/2 = 9 узлов.

Складываем 9 + 20 и вычитаем единицу: 20 + 9 — 1 = 28 см².

Еще один пример:

S = 14/2 + 43 — 1 = 49 см².

система выбрала этот ответ лучшим

Ксарфакс
[156K]

6 лет назад

Допустим, у нас есть произвольная фигура, построенная на листе в клетку. Необходимо вычислить её площадь.

Площадь фигуры по клеточкам

Для того, чтобы найти площадь любой фигуры по клеточкам, можно использовать формулу Пика.

Данная формула основана на подсчёте количества узлов, лежащих внутри фигуры и на её границе.

Узел — это точка, которая лежит на пересечении 2 линий данной сетки: вертикальных и горизонтальных.

Площадь фигуры по клеточкам находится по формуле:

N — количество узлов, которые находятся внутри фигуры.

M — количество узлов, которые находятся на границах (на вершинах и сторонах).

Примеры нахождения площади по клеточкам

1) Найдём площадь треугольника. Будем считать, что одна клетка — это 1 см.

Отметим внутренние узлы и узлы, которые находятся на границах.

N = 7 (внутренние).

M = 8 (узлы на границах).

Площадь треугольника S = 7 + 8/2 — 1 = 10 см².

2) Найдём площадь трапеции по клеточкам, одна клетка — это 1 см. Отметим все узлы и подсчитаем их количество.

N = 11 (внутренние).

M = 12 (узлы на границах).

Площадь трапеции S = 11 + 12/2 — 1 = 16 см².

3) Найдём площадь произвольного многоугольника. Одна клетка — это 1 см.

Отметим внутренние узлы и узлы, расположенные на границах фигуры. Подсчитаем их количество.

N = 6 (внутренние узлы).

M = 8 (узлы на границах).

Площадь многоугольника S = 6 + 10/2 — 1 = 10 см².

Марина Вологда
[295K]

3 года назад

Такие задачи очень часто встречаются, когда известен размер клеточки и дана фигура.

Вот пример таких задач:

Решение зависит от того, какая фигура дана и как именно она размещена относительно клеточек.

Возьмем простой пример, необходимо вычислить площадь вот такого треугольника:

Вспоминаем правило:

Теперь считаем, сколько клеточек треугольник в длину и сколько в высоту. У нас получается 2 в высоту и 6 в длину.

Подставляем к формуле:

S = 1/2 х 2 х 6 = 6 см2.

Считаем по клеточкам, подставляя формулу Пика:

Целых клеточек у нас 3.

Теперь считаем, сколько не целых: 6. Делим их на 2.

S = 3 + 6:2 = 6 см2.

А теперь высчитываем по формуле Пика: количество узлов сетки внутри — 2, количество узлов сетки, лежащих на границах — 10.

Подставляем к формуле и получаем — 2 + 10:2 — 1 = 6 см2.

Теперь давайте рассмотрим вот такой треугольник:

Чтобы найти площадь, вспоминаем правило:

Считаем клеточки и подставляем в формулу:

S = 1/2 х 2 х 6 = 6 см2.

А теперь находим по клеточкам: целых клеточек 2, не целых клеточек 8. Подставляем в формулу: 2 + 8:2 = 6 см2.

Пробуем сделать по формуле Пика: количество узлов сетки внутри — 3, количество узлов сетки, лежащих на границах — 8.

Подставляем к формуле и получаем — 3 + 8:2 — 1 = 6 см2.

Enot-Nina
[110K]

3 года назад

Найти площадь геометрической фигуры можно самыми разными способами:

Самый простой вариант — это вручную посчитать клеточки — целые и половинки также поскладывать. Простой, хотя и не самый быстрый и может не самый точный способ, но он работает. Чтобы легче было считать, достаточно расчертить фигуру на более простые.

Есть еще один способ — это использовать давно разработанную формулу. Это так называемая формула Пика. Для нее нужно посчитать количество узлов — точек пересечения клеточек, что окружены фигурой (находятся внутри нее), а также подсчитать количество пограничных узлов — по контуру фигуры.

Вот на картинке наглядно показано, как ее можно применять, чтоб посчитать площадь любой фигуры по клеточкам:

Бархатные лапки
[382K]

3 года назад

Площадь любого многоугольника можно посчитать по клеточкам. Для этого применяем формулу Пика. На нашем рисунке В — количество узловых клеточек внутри фигуры, Г — количество узлов на границе . Узлы — пересечение двух линий. многоугольника. Площадь равна S = В + Г/2 — 1 Считаем точки на рисунке и подставляем в формулу. — 10 + 7/2 -1 = 12,5.

Таким образом можно посчитать площадь, если вершины фигуры лежат в узлах.

Ann Luka
[2.8K]

6 лет назад

Чтобы найти площадь фигуры по клеточкам, нужно посчитать сколько в фигуре целых клеточек. Потом нужно посчитать сколько не целых и поделить их количество на 2. Добавить к получившемуся числу количество целых клеточек — это и будет правильный ответ.

Например. В треугольнике 3 целых клетки и 4 не целых. 3+4/2=5 пощадь треугольника 5 клеток.

Outline
[18.3K]

3 года назад

Для того, чтобы определить площадь фигуры на бумаге в клеточку есть универсальная формула Пика, позволяющая вычислить площадь изображения, но в только в том случае, если вершины искомой фигуры имеют целые (натуральные числа) координаты. Называется эта формула, в честь Георга Пика:

S=В + Г / 2 − 1

В этой формуле буквенные обозначения означают следующее:

В — количество целочисленных точек внутри многоугольника;

Г — количество целочисленных точек на границе (вершинах и сторонах) многоугольника;

S – площадь фигуры.

Здесь используется понятие «целочисленные» – это те, точки, которые расположены на пересечениях сетки (в ее узлах).

Для примера, найдем площадь треугольника:

Обозначим внутренние точки нашей фигуры красными кружками, а те, что на границах – синим цветом. Считаем красные и синие точки:

В=12, Г=4.

Исходя из подсчетов определяем площадь треугольника по формуле:

S=В+Г/2-1=12+2-1=13.

Можно убедиться в правильность проведенных выше расчетах. Рассчитываем площадь квадрата, обведенного красным, и вычитаем площади зеленого, синего и фиолетового треугольников:

S квадрата равна 36, площади треугольников: синего – 6, зеленого – 2, фиолетового – 15.

Исходя из полученных данных, S белого треугольника равна 13:

S=36-6-15-2=13.

KritikSPb
[93.7K]

3 года назад

Подсчет клеточек — дело полезное. С их помощью можно найти площадь геометрической фигуры.

Достаточно воспользоваться формулой, доказанной Георгом Пиком в 1899 году.

Подходит для расчета площади фигур с прямыми сторонами и целым количеством углов, чаще всего применяют для нахождения площади разносторонних треугольников и многоугольников с числом углов больше 4-х.

На теорему Пика есть задания в ЕГЭ.

127771
[273K]

3 года назад

Сначала я подумал, что нужно будет фигуру, которая указана на рисунке в клеточку разбить по фигурам так, чтобы можно посчитать площадь каждой фигуры по-отдельности, но оказалось все намного проще. Существует для данной задачи специальная формула Пика, которая выглядит следующим образом:

Площадь = В + Г/2 — 1, где:

В — количество целочисленных точек внутри многоугольника.
Г — количество целочисленных точек на границе многоугольника.

Теперь разберемся на примере, у нас есть такой пример:

Перед нами трапеция. Допустим площадь одной клетки 1 кв.см. Теперь можно воспользоваться формулой:

11+12/2-1=16 кв.см.

Бекки Шарп
[71.2K]

3 года назад

Найти площадь фигуры можно если вершины фигуры находятся в уголках клеточек, так называемые Целочисленные вершины или узловые точки. Решать задачу будем по формуле Пика, где

В — количество внутренних узловых точек,
Г — количество граничных узловых точек,

Вот такая фигура у нас —

Считаем точки и подставляем в формулу: S = 17 + 14/2 — 1 = 23

Ответ мы получаем в квадратных единицах, то есть клеточках.

Знаете ответ?

Источник

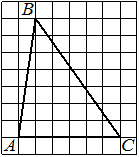
Рассмотрим задачи,в которых требуется найти площадь треугольника изображённого на клетчатой бумаге.

Начнем с прямоугольных треугольников.

Задача 1

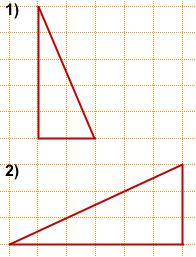
На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник.

Найти его площадь.

Решение:

Площадь прямоугольного треугольника будем искать с помощью формулы

$[S = frac{1}{2}ab,]$

где a и b — катеты.

Длину катетов считаем по клеточкам.

1) a=2, b=5,

$[ S = frac{1}{2} cdot 2 cdot 5 = 5. ]$

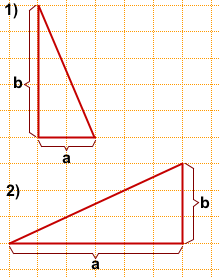
2) a=6, b=3,

$[ S = frac{1}{2} cdot 6 cdot 3 = 9. ]$

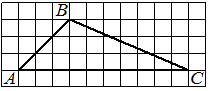
Задача 2

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найти его площадь.

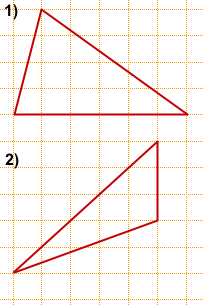
Решение:

Чаще всего площадь произвольного треугольника, изображённого на клетчатой бумаге, ищут по формуле

$[S = frac{1}{2}ah_a ,]$

где a — сторона треугольника, h_a — высота, проведённая к этой стороне.

a и h_a вычисляем по клеточкам (одна из этих величин должна лежать на горизонтальной линии, другая — на вертикальной).

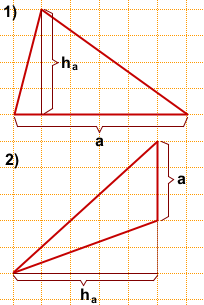
1) a=6, h_a=4,

$[ S = frac{1}{2}ah_a = frac{1}{2} cdot 6 cdot 4 = 12. ]$

2) a=3, h_a=5,

$[ S = frac{1}{2}ah_a = frac{1}{2} cdot 3 cdot 5 = 7,5. ]$

А как найти площадь, если ни одна из сторон треугольника не лежит на горизонтальной или вертикальной линии клеток?

Иногда площадь треугольника можно найти как разность площадей других фигур.

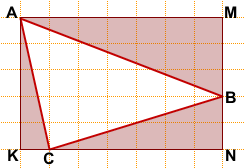
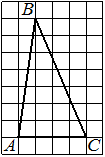
Задача 3

На клетчатой бумаге с размером клетки 1×1 изображён треугольник.

Найдите его площадь.

Решение:

Обозначим вершины треугольника, площадь которого мы ищем, через A, B и C.

Площадь треугольника ABC можно найти как разность площадей прямоугольника AMNK и треугольников AKC, AMB и CBN:

$[S_{Delta ABC} = S_{AMNK} - S_{Delta AKC} - S_{Delta AMB} - S_{Delta CBN} .]$

Площадь прямоугольника найдём по формуле S=ab.

$[ S_{AMNK} = AM cdot AK = 7 cdot 5 = 35. ]$

Площади прямоугольных треугольников найдём по формуле

$[ S = frac{1}{2}ab, ]$

где a и b — катеты.

$[S_{Delta AKC} = frac{1}{2}AK cdot KC = frac{1}{2} cdot 5 cdot 1 = 2,5;]$

$[S_{Delta AMB} = frac{1}{2}AM cdot MB = frac{1}{2} cdot 7 cdot 3 = 10,5;]$

$[S_{Delta CBN} = frac{1}{2}CN cdot BN = frac{1}{2} cdot 6 cdot 2 = 6.]$

Отсюда

$[S_{Delta ABC} = 35 - 2,5 - 10,5 - 6 = 16.]$

Источник

Это задание из ОГЭ по математике предлагает найти площади, углы, длины геометрических фигур, нарисованных на фоне в клетку. Задание 18 с кратким ответом, в ответ идет только число.

Реальные задания №18 по геометрии из банка ФИПИ

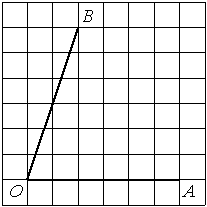
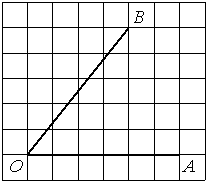
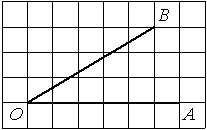
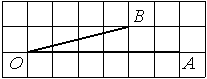
Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=6/2=3.
Ответ: 3

AE8B22

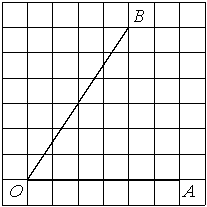
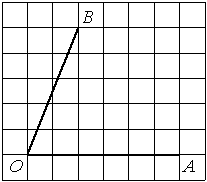
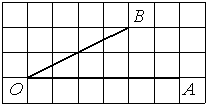
Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=6/4=1,5.
Ответ: 1,5

09C3B1

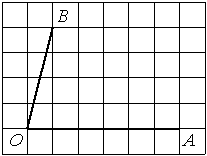
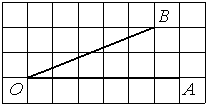
Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=5/4=1,25.
Ответ: 1,25

739060

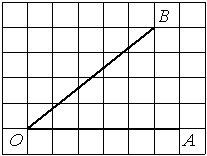
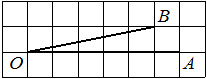
Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=5/2=2,5.
Ответ: 2,5

0747AA

Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=4/1=4.
Ответ: 4

9C09A9

Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=4/5=0,8.
Ответ: 0,8

A1ECAA

Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=3/5=0,6.
Ответ: 0,6

887E42

Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=2/4=0,5.
Ответ: 0,5

201054

Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=2/5=0,4.
Ответ: 0,4

E73651

Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=1/5=0,2.
Ответ: 0,2

A601D0

Найдите тангенс угла AOB, изображённого на рисунке.

Решение:

Опустим перпендикуляр из точки B на прямую AO для получения прямоугольного треугольника. Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему: tgAOB=1/4=0,25.
Ответ: 0,25

51BEC9

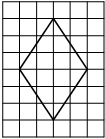
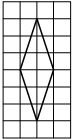
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 6*4=12
Ответ: 12

F519DD

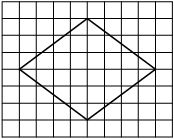
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 10*2=10
Ответ: 10

704DB1

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 6*8=24
Ответ: 24

2F4DA5

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 6*2=6
Ответ: 6

1F239C

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 8 * 4 = 16
Ответ: 16

33E327

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 12 * 6 = 36
Ответ: 36

0B92D0

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 8 * 2 = 8
Ответ: 8

3B5D8B

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 10 * 4 = 20
Ответ: 20

CFCA33

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 10 * 8 = 40
Ответ: 40

3B008A

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 10 * 6 = 30
Ответ: 30

8372E0

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 12 * 4 = 24
Ответ: 24

FFD1EE

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите площадь этого ромба.

Решение:

Площадь ромба равна половине произведения диагоналей. 1/2 * 12 * 2 = 12
Ответ: 12

E2A932

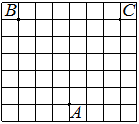
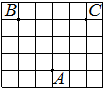
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до середины отрезка BC.

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 3

969F4E

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 5

AFB9A1

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 1

D234F7

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 2

68F679

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 4

9672D7

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 5

3F311F

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 6

C598DA

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 8

FCC29D

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 7

0DBF9B

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 6

B73FA9

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 1

78BDFE

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 7

CB1715

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 3

107F53

Решение:

Находим середину ВС, проводим к ней прямую от точки А, считаем клетки.
Ответ: 2

5B4C37

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 4

FEDC09

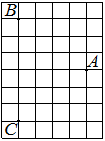
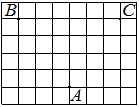
На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 6

C563EA

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 5

B2853A

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 4

FE13B1

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 2

C8BF73

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 5

A4B62F

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 2

DA3762

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 7

C576A6

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 1

9D880E

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 4

078B48

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 6

854014

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 3

B4DCCF

На клетчатой бумаге с размером клетки 1×1 отмечены три точки: A, B и C. Найдите расстояние от точки A до прямой BC.

Решение:

Проводим перпендикуляр от точки А к ВС, считаем клетки.
Ответ: 8

259D23

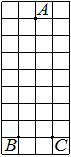
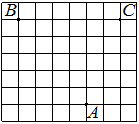
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

Решение:

Из рисунка видно, что длина стороны AC равна 6. Длина средней линии равна половине длины стороны AC, следовательно, 3.
Ответ: 3

9C2804

Решение:

Из рисунка видно, что длина стороны AC равна 10. Длина средней линии равна половине длины стороны AC, следовательно, 5.
Ответ: 5

BC4EBE

Решение:

Из рисунка видно, что длина стороны AC равна 4. Длина средней линии равна половине длины стороны AC, следовательно, 2.
Ответ: 2

7ECBCE

Решение:

Из рисунка видно, что длина стороны AC равна 8. Длина средней линии равна половине длины стороны AC, следовательно, 4.
Ответ: 4

D2D94B

Решение:

Из рисунка видно, что длина стороны AC равна 8. Длина средней линии равна половине длины стороны AC, следовательно, 4.
Ответ: 4

8F5C52

Решение:

Из рисунка видно, что длина стороны AC равна 4. Длина средней линии равна половине длины стороны AC, следовательно, 2.
Ответ: 2

686EFB

Решение:

Из рисунка видно, что длина стороны AC равна 6. Длина средней линии равна половине длины стороны AC, следовательно, 3.
Ответ: 3

07C968

Решение:

Из рисунка видно, что длина стороны AC равна 10. Длина средней линии равна половине длины стороны AC, следовательно, 5.
Ответ: 5

E3456A

Решение:

Из рисунка видно, что длина стороны AC равна 6. Длина средней линии равна половине длины стороны AC, следовательно, 3.
Ответ: 3

794271

Решение:

Из рисунка видно, что длина стороны AC равна 8. Длина средней линии равна половине длины стороны AC, следовательно, 4.
Ответ: 4

A1906B

Решение:

Из рисунка видно, что длина стороны AC равна 4. Длина средней линии равна половине длины стороны AC, следовательно, 2.
Ответ: 2

E52B99

Решение:

Из рисунка видно, что длина стороны AC равна 10. Длина средней линии равна половине длины стороны AC, следовательно, 5.
Ответ: 5

E331C7

На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 6

F7FF65

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 8

AAC1BC

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 7

2BD44A

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 8

6DE9A6

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 4

39A91A

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 9

197283

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 5

2EA9C2

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 7

ED1F0E

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 9

10323E

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 10

ED4E1A

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 6

4FAEEC

Решение:

Катет — сторона, прилежащая к прямому углу. Посчитаем клетки в большем катете.
Ответ: 10

F8232E

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (1+7) : 2 = 4
Ответ: 4

351A72

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (6+10) : 2 = 8
Ответ: 8

5EFE19

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (4+8) : 2 = 6
Ответ: 6

C05266

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (2+10) : 2 = 6
Ответ: 6

CFD6D8

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (3+7) : 2 = 5
Ответ: 5

3BD771

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (2+8) : 2 = 5
Ответ: 5

869450

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (1+5) : 2 = 3
Ответ: 3

19D522

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (2+6) : 2 = 4
Ответ: 4

A28F9D

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (1+9) : 2 = 5
Ответ: 5

2EF821

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (3+9) : 2 = 6
Ответ: 6

45A5FF

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (5+9) : 2 = 7
Ответ: 7

7AAADC

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину её средней линии.

Решение:

Длина средней линии трапеции равна полусумме её оснований, т. е. (4+10) : 2 = 7
Ответ: 7

321F00

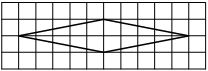
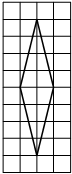
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10

87C214

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 6

6CB64A

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 8

4801B0

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 12

DEA70E

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 8

6D0D8F

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 12

8D9098

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 8

90A16B

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10

F3D7EA

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10

35106F

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 10

1C594B

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 6

E4F439

На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите длину его большей диагонали.

Решение:

Диагональ — прямая линия, соединяющая вершины двух углов, не прилежащих к одной стороне. Находим большую. Считаем клеточки.
Ответ: 12

657F97

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 6 * 3 = 9
Ответ: 9

E873D3

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 8 * 5 = 20
Ответ: 20

9E69AF

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 8 * 3 = 12
Ответ: 12

53C928

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 6 * 5 = 15
Ответ: 15

EE2C25

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 5 * 10 = 25
Ответ: 25

1B4EAF

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 8 * 9 = 36
Ответ: 36

94B40E

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 5 * 4 = 10
Ответ: 10

F50FF8

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 7 * 6 = 21
Ответ: 21

3A7F81

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 4 * 3 = 6
Ответ: 6

DFB4EA

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 7 * 8 = 28
Ответ: 28

7AEBD7

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 10 * 7 = 35
Ответ: 35

4718F7

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Решение:

Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию
S = 1/2 * 7 * 2 = 14
Ответ: 14

0C5645

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (7+3) * 4= 20
Ответ: 20

695D77

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (4+8) * 7= 42
Ответ: 42

07B1AD

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (4+8) * 3 = 18
Ответ: 18

4774FE

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (5+9) * 2= 14
Ответ: 14

284762

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (5+9) * 4= 28
Ответ: 28

2916B2

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (3+7) * 5= 25
Ответ: 25

867701

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (5+9) * 5= 35
Ответ: 35

B5D99F

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (2+6) * 7= 28
Ответ: 28

B11571

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (4+8) * 6= 36
Ответ: 36

E46263

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (2+6) * 3= 12
Ответ: 12

283DE4

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (3+7) * 2= 10
Ответ: 10

383C46

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:

Площадь трапеции равна произведению полусуммы оснований на высоту
S = 1/2 * (3+7) * 6= 30
Ответ: 30

2E7B84

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 7 * 4 = 28
Ответ: 28

71E23E

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 2 = 10
Ответ: 10

3BD9B6

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 4 = 20
Ответ: 20

5C5046

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 6 * 3 = 18
Ответ: 18

566A4E

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 6 * 6 = 36
Ответ: 36

0275CC

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 3 * 7 = 21
Ответ: 21

E81F8D

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 7 = 35
Ответ: 35

2A59D7

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 7 * 2 = 14
Ответ: 14

5FC71A

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 6 * 5 = 30
Ответ: 30

257B6F

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 7 * 6 = 42
Ответ: 42

839354

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 4 * 3 = 12
Ответ: 12

C1A1AF

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Решение:

Площадь параллелограмма равна произведению основания на проведенную к нему высоту
S = 5 * 5 = 25
Ответ: 25

9B4AE0

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 14

11403B

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 8

CDF457

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 15

06B968

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 10

AFB70E

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 13

C4025D

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 16

E4CBB2

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 9

211628

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 17

5D3FCF

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 19

320729

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 18

C72856

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 12

BB2950

На клетчатой бумаге с размером клетки 1×1 изображена фигура. Найдите её площадь.

Решение:

Считаем клетки внутри фигуры.
Ответ: 11

F78C61

Источник

Рассмотрим несколько задач.

Задача #1

(Номер задачи на fipi.ru — B11571). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Прежде чем приступать к решению задачи, вспомним теорию >>

Трапеция — четырёхугольник, две стороны которой параллелльны, а две другие нет. Параллельные стороны называются основаниями, а непаралельные — боковыми.

Площадь трапеции вычисляется по формуле:

$[S=frac{a+b}{2}cdot h]$

где a и b — основания трапеции, h — высота трапеции.

Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 2, b = 6. Из рисунка также находим высоту трапеции: h = 7.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:

$[S=frac{2+6}{2}cdot 7 = 28]$

Ответ: площадь трапеции равна: 28 ед. кв.

Задача #2

(Номер задачи на fipi.ru — E46263). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 4, b = 8. Из рисунка также находим высоту трапеции: h = 6.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:

$[S=frac{4+8}{2}cdot 6 = 36]$

Ответ: площадь трапеции равна: 36 ед. кв.

Задача #3

(Номер задачи на fipi.ru — 283DE4). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 2, b = 6. Из рисунка также находим высоту трапеции: h = 3.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:

$[S=frac{2+6}{2}cdot 3 = 12]$

Ответ: площадь трапеции равна: 12 ед. кв.

Задача #4

(Номер задачи на fipi.ru — 383C46). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 3, b = 7. Из рисунка также находим высоту трапеции: h = 2.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:

$[S=frac{3+7}{2}cdot 2 = 10]$

Ответ: площадь трапеции равна: 10 ед. кв.

Задача #5

(Номер задачи на fipi.ru — 2E7B84). На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

Решение:
Посмотрим на рисунок. Из него видно, что основания трапеции равны соответственно: a = 3, b = 7. Из рисунка также находим высоту трапеции: h = 6.

Таким образом, осталось подставить все найденный значения в формулу и найти площадь трапеции:

$[S=frac{3+7}{2}cdot 6 = 30]$

Ответ: площадь трапеции равна: 30 ед. кв.

Источник