Математика, 3 класс
Урок №22. Площадь прямоугольника
Перечень вопросов, рассматриваемых в теме:
- Как вычислить площадь прямоугольника?
- В каких единицах измеряется площадь?
- Какими способами можно сравнить геометрические фигуры?
Глоссарий по теме:
Площадь – внутренняя часть любой плоской геометрической фигуры.
Квадрат – это прямоугольник, у которого все стороны равны.
Прямоугольник – это четырёхугольник, у которого все углы прямые.
Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Основная и дополнительная литература по теме урока:
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 60-61.
2. Рудницкая В. Н. Тесты по математике:3 класс. М.: Издательство «Экзамен», 2016 с. 38-43.
3. Волкова Е. В. ВПР. Математика 3 класс Практикум по выполнению типовых заданий. ФГОС .М.: Издательство «Экзамен», 2018, с. 36-53.
Теоретический материал для самостоятельного изучения
Упоминание о первых геометрических фигурах встречается еще у древних египтян и древних шумеров. Учёными-археологами (они ищут разные исторические древности) был найден папирусный свиток (бумага древних египтян, изготавливаемая из растения папирус) с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом. Одним определенным словом называлась фигура прямоугольник независимо от того какие стороны были у этого прямоугольника. А если у прямоугольника все стороны были одинаковые, то такой прямоугольник имел специальное название – квадрат. Таким образом, значит, что уже в те далекие времена люди имели представление о геометрии и знали изучаемые этой наукой фигуры. Название «геометрическая фигура» придумали древние греки. И названия всем геометрическим фигурам дали тоже древнегреческие учёные.
Найдём площадь геометрической фигуры.
Чтобы найти площадь фигуры, надо узнать сколько раз в фигуре поместится квадрат со стороной 1 см. Площадь этой геометрической фигуры составляет 18 квадратов. Для удобства подсчёта количество квадратов можно воспользоваться знаниями таблицы умножения. По 6 взять 3 раза получится 18 квадратов.
Найдём площадь прямоугольника со сторонами 6 см и 3 см.
Для этого достаточно умножить длину на ширину. 6 ∙ 3 = 18 см2
Таким образом, формулируем вывод: чтобы найти площадь прямоугольника, надо длину умножить на ширину.
S = a ∙ b
S – площадь
a – длина
b – ширина
Задания тренировочного модуля:
1. Заполните пропуски в таблице.
|
а |
5 |
6 |
3 |
|
|
b |
8 |
9 |
||
|
S |
15 |
56 |
24 |
Правильный ответ:
|
а |
5 |
7 |
6 |
3 |
|
b |
3 |
8 |
9 |
8 |
|
S |
15 |
56 |
54 |
24 |
2. Длина прямоугольника 8см, ширина 4 см. Чему равна площадь прямоугольника? Выделите правильный ответ.
12 см; 32 см; 24 см2; 32 см2; 24; 12 см2.
Правильный ответ: 32см2.
Периметр данного многоугольника можно найти сложив длинны всех его сторон, но для начала придётся найти длинны двух сторон — АВ и АК:
АВ = CD + EK = 2 + 1 = 3 см
AK = BC + DE = 4 + 2 = 6 см
Теперь можно найти периметр всей фигуры:
Р = AB + BC + CD + DE + EK + AK = 3 + 4 + 2 + 2 + 1 + 6 = 18 см
Площадь же многоугольника можно найти, как минимум пятью способами ( правда не уверен, что в третьем классе уже умеют находить площадь трапеций по длинам оснований и высоте — в данном случае трапеции ABCD и ADEK ). Для того, чтобы проще описать способы решения я добавил на чертёж ещё три точки ( впрочем, для разных вариантов решения не все точки потребуются одновременно ).
Вот такой чертёжик у меня получился
Проще всего найти площадь этой фигуры так
S = S(ABEK) — S(CDEH) = AB * AK — CD * DE = 3 * 6 — 2 * 2 = 18 — 4 = 14 см²
Второй способ:
S = S(ABCG) + S(DEGK) = AB * BC + DE * EK = 3 * 4 + 2 * 1 = 12 + 2 = 14 см²
Третий способ:
S = S(BCDF) + S(AFEK) = BC * CD + AK * EK = 4 * 2 + 6 * 1 = 8 + 6 = 14 см²
Четвёртый способ:
S = S(BCDF) + S(AFDG) + S(DEKG) = BC * CD + AG * AF + DE * EK = 4 * 2 + 4 * 1 + 2 * 1 = 8 + 4 + 2 = 14 см²
Ну, и, наконец, пятый способ с трапециями ( извиняюсь, забыл провести на чертеже ещё и AD, впрочем в решении его величина не важна ):
S = S(ABCD) + S(ADEK) = BC * ( AB + CD )/2 + EK * ( DE + AK )/2 = 4 * ( 3 + 2 )/2 + 1 * ( 2 + 6 )/2 = 10 + 4 = 14 см²
Ответ: периметр многоугольника равен 18 см, а его площадь — 14 см²
- Главная
- Справочники
- Справочник по математике для начальной школы
- Основы геометрии
- Площадь фигуры
В этом разделе мы познакомимся с новым математическим понятием: с площадью фигуры.
Площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией
Ты знаешь другие понятия, которые тоже называют словом ПЛОЩАДЬ.
Например, площадь в городе — это чаще всего красивое место с клумбами, фонтаном и памятниками.
Посевная площадь — это участок земли, предназначенный для сельскохозяйственных целей.
Сравнение площадей фигур
При сравнении площади фигур, мы узнаём, больше или меньше места занимает данная фигура на плоскости.
Например, сравним площади двух фигур: треугольника и круга.
Мы видим, что площадь треугольника больше площади круга. Это видно на глаз, то есть первый способ сравнения площадей фигур: на глазок.
Сравнение площадей способом наложения
Иногда на глаз трудно определить, площадь какой фигуры больше. Давай сравним площади двух треугольников:
Совместим фигуры так, чтобы одна фигура полностью поместилась в другой.
Мы видим, что синий треугольник поместился в красном треугольнике, значит, площадь красного треугольника больше, чем площадь синего треугольника.
Сравнение площадей заданной меркой
Иногда нельзя определить, площадь какой фигуры больше способом наложения. Давай сравним площади двух фигур:
В таком случае измерять площади фигур будем заданной меркой, а потом сравним их.
Например, меркой может быть вот такой прямоугольник :
В первой фигуре поместилось 5 мерок, во второй фигуре поместилось 5 таких же мерок. Значит, площади фигур равны.
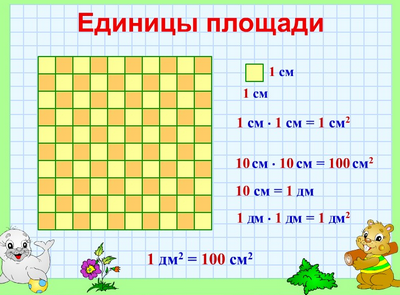
Единицы площади
В математике измерять площади фигур математики всего мира договорились одинаковыми мерками.
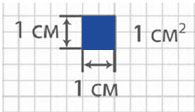
Квадратный сантиметр
Квадрат, сторона которого 1 см – это единица площади – квадратный сантиметр: см²
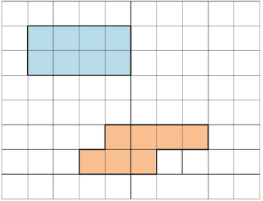
Определим площадь данных фигур:
В синей фигуре 8 см², а в красной фигуре – 7 см².
8 > 7, значит, 8 см² > 7 см² а это значит, что площадь синей фигуры больше, чем площадь красной фигуры.
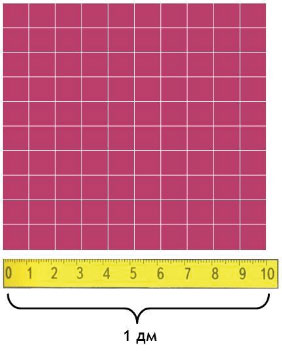
Квадратный дециметр
Квадрат, сторона которого 1 дм – это единица площади – квадратный дециметр: дм²
Вычислим, сколько квадратных сантиметров содержится в 1 квадратном дециметре:
1 дм² = ? см²
Сторона такого квадрата равна 10 см, а площадь квадрата равна произведению его сторон, то есть
10 • 10 = 100 см²
Значит, 1 дм² = 100 см²
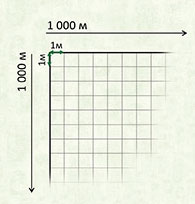
Квадратный метр
Квадрат, сторона которого 1 м – это единица площади – квадратный метр: м²
Этой единицей мы пользуемся, когда хотим узнать площадь комнаты, класса, школьного двора или бабушкиного сада.
1 м² = 100 дм²
Квадратный километр
Квадрат, сторона которого 1 км – это единица площади – квадратный километр: км²
Этой единицей мы пользуемся, когда хотим узнать площадь города или страны. Например, площадь России составляет более семнадцати миллионов квадратных километров.
1 км² = 1000000 м²
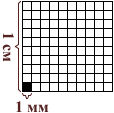
Квадратный миллиметр
Квадрат, сторона которого 1 мм – это единица площади – квадратный миллиметр: мм²
Этой единицей мы пользуемся для измерения очень маленьких площадей.
1 см² = 100 мм²
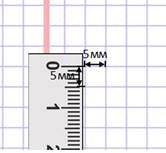
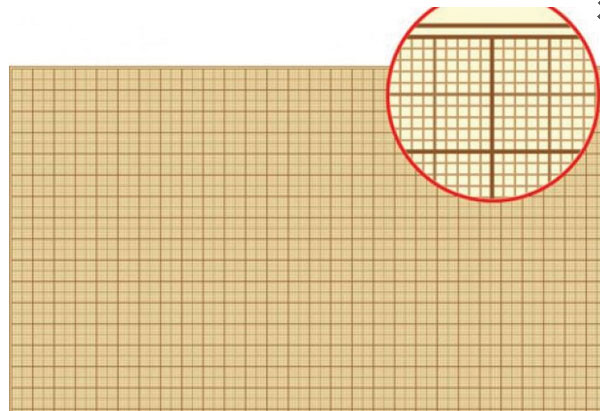
Длина и ширина клеточки школьной тетради по математике – пять миллиметров, значит там пять рядов по пять квадратных миллиметров. 5 • 5 = 25, поэтому в одной клеточке двадцать пять квадратных миллиметров.
Для черчения и измерения фигур маленькой площади удобно использовать миллиметровую бумагу.
Ар
Ар — это площадь квадрата со стороной 10 м.
Слово «ар» при числах сокращённо записывают так:
1 а, 20 а, 97 а.
1 а2 = 100 м2, поэтому ар часто называют соткой.
Гектар
Гектар — это площадь квадрата со стороной 100 м.
Слово «гектар» при числах сокращённо записывают так:
1 га, 20 га, 530 га.
Чтобы перевести площадь из квадратных метров в гектары, необходимо число квадратных метров разделить на 10000.
Ар и гектар используются при измерении земельных участков.
Советуем посмотреть:
Площадь прямоугольника
Круг. Шар. Овал
Треугольники
Многоугольники
Угол. Виды углов
Обозначение геометрических фигур буквами
Периметр многоугольника
Окружность
Основы геометрии
Правило встречается в следующих упражнениях:
2 класс
Страница 40. Урок 16,
Петерсон, Учебник, часть 2
Страница 45. Урок 17,
Петерсон, Учебник, часть 2
Страница 50. Урок 19,
Петерсон, Учебник, часть 2
Страница 58. Урок 23,
Петерсон, Учебник, часть 2
Страница 61. Урок 24,
Петерсон, Учебник, часть 2
Страница 79. Урок 32,
Петерсон, Учебник, часть 2
Страница 81. Урок 33,
Петерсон, Учебник, часть 2
Страница 82. Урок 34,
Петерсон, Учебник, часть 2
Страница 91. Урок 38,
Петерсон, Учебник, часть 2
Страница 56. Урок 20,
Петерсон, Учебник, часть 3
3 класс
Страница 59,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 71,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 72. ПР 1. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 25,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 54,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 10. Урок 3,
Петерсон, Учебник, часть 1
Страница 22. Урок 7,
Петерсон, Учебник, часть 1
Страница 39. Урок 15,
Петерсон, Учебник, часть 2
Страница 42. Урок 19,
Петерсон, Учебник, часть 3
Страница 75. Повторение,
Петерсон, Учебник, часть 3
4 класс
Страница 70,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 34,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 32. Тест 1. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 53. Тест 2. Вариант 2,
Моро, Волкова, Проверочные работы
Страница 6,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 17,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 61,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 76,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 66,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 3. Урок 1,
Петерсон, Учебник, часть 1
Чтобы сравнить площади фигур, можно фигуры наложить друг на друга.
Пример:
Внутри квадрата полностью поместился круг.
Можно сделать вывод, что площадь круга меньше, чем площадь квадрата. И наоборот, площадь квадрата больше площади круга.
Для сравнения данных фигур можно подсчитать квадраты с одинаковой площадью, на которые разбита каждая фигура, и сравнить полученные числа.
Пример:
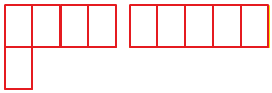
первая фигура состоит из (6) квадратов, а вторая фигура состоит из (9) таких же квадратов.
Значит, площадь первой фигуры меньше, чем площадь второй фигуры.
Определим площадь прямоугольника со сторонами (2) см и (4) см.
Фигура составлена из (8) квадратов площадью (1) см(²).
Чтобы найти площадь прямоугольника, надо найти произведение длин его сторон.
2 см⋅4 см=8 см2
.
Длина и ширина прямоугольника должны быть выражены (записаны) в одинаковых единицах длины.
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а
Периметр – сумма длин всех сторон фигуры.
Нахождение периметра
Р ф. = а + b + c + …
Р пр. = (а + b) · 2
Р кв. = а · 4
Чтобы найти площадь фигуры, надо длину умножить на ширину.
Нахождение площади
S пр. = а · b
S кв. = а · а