Как найти площадь по теореме пика - Исправление недочетов и поиск решений вместе с Examum.ru

Каждому из нас нередко приходилось считать площадь решётчатого многоугольника (изображённого, например, на клетчатой бумаге). В основном, это делают ещё по известным со школы формулам. Но в этом случае для каждой фигуры приходится помнить выражение её площади.
Не легче ли использовать одну формулу для всех многоугольников?
— Сказка? — Нет, теорема Пика!

• Названа она в честь Георга Пика (нет, не оружия или покемона), доказавшего её в 1899 году.

Формулировка звучит так:
S = В + Г / 2 − 1, где S — площадь многоугольника, В — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
• Важное замечание: формула справедлива только для многоугольников, у которых вершины расположены в узлах решетки.

Например, для многоугольника на рисунке, В=7 (красные точки), Г=8 (зелёные точки), поэтому S = 7 + 8/2 — 1 = 10 квадратных единиц.

Докажем теорему Пика:
• Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки. Пусть длины его сторон равны a и b. Имеем в этом случае В = (a-1)(b-1), Г = 2a+2b и, по формуле Пика, S = (a-1)(b-1)+a+b-1 = ab .
• Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами a и b, рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат c целочисленных точек. Тогда для этого случая В = ((a-1)(b-1)-c+2)/2, Г = (2a+2b)/2+c-1 и получаем, что S = ab/2.
• Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников (см. рисунок). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.

• Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой многоугольник можно триангулировать, т.е. разбить на треугольники (например, диагоналями). Отсюда по индукции следует, что формула Пика верна для любого многоугольника. чтд

К сожалению, эта столь простая и красивая формула плохо обобщается на высшие размерности.
Наглядно показал это Рив, предложив в 1957 г. рассмотреть тетраэдр (называемый теперь тетраэдром Рива) со следующими вершинами:
A(0,0,0), B(1,0,0), C(0,1,0), D(1,1,k)
Тогда этот тетраэдр ABCD при любых k не содержит внутри ни одной точки с целочисленными координатами, а на его границе — лежат только четыре точки A, B, C, D. Таким образом, объём и площадь поверхности этого тетраэдра могут быть разными, в то время как число точек внутри и на границе — неизменны; следовательно, формула Пика не допускает обобщений даже на трёхмерный случай.
Тем не менее, некоторое подобное обобщение на пространства большей размерности всё же имеется, — это многочлены Эрхарта, но они весьма сложны, и зависят не только от числа точек внутри и на границе фигуры.

Специально для ЖЖ матфака, Сергей Романов.

Источник

Вокруг формулы Пика

Уровень сложности
Средний

Время на прочтение
2 мин

Количество просмотров 2.3K

Как найти площадь произвольного многоугольника с вершинами в узлах клетчатой бумаги?

В простых ситуациях его можно разбить на треугольники (рис. 1а) или, наоборот, достроить до прямоугольника (рис. 1б). Но как быть в общем случае? Посмотрите, скажем, на рисунок 1в.

Оказывается, достаточно подсчитать числовершин внутри многоугольника и число на его границе — тогда его площадьбудет равна

$S = I + frac B 2 − 1.$

Это формула называется формулой Пика в честь австрийского математика Георга Пика (1859–1942), открывшего её в 1899 году. Так, для многоугольника на рисунке 1в имеем

, , поэтому $S = 13 + frac {20} {2} − 1 = 22.$

Формула выглядит удивительно просто. Интересно, столь же просто её доказать?

Этап 1: ШАГ ИНДУКЦИИ. Предположим, что многоугольник разбит диагональю на два, для которых формула доказана. Тогда несложно показать, что она верна и для.

Этап 2: ТРИАНГУЛЯЦИЯ. Многократно проводя внутренние диагонали, разобьём наш многоугольник на элементарные треугольники (не содержащие узлов ни на границе, ни внутри, кроме вершин). Для такого треугольникаипоэтому площадь должна быть равна

Этап 3: БАЗА ИНДУКЦИИ. Остаётся доказать, что площадь элементарного треугольника равнаМы приведём важное и красивое рассуждение.

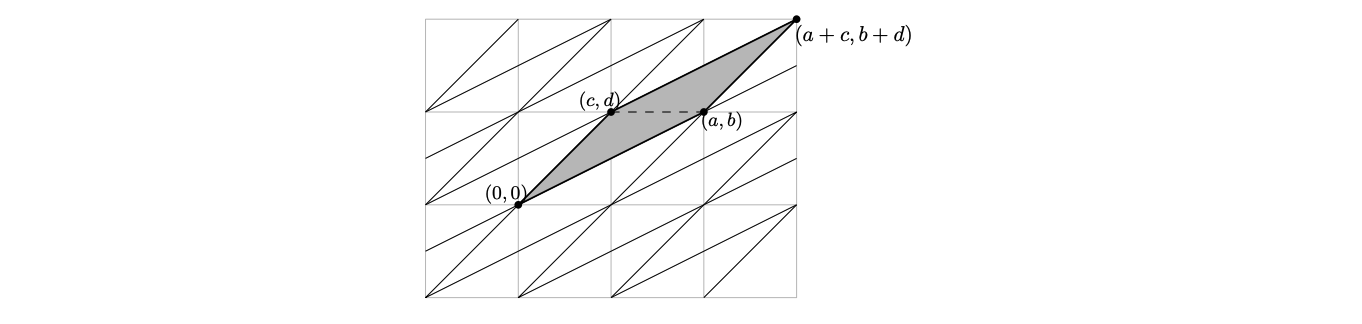
Пусть треугольник имеет вершины иДостроим его до параллелограмма, добавив вершину и замостим его копиями всю плоскость (рис. 2).

Элементарность нашего треугольника равносильна тому, что любой узелможно получить из узлацелочисленными сдвигами сторониИными словами, для любых целыхинайдутся целыеитакие, что

$x(a, b) + y(c, d) = (e, f) Longleftrightarrow begin{cases} ax + cy = e \ bx + dy = f. end{cases}$

Неожиданно, геометрическая задача свелась к чисто алгебраической — системе линейных уравнений. Её решение даётся формулами Крамера

$x = frac {de − cf} ∆ , ;; y = frac {af − be} ∆ , ;;где ;; ∆ = ad − bc ;; — ;; textit {определитель} ;;системы .$

Хорошо известно, что определительпо модулю равен площади параллелограмма, построенного на векторахипоэтому нам надо доказать, что
Приимеема при
Так каквсегда должны быть целыми, то кратныоткудакратно , что возможно, лишь при Формула Пика доказана.

В заключение сделаем несколько замечаний.

Приведённое рассуждение с замещением плоскости на школьном языке иллюстрирует важные идеи высшей алгебры — описание базисов свободной абелевой группыи группы её автоморфизмов:

$Aut(mathbb Z^2) ; cong ; GL_2 (mathbb Z)=left{begin{pmatrix} a & b \ c & d end{pmatrix} middle| ad-bc=pm 1 right}.$
Последний факт можно обобщить на высшие размерности: $Aut(mathbb Z^n) ; cong ; { {A| det ;A = ±1} }.$
А вот формула Пика неверна уже в трёхмерном пространстве: объём многогранника с целыми вершинами не выражается через количества вершин внутри, на гранях и рёбрах.
Вместе с тем существуют варианты обобщения формулы Пика для некоторых классов целочисленных многомерных многогранников (например, с центрально-симметричными гранями).

Автор: Андрей Канунников, к. ф.-м. н., мехмат МГУ, преподаватель ШАД Хелпер

Источник

Игорь Акулич
«Квантик» №8, 2021

Знаменитая формула Пика получила своё название по имени автора — австрийского учёного Георга Александра Пика, опубликовавшего её на рубеже XIX и XX веков. Формула Пика удивительно красива, и потому является любимой темой популярных публикаций (можно порекомендовать статью Г. Мерзона «Площадь многоугольников и тающий лед» из 9-го номера «Квантика» за 2018 год либо более раннюю статью Н. Васильева «Вокруг формулы Пика» из 12-го номера «Кванта» за 1974 год — в этих статьях приводится и её доказательство).

Поскольку, возможно, не все читатели в курсе дела, вкратце изложим суть. Пусть бесконечная плоскость разбита вертикальными и горизонтальными прямыми на одинаковые квадраты, площадь каждого из которых равна s₀ (обычно для простоты принимают s₀ = 1, но нам здесь удобнее именно так — в общем виде). Назовём узлами точки, являющиеся вершинами квадратов, и нарисуем произвольный многоугольник, все вершины которого лежат в узлах. При этом стороны многоугольника не обязаны быть вертикальными или горизонтальными (хотя это и не возбраняется). Например, у пятиугольника на рисунке 1 только одна сторона горизонтальна, а остальные — наклонны.

Подсчитаем количество узлов, попавших строго внутрь многоугольника (на рисунке 1 они выделены красным цветом), а также количество узлов, оказавшихся на границе многоугольника. Заметим, что на границе находятся, во-первых, все вершины многоугольника (синие), а также те узлы, что волею случая оказались на сторонах (зелёные). В частности, у нашего пятиугольника имеется 39 красных узлов, а синих, разумеется, 5 (в каждой вершине), и плюс ещё 12 зелёных на сторонах. Итого на границе 5 + 12 = 17 узлов.

Георг Пик доказал, что площадь S любого такого многоугольника зависит только от количества вершин каждого типа, то есть S есть функция от числа вершин В, лежащих внутри многоугольника, и от числа вершин Г, попавших на границу, и эту функцию можно записать в виде формулы (её-то и называют формулой Пика):

S (В, Г) = (В + 0,5 Г – 1) · s₀.

Вернувшись к тому же пятиугольнику на рисунке 1, мы без труда найдём его площадь. Здесь В = 39, Г = 17, и потому площадь равна S (39, 17) = (39 + 0,5 · 17 – 1) · s₀ = 46,5 · s₀. А попробуйте-ка подсчитать «вручную»!¹

Сила формулы Пика ещё и в том, что форма многоугольника, оказывается, в каком-то смысле «вторична», главное — количество тех или иных узлов. Например, на рисунке 2 изображены несколько разных многоугольников, но у них всех В = 0 и Г = 4, потому площади их одинаковы (кстати, чему они равны?).

Формула Пика столь изящна, что не хочется верить, будто она работает только для квадратной решётки. И действительно, формула Пика применима для любой бесконечной сетки, состоящей из равных параллелограммов, и внешне выглядит точно так же (если площадь «элементарного» параллелограмма равна s₀). То есть все «растяжки» и «перекосы», превращающие квадрат в параллелограмм, ничуть не сказываются на её справедливости.

Но и это далеко не всё. С не меньшим успехом можно разбить плоскость прямыми трёх направлений (под углами 60° друг к другу) на одинаковые треугольники (рис. 3). Представим себе многоугольник, вершины которого лежат в узлах этой треугольной решётки, и зададимся вопросом: не будет ли площадь S этакого многоугольника тоже зависеть только от количества узлов, попавших внутрь (В) и на границу (Г) многоугольника, и если да — то какова эта зависимость S (В, Г)? Площадь каждого из «элементарных» треугольников, на которые разбита плоскость, мы считаем равной s₀. Иными словами, существует ли для такой сетки аналог формулы Пика (которую уместно назвать треугольной формулой Пика)?

Оказывается, да! Чтобы в этом убедиться, сначала у сетки, изображённой на рисунке 3, удалим все прямые одного из трёх направлений (например, идущие с «северо-запада» на «юго-восток»). Получится «ромбическая» сетка, где каждый ромб образован объединением двух треугольников (рис. 4), и потому площадь такого «элементарного» ромба равна 2 s₀. Вместе с тем, после удаления всех прямых одного направления ни один узел не пропал — просто теперь в каждом узле пересекаются не три, а две прямые. И если на сетке был нарисован многоугольник с вершинами в узлах, то его граница будет проходить через столько же узлов, сколько и ранее, да и количество узлов внутри многоугольника не изменится.

А поскольку ромб — частный случай параллелограмма, для указанной сетки можно применить формулу Пика (помня, что площадь элементарного ромба равна не s₀, а 2 s₀). Разумеется, она же окажется верной и для исходной треугольной сетки. Итак, для треугольной сетки площадь многоугольника с вершинами в узлах сетки находится по формуле:

S_треуг. (В, Г) = (В + 0,5 Г – 1) · 2 s₀ = (2 В + Г – 2) · s₀.

Можно двинуться и дальше. Рассмотрим сетку, напоминающую кирпичную кладку (рис. 5), на которой одинаковые «прямоугольники-кирпичи» образуют полосы, сдвинутые на «полкирпича» относительно соседней полосы. Не поискать ли для неё аналог формулы Пика? Здесь, разумеется, узлами считаем все точки, являющиеся вершинами какого-либо элементарного прямоугольника, площадь которого, по традиции, примем равной s₀.

К счастью, и здесь успех гарантирован. Надо всего лишь каждый прямоугольник разбить по вертикали на два «полукирпича». В результате получится «типовая» сетка из прямоугольников, образуемых двумя семействами прямых, для которой формула Пика очень даже применима. Надо лишь учесть, что здесь (в противоположность рассмотренной выше треугольной сетке) элементарный прямоугольник будет вдвое меньше исходного, и потому его площадь равна 0,5 s₀. Поэтому для «кирпичной» сетки формула Пика такова:

S_кирп_. (В, Г) = (В + 0,5 Г – 1) · 0,5 s₀ = (0,5 В + 0,25 Г – 0,5) · s₀.

А сейчас предлагаем читателю самостоятельно найти аналог формулы Пика для сетки, состоящей из равных прямоугольных треугольников. Она получается из обычной квадратной сетки, если каждый её квадрат обеими диагоналями разрезать на четыре равные части (рис. 6). Разумеется, здесь s₀ — площадь каждого прямоугольного треугольника, на которые разделена плоскость. А потом сверьтесь с ответом.

Ответ

В разбиении плоскости на прямоугольные треугольники уберём все горизонтальные и вертикальные прямые. Получится квадратная сетка, образованная пересекающимися наклонными прямыми, в ней каждый квадрат «склеен» из двух прямоугольных треугольников (и «пропавших» узлов нет!). Площадь такого квадрата равна 2 s₀, и потому формула Пика выглядит точь-в-точь как для сетки из правильных треугольников:

S (В, Г) = (В + 0,5 Г – 1) ·2 s₀ = (2 В + Г – 2) · s₀.

А для шестиугольной сетки аналога формулы Пика нет! Чтобы в этом убедиться, рассмотрим одну шестиугольную ячейку ABCDEF сетки (рисунок справа). Сравним треугольники ABF и ACF. У них основание AF — общее, но третьи вершины (B и C) находятся на разных расстояниях от прямой AF. Тогда площади их заведомо различны. С другой стороны, количества точек, попавших на границу и внутрь каждого треугольника, одинаковы: Г = 3, В = 0. Поэтому аналог формулы Пика (если бы он существовал) дал бы одинаковые значения их площадей. Противоречие!

В заключение вспомним, что плоскость можно разделить не только на равные квадраты и треугольники, но и на шестиугольники — наподобие пчелиных сот (рис. 7). Может, и для такой сетки существует аналог формулы Пика? Попробуйте это выяснить.

Существуют, кстати, обобщения формулы Пика для определения объёмов тел в трёхмерном пространстве (и даже в пространствах более высоких размерностей) — так называемый многочлен Эрхарта. Но это очень сложная тема, уводящая слишком далеко. Поэтому углубляться не будем.

Художник Алексей Вайнер

¹ Конечно, тоже не ахти какая сложность — надо лишь разбить многоугольник на прямоугольники и прямоугольные треугольники, но повозиться придётся всё-таки дольше.

Источник

From Wikipedia, the free encyclopedia

Farey sunburst of order 6, with 1 interior (red) and 96 boundary (green) points giving an area of 1 + 96/2 − 1 = 48^[1]

In geometry, Pick’s theorem provides a formula for the area of a simple polygon with integer vertex coordinates, in terms of the number of integer points within it and on its boundary. The result was first described by Georg Alexander Pick in 1899.^[2] It was popularized in English by Hugo Steinhaus in the 1950 edition of his book Mathematical Snapshots.^[3]^[4] It has multiple proofs, and can be generalized to formulas for certain kinds of non-simple polygons.

Formula[edit]

i = 7, b = 8, A = i + b/2 − 1 = 10

Suppose that a polygon has integer coordinates for all of its vertices. Let be the number of integer points interior to the polygon, and let be the number of integer points on its boundary (including both vertices and points along the sides). Then the area of this polygon is:^[5]^[6]^[7]^[8]

${displaystyle A=i+{frac {b}{2}}-1.}$

The example shown has interior points and boundary points, so its area is ${displaystyle A=7+{tfrac {8}{2}}-1=10}$ square units.

Proofs[edit]

Via Euler’s formula[edit]

One proof of this theorem involves subdividing the polygon into triangles with three integer vertices and no other integer points. One can then prove that each subdivided triangle has area exactly ${tfrac {1}{2}}$ . Therefore, the area of the whole polygon equals half the number of triangles in the subdivision. After relating area to the number of triangles in this way, the proof concludes by using Euler’s polyhedral formula to relate the number of triangles to the number of grid points in the polygon.^[5]

Tiling of the plane by copies of a triangle with three integer vertices and no other integer points, as used in the proof of Pick’s theorem

The first part of this proof shows that a triangle with three integer vertices and no other integer points has area exactly ${tfrac {1}{2}}$ , as Pick’s formula states. The proof uses the fact that all triangles tile the plane, with adjacent triangles rotated by 180° from each other around their shared edge.^[9] For tilings by a triangle with three integer vertices and no other integer points, each point of the integer grid is a vertex of six tiles. Because the number of triangles per grid point (six) is twice the number of grid points per triangle (three), the triangles are twice as dense in the plane as the grid points. Any scaled region of the plane contains twice as many triangles (in the limit as the scale factor goes to infinity) as the number of grid points it contains. Therefore, each triangle has area ${tfrac {1}{2}}$ , as needed for the proof.^[5] A different proof that these triangles have area ${tfrac {1}{2}}$ is based on the use of Minkowski’s theorem on lattice points in symmetric convex sets.^[10]

Subdivision of a grid polygon into special triangles

This already proves Pick’s formula for a polygon that is one of these special triangles. Any other polygon can be subdivided into special triangles: add non-crossing line segments within the polygon between pairs of grid points until no more line segments can be added. The only polygons that cannot be subdivided in this way are the special triangles considered above; therefore, only special triangles can appear in the resulting subdivision. Because each special triangle has area ${tfrac {1}{2}}$ , a polygon of area will be subdivided into special triangles.^[5]

The subdivision of the polygon into triangles forms a planar graph, and Euler’s formula gives an equation that applies to the number of vertices, edges, and faces of any planar graph. The vertices are just the grid points of the polygon; there are of them. The faces are the triangles of the subdivision, and the single region of the plane outside of the polygon. The number of triangles is , so altogether there are faces. To count the edges, observe that there are sides of triangles in the subdivision. Each edge interior to the polygon is the side of two triangles. However, there are edges of triangles that lie along the polygon’s boundary and form part of only one triangle. Therefore, the number of sides of triangles obeys the equation , from which one can solve for the number of edges, ${displaystyle E={tfrac {6A+b}{2}}}$ . Plugging these values for , , and into Euler’s formula gives

${displaystyle (i+b)-{frac {6A+b}{2}}+(2A+1)=2.}$

Pick’s formula is obtained by solving this linear equation for .^[5] An alternative but similar calculation involves proving that the number of edges of the same subdivision is , leading to the same result.^[11]

It is also possible to go the other direction, using Pick’s theorem (proved in a different way) as the basis for a proof of Euler’s formula.^[6]^[12]

Other proofs[edit]

Alternative proofs of Pick’s theorem that do not use Euler’s formula include the following.

One can recursively decompose the given polygon into triangles, allowing some triangles of the subdivision to have area larger than 1/2. Both the area and the counts of points used in Pick’s formula add together in the same way as each other, so the truth of Pick’s formula for general polygons follows from its truth for triangles. Any triangle subdivides its bounding box into the triangle itself and additional right triangles, and the areas of both the bounding box and the right triangles are easy to compute. Combining these area computations gives Pick’s formula for triangles, and combining triangles gives Pick’s formula for arbitrary polygons.^[7]^[8]^[13]
Alternatively, instead of using grid squares centered on the grid points, it is possible to use grid squares having their vertices at the grid points. These grid squares cut the given polygon into pieces, which can be rearranged (by matching up pairs of squares along each edge of the polygon) into a polyomino with the same area.^[14]
Pick’s theorem may also be proved based on complex integration of a doubly periodic function related to Weierstrass elliptic functions.^[15]
Applying the Poisson summation formula to the characteristic function of the polygon leads to another proof.^[16]

Pick’s theorem was included in a 1999 web listing of the «top 100 mathematical theorems», which later became used by Freek Wiedijk as a benchmark set to test the power of different proof assistants. As of 2021, Pick’s theorem had been formalized and proven in only one of the ten proof assistants recorded by Wiedijk.^[17]

Generalizations[edit]

i = 2, b = 12, h = 1, A = i + b/2 + h − 1 = 8

Generalizations to Pick’s theorem to non-simple polygons are more complicated and require more information than just the number of interior and boundary vertices.^[3]^[18] For instance, a polygon with holes bounded by simple integer polygons, disjoint from each other and from the boundary, has area^[19]

${displaystyle A=i+{frac {b}{2}}+h-1.}$

It is also possible to generalize Pick’s theorem to regions bounded by more complex planar straight-line graphs with integer vertex coordinates, using additional terms defined using the Euler characteristic of the region and its boundary,^[18] or to polygons with a single boundary polygon that can cross itself, using a formula involving the winding number of the polygon around each integer point as well as its total winding number.^[3]

Reeve tetrahedra showing that Pick’s theorem does not apply in higher dimensions

The Reeve tetrahedra in three dimensions have four integer points as vertices and contain no other integer points, but do not all have the same volume. Therefore, there does not exist an analogue of Pick’s theorem in three dimensions that expresses the volume of a polyhedron as a function only of its numbers of interior and boundary points.^[20] However, these volumes can instead be expressed using Ehrhart polynomials.^[21]^[22]

[edit]

Several other mathematical topics relate the areas of regions to the numbers of grid points. Blichfeldt’s theorem states that every shape can be translated to contain at least its area in grid points.^[23] The Gauss circle problem concerns bounding the error between the areas and numbers of grid points in circles.^[24] The problem of counting integer points in convex polyhedra arises in several areas of mathematics and computer science.^[25]
In application areas, the dot planimeter is a transparency-based device for estimating the area of a shape by counting the grid points that it contains.^[26] The Farey sequence is an ordered sequence of rational numbers with bounded denominators whose analysis involves Pick’s theorem.^[27]

Another simple method for calculating the area of a polygon is the shoelace formula. It gives the area of any simple polygon as a sum of terms computed from the coordinates of consecutive pairs of its vertices. Unlike Pick’s theorem, the shoelace formula does not require the vertices to have integer coordinates.^[28]

References[edit]

^ Kiradjiev, Kristian (October 2018). «Connecting the dots with Pick’s theorem» (PDF). Mathematics Today. pp. 212–214.
^ Pick, Georg (1899). «Geometrisches zur Zahlenlehre». Sitzungsberichte des deutschen naturwissenschaftlich-medicinischen Vereines für Böhmen «Lotos» in Prag. (Neue Folge). 19: 311–319. JFM 33.0216.01. CiteBank:47270
^ ^a ^b ^c Grünbaum, Branko; Shephard, G. C. (February 1993). «Pick’s theorem». The American Mathematical Monthly. 100 (2): 150–161. doi:10.2307/2323771. JSTOR 2323771. MR 1212401.
^ Steinhaus, H. (1950). Mathematical Snapshots. Oxford University Press. p. 76. MR 0036005.
^ ^a ^b ^c ^d ^e Aigner, Martin; Ziegler, Günter M. (2018). «Three applications of Euler’s formula: Pick’s theorem». Proofs from THE BOOK (6th ed.). Springer. pp. 93–94. doi:10.1007/978-3-662-57265-8. ISBN 978-3-662-57265-8.
^ ^a ^b Wells, David (1991). «Pick’s theorem». The Penguin Dictionary of Curious and Interesting Geometry. Penguin Books. pp. 183–184.
^ ^a ^b Beck, Matthias; Robins, Sinai (2015). «2.6 Pick’s theorem». Computing the Continuous Discretely: Integer-Point Enumeration in Polyhedra. Undergraduate Texts in Mathematics (2nd ed.). Springer. pp. 40–43. doi:10.1007/978-1-4939-2969-6. ISBN 978-1-4939-2968-9. MR 3410115.
^ ^a ^b Ball, Keith (2003). «Chapter 2: Counting Dots». Strange Curves, Counting Rabbits, and Other Mathematical Explorations. Princeton University Press, Princeton, NJ. pp. 25–40. ISBN 0-691-11321-1. MR 2015451.
^ Martin, George Edward (1982). Transformation geometry. Undergraduate Texts in Mathematics. Springer-Verlag. Theorem 12.1, page 120. doi:10.1007/978-1-4612-5680-9. ISBN 0-387-90636-3. MR 0718119.
^ Ram Murty, M.; Thain, Nithum (2007). «Pick’s theorem via Minkowski’s theorem». The American Mathematical Monthly. 114 (8): 732–736. doi:10.1080/00029890.2007.11920465. JSTOR 27642309. MR 2354443. S2CID 38855683.
^ Funkenbusch, W. W. (June–July 1974). «From Euler’s formula to Pick’s formula using an edge theorem». Classroom Notes. The American Mathematical Monthly. 81 (6): 647–648. doi:10.2307/2319224. JSTOR 2319224. MR 1537447.
^ DeTemple, Duane; Robertson, Jack M. (March 1974). «The equivalence of Euler’s and Pick’s theorems». The Mathematics Teacher. 67 (3): 222–226. doi:10.5951/mt.67.3.0222. JSTOR 27959631. MR 0444503.
^ Varberg, Dale E. (1985). «Pick’s theorem revisited». The American Mathematical Monthly. 92 (8): 584–587. doi:10.2307/2323172. JSTOR 2323172. MR 0812105.
^ Trainin, J. (November 2007). «An elementary proof of Pick’s theorem». The Mathematical Gazette. 91 (522): 536–540. doi:10.1017/S0025557200182270. JSTOR 40378436. S2CID 124831432.
^ Diaz, Ricardo; Robins, Sinai (1995). «Pick’s formula via the Weierstrass -function«. The American Mathematical Monthly. 102 (5): 431–437. doi:10.2307/2975035. JSTOR 2975035. MR 1327788.
^ Brandolini, L.; Colzani, L.; Robins, S.; Travaglini, G. (2021). «Pick’s theorem and convergence of multiple Fourier series». The American Mathematical Monthly. 128 (1): 41–49. doi:10.1080/00029890.2021.1839241. MR 4200451. S2CID 231624428.
^ Wiedijk, Freek. «Formalizing 100 Theorems». Radboud University Institute for Computing and Information Sciences. Retrieved 2021-07-10.
^ ^a ^b Rosenholtz, Ira (1979). «Calculating surface areas from a blueprint». Mathematics Magazine. 52 (4): 252–256. doi:10.1080/0025570X.1979.11976797. JSTOR 2689425. MR 1572312.
^ Sankar, P. V.; Krishnamurthy, E. V. (August 1978). «On the compactness of subsets of digital pictures». Computer Graphics and Image Processing. 8 (1): 136–143. doi:10.1016/s0146-664x(78)80021-5.
^ Reeve, J. E. (1957). «On the volume of lattice polyhedra». Proceedings of the London Mathematical Society. Third Series. 7: 378–395. doi:10.1112/plms/s3-7.1.378. MR 0095452.
^ Beck & Robins (2015), 3.6 «From the discrete to the continuous volume of a polytope», pp. 76–77
^ Diaz, Ricardo; Robins, Sinai (1997). «The Ehrhart polynomial of a lattice polytope». Annals of Mathematics. Second Series. 145 (3): 503–518. doi:10.2307/2951842. JSTOR 2951842. MR 1454701.
^ Olds, C. D.; Lax, Anneli; Davidoff, Giuliana P. (2000). «Chapter 9: A new principle in the geometry of numbers». The Geometry of Numbers. Anneli Lax New Mathematical Library. Vol. 41. Mathematical Association of America, Washington, DC. pp. 119–127. ISBN 0-88385-643-3. MR 1817689.
^ Guy, Richard K. (2004). «F1: Gauß’s lattice point problem». Unsolved Problems in Number Theory. Problem Books in Mathematics. Vol. 1 (3rd ed.). New York: Springer-Verlag. pp. 365–367. doi:10.1007/978-0-387-26677-0. ISBN 0-387-20860-7. MR 2076335.
^ Barvinok, Alexander (2008). Integer Points In Polyhedra. Zurich Lectures in Advanced Mathematics. Zürich: European Mathematical Society. doi:10.4171/052. ISBN 978-3-03719-052-4. MR 2455889.
^ Bellhouse, D. R. (1981). «Area estimation by point-counting techniques». Biometrics. 37 (2): 303–312. doi:10.2307/2530419. JSTOR 2530419. MR 0673040.
^ Bruckheimer, Maxim; Arcavi, Abraham (1995). «Farey series and Pick’s area theorem». The Mathematical Intelligencer. 17 (4): 64–67. doi:10.1007/BF03024792. MR 1365013. S2CID 55051527.
^ Braden, Bart (1986). «The surveyor’s area formula» (PDF). The College Mathematics Journal. 17 (4): 326–337. doi:10.2307/2686282. JSTOR 2686282.

External links[edit]

Pick’s Theorem by Ed Pegg, Jr., the Wolfram Demonstrations Project.
Pi using Pick’s Theorem by Mark Dabbs, GeoGebra

Источник

Формула Пика. Рассказ о формуле, при помощи которой можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник). Это формула Пика.

Она секретной не является. Информация о ней в интернете имеется, но многим материал статьи будет крайне полезен. Об этой формуле обычно рассказывается применительно к нахождению площади треугольника. На примере треугольника мы её и рассмотрим.

В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.

ФОРМУЛА ПИКА

Площадь искомой фигуры можно найти по формуле:

М – количество узлов на границе треугольника (на сторонах и вершинах)

N – количество узлов внутри треугольника

*Под «узлами» имеется ввиду пересечение линий.

Найдём площадь треугольника:

Отметим узлы:

1 клетка = 1 см

M = 15 (обозначены красным)

N = 34 (обозначены синим)

Ещё пример. Найдём площадь параллелограмма:

Отметим узлы:

M = 18 (обозначены красным)

N = 20 (обозначены синим)

Найдём площадь трапеции:

Отметим узлы:

M = 24 (обозначены красным)

N = 25 (обозначены синим)

Найдём площадь многоугольника:

Отметим узлы:

M = 14 (обозначены красным)

N = 43 (обозначены синим)

Понятно, что находить площадь трапеции, параллелограмма, треугольника проще и быстрее по соответствующим формулам площадей этих фигур. Но знайте, что можно это делать и таким образом.

А вот когда дан многоугольник, у которого пять и более углов эта формула работает хорошо.

Теперь взгляните на следующие фигуры:

Это типовые фигуры, в заданиях стоит вопрос о нахождении их площади. Такие или подобные им будут на ЕГЭ. При помощи формулы Пика такие задачи решаются за минуту. Например, найдём площадь фигуры:

Отметим узлы:

M = 11 (обозначены красным)

N = 5 (обозначены синим)

Ответ: 9,5

Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см. Ответ дайте в квадратных сантиметрах.

Посмотреть решение

Конечно, можно и эти «микрофигурки» дробить на более простые фигуры (треугольники, трапеции). Способ решения выбирать вам.

Рассмотрим подход оговоренный в статье «Площадь четырёхугольника. Универсальный способ«.

Найдём площадь фигуры:

Опишем около неё прямоугольник:

Из площади прямоугольника (в данном случае это квадрат) вычтем площади полученных простых фигур:

Ответ: 4,5

В будущем будем рассматривать задания на нахождение площади, связанные с окружностями построенными на листе в клетку, не пропустите! На этом всё. Успехов вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

Вокруг формулы Пика

Игорь Акулич «Квантик» №8, 2021

Ответ

Formula[edit]

Proofs[edit]

Via Euler’s formula[edit]

Other proofs[edit]

Generalizations[edit]

[edit]

References[edit]

External links[edit]

Игорь Акулич
«Квантик» №8, 2021