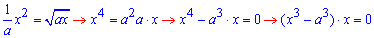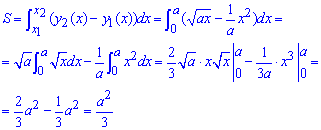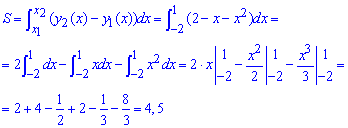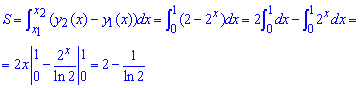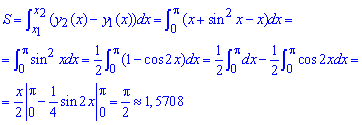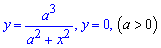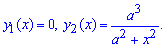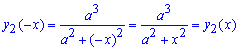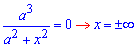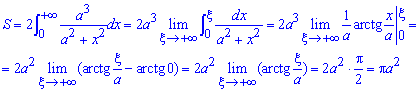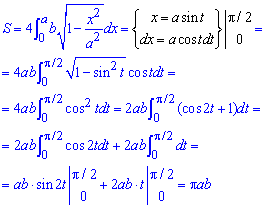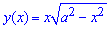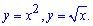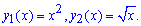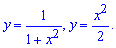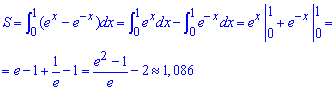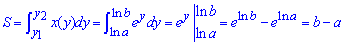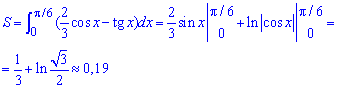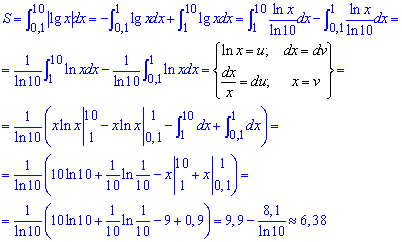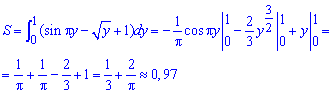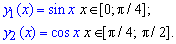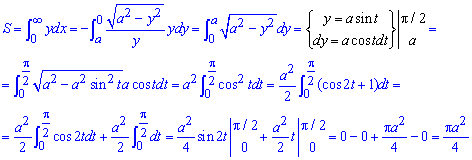Центральная симметрия подсказывает идею модели, иллюстрирующую подсчёт площади. На листе бумаги распечатаем график синуса и закрасим под ним
площадь на отрезке $[-pi/2, pi/2]$. На «прозрачке» повторим картинку.
Если наложить прозрачку на бумажный график, то картинки, естественно, совпадут. Воткнув канцелярскую скрепку в начало координат, повернём
прозрачку на $180^circ$. Кривая синуса совпадёт с собой! А вот закрашенным, причём без наложений, окажется уже весь прямоугольник $[-pi/2, pi/2]times [-1,1]$. Посчитать площадь прямоугольника, а затем поделить пополам, — несложно.
Итак, площадь под синусом (между графиком функции $sin x$ и его «основанием») на участке $[-pi/2, pi/2]$ равна $pi$, а на полном периоде, соответственно, $2pi$. Этот факт в совокупности с лепестками Роберваля, о которых будет отдельный сюжет, дают способ вычислить площадь под аркой циклоиды.
По сути, модель основана на том, что синусоида делит прямоугольник на две равновеликие части. Подобный трюк, очевидно, можно проводить
и с другими нечётными (или сводящимися к ним) функциями.
Площадь фигуры ограниченной линиями
Что умеет?
- Находит точки пересечения указанных кривых линий
- Умный робот определяет области, где лежат фигуры, чтобы вычислить их площади. Он делает это, находя точки, где графики пересекаются.
- Помогает находить площади под графиками, вычисляя интегралы.

Примеры кривых
- С осями ординат x и y
-
y = x^2 + 1 y = 0 x = -1 x = 2
- Графики, заданные неявным образом
-
y = 3 xy = 2 y^2 - x^2 = 3
- Две окружности
-
x^2 + y^2 = 4 x^2 + y^2 = 9
- В полярных координатах
-
r = 2(1 - cos(p)) r = 2
- Парабола и прямая линия
-
y = (x + 2)^2 y = 4
-
y = (x + 2)^2 y = 1 - x
-
y = x^2 x + y = 2
- Корень квадратный
-
y = x^2 y = sqrt(x)
- С экспонентой и численным решением
-
y = (2x+3)*e^(-x) x^2 = y
- Параметрически-заданная функция
-
x = 2(t - sint) y = 3(1 - cost)
Указанные выше примеры содержат также:
- модуль или абсолютное значение: absolute(x) или |x|
-
квадратные корни sqrt(x),
кубические корни cbrt(x) -
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
-
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
арккотангенс acot(x) -
натуральные логарифмы ln(x),
десятичные логарифмы log(x) -
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x),
гиперболический тангенс и котангенс tanh(x), ctanh(x) -
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x) -
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x),
арккосеканс acsc(x), гиперболический секанс sech(x),
гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
гиперболический арккосеканс acsch(x) -
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x) -
знак числа:
sign(x) -
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности),
функция Лапласа laplace(x) -
Факториал от x:
x! или factorial(x) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
-
Тригонометрические интегралы: Si(x),
Ci(x),
Shi(x),
Chi(x)
Правила ввода
Можно делать следующие операции
- 2*x
- — умножение
- 3/x
- — деление
- x^2
- — возведение в квадрат
- x^3
- — возведение в куб
- x^5
- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- Действительные числа
- вводить в виде 7.5, не 7,5
Постоянные
- pi
- — число Пи
- e
- — основание натурального логарифма
- i
- — комплексное число
- oo
- — символ бесконечности
-
Log in
-
Join
Watch in our app
Open in app
|
|
Найти площадь части синусоиды — как?
|
|
13/07/07 |
Найти площадь части синусоиды от 0 до pi/2 в зависимости от частоты этой синусоиды(под частотой я имею в виду множитель b в формуле y:=a*sin(b*x)
То есть —
Понятно что взять интеграл, но это и не получается, не силён я в них.
|
|
|
|
|
photon |
|
||
23/12/05 |
led9 писал(а): Понятно что взять интеграл, но это и не получается, не силён я в них. Если Вы хотите научиться сам считать площадь под кривой, то придется-таки осваивать интегралы, если для Вас важен только ответ — мат.пакеты вам в помощь: даже MathCAD даст вам аналитическое решение
|
||
|
|
|||
|
led9 |
|
|
13/07/07 |
photon
|
|
|
|
|
photon |
|
||
23/12/05 |
|||
|
|
|||
|
Толь Толич |
|
|
15/07/07 |
|
|
|
|
|
незваный гость |
|
||
17/10/05 |
1) Четверть периода равны , это
2) Под 3) Если же аккуратно подставить правильный верхний предел, то получится в точности формула photon а.
|
||
|
|
|||
|
AD |
|
||
17/06/06 |
На примитивном уровне можно считать так:
Синусоида led9 писал(а): неужели если частота в два раза больше, то два кривых горба в точности сравняются с одним по площади?
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Площадь фигуры между двумя кривыми в прямоугольных координатах определяется интегралом
от разницы кривых, где одна из них всегда принимает не меньшие значения чем другая
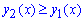
Пределы интегрирования — прямые x1=a, x2=b — ограничивают фигуру (a<b чаще всего это точки пересечения заданных кривых).
Данный цикл задач в первую очередь подойдет студентам мех-мата Львовского национального университета имени Ивана Франко для прохождения практикума из математического анализа.
Студенты других Вузов могут набираться практики на подобных интегралах, и изучать методику вычисления.
Первый номер в примерах отвечает номеру основного задания из сборника М. В. Заболоцький, Фединяк С.И., Филевич П.В. «Практикум из математического анализа» (рядом стоит номер из сборника Б. П. Демидовича).
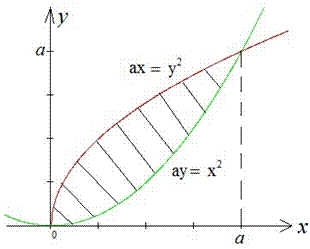
Пример 2.81 (2397). Найти площадь фигуры, ограниченной кривыми, заданными в прямоугольных координатах ax=y2, ay=x2,(a>0).
Вычисление: Построим графики функций, которые ограничивают искомую площадь фигуры: 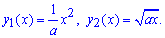
На графике они будут иметь следующий вид
Площадь между кривыми и нужно найти. Как правило, Вам редко будет известно сам график, поэтому в заданиях где не заданы области на которой находить площадь в первую очередь необходимо найти точки пересечения кривых.
Найдем пределы интегрирования, то есть точки абсцисс пересечения заданных функций y1(x)=y2(x):
Как видите таким условием есть условие равенства функций.
Из последнего уравнения получим две точки x1=0, x2=a.
Дальше, когда Вы не видите графика функций необходимо установить какая из кривых принимает большие значения. Это нужно лишь для того, чтобы с первого раза получить положительное значение площади фигуры. Поскольку площадь всегда больше нуля, а интеграл может принимать произвольные значения, то без проверки следующего условия для нахождения площади интеграл нужно брать за модулем.
Выбираем произвольную точку из отрезка интегрирования [0;a] и убеждаемся в правильности неравенства 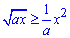
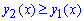
Как отмечалось выше, это нужно для того, чтобы после интегрирования получить положительную площадь фигуры между кривыми.
Вычисляем площадь фигуры, которая ограничена заданными кривыми интегрированиям:
Здесь мы имели достаточно простые функции, поэтому возведя их к табличным интегралам найти площадь достаточно легко. Следующие примеры будут содержать все более тяжелые функции, для интегрирования которых нужно применять знание практически всех формул интегрирования.
Следует заметить: значения площадей (во всех заданиях) измеряются в квадратных единицах (кв. од.), об этом Вы должны помнить, однако для экономии места и времени здесь будут приведены лишь значения определенных интегралов.
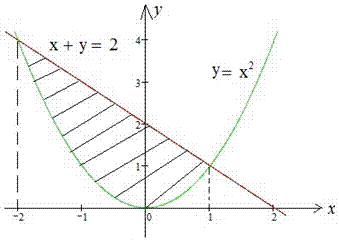
Пример 2.82 (2398) Вычислить площадь фигуры, ограниченной кривыми y=x2, x+y=2.
Вычисление: По методике записываем уравнение кривых, которые ограничивают площадь фигуры:
y1(x)=x2, y2(x)=2-x.
Здесь функции выразить достаточно просто.
Вычислим пределы интегрирования, приравняв между собой функции y1(x)=y2(x):
x2=2-x.
Переносим переменные по одну сторону от знака равенства и решаем квадратное уравнение
x2+x-2=0;
(x+2)(x-1)=0.
Следовательно, корни уравнения x1=-2, x2=1.
Сам график кривых и фигуры, площадь которой ищем, приведен на рисунку
Подстановкой любой точки из промежутка [-2;1], например x=0 в функции убеждаемся, что выполняется неравенство
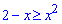
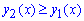
Площадь фигуры вычисляем интегрированием разницы кривых в найденных пределах:
Площадь равна S=4,5 квадратных единиц.
По физическому содержанию площадь фигуры равна разнице площадей двух криволинейных трапеций. Первая отвечает за верхний график y2(x), нижняя криволинейная трапеция за функцию, которая принимает меньшие значения y2(x). Разница заключается в том, что здесь еще нужно определять пределы интегрирования.
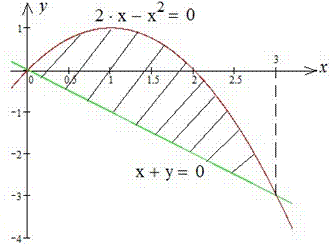
Пример 2.83 (2399) Найти площадь фигуры, ограниченной кривыми y=2x-x2, x+y=0.
Вычисление: Запишем уравнение кривых, которые ограничивают искомую фигуру:
y1(x)=-x, y2(x)=2x-x2.
Из условия равенства функций y1(x)=y2(x) найдем пределы интегрирования:
2x-x2=-x;
x2-3x=0;
x (x-3) =0.
Следовательно, x1=0, x2=3.
Подстановкой единицы видим, что на промежутке [0;3] исполняется неравенство
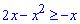
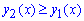
Находим площадь фигуры ограниченной заданными кривыми:
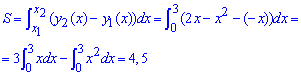
Под интегралом простая квадратичная функция, поэтому само интегрирование не сложно.
Следующие функции будут более сложными в плане интегрирования, однако используя табличные интегралы площадь найти удается.
Пример 2.84 (2400) Найти площадь фигуры, ограниченной кривыми y=2x, y=2, x=0.
Вычисление: Запишем подынтегральные функции:
y1(x)=2x, y2(x)=2, а также прямую x1=0 (ограничивает фигуру по оси абсцисс).
Найдем вторую границу интегрирования из условия равенства функций y1(x)=y2(x):
2x=2, 2x=21, отсюда имеем вторую точку x1=1.
На промежутке [0;1] исполняется неравенство 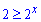
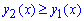
График степенной функции и прямой приведен ниже.
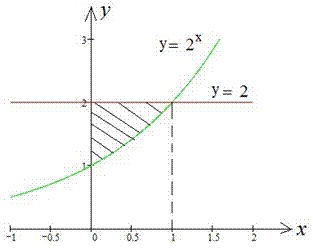
Площадь фигуры, которая ограничена кривыми равна интегралу:
При интегрировании получим логарифм.
На калькуляторах можете проверить, что площадь положительна.
Пример 2.85 (2401) Вычислить площадь фигуры, ограниченной кривыми y=x, y=x+sin2x, 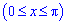
Вычисление: Запишем уравнение кривых, которые ограничивают площадь фигуры:
y1(x)=x, y2(x)=x+sin2x.
Дальше пределы интегрирования:
x1=0, x2=Pi (это известно нам по условию).
На промежутке 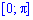
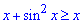
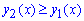
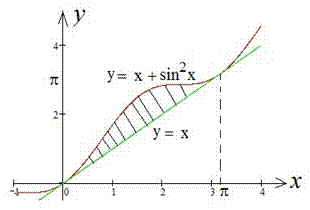
Если бы существовала дополнительная точка пересечения, то площадь была бы равна сумме двух интегралов.
Площадь фигуры вычисляем интегрированием: квадрат синуса под интегралом понижаем и выражаем с помощью косинуса двойного угла, а дальше за классической формулой интегрирования
Площадь равна Pi/2, что приблизительно равно 1,5708.
Пример 2.86 (2402) Найти площадь фигуры, ограниченной кривыми
Вычисление: Переписываем функции
Найдем пределы интегрирования, то есть точки абсцисс пересечения заданных функций из условия y1(x)=y2(x):
Поскольку функция парная
то найдем половину площади и результат умножим на двойку.
Из условия находим
что пределы равны плюс, минус бесконечности.
Чтобы легко представить, что мы интегрируем наведем график подынтегральных функций
Учитывая четность функции интегрировать будем от 0 к бесконечности 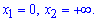
Получим несвойственный интеграл первого рода (детальнее о нем в части ІІІ).
Площадь фигуры вычисляем через предел интеграла:
В результате интегрирования получим арктангенс, который в предельном случае стремится к Pi/2.
Конечная формула достаточно компактна и удобна для расчетов, хотя с таким типом интегралов Вы знакомитесь впервые.
Пример 2.87 (2403) Вычислить площадь фигуры, ограниченной кривыми
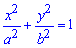
Вычисление: Все Вы должны знать, что такой формулой задается уравнение эллипса.
Так как оси эллипса в канонической системе координат являются его осями симметрии, то эти оси делят эллипс на 4 равные части. Поэтому будем рассматривать часть эллипса, который находится в первом квадранте канонической (прямоугольной) системы координат.
Выражаем уравнение функции, которая ограничивает искомую площадь (четверть эллипса):
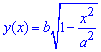
Запишем пределы интегрирования: из аналитической геометрии известно, что четверть эллипса ограничена прямыми x1=0, x2=a.
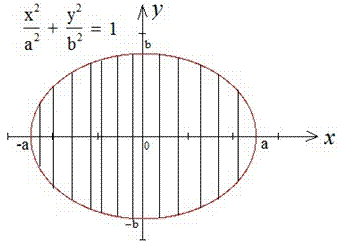
Для вычисления площади эллипса в самом интеграле необходимо выполнить замену переменных, что в свою очередь ведет к изменению пределов интегрирование. При этом придем к квадрату косинуса, который понижаем через косинус двойного угла.
В конце манипуляций приходим к табличным интегралам, которые легко интегрируем и подставляем пределы:
Получили классическую формулу площади эллипса S=Pi*a*b .
Видим, если эллипс вырождается в круг при (a=b=R), тогда формула площади круга S=Pi*R2.
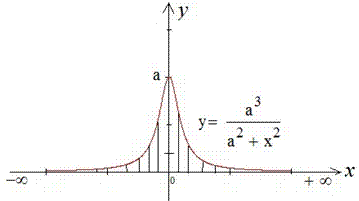
Пример 2.88 (2404) Вычислить площадь фигуры, ограниченной кривыми y2=x2(a2-x2).
Вычисление: Так как все переменные в заданном уравнении входят в квадратах, то оси прямоугольной системы координат являются осями симметрии фигуры, которая ограничена этой линией, потому эти оси делят заданную фигуру на 4 равных части. Достаточно рассмотреть часть фигуры, которая заходиться в первом квадранте прямоугольной системы координат.
Построим график функции, которая ограничивает искомую площадь четвертины фигуры:
График неизвестной фигуры подобен на крылья бабочки.
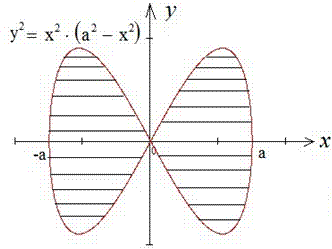
При y=0 имеем два корня уравнения x1=0 и x2=a.
Площадь фигуры равна 4 умножить на интеграл с найденными пределами.
Во время интегрирования выполняем замену переменных и пределов интегрирования
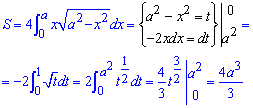
Это позволяет перейти к показательной функции, которая легко интегрируется.
Всегда помните, что замена переменных под интегралом ведет к изменению пределов интегрирования.
Пример 2.89 Найти площадь фигуры, ограниченную линиями
Вычисление: Запишем графику функций, которые ограничивают искомую площадь фигуры:
Определим пределы интегрирования из условия y1(x)=y2(x):
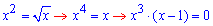
Между функциями справедлива зависимость 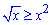
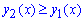
График функций, что анализируем следующий
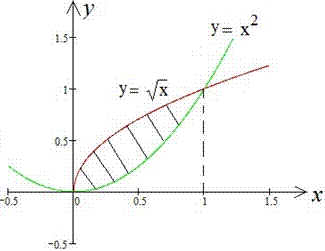
Площадь фигуры через определенный интеграл равна 1/3 (сравните 2.81 при a=1) :
Пример 2.90 Вычислить площадь фигуры, ограниченной кривыми
Вычисление: Вычислим пределы интегрирования из условия равенства функций y1(x)=y2(x):
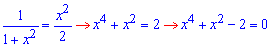
Из биквадратного уравнения получим значение точек пересечения:
x1=-1 и x2=1.
Сами же функции в прямоугольных координатах будут иметь вид
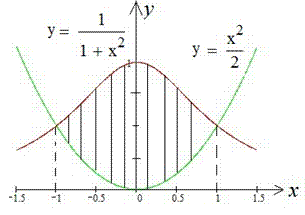
Интегрированием находим площадь фигуры (смотри рисунок и образец 2.89) :
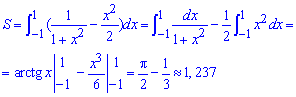
Первый интеграл даст арктангенс, запомните хорошо эту формулу.
Пример 2.91 Вычислить площадь фигуры, ограниченной кривыми y=ex, y=e-x,x=1.
Вычисление: Из условия, которое Вы из-за повторяемости должны выучить y1(x)=y2(x) находим точки пересечения кривых:
ex=e-x,x=-x, 2x=0, следовательно, x1=0.
x2=1 (известно за условием).
График функций следующий
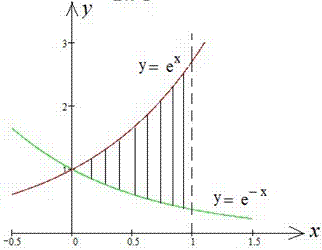
Экспоненту интегрировать не трудно, а площадь фигуры выражается формулой (смотри рисунок и образец 2.84) :
Пример 2.92 Найти площадь фигуры, ограниченной кривыми y=ln(x), y=ln2(x).
Вычисление: Пределы интегрирования из условия равенства функций y=ln(x), y=ln2(x) равны x1=1 и x2=e.

Интегрированием логарифмов находим площадь фигуры (смотри рисунок):
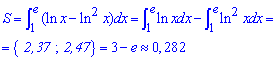
Здесь надо проинтегрировать по частям, положив ln(x) =u, (ln2(x)=u) и dx=dv. Попробуйте промежуточные действия провести самостоятельно.
Пример 2.93 Вычислить площадь фигуры, ограниченной кривыми
y=ln(x), y=ln(a), y=ln(b), x=0, где 0<a<b.
Вычисление: Построим графики функций, которые ограничивают искомую площадь фигуры:
x (y) =ey (то есть обратная функция к заданной функции y(x)=ln(x)) .
Такой прием применяют, когда пределы интегрирования параллельны оси Оx, то есть y=const.
Запишем пределы интегрирования:
y1=ln(a), y2=ln(b) (берем из начального условия).
График искомой фигуры следующий
Площадь фигуры, которая ограничена заданными кривыми:
Пример 2.94 Найти площадь фигуры, ограниченной кривыми 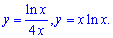
Вычисление: Пределы интегрирования в формуле площади находим из условия y1(x)=y2(x):
ln(x)/(4x)=x*ln(x).
Упростив на логарифм (если он больше нуля), получим
1=4x2; 4x2-1=0, x1=1/2.
Из условия на логарифм (=0) получим
ln(x) =0; x2=1.
ОДЗ: x>0.
График фигуры в прямоугольных координатах следующий
Площадь фигуры между кривыми (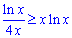
для вычисления интегралов используем метод замены переменных
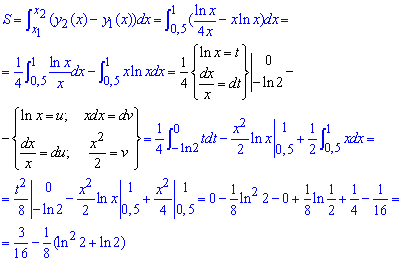
Вычисление не так просты, поэтому с превращениями попробуйте разобраться самостоятельно.
Пример 2.95 Вычислить площадь фигуры, ограниченной кривыми y=arcsin(x), y=arccos(x), y=0.
Вычисление: Находим точки пересечения кривых из равенства x1(y)=x2(y):
sin(x)=cos(y), отсюда y1=0 (известно за условием) и y1=Pi/4 (образец 2.93).
На графике это выглядит следующим образом

Учитывая справедливость неравенства 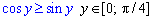
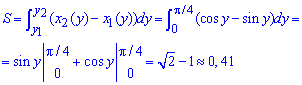
Думаю, что с такими заданиями на экзамене или модулях Вы справитесь.
Пример 2.96 Найти площадь фигуры, ограниченной кривыми y=tg(x), y=2/3*cos(x), x=0.
Вычисление: Найдем пределы интегрирования, то есть абсциссы точек пересечения заданных функций y1(x)=y2(x):
tg(x)=2/3*cos(x), отсюда 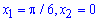
(вторая точка известна за условием).
Кривые на плоскости имеют вид
Площадь фигуры, которая ограничена заданными кривыми (
Пример 2.97 (2400) Вычислить площадь фигуры, ограниченной кривыми y=|ln(x)|, y=0, x=0,1; x=10.
Вычисление: Выписываем пределы интегрирования x1=0,1; x2=10 из начального условия.
Как строить модуль от логарифма Вы, по-видимому, еще не забыли

Площадь фигуры равна сумме двух интегралов, причем первый берем со знаком минус (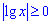
Во время интегрирования использовали интегрирование частями.
Пример 2.98 (2400) Найти площадь фигуры, ограниченной кривыми y=(x+1)2, x=sin(Pi*y), y=0 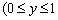
Вычисление: Построим график функций, которые ограничивают искомую площадь фигуры:
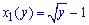
Выпишем пределы интегрирования:
y1=0; y2=1 (известно за условием).
График функций приведен ниже

Неизвестную площадь фигуры вычисляем интегрированием (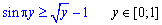
Пример 2.99 Вычислить площадь фигуры, ограниченной кривыми y=sin(x), y=cos(x), y=0 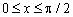
Вычисление: Из рисунку видно, что площадь S лучше разбить на две части: S=S1+S2.
Запишем уравнение функций, которые ограничивают искомую площадь фигуры:
Интегрируем синус и косинус функции и находим площадь.
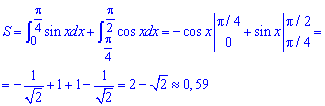
Второй вариант заключается в интегрировании разницы обратных функций по y.
Пример 2407 Найти площадь фигуры, ограниченной кривыми 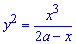
Вычисление: Поскольку график функции 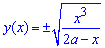
В точке x=2a функция не определена, поэтому будем иметь интеграл второго рода (детальнее смотрите часть ІІІ), он совпадает и, следовательно, площадь будет выражена числом.
Запишем пределы интегрирования:
x1=0 (потому что 
График функций следующий
Площадь фигуры, что ограниченна заданной кривой находится достаточно непростым интегрированием
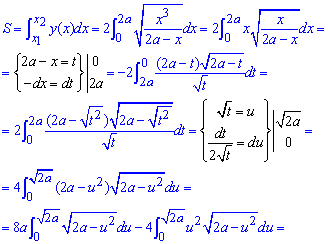
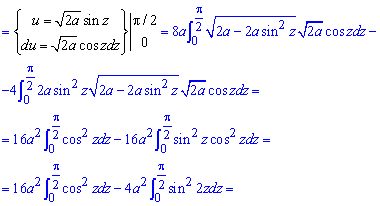
Здесь пришлось трижды выполнять замену переменных, чтобы прийти к правильному ответу.
Еще раз внимательно разберите интеграл.
Пример 2408 Вычислить площадь фигуры, ограниченной кривыми 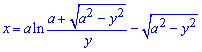
Вычисление: Трактриса — кривая, по которой двигается объект, когда его тянуть по горизонтальной плоскости за бечевку фиксированной длины, если направление движения тягача является ортогональным к начальному положению бечевки и скорость тягача бесконечно малая величина.
Очевидно, что 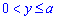

Принимая к сведению, что положительному приросту x отвечает отрицательный прирост y, и что фигура не квадрируема (в общем понимании), допускаем
где дифференциал за x находим через производную
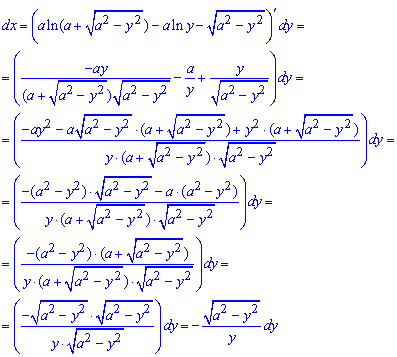
Площадь фигуры через определенный интеграл равна
Следующим идет материал из которого Вы научитесь находить площадь фигуры, ограниченной кривыми заданными параметрически.

 толькко если
толькко если  . В остальных случаях, как и указал
. В остальных случаях, как и указал  .
.
 подразумевается, видимо,
подразумевается, видимо,  имеет площадь
имеет площадь  под графиком от
под графиком от  до
до  , полученная растяжением вдоль оси
, полученная растяжением вдоль оси  в
в  раз и сжатием вдоль оси
раз и сжатием вдоль оси  в
в  . Зависимость легко угадать, проблема лишь в том, чтобы найти какую-нибудь одну синусоиду.
. Зависимость легко угадать, проблема лишь в том, чтобы найти какую-нибудь одну синусоиду.