{S_{полн} = 2(ab+bc+ac)}
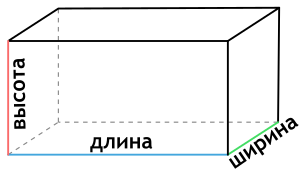
Чтобы найти площадь поверхности параллелепипеда необходимо знать длины трех его ребер. Для вычисления площади поверхности прямоугольного параллелепипеда используется формула, в которой сумма попарных произведений ребер параллелепипеда умножается на 2. По другому формулу можно трактовать как произведение площадей трех граней параллелепипеда (так как произведение ребер — это площадь грани). Кроме того на странице вы найдете калькулятор, с помощью которого в режиме онлайн можно найти площадь полной и боковой поверхности прямоугольного параллелепипеда.
В дополнение на сайте можно найти объем параллелепипеда.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
Ребро — сторона прямоугольного параллелепипеда. Длина, ширина и высота — это ребра прямоугольного параллелепипеда.
Содержание:
- калькулятор площади поверхности прямоугольного параллелепипеда
- формула площади поверхности прямоугольного параллелепипеда
- формула площади боковой поверхности прямоугольного параллелепипеда
- примеры задач
Формула площади поверхности прямоугольного параллелепипеда
{S_{полн} = 2(ab+bc+ac)}
a — длина прямоугольного параллелепипеда
b — ширина прямоугольного параллелепипеда
c — высота прямоугольного параллелепипеда
Формула площади боковой поверхности прямоугольного параллелепипеда
{S_{бок} = 2(ac+bc)}
a — длина прямоугольного параллелепипеда
b — ширина прямоугольного параллелепипеда
c — высота прямоугольного параллелепипеда
Примеры задач на нахождение площади поверхности прямоугольного параллелепипеда
Задача 1
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 2 4 и 5.
Решение
Для нахождения площади поверхности воспользуемся первой формулой. Подставим в нее значения длины, ширины и высоты параллелепипеда и произведем вычисления.
S_{полн} = 2(ab+bc+ac) = 2(2 cdot 4 + 4 cdot 5 + 2 cdot 5) = 2(8 + 20 + 10) = 2(38) = 76 : см^2
Ответ: 76 см²
Проверим ответ с помощью калькулятора .
Задача 2
Найдите площадь поверхности прямоугольного параллелепипеда, если его измерения равны 3см 5см и 6см.
Решение
Задача аналогична предыдущей, поэтому повторим действия, подставив новые значения измерений параллелепипеда.
S_{полн} = 2(ab+bc+ac) = 2(3 cdot 5 + 5 cdot 6 + 3 cdot 6) = 2(15 + 30 + 18) = 2(63) = 126 : см^2
Ответ: 126 см²
Для проверки ответа используем калькулятор .
Задача 3
Найдите площадь поверхности прямоугольного параллелепипеда измерения которого равны 9м 24м 11м.
Решение
Еще одна типовая задача. Для ее решения также воспользуемся первой формулой.
S_{полн} = 2(ab+bc+ac) = 2(9 cdot 24 + 24 cdot 11 + 9 cdot 11) = 2(216 + 264 + 99) = 2(579) = 1158 : см^2
Ответ: 1158 см²
Проверка .
Задача 4
Найдите площадь боковой поверхности прямоугольного параллелепипеда у которого a=4см, b=5см, c=7см.
Решение
В этой задаче нам необхожимо найти площадь боковой поверхности. Поэтому мы будем использовать для ее решения вторую формулу.
S_{бок} = 2(ac+bc) = 2(4 cdot 7 + 5 cdot 7) = 2(28 + 35) = 2(63) = 126 : см^2
Ответ: 126 см²
Как всегда ответ можно проверить с помощью калькулятора .
В данной публикации мы рассмотрим, как можно вычислить площадь поверхности прямоугольного параллелепипеда и разберем пример решения задачи для закрепления материала.
- Формула вычисления площади
- Пример задачи
Формула вычисления площади
Площадь (S) поверхности прямоугольного параллелепипеда вычисляется следующим образом:
S = 2 (ab + bc + ac)
Формула получена следующим образом:
- Гранями прямоугольного параллелепипеда являются прямоугольники, причем противоположные грани равны между собой:
- два основания: со сторонами a и b;
- четыре боковые грани: со стороной a/b и высотой c.
- Сложив площади всех граней, каждая из которых равна произведению сторон разной длины, получаем: S = ab + ab + bc + bc + ac + ac = 2 (ab + bc + ac).
Пример задачи
Вычислите площадь поверхности прямоугольного параллелепипеда, если известно, что его длина равна 6 см, ширина – 4 см, а высота – 7 см.
Решение:
Воспользуемся формулой выше, подставив в нее известные значения:
S = 2 ⋅ (6 см ⋅ 4 см + 6 см ⋅ 7 см + 4 см ⋅ 7 см) = 188 см2.
Как найти площадь поверхности параллелепипеда
На данной странице калькулятор поможет рассчитать площадь поверхности параллелепипеда онлайн. Для расчета задайте высоту, ширину и длину.
Прямоугольный параллелепипед – это многогранник, у которого все грани являются прямоугольниками.
Через стороны
a:
b:
c:
Результат
Ответы:
Формула площади поверхности параллелепипеда через его ребра:
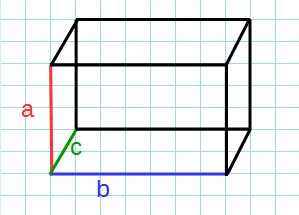
a, b, c — ребра параллелепипеда.
Прямоугольным параллелепипедом называется трехмерное тело, у которого противоположные грани параллельны и являются прямоугольниками. Проще говоря, прямоугольный параллелепипед представляет собой вытянутый куб.
Онлайн-калькулятор площади поверхности параллелепипеда
Прямоугольный параллелепипед можно охарактеризовать тремя числами — длинами его сторон: aa, bb, cc.
Формула площади поверхности параллелепипеда
Чтобы найти полную площадь поверхности параллелепипеда, нужно сложить площади всех его граней. Граней у параллелепипеда шесть, поэтому:
S=S1+S2+S3+S4+S5+S6S=S_1+S_2+S_3+S_4+S_5+S_6
Но так как противоположные грани прямоугольного параллелепипеда равны между собой, то: S1=S2S_1=S_2, S3=S4S_3=S_4, S5=S6S_5=S_6.
Поскольку гранями данного параллелепипеда являются прямоугольники, то их площади равны соответственно:
S1=S2=abS_1=S_2=ab
S3=S4=bcS_3=S_4=bc
S5=S6=acS_5=S_6=ac
Итак, полная площадь поверхности параллелепипеда:
S=2(ab+bc+ac)S=2(ab+bc+ac)
Из этой формулы следует, что если a=b=ca=b=c, то получим: S=6a2S=6a^2. Это и есть формула для площади поверхности куба со стороной aa.
Найдите площадь поверхности прямоугольного параллелепипеда со сторонами 2 см.2text{ см.}, 4 см.4text{ см.}, 6 см.6text{ см.}
Решение
a=2a=2
b=4b=4
c=6c=6
S=2(ab+bc+ac)=2(2⋅4+4⋅6+2⋅6)=88 (см. кв.)S=2(ab+bc+ac)=2(2cdot4+4cdot6+2cdot6)=88text{ (см. кв.)}
Ответ: 88 см. кв.88text{ см. кв.}
Найдите площадь поверхности прямоугольного параллелепипеда высотой 3 см.3text{ см.}, в основании которого лежит квадрат со стороной 1 см.1text{ см.}
Решение
a=b=1a=b=1
c=3c=3
S=2(ab+bc+ac)=2(1+3+3)=14 (см. кв.)S=2(ab+bc+ac)=2(1+3+3)=14text{ (см. кв.)}
Ответ: 14 см. кв.14text{ см. кв.}
Не знаете, где заказать задачу по геометрии? Обратитесь к нашим экспертам в данной области!
Тест по теме «Площадь поверхности параллелепипеда»
Площадь поверхности параллелепипеда
Алик Беникович Айрапетян
Эксперт по предмету «Калькуляторы»
Задать вопрос автору статьи
На этой странице вы узнаете, как выглядят формулы для расчёта полной и боковой площади поверхности параллелепипеда. Также на страницу добавлен онлайн-калькулятор для расчёта площади прямоугольного параллелепипеда.
Определение 1
Параллелепипед является разновидностью призмы, основания которой представляют собой параллелограммы. Также параллелепипедами называют призмы, в основании которых лежат многогранники, а все грани являются параллелограммами.
Наиболее знакомый всем вид параллелепипеда — это прямоугольный параллелепипед. Все его грани являются прямоугольниками.
Для расчёта полной площади прямоугольного параллелепипеда введите значение сторон и высоты в поля для ввода.
Площадь поверхности параллелепипеда через стороны
Для прямоугольного параллелепипеда площадь поверхности определяется по формуле:
$S = 2 cdot (a cdot b + b cdot h + a cdot h)$, здесь
$a, b$ — стороны основания параллелепипеда;
$h$ — высота параллелепипеда.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Разберём пример на нахождение полной площади параллелепипеда.
Пример 1
Задача
Стороны основания прямоугольного параллелепипеда равны $a = 3$ см и $b = 7$ см, а его высота $h$ равна $4$ см. Чему равна полная площадь поверхности параллелепипеда?
Решение:
Воспользуемся вышеприведённой формулой:
$S = 2 cdot (3 cdot 4 + 7 cdot 4 + 3 cdot 7) = 122$ кв. см.
Результаты совпадают с решением онлайн-калькулятора, а значит, ответ найден верно.
Также используя следующий онлайн-калькулятор, вы сможете рассчитать площадь боковой поверхности прямоугольного параллелепипеда.
Площадь боковой поверхности прямоугольного параллелепипеда через стороны
Площадь боковой поверхности прямоугольного параллелепипеда определяется по формуле:
$S = 2 cdot h cdot (a + b)$, где
$h$ — длина ребра параллелепипеда;
$a, b$ — стороны основания.
Рассчитаем для примера площадь боковой поверхности для параллелепипеда из предыдущей задачи.
Пример 2
Задача
$a = 3$ см, $b = 7$ см, а высота $h = 4$ см. Чему равна боковая площадь поверхности прямоугольного параллелепипеда?
Решение:
$S_б = 2 cdot 4 cdot (3 + 7) = 80$ кв. см.
Решение соответствует решению, полученному с помощью онлайн-калькулятора, а значит, ответ правильный.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 18.06.2019