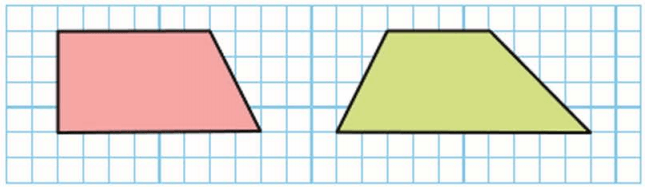
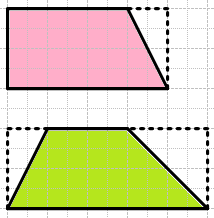
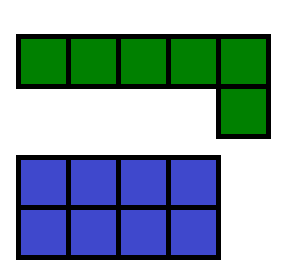
1) Начерти такие четырехугольники и дополни каждый из них до прямоугольника.
2) Найди площади полученных прямоугольников.
3) Найди периметр этих прямоугольников.
reshalka.com
ГДЗ учебник по математике 3 класс Моро. Часть 2. Страница 33. Номер №8
Решение 1
Решение 2
1) 2 * 4 = 8
(
с
м
2
)
− площадь красного прямоугольника;
2) 2 * 5 = 10
(
с
м
2
)
− площадь зеленого прямоугольника.
Ответ: 8
с
м
2
, 10
с
м
2
.
Решение 3
1) (2 + 4) * 2 = 6 * 2 = 12 (см) − периметр красного прямоугольника;
2) (2 + 5) * 2 = 7 * 2 = 14 (см) − периметр зеленого прямоугольника.
Ответ: 12 см, 14 см.
- Главная
- Справочник
- Как найти площадь прямоугольника
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Как найти площадь прямоугольника
Содержание:
- Формула
- Примеры вычисления площади прямоугольника
Формула
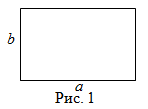
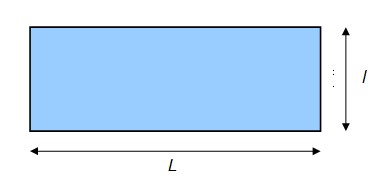
Чтобы найти площадь прямоугольника (рис. 1), надо его длину умножить на ширину, то есть
Прямоугольником называется четырехугольник, у которого все углы равны. Все углы в прямоугольнике прямые, то есть равны $90^{circ}$.
Примеры вычисления площади прямоугольника
Пример
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 см, а вторая, смежная с ней — 5 см.
Решение. Искомая площадь прямоугольника равна произведению двух заданных сторон:
$S=3 cdot 5=15$ (см2)
Ответ. $S=15$ (см2)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
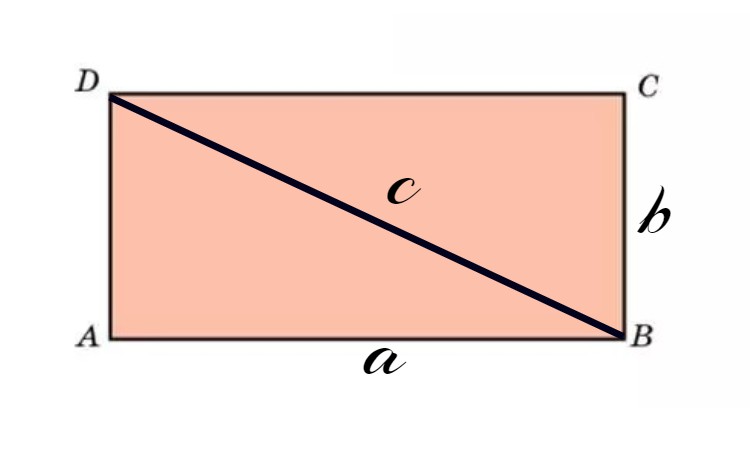
Задание. Найти площадь прямоугольника, если одна его сторона равна 3 м, а диагональ — 5 м.
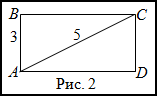
Решение. Сделаем чертеж (рис. 2).
Рассмотрим прямоугольный треугольник $ABC$, из которого по
теореме Пифагора найдем длину катета $BC$ :
$B C=sqrt{A C^{2}-A B^{2}}=sqrt{5^{2}-3^{2}}=sqrt{25-9}=sqrt{16}=4$ (м)
Тогда искомая площадь равна
$S=3 cdot 4=12$ (м2)
Ответ. $S=12$ (м2)
Читать дальше: как найти площадь параллелограмма.
Статьи по теме
- Как найти площадь
- Как найти площадь треугольника
- Как найти площадь ромба
- Как найти площадь эллипса
- Как найти площадь прямоугольного треугольника
- Все темы раздела «Как найти площадь»

Разделы
- Формулы сокращенного умножения
- Формулы по физике
- Логарифмы
- Векторы
- Матрицы
- Комплексные числа
- Пределы
- Производные
- Интегралы
- СЛАУ
- Числа
- Дроби
Все еще сложно?
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
250 ответов по вашей теме сегодня
2 специалиста свободны онлайн
Ответы приходят уже через 10 минут
90% ответов положительные
На чтение 5 мин. Просмотров 15.3k.
Площадь прямоугольника очень часто требуется найти в задачах по геометрии. И не только — в повседневной жизни очень многие плоскости имеют форму прямоугольника и надо найти площадь прямоугольника. Как это сделать? Давайте рассмотрим все формулы и примеры.
Мы учимся вычислять площадь прямоугольника или площадь прямоугольника в школе. Однако, когда вы станете старше, вполне возможно, что вы не будете помнить, как найти площадь прямоугольника. Для начала давайте вспомним, что такое прямоугольник.
Что такое прямоугольник
Давайте не будем «срезать углы». Чтобы иметь возможность вычислить площадь прямоугольника, естественно, что мы сначала знаем, что это такое. Поэтому для начала необходимо помнить, что прямоугольник является четырехугольником. Другими словами, это геометрическая фигура, которая имеет четыре стороны и четыре прямых угла. Противоположные стороны прямоугольника имеют одинаковую длину. Две самые длинные стороны представляют его длину, а две другие стороны представляют его ширину.
Не все четырехугольники являются прямоугольниками. Действительно, обязательно, чтобы они имели следующие свойства, чтобы мы могли сказать, что это действительно прямоугольник:
Характеристики прямоугольника
Противоположные стороны должны быть параллельны.
- Диагонали прямоугольника должны быть одинаковой длины. Они также пересекаются в своей середине.
- Точка пересечения диагоналей прямоугольника называется центром симметрии.
- Кроме того, прямоугольник также является параллелограммом, так как его стороны попарно параллельны. Однако это частный случай параллелограмма. На самом деле он имеет четыре прямых угла, и его две параллельные стороны не должны иметь одинаковую длину. В противном случае все четыре стороны имеют одинаковую длину — тогда мы говорим о квадрате.
Формула площади прямоугольника
Как рассчитать площадь прямоугольника? Обратите внимание, что базовую формулу для вычисления площади (или площади) прямоугольника очень легко запомнить. Вы просто должны умножить его длину на ширину.
Площадь прямоугольника равна его длине, умноженной на ширину.
Например, площадь прямоугольника длиной 4 сантиметра и шириной 2 сантиметра равна 4 x 2 = 8 см².
Найти площадь прямоугольника по известным длине и ширине — онлайн калькулятор.
Площадь прямоугольника:
Диагональ прямоугольника:
Площадь поверхности прямоугольника длиной L и шириной l равна: S = L x l
Принцип расчета площади прямоугольника
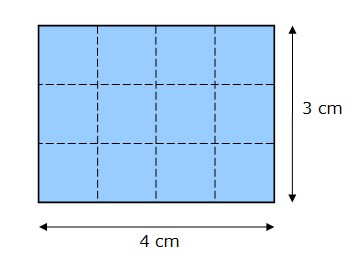
Чтобы вычислить площадь прямоугольника, мы посчитаем количество единиц областей, которые содержит прямоугольник:
В прямоугольнике выше 12 квадратов по 1 см². Его площадь составляет 12 см² (4 х 3).
Примечание. В этом расчете длина L и ширина l прямоугольника должны быть выражены в одной и той же единице длины. Результат будет выражен в той же единице измерения, возведенной в квадрат. Например, если длина прямоугольника выражена в метрах, ширина также должна быть выражена в метрах, а результат формулы для расчета площади прямоугольника даст результат в квадратных метрах (м²).
Площадь прямоугольника эквивалентна его территории. Территория — это термин, используемый для обозначения меры площади земли (мы используем единицу измерения гектар, а не м²). Гектар — это метрическая мера земельной площади, равная 10 000 м2.
Пример расчета
Рассмотрим прямоугольник длиной L = 4 см и шириной l = 2 см. Площадь S его поверхности равна:
A = L x l = 4 x 2 = 8 см².
Как рассчитать площадь прямоугольника, если мы знаем только одну сторону и диагональ
Можно определить площадь прямоугольника другим способом. Формула, которая была изложена ранее, не является единственным методом, который можно использовать. Действительно, вполне возможно сделать это по-другому. Для этого нам нужно будет, по крайней мере, измерить только одну сторону и необходимо знать длину диагонали. В этом случае мы делаем расчет, используя теорему Пифагора.
Что такое теорема Пифагора
Это формула, которая используется для определения длины третьей стороны прямоугольного треугольника, когда вы уже знаете значение двух других его сторон.
Обратите внимание, что прямоугольник состоит из двух прямоугольных треугольников. Действительно, диагональ представляет гипотенузу этого типа треугольника.
Кроме того, это также самая длинная сторона, которую можно найти на рисунке. Длина и ширина, с другой стороны, представляют две другие его стороны (скажем, смежные стороны). Это причина, почему можно использовать эту формулу для определения площади прямоугольника.
Теорема Пифагора основана на довольно простом уравнении, которое выглядит следующим образом: a² + b² = c². Где a и b используются для представления двух соседних сторон — катетов прямоугольного треугольника, а c представляет гипотенузу треугольника.
Чтобы полностью понять использование этой формулы, мы начнем с очень конкретного примера. Для этого предположим, что диагональ прямоугольника 10 см, а другая сторона 6 см. Если мы ссылаемся на формулу a² + b² = c², следовательно, сторона «a» составляет 6 см, а гипотенуза «c» — 10 см. Теперь нам нужно просто заменить буквенные значения числовыми значениями, которые у нас есть. Что дает нам:
a² + b² = c²
6² + b² = 10²
b² = 10² — 6²
b² = 100 — 36
b² = 64
b= 8
Мы получаем длину смежной стороны прямоугольника «b», которая равна 8 см. Теперь мы можем рассчитать площадь прямоугольника:
S = 8 см х 6 см
Следовательно, S = 48 см².
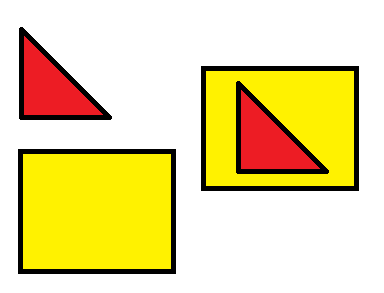
Сравнить площади разных фигур можно способом наложения. Посмотрите на рисунок. Мы видим две фигуры: треугольник и прямоугольник. Для того, чтобы их сравнить мы можем наложить меньшую фигуру на большую. Треугольник полностью поместился в прямоугольнике, это значит, что треугольник меньше прямоугольника.
Но не всегда можно сравнить площади фигур таким способом. Тогда можно разбить фигуру на равные квадраты и посчитать количество квадратов входящих в эту фигуру.
Площадь фигуры равна числу единичных квадратов, составляющих эту фигуру.
Если у квадрата сторона равна 1 см, то площадь такого квадрата равна 1 квадратному сантиметру (см2).
Площадь квадрата сторона которого равна 1 дециметр равна 1 квадратному дециметру (дм2) или 100 квадратным сантиметрам(см2).
Площадь фигуры обозначается заглавной латинской буквой S.
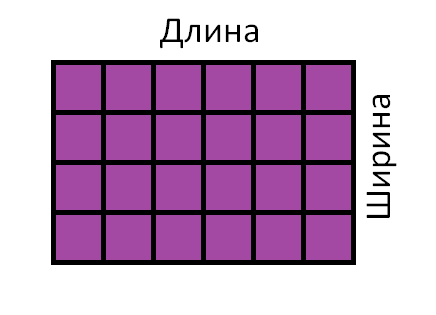
Итак, умножим длину прямоугольника на его ширину и получим площадь:
S = 6 × 4 = 24 см2
Чтобы вычислить площадь прямоугольника, надо измерить его длину и ширину в одинаковых единицах измерения и найти их произведение.
Если известна площадь прямоугольника и ширина, то найти длину просто, надо разделить площадь на известную длину.
Д = S ÷ Ш
или
Ш = S ÷ Д
Например, площадь прямоугольника равна 15 см2. Длина прямоугольника равна 5 см. Найдем его ширину:
Ш = 15 ÷ 5 = 3 см
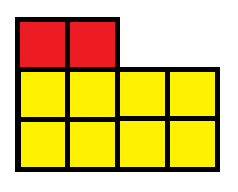
Итак нашу фигуру мы можем разбить на два прямоугольника: первый площадью 2 см2, и второй площадью 8 см2:
S = 2 × 1 + 4 × 2 = 10 см2
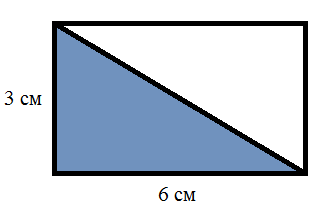
Теперь найдем площадь полученного прямоугольника и разделим её пополам:
S = (3 × 6) ÷ 2 = 9 см2
Кажется все просто, когда треугольник прямоугольный. Если у треугольника нет прямого угла, то вычислить его площадь можно следующим образом:
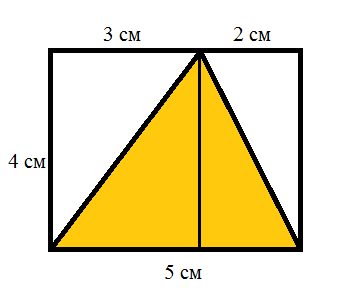
Теперь для того, чтобы найти площадь нашего треугольника, надо вычислить площади двух полученных прямоугольных треугольников и сложить их:
S1 = (3 × 4) ÷ 2 = 6 см2
S2 = (2 × 4) ÷ 2 = 4 см2
S = S1 + S2 = 6 + 4 = 10 см2
Спасибо, что Вы с нами.
Понравилась статья — поделитесь с друзьями:
Оставляйте пожалуйста комментарии в форме ниже
При подготовке к основному государственному экзамену я встретился с заданиями, в которых требуется вычислить площадь фигуры, изображенной на клетчатом листе бумаги. Как правило, эти задания не вызывают больших затруднений, если фигура представляет собой трапецию, параллелограмм или треугольник. Достаточно хорошо знать формулы вычисления площадей этих фигур, посчитать количество клеточек и вычислить площадь. Если фигура представляет собой некоторый произвольный многоугольник, то здесь необходимо использовать особые приемы. Меня заинтересовала данная тема. И естественно возникли вопросы: где в повседневной жизни могут возникнуть задачи на вычисление площадей на клетчатой бумаге? В чем особенность таких задач? Существуют ли другие методы или же универсальная формула для вычисления площадей геометрических фигур, изображенных на клетчатой бумаге?
Изучение специальной литературы и интернет источников, показало, что существует универсальная формула, позволяющая вычислить площадь фигуры, изображенной на клетке. Эта формула называется формулой Пика. Однако, в рамках школьной программы данная формула не рассматривается, несмотря на свою простоту в применении и получении результата. Более того, мною проведен опрос друзей и одноклассников (в двух формах: при личной беседе и в социальных сетях), в котором приняли участие 43 учащихся школ города Тобольска. Данный опрос показал, что всего один человек (учащийся 11 класса) знаком с формулой Пика для вычисления площадей.
Пусть задана прямоугольная система координат. В этой системе рассмотрим многоугольник, который имеет целочисленные координаты. В учебной литературе точки с целочисленными координатами называются узлами. Причем многоугольник не обязательно должен быть выпуклым. И пусть требуется определить его площадь.
Возможны следующие случаи.
1. Фигура представляет собой треугольник, параллелограмм, трапецию:
1) подсчитывая клеточки нужно найти высоту, диагонали или стороны, которые требуются для вычисления площади;
2) подставить найденные величины в формулу площади.
Например, требуется вычислить площадь фигуры, изображенной на рисунке 1 с размером клетки 1см на 1 см.

Рис. 1. Треугольник
Решение. Подсчитываем клеточки и находим: . По формуле получаем:
.
2 Фигура представляет собой многоугольник
Если фигура представляет собой многоугольник то возможно использовать следующие методы.
Метод разбиения:
1) разбить многоугольник на треугольники, прямоугольники;
2) вычислить площади полученных фигур;
3) найти сумму всех площадей полученных фигур.
Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см методом разбиения.

Рис. 2. Многоугольник
Решение. Способов разбиения существует множество. Мы разобьем фигуру на прямоугольные треугольники и прямоугольник как показано на рисунке 3.
Рис. 3. Многоугольник. Метод разбиения
Площади треугольников равны: ,
,
, площадь прямоугольника —
. Складывая площади всех фигур получим:
Метод дополнительного построения
1) достроить фигуру до прямоугольника
2) найти площади полученных дополнительных фигур и площадь самого прямоугольника
3) из площади прямоугольника вычесть площади всех «лишних» фигур.
Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см методом дополнительного построения.
Решение. Достроим нашу фигуру до прямоугольника как показано на рисунке 4.

Рис. 4. Многоугольник. Метод дополнения
Площадь большого прямоугольника равна , прямоугольника, расположенного внутри —
, площади «лишних» треугольников —
,
, тогда площадь искомой фигуры
.
При вычислении площадей многоугольников на клетчатой бумаге возможно использовать еще один метод, который носит название формула Пика по фамилии ученого ее открывшего.
Формула Пика
Пусть у многоугольника, изображённого на клетчатой бумаге только целочисленные вершины. Точки у которых обе координаты целые называются узлами решетки. Причем, многоугольник может быть как выпуклым, так и невыпуклым.
Площадь многоугольника с целочисленными вершинами равна , где B — количество целочисленных точек внутри многоугольника, а Г — количество целочисленных точек на границе многоугольника.
Например, для многоугольника, изображенного на рисунке 5.

Рис. 5. Узлы в формуле Пика
Например, требуется вычислить площадь фигуры, изображенной на рисунке 2 с размером клетки 1см на 1 см по формуле Пика.

Рис. 6. Многоугольник. Формула Пика
Решение. По рисунку 6: В=9, Г=10, тогда по формуле Пика имеем:
Ниже приведены примеры некоторых задач, разработанных автором на вычисление площадей фигур, изображенных на клетчатой бумаге.
1. В детском саду дети сделали аппликации родителям в подарок (рис.7). Найдите площадь аппликации. Размер каждой клетки равен 1см 1см.

Рис. 7. Условие задачи 1
2. Один гектар еловых насаждений может задерживать в год до 32 т пыли, сосновых — до 35 т, вяза — до 43 т, дуба — до 50 т. бука — до 68 т. Посчитайте, сколько тонн пыли задержит ельник за 5 лет. План ельника изображен на рисунке 8 (масштаб 1 см. — 200 м.).

Рис. 8. Условие задачи 2
3. В орнаментах хантов и манси, преобладают геометрические мотивы. Часто встречаются стилизованные изображения животных. На рисунке 9 изображен фрагмент мансийского орнамента «Заячьи ушки». Вычислите площадь закрашенной части орнамента.
|
|
|
Рис. 9. Условие задачи 3
4. Требуется покрасить стену заводского здания (рис. 10). Рассчитайте требуемое количество водоэмульсионной краски (в литрах). Расход краски: 1 литр на 7 кв. метров Масштаб 1см — 5м.
Рис. 10. Условие задачи 4
5. Звездчатый многоугольник — плоская геометрическая фигура, составленная из треугольных лучей, исходящих из общего центра, сливающихся в точке схождения. Особого внимания заслуживает пятиконечная звезда — пентаграмма. Пентаграмма — это символ совершенства, ума, мудрости и красоты. Это простейшая форма звезды, которую можно изобразить одним росчерком пера, ни разу не оторвав его от бумаги и при этом ни разу же не пройдя дважды по одной и той же линии. Нарисуйте пятиконечную звездочку не отрывая карандаша от листа клетчатой бумаги, так, чтобы все углы получившегося многоугольника находились в узлах клетки. Вычислите площадь полученной фигуры.
Проанализировав математическую литературу и разобрав большое количество примеров по теме исследования, я пришел к выводу, что выбор метода вычисления площади фигуры на клетчатой бумаге зависит от формы фигуры. Если фигура представляет собой треугольник, прямоугольник, параллелограмм или трапецию, то удобно воспользоваться всем известными формулами для вычисления площадей. Если фигура представляет собой выпуклый многоугольник, то возможно использовать как метод разбиения, так и дополнения (в большинстве случаях удобнее — метод дополнения). Если фигура представляет собой невыпуклый или звездчатый многоугольник, то удобнее применить формулу Пика.
Поскольку формула Пика является универсальной формулой для вычисления площадей (если вершины многоугольника находятся в узлах решетки), то ее можно использовать для любой фигуры. Однако, если многоугольник занимает достаточно большую площадь (или клетки мелкие), то велика вероятность допустить ошибку в подсчетах узлов решетки. Вообще, в ходе исследования, я пришел к выводу, что при решении подобных задач в ОГЭ лучше воспользоваться традиционными методами (разбиения или дополнения), а результат проверить по формуле Пика.
Литература:
- Вавилов В. В., Устинов А. В. Многоугольники на решетках. — М.: МЦНМО, 2006. — 72 с.
- Васильев И. Н. Вокруг формулы Пика// Научно-популярный физико-математический журнал «Квант». — 1974. — № 12. Режим доступа: http://kvant.mccme.ru/1974/12/vokrug_formuly_pika.htm
- Жарковская Н., Рисс Е. Геометрия клетчатой бумаги. Формула Пика. // Первое сентября. Математика. — 2009. -№ 23. — с.24,25.
Основные термины (генерируются автоматически): формула Пика, клетчатая бумага, площадь фигуры, фигура, вычисление площадей, многоугольник, площадь, размер клетки, условие задачи, универсальная формула.