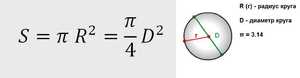
- Определение величины
- Область применения
- Способы расчета
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».
С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).
Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Способы расчета
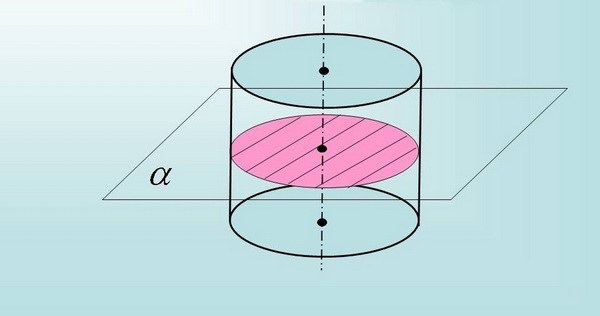
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
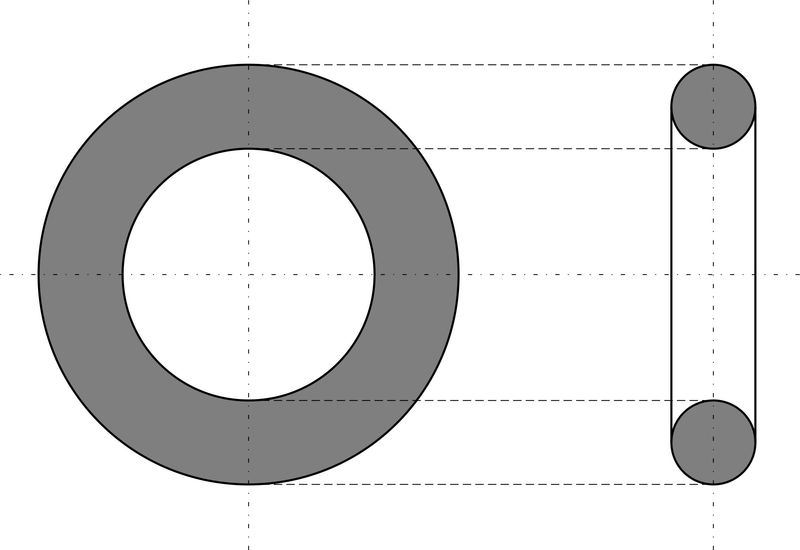
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:
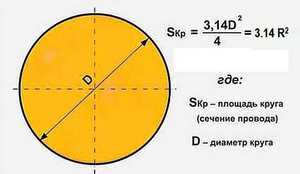
- Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
- Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
- Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.
Способов определения того, чему равна площадь круга, достаточно много. Чаще всего, если возникает подобная задача, на ум приходит знакомая еще со школьной скамьи формула «эс равно пи эр квадрат».
Как вычислить площадь поперечного сечения
Поперечное сечение образуется под прямым углом по отношению к продольной оси. Причем, сечение разных геометрических фигур представлено может быть различными формами. К примеру, у параллелограмма сечение по внешнему виду напоминает прямоугольник или квадрат, у цилиндра – прямоугольник или круг и т.д.
Вам понадобится
- — калькулятор;
- — исходные данные.
Инструкция
Чтобы найти площадь сечения параллелограмма, нужно знать значение его основания и высоту. Если, к примеру, известна лишь длина и ширина основания, то найдите диагональ, используя для этого теорему Пифагора (квадрат длины гипотенузы в прямоугольном треугольнике равен сумме квадратов катетов: a2 + b2 = c2). Ввиду этого, c = sqrt (a2 + b2).
Найдя значение диагонали, подставьте его в формулу S= c*h, где h – высота параллелограмма. Полученный результат и будет величиной площадью поперечного сечения параллелограмма.
Если же сечение проходит вдоль двух оснований, то его площадь рассчитывайте по формуле: S=a*b.
Для вычисления площади осевого сечения цилиндра, проходящей перпендикулярно основаниям (при условии, что одна сторона этого прямоугольника равна радиусу основания, а вторая – высоте цилиндра), используйте формулу S =2R*h, в которой R – величина радиуса окружности (основания), S – площадь поперечного сечения, а h – высота цилиндра.
Если по условиям задачи сечение не проходит через ось вращения цилиндра, но при этом параллельно его основаниям, значит, сторона прямоугольника не будет равна диаметру окружности основания.
Самостоятельно вычислите неизвестную сторону путем построения окружности основания цилиндра, проведения перпендикуляров от стороны прямоугольника (плоскости сечения) к окружности и расчета размера хорды (по теореме Пифагора). После этого подставьте в S =2а*h полученное значение (2а – значение хорды) и рассчитайте площадь поперечного сечения.
Площадь сечения шара определяется по формуле S = πR2. Обратите внимание на то, что, если расстояние от центра геометрической фигуры до плоскости будет совпадать с плоскостью, то площадь сечения равна будет нулю, потому как шар касается плоскости лишь в одной точке.
Обратите внимание
Дважды пересчитывайте полученный результат: так вы не допустите ошибки в расчетах.
Полезный совет
Чтобы рассчитать площадь сечения любой другой геометрической фигуры, воспользуйтесь математическим справочником, в котором подобраны формулы для расчета и даны подробные рекомендации.
Источники:
- Стереометрия. Теория
- поперечное сечение
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Расстояние от YY до самого дальнего волокна с учетом общего напряжения, когда нагрузка не лежит на плоскости
Идти
Расстояние от YY до самого дальнего волокна = (Общий стресс-((Осевая нагрузка/Площадь поперечного сечения)+((Эксцентриситет относительно главной оси XX*Осевая нагрузка*Расстояние от XX до самого дальнего волокна)/(Момент инерции относительно оси X))))*Момент инерции относительно оси Y/(Эксцентриситет относительно главной оси YY*Осевая нагрузка)
Площадь поперечного сечения с учетом общего напряжения — это место, где нагрузка не лежит на плоскости.
Идти
Площадь поперечного сечения = Осевая нагрузка/(стресс-(((Эксцентриситет относительно главной оси YY*Осевая нагрузка*Расстояние от YY до самого дальнего волокна)/(Момент инерции относительно оси Y))+((Эксцентриситет относительно главной оси XX*Осевая нагрузка*Расстояние от XX до самого дальнего волокна)/(Момент инерции относительно оси X))))
Расстояние от XX до самого дальнего волокна с учетом общего напряжения, когда нагрузка не лежит на плоскости
Идти
Расстояние от XX до самого дальнего волокна = ((стресс-((Осевая нагрузка/Площадь поперечного сечения)+(Эксцентриситет относительно главной оси YY*Осевая нагрузка*Расстояние от YY до самого дальнего волокна)/(Момент инерции относительно оси Y)))*Момент инерции относительно оси X)/(Осевая нагрузка*Эксцентриситет относительно главной оси XX)
Эксцентриситет относительно оси XX при заданном общем напряжении, где нагрузка не лежит на плоскости
Идти
Эксцентриситет относительно главной оси XX = ((стресс-(Осевая нагрузка/Площадь поперечного сечения)-((Эксцентриситет относительно главной оси YY*Осевая нагрузка*Расстояние от YY до самого дальнего волокна)/(Момент инерции относительно оси Y)))*Момент инерции относительно оси X)/(Осевая нагрузка*Расстояние от XX до самого дальнего волокна)
Общее напряжение при эксцентрической нагрузке, когда нагрузка не лежит на плоскости
Идти
стресс = (Осевая нагрузка/Площадь поперечного сечения)+((Эксцентриситет относительно главной оси YY*Осевая нагрузка*Расстояние от YY до самого дальнего волокна)/(Момент инерции относительно оси Y))+((Эксцентриситет относительно главной оси XX*Осевая нагрузка*Расстояние от XX до самого дальнего волокна)/(Момент инерции относительно оси X))
Эксцентриситет относительно оси YY при заданном общем напряжении, когда нагрузка не лежит на плоскости
Идти
Эксцентриситет относительно главной оси YY = ((стресс-(Осевая нагрузка/Площадь поперечного сечения)-(Эксцентриситет относительно главной оси XX*Осевая нагрузка*Расстояние от XX до самого дальнего волокна)/(Момент инерции относительно оси X))*Момент инерции относительно оси Y)/(Осевая нагрузка*Расстояние от YY до самого дальнего волокна)
Момент инерции относительно YY при заданном общем напряжении, когда нагрузка не лежит на плоскости
Идти
Момент инерции относительно оси Y = (Эксцентриситет относительно главной оси YY*Осевая нагрузка*Расстояние от YY до самого дальнего волокна)/(стресс-((Осевая нагрузка/Площадь поперечного сечения)+((Эксцентриситет относительно главной оси XX*Осевая нагрузка*Расстояние от XX до самого дальнего волокна)/Момент инерции относительно оси X)))
Момент инерции около XX при общем напряжении, когда нагрузка не лежит на плоскости
Идти
Момент инерции относительно оси X = (Эксцентриситет относительно главной оси XX*Осевая нагрузка*Расстояние от XX до самого дальнего волокна)/(стресс-((Осевая нагрузка/Площадь поперечного сечения)+((Эксцентриситет относительно главной оси YY*Осевая нагрузка*Расстояние от YY до самого дальнего волокна)/Момент инерции относительно оси Y)))
Расстояние от нейтральной оси до самого внешнего волокна с учетом общего единичного напряжения при внецентренной нагрузке
Идти
Расстояние до внешнего волокна = (Общее напряжение агрегата-(Осевая нагрузка/Площадь поперечного сечения))*Момент инерции относительно нейтральной оси/(Осевая нагрузка*Расстояние от приложенной нагрузки)
Момент инерции поперечного сечения при заданном суммарном единичном напряжении при внецентренной нагрузке
Идти
Момент инерции относительно нейтральной оси = (Осевая нагрузка*Расстояние до внешнего волокна*Расстояние от приложенной нагрузки)/(Общее напряжение агрегата-(Осевая нагрузка/Площадь поперечного сечения))
Площадь поперечного сечения при заданном суммарном единичном напряжении при внецентренной нагрузке
Идти
Площадь поперечного сечения = Осевая нагрузка/(Общее напряжение агрегата-((Осевая нагрузка*Расстояние до внешнего волокна*Расстояние от приложенной нагрузки/Момент инерции относительно нейтральной оси)))
Общее удельное напряжение при эксцентрической нагрузке
Идти
Общее напряжение агрегата = (Осевая нагрузка/Площадь поперечного сечения)+(Осевая нагрузка*Расстояние до внешнего волокна*Расстояние от приложенной нагрузки/Момент инерции относительно нейтральной оси)
Эксцентриситет при заданном отклонении при внецентренной нагрузке
Идти
Эксцентриситет нагрузки = (pi*(1-Осевая нагрузка/Критическая нагрузка на изгиб))*Прогиб при внецентренной нагрузке/(4*Осевая нагрузка/Критическая нагрузка на изгиб)
Прогиб при эксцентрической нагрузке
Идти
Прогиб колонны = (4*Эксцентриситет нагрузки*Осевая нагрузка/Критическая нагрузка на изгиб)/(pi*(1-Осевая нагрузка/Критическая нагрузка на изгиб))
Суммарное единичное напряжение при внецентренной нагрузке с учетом радиуса инерции
Идти
Общее напряжение агрегата = (Осевая нагрузка/Площадь поперечного сечения)*(1+(Расстояние до внешнего волокна*Расстояние от приложенной нагрузки/(Радиус вращения^2)))
Критическая нагрузка потери устойчивости при прогибе при внецентренной нагрузке
Идти
Критическая нагрузка на изгиб = (Осевая нагрузка*(4*Эксцентриситет нагрузки+pi*Прогиб колонны))/(Прогиб колонны*pi)
Нагрузка на прогиб при эксцентрической нагрузке
Идти
Осевая нагрузка = (Критическая нагрузка на изгиб*Прогиб колонны*pi)/(4*Эксцентриситет нагрузки+pi*Прогиб колонны)
Радиус вращения при эксцентрической нагрузке
Идти
Радиус вращения = sqrt(Момент инерции/Площадь поперечного сечения)
Площадь поперечного сечения с учетом радиуса инерции при внецентренной нагрузке
Идти
Площадь поперечного сечения = Момент инерции/(Радиус вращения^2)
Момент инерции при заданном радиусе вращения при внецентренной нагрузке
Идти
Момент инерции = (Радиус вращения^2)*Площадь поперечного сечения
Площадь поперечного сечения
При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений. Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:
S = πR2
При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.
Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:
a2 + b2 = c2
Из нее можно вывести такую формулу:
c = S*q*r*t*(a2 + b2)
Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:
S= c*h
S – площадь поперечного сечения, h это значений высоты параллелограмма. Результат, который получится после исчислений, будет означать площадь поперечного сечения. Такая формула:
S=a*b
используется в тех случаях, когда сечение идет параллельно двум основаниям.
При вычислении площади поперечного сечения цилиндра, которое проходит вдоль его оснований, если одна из сторон данного прямоугольника тождественна радиусу основания, а другая из сторон – высоте цилиндра используется такая формула:
S =2R*h
где h – высота цилиндра R – величина радиуса окружности. Если же сечение не проходит сквозь ось цилиндра и одновременно параллельно его основаниям, то это означает, что сторона данного треугольника не равняется диаметру окружности основания.
Для решения этой проблемы необходимо узнать значение неизвестной стороны предварительно нарисовав окружность у основания цилиндра. Расчет производится также по формуле выведенной из теоремы Пифагора. Затем подставляется формула:
S =2а*h
где 2а – значение хорды, расчета площади поперечного сечения.
Круг — это геометрическое место точек на плоскости, расстояние от которых до его центра, не превышает заданного числа, называемого радиусом этого круга.
Сечение круга — это изображение фигуры, образованной рассечением круга плоскостью в поперечном направлении.
Формула для расчета площади поперечного сечения круга:
S = π * d 2 / 4
, где
d — диаметр круга.
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета площади поперечного сечения круга, если известен диаметр круга. С помощью этого калькулятора вы в один клик сможете рассчитать площадь сечения круга.
При решении заданий сопротивления материалов в расчетные формулы вводят величины, которые определяют формулу и размеры поперечных сечений, они называются геометрическими характеристиками плоских сечений. Первой такой величиной стоит считать площадь сечения. Рассчитать площадь поперечного сечения можно даже ствола дерева, ведь оно по форме похоже на эллипс или круг. Согласно формуле, площадь поперечного сечения круга, возможно, рассчитать достаточно точно по формуле. Площадь сечения круга или шара можно найти по формуле:
S = πR 2
При этом не стоит забывать о том, что расстояние от плоскости до центра фигуры совпадет с плоскостью, тогда плоскость поперечного сечения шара будет равняться нулю, так как касание им плоскости происходит лишь в одной точке.
Рассмотрим на примере параллелограмма. Прежде всего, для того чтобы найти площадь поперечного сечения, необходимо знать значения высоты и снования параллелограмма. Даже если нам известна только ширина основания и его длина через эти значения возможно найти диагональ, используя теорему Пифагора: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Формула выглядит как:
a 2 + b 2 = c 2
Из нее можно вывести такую формулу:
c = S*q*r*t*(a 2 + b 2 )
Когда у нас известно значение диагонали параллелограмма, то его можно подставить в формулу:
Площадь поперечного сечения как электротехническая величина
В электротехнике площадь ПС будет значить прямоугольное сечение проводника в отношении к его продольной части. Сечение жил всегда будет круглым. Измерение параметра осуществляется в мм2.
Начинающие электрики могут перепутать диаметр и сечение элементов. Чтобы определить, какая площадь сечения у жилы, понадобиться учесть его круглую форму и воспользоваться формулой:
S = πхR2, где:
- S – площадь круга;
- π – постоянная величина 3,14;
- R – радиус круга.
Если известен показатель площади, легко найти удельное сопротивление материала изготовления и длину провода. Далее вычисляется сопротивление тока.
Для удобства расчетов начальная формула преобразуется:
- Радиус – это ½ диаметра.
- Для вычисления площади π умножается на D (диаметр), разделенный на 4, или 0,8 умножается на 2 диаметра.
При вычислениях используют показатель диаметра, поскольку его неправильный подбор может вызвать перегрев и воспламенение кабеля.
Таблица с формулами площади круга
| Радиус круга r |
| Диаметр
– это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно |
| исходные данные (активная ссылка для перехода к калькулятору) | эскиз | формула |
| 1 | радиус | |
| 2 | диаметр | |
| 3 | длина окружности | |
| 4 | сторона квадрата вписанного в круг | |
| 5 | сторона квадрата, в который вписан круг | |
| 6 | стороны треугольника | где |
| 7 | сторона равностороннего треугольника | |
| 8 | высота равностороннего треугольника | |
| 9 | боковая сторона и основание равнобедренного треугольника | |
| 10 | стороны при прямом угле треугольника | |
| 11 | боковая сторона и основание равнобедренного треугольника | |
| 12 | боковые стороны равнобедренного треугольника и угол между ними | |
| 13 | стороны прямоугольного треугольника | |
| 14 | сторона и угол при основании треугольника | |
| 15 | сторона равностороннего треугольника | |
| 16 | сторона и угол при основании трапеции | |
| 17 | боковые стороны и диагональ трапеции | где |
| 18 | стороны прямоугольника | |
| 19 | сторона и количество сторон многоугольника | |
| 20 | сторона шестиугольника |
Общая информация о кабеле и проводе
При работе с проводниками необходимо понимать их обозначение. Существуют провода и кабеля, которые отличаются друг от друга внутренним устройством и техническими характеристиками. Однако многие люди часто путают эти понятия.
Проводом является проводник, имеющий в своей конструкции одну проволоку или группу проволок, сплетенных между собой, и тонкий общий изоляционный слой. Кабелем же называется жила или группа жил, имеющих как собственную изоляцию, так и общий изоляционный слой (оболочку). Каждому из типов проводников будут соответствовать свои методы определения сечений, которые почти схожи.
Онлайн-калькулятор площади поверхности цилиндра
На самом деле, это определение только самого простого, кругового цилиндра. Более общее определение цилиндрического тела следующее:
Цилиндром называют тело, образованное пересечением параллельных друг другу прямых и двух плоских поверхностей.
Такие прямые называются образующими данного цилиндра. Прямая, перпендикулярная обоим основаниям, является высотой цилиндра. Плоские поверхности называют основаниями данного цилиндра. Часто, они параллельны друг другу, но не всегда.
Что значит поперечное сечение
Перед тем как раскрыть основное понятие, нужно расшифровать значение термина и понять, чем провод отличается от кабеля. Провод является проводником, который используется, чтобы соединить несколько участков электрической цепи. Может иметь одну или много токовых проводящих жильных элементов. Они в свою очередь могут быть голыми, изолированными, одножильными и многожильными.
Первые используются в воздушных линиях электрических передач. Вторые применяются в электрических устройствах, щитках или шкафах. В быту они находятся внутри электрической проводки.
К сведению! Изолированные и одножильные проводники используются везде, а многожильные применяются там, где нужны изгибы с малым радиусом.
Поперечным сечением называется фигура, которая образуется от проводникового рассечения плоскостью направления. Площадь, которая получена при перпендикулярном разрезе любого вида провода, указывается в квадратных миллиметрах. Это важный параметр для расчета электрической сети.
Сечение по ГОСТу или ТУ
Большой ассортимент электротехнических товаров способствует быстрому решению задач, которые связаны с электромонтажными работами. Качество этой продукции играет очень важную роль и все товары должны соответствовать требованиям ГОСТ.
Как итог – рынок перенасыщен некачественным и дешевым товаром, который требуется перепроверять перед покупкой.
Если имеющиеся в торговых точках кабели подходящей стоимости не соответствуют заявленным характеристикам, единственное что можно сделать – приобрести провод с запасом по поперечному сечению. Резерв мощности никогда отрицательно не скажется качестве электропроводки. Также будет нелишним обратить внимание на продукцию от производителей, дорожащих своим именем – хоть она и стоит дороже, но это гарантия качества, а замена проводки делается не так часто, чтобы на ней экономить.
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью.
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).
Теорема гласит: площадь круга (S) равна произведению половины длины окружности и его радиуса. Длина окружности С находится в прямой зависимости от радиуса R с коэффициентом π («пи» = 3,14).
Цели расчета
Рассчитывать параметры площади сечения проводника необходимо с несколькими целями:
- получение необходимого количества электричества для запитки бытовых приборов;
- исключение переплат за неиспользуемый энергоноситель;
- безопасность проводки и предотвращение возгораний;
- возможность подключения высокомощной техники к сети;
- предотвращение оплавления изоляционного слоя и коротких замыканий;
- правильная организация осветительной системы.
Оптимальное сечение провода для освещения – 1,5 мм2 для линии, 4-6 мм2 на вводе.
Допустимая плотность тока для медного провода
При создании сетей в современных объектах недвижимости предпочитают использовать именно такие проводники. При одинаковом сечении они меньше перегреваются, по сравнению с алюминиевыми аналогами. В многожильном исполнении медные кабели хорошо подходят для создания сетевых соединительных шнуров, удлинителей. Их можно использовать для создания поворотов с малым радиусом.
Тепловой нагрев
Для расчета количества тепла (Q), выделяемого проводником, пользуются формулой I*2*R*t, где:
- I – сила тока, в амперах;
- R – сопротивление одного метра медного проводника;
- t – время испытания в определенных условиях.
Рассеивание тепла при работе кабеля
Тонкие проводники эффективно отдают тепловую энергию окружающей среде. На процесс оказывают существенное влияние конкретные условия. Как отмечено выше, контакт оболочки с водой существенно улучшает охлаждение.
По мере увеличения сечения часть энергии расходуется для нагрева прилегающих слоев. Этим объясняется постепенное снижение допустимой плотности тока в расчете на единицу площади.
Распределение температур в кабельной продукции
На рисунке хорошо видно, как при уменьшении изоляционного слоя улучшается теплоотдача.
Падение напряжения
Этот параметр несложно рассчитать по закону Ома (U=R*I) с учетом электрического сопротивления соответствующего материала. Удельное значение для меди берут 0,0175 Ом *мм кв./ метр. С помощью формул вычисляют на участке определенной длины падение напряжения. При сечении 1,5 мм кв. на каждый метр потери составят 0,01117 Вольт.
Допустимая плотность тока
Этот относительный параметр показывает разрешенный нормативами ток на один мм кв. площади сечения. Отмеченные выше тенденции по изменению теплоотдачи при увеличении размеров проводника подтверждаются расчетами и данными лабораторных испытаний.
Таблица допустимых значений плотности тока для разных условий в медном проводнике
| Поперечное сечение, мм кв. | Ток (А)/ Плотность тока (А/ мм кв.) | |
| Для трассы в здании | Монтаж на открытом воздухе | |
| 6 | 73/ 12,2 | 76/ 12,6 |
| 10 | 103/ 10,3 | 108/ 10,8 |
| 25 | 165/ 6,6 | 205/ 8,2 |
| 50 | 265/ 5,3 | 335/ 6,7 |
Пути повышения допустимого тока
Существенное значение имеют действительные условия эксплуатации трассы электроснабжения, трансформаторов, установок. Снизить рассматриваемые нагрузки можно с помощью хорошей вентиляции, естественной или принудительной. Хороший отвод тепла получится с применением перфорированных металлических коробов, которые не затрудняют прохождение конвекционных потоков и одновременно выполняют функции радиатора.
В некоторых ситуациях пригодится квалифицированно составленный временной график. Стиральная машина при нагреве воды и в режиме сушки потребляет много электроэнергии. Ее можно настроить на автоматическое выполнение рабочих операций в ночные часы. Если снабжающие организации предлагают соответствующую тарификацию, получится дополнительная экономия денежных средств.
Вентилятор обеспечивает эффективное охлаждение проводников, которые установлены в микроволновой печи
Допустимый ток и сечение проводов
Лучшие показатели теплообмена при остальных равных условиях характерны для проводников с относительно меньшей площадью поперечного сечения.
Таблица токовых параметров для кабелей с медными жилами
| Сечение, мм кв. | Плотность тока, А/ мм кв. | Ток, А |
| 1 | 15 | 15 |
| 1,5 | 13,3 | 20 |
| 2,5 | 10,8 | 27 |
| 16 | 5,7 | 92 |
| 25 | 4,9 | 123 |
Расчет сечения многожильного проводника
- Находится показатель площади сечения у одной жилы.
- Пересчитываются кабельные жилы.
- Количество умножается на поперечное сечение одной жилы.
При подключении многожильного проводника его концы обжимаются специальной гильзой с использованием обжимных клещей.
Рассеяние пучков частиц
В часто встречающемся случае упругого рассеяния пучка частиц, движущихся с одинаковой скоростью, на некотором центре, используется дифференциальное эффективное поперечное сечение
(dσdΩ{displaystyle {dsigma /dOmega }}), характеризующее вероятность рассеяния в определённый телесный угол (dΩ{displaystyle dOmega }). Оно равно отношению числа частиц, рассеянных в единицу времени в единицу телесного угла, к плотности потока падающих частиц.
Интегрирование по полному телесному углу даёт полное поперечное сечение
, для рассеяния на любые углы:
σ=∫dσdΩdΩ{displaystyle sigma =int {dsigma over dOmega }dOmega }
При наличии неупругих взаимодействий полное сечение складывается из сечения для упругих и неупругих рассеяний. Для каждого типа (канала) неупругих взаимодействий может быть введено отдельное эффективное сечение.
В чем измеряется поперечное сечение
После определения диаметра указанными способами площадь сечения можно определить по формуле или специальной таблице. Измеряется она в квадратных миллиметрах. Данная единица измерения производная согласно единой международной системе измерений.
Вам это будет интересно Опасность напряжения шага
При этом разрез жил всегда круглый.
Особенности самостоятельного расчета
При помощи штангенциркуля
Способ оправдан, если будут измеряться параметры усеченного, или бракованного кабеля. К примеру, ВВГ может обозначаться как 3х2,5, но фактически быть 3х21. Вычисления производятся так:
- С проводника снимается изоляционное покрытие.
- Диаметр замеряется штангенциркулем. Понадобится расположить провод между ножками инструмента и посмотреть на обозначения шкалы. Целая величина находится сверху, десятичная – снизу.
- На основании формулы поиска площади круга S = π (D/2)2 или ее упрощенного варианта S = 0,8 D² определяется поперечное сечение.
- Диаметр равен 1,78 мм. Подставляя величину в выражение и округлив результат до сотых, получается 2,79 мм2.
Для бытовых целей понадобятся проводники с сечением 0,75; 1,5; 2,5 и 4 мм2.
С использованием линейки и карандаша
При отсутствии специального измерителя можно воспользоваться карандашом и линейкой. Операции выполняются с тестовым образом:
- Зачищается от изоляционного слоя участок, равный 5-10 см.
- Получившаяся проволока наматывается на карандаш. Полные витки укладываются плотно, пространства между ними быть не должно, «хвостики» направляются вверх или вниз.
- В конечном итоге должно получиться определенное число витков, их требуется посчитать.
- Намотка прикладывается к линейке так, чтобы нулевое деление совпадало с первой намоткой.
- Замеряется длина отрезка и делится на количество витков. Получившаяся величина – диаметр.
- Например, получилось 11 витков, которые занимают 7,5 мм. При делении 7,5 на 11 выходит 0,68 мм – диаметр кабеля. Сечение можно найти по формуле.
Точность вычислений определяется плотностью и длиной намотки.
Таблица соответствия диаметра проводов и площади их сечения
Если нет возможности пройти тестирование диаметра или сделать вычисление при покупке, допускается использовать таблицу. Данные можно сфотографировать, распечатать или переписать, а затем применять, чтобы найти нормативный или популярный размер жилы.
| Диаметр кабеля, мм | Сечение проводника, мм2 |
| 0,8 | 0,5 |
| 0,98 | 0,75 |
| 1,13 | 1 |
| 1,38 | 1,5 |
| 1,6 | 2 |
| 1,78 | 2,5 |
| 2,26 | 4 |
| 2,76 | 6 |
| 3,57 | 10 |
При покупке электрокабеля понадобится посмотреть параметры на этикетке. К примеру, используется ВВНГ 2х4. Количество жил – величина после «х». То есть, изделие состоит из двух элементов с поперечным сечением 4 мм2. На основании таблицы можно проверить точность информации.
Чаще всего диаметр кабеля меньше, чем заявлен на упаковке. У пользователя два варианта – применять другой или выбрать с большей площадью сечения кабель по диаметру. Выбрав второй, понадобится проверить изоляцию. Если она не сплошная, тонкая, разная по толщине, остановитесь на продукции другого изготовителя.
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a ее можно найти по теореме Пифагора: отсюда . После того, как найдем диагональ – мы сможем рассчитать радиус: . И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Рассмотрим пример расчета площади круга, описанного вокруг квадрата. Задача: дан квадрат, вписанный в круг. Его сторона a = 4 см. Найдите площадь окружности. Для начала рассчитаем длину диагонали d. Теперь подставляем данные в формулу
Зная несколько простых правил и теорему Пифагора, мы смогли рассчитать площадь описанной вокруг квадрата окружности.