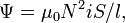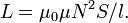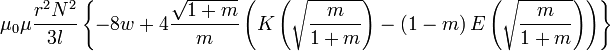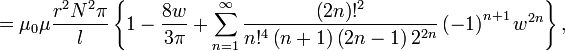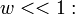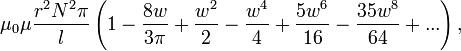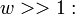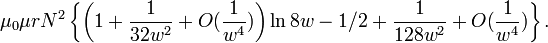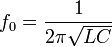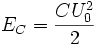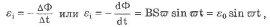Как найти площадь поперечного сечения соленоида - Исправление недочетов и поиск решений вместе с Examum.ru

Окей, остальные задачки:

1) Магнитное поле в центре кругового витка вычисляется по формуле B = μₒI/2R, откуда по известной индукции и известному радиусу враз находится величина тока. Плотность тока — это ток делить на площадь сечения проводника. Площадь сумеете сосчитать?

2) Индуктивность соленоида можно выразить не только через его длину и число витков (как у Габбаса), но и через длину намотки (l) и плотность намотки (n): L = μₒn²lS. Слова «из прилегающих вплотную» как раз и дают плотность намотки — не забудьте выразить её в числе витков на метр. Индуктивность и магнитный поток Ф внутри соленоида связаны простым соотношением Ф = IL, a индукция через магнитный поток — как B = ФS. Стало быть, индукция магнитного поля внутри соленоида связана с током как B = ILS, При этом площадь сечения соленоида равна πr² (r — тот самый радиус, который надо найти). Отсюда ток I = B/LS = B/Lπr².

В свою очередь, ток, по закону Ома, равен U/R, a R = ρl/s (l — длина проводника, s — его сечение). Полная длина проводника тут — это число витков умножить на длину одного витка, а длина одного витка = 2πr. Число витков N известно, поскольку длина соленоида и шаг витков в задачке указаны. Значит, ток от радиуса зависит как I = U/R = U/(ρl/s) = U/(ρN*2πr/s).

Приравнивая два выражения для тока друг к другу, можно найти радиус.

4) Полное индуктивное сопротивление Z = R + jωL + 1/jωC = R+j(ωL-1/ωC). Из этой формуле можно получить и выражение для его модуля — уж потрудитесь сделать это самостоятельно. Оный же модуль вычисляется из условия задачки по тому же закону Ома. И если приравнять два полученных модуля друг другу, то получится уравнение относительно L. Не штука.

Источник

Содержание

Площадь поперечного сечения соленоида это
Индуктивность соленоида
Более точные формулы для соленоида конечного размера
Принцип действия

Площадь поперечного сечения соленоида это

Площадь поперечного сечения соленоида с железным сердечником S = 10 см 2 ; длина соленоида ℓ = 1 м. Найти магнитную проницаемость μ материала сердечника, если магнитный поток, пронизывающий поперечное сечение соленоида, Ф = 1,4 мВб. Какому току I, текущему через соленоид, соответствует этот магнитный поток, если известно, что индуктивность соленоида при этих условиях L = 0,44 Гн?

Магнитный поток, пронизывающий соленоид

Откуда магнитная индукция

По графику зависимости В(Н) находим значение Н, соответствующее

Тогда магнитная проницаемость железа

Напряженность поля соленоида

Искомое значение силы тока

Ответ:

Источник

Индуктивность соленоида

Соленоид — длинная, тонкая катушка, то есть катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках здесь подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного материала плотность магнитного потока 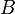внутри катушки является фактически постоянной и (приближенно) равна

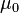
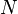
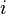
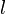
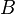
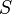
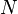
где − магнитная постоянная, − число витков, − ток и − длина катушки. Пренебрегая краевыми эффектами на концах соленоида, получим [16] , что потокосцепление через катушку равно плотности потока , умноженному на площадь поперечного сечения и число витков :

Отсюда следует формула для индуктивности соленоида (без сердечника):

Если катушка внутри полностью заполнена магнитным материалом (сердечником), то индуктивность отличается на множитель 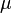— относительную магнитную проницаемость [17] сердечника:

В случае, когда , можно (следует) под S понимать площадь сечения сердечника и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз.

Более точные формулы для соленоида конечного размера

Для однослойного (с очень тонкой намоткой) соленоида конечных размеров (не бесконечно длинного) существуют более точные, хотя и более сложные формулы [18] :

— количество витков,

— радиус цилиндра,

— длина его образующей,

— Эллиптические интегралы.

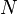
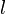
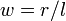
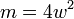
для

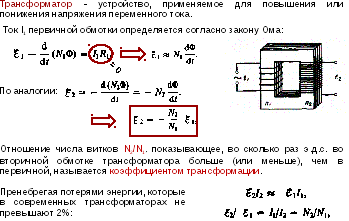
Трансформатор. Энергия магнитного поля. Основы теории Максвелла. Уравнения Максвелла в интегральной форме.

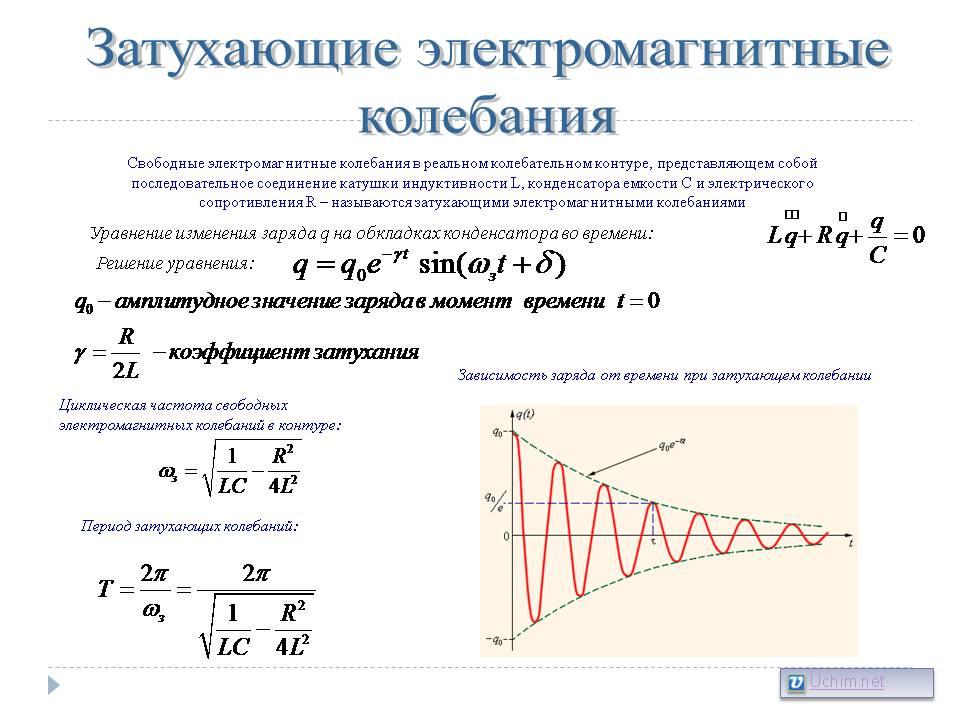
Электрический колебательный контур. Затухающие электромагнитные колебания. Вынужденные электромагнитные колебания. Явление резонанса

Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).

Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания

Резонансная частота контура определяется так называемой формулой Томсона:

Принцип действия

Пусть конденсатор ёмкостью C заряжен до напряжения 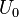. Энергия, запасённая в конденсаторе составляет

При соединении конденсатора с катушкой индуктивности, в цепи потечёт ток 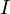, что вызовет в катушке электродвижущую силу (ЭДС) самоиндукции, направленную на уменьшение тока в цепи. Ток, вызванный этой ЭДС (при отсутствии потерь в индуктивности) в начальный момент будет равен току разряда конденсатора, то есть результирующий ток будет равен нулю. Магнитная энергия катушки в этот (начальный) момент равна нулю.

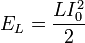
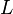
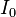
Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора . Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна

, где — индуктивность катушки, — максимальное значение тока.

После этого начнётся перезарядка конденсатора, то есть заряд конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор, в этом случае, снова будет заряжен до напряжения .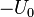

В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.

В общем, описанные выше процессы в параллельном колебательном контуре называются резонанс токов, что означает, что через индуктивность и ёмкость протекают токи, больше тока проходящего через весь контур, причем эти токи больше в определённое число раз, которое называется добротностью. Эти большие токи не покидают пределов контура, так как они противофазны и сами себя компенсируют. Стоит также заметить, что сопротивление параллельного колебательного контура на резонансной частоте стремится к бесконечности (в отличие от последовательного колебательного контура, сопротивление которого на резонансной частоте стремится к нулю), а это делает его незаменимым фильтром.

Стоит заметить, что помимо простого колебательного контура, есть ещё колебательные контуры первого, второго и третьего рода, что учитывают потери и имеют другие особенности.

Вынужденными электромагнитными колебаниями называют периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием переменной ЭДС от внешнего источника. Внешним источником ЭДС в электрических цепях являются генераторы переменного тока, работающие на электростанциях.

Принцип действия генератора переменного тока легко показать при рассмотрении вращающейся рамки провода в магнитном поле.

В однородное магнитное поле с индукцией В помещаем прямоугольную рамку, образованную проводниками (abсd).

Пусть плоскость рамки перпендикулярна индукции магнитного поля В и ее площадь равна S.

Магнитный поток в момент времени t₀ = 0 будет равен Ф = В*8.

При равномерном вращении рамки вокруг оси OO₁ с угловой скоростью w магнитный поток, пронизывающий рамку, будет изменяться с течением времени по закону:

Изменение магнитного потока возбуждает в рамке ЭДС индукцию, равную

где Е₀= ВSw — амплитуда ЭДС.

Если с помощью контактных колец и скользящих по ним щеток соединить концы рамки с электрической цепью, то под действием ЭДС индукции, изменяющейся со временем по гармоническому закону, в электрической цепи возникнут вынужденные гармонические колебания силы тока — переменный ток.

На практике синусоидальная ЭДС возбуждается не путем вращения рамки в магнитном поле, а путем вращения магнита или электромагнита (ротора) внутри статора — неподвижных обмоток, навитых на сердечники из магнитомягкого материала. В этих обмотках находится переменная ЭДС, что позволяет избежать снятия напряжения с помощью контактных колец.

Явление резонанса относится к наиболее важным с практической точки зрения свойствам электрических цепей. Оно заключается в том, что электрическая цепь, имеющая реактивные элементы обладает чисто резистивным сопротивлением.

Общее условие резонанса для любого двухполюсника можно сформулировать в виде Im[Z]=0 или Im[Y]=0, где Z и Y комплексное сопротивление и проводимость двухполюсника. Следовательно, режим резонанса полностью определяется параметрами электрической цепи и не зависит от внешнего воздействия на нее со стороны источников электрической энергии.

Источник

Тема: Определить число витков соленоида (Прочитано 23537 раз)

0 Пользователей и 1 Гость просматривают эту тему.

Галина Валерьевна

Здравствуйте срочно нужна помощь в решении. Заранее огромное спасибо

Индуктивность L соленоида, намотанного в один слой на каркас с магнитной проницаемостью µ= 250, равна 0,5 мГн. Длина соленоида l = 0,4 м, диаметр D = 1,5 см. Определить число витков соленоида.

Записан

Kivir

Решение: индуктивность соленоида (катушки, намотанной в один слой), можно определить по формуле:
[ L=mu cdot mu _{0} cdot frac{N^{2} cdot S}{l}, ]
здесь: N — число витков, S — площадь сечения, l — длина катушки, μ – относительная магнитная проницаемость среды заполняющей катушку, μ₀ = 4π∙10^–7 Гн/м – магнитная постоянная. Площадь сечения соленоида определим как площадь круга:
[ S=frac{pi cdot D^{2}}{4}. ]
Подставим в формулу индуктивности, и выразим число витков:
[ begin{array}{l} {L=mu cdot mu _{0} cdot frac{N^{2} cdot pi cdot D^{2} }{lcdot 4} ,} \ {N=sqrt{frac{4cdot lcdot L}{mu cdot mu _{0} cdot pi cdot D^{2}}}.}end{array} ]
Ответ: 60 витков

Записан

Дмирий

Что вы помогаете.У меня подобная задача была. Теперь вижу,что решил правильно

Записан

Галина Валерьевна

Спасибо за решение. Оказывается всё так просто, если учитывать площадь сечения соленоида(как площадь круга).

Записан

Источник

Классическая электродинамика

Магнитное поле соленоида

Электричество · Магнетизм

Электростатика
Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал

Магнитостатика
Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток

Электродинамика

Диполь
Потенциалы Лиенара — Вихерта
Сила Лоренца
Ток смещения
Униполярная индукция
Уравнения Максвелла
Электрический ток
Электродвижущая сила
Электромагнитная индукция
Электромагнитное излучение
Электромагнитное поле

Электрическая цепь
Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс

Ковариантная формулировка
Тензор электромагнитного поля Тензор энергии-импульса 4-ток · 4-потенциал

Известные учёные
Генри Кавендиш Майкл Фарадей Андре-Мари Ампер Густав Роберт Кирхгоф Джеймс Клерк (Кларк) Максвелл Генри Рудольф Герц Альберт Абрахам Майкельсон Роберт Эндрюс Милликен

См. также: Портал:Физика

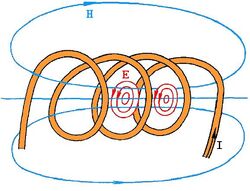
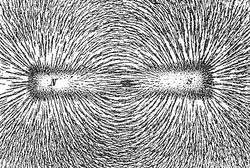
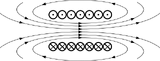
Рис. 1. Соленоид с однослойной намоткой.

Образование магнитного потока в соленоиде. В центре по длине на оси соленоида магнитное поле практически однородно.

Схема магнитных и вихревых электрических полей в соленоиде при протекании по обмотке переменного тока.

Рис.2. Картина силовых линий магнитного поля, создаваемого постоянным магнитом в форме стержня. Железные опилки на листе бумаги.

Солено́ид — (греч. solen — канал, и eidos — подобный) разновиднось катушки индуктивности. Обычно под термином «соленоид» подразумевается цилиндрическая обмотка из провода, длина которого значительно больше диаметра, магнитное поле направлено параллельно оси соленоида и однородно, причём его напряжённость пропорциональна силе тока и (приближённо) числу витков. Внешнее магнитное поле соленоида подобно полю стержневого магнита (см. рис.2).^[1]

Конструктивно длинные соленоиды выполняются в виде однослойной намотки (см. рис. рис.1), так и многослойной.

Если длина намотки значительно превышает её диаметр, то в полости соленоида при подаче в него электрического тока создаётся магнитное поле, близкое к однородному.

Также часто соленоидами называют электромеханические устройствами, исполнительными механизмами, обычно со втягиваемым ферромагнитным сердечником. В таком применении соленоид почти всегда снабжается внешним ферромагнитным магнитопроводом, обычно называемым ярмом.

Соленоид на постоянном токе

Если длина соленоида намного больше его диаметра и не используется магнитный материал, то при протекании тока по обмотке внутри катушки создаётся магнитное поле, направленное вдоль оси, которое однородно и для постоянного тока по величине равно^[2]

${displaystyle B=mu _{0}nI!}$ (СИ),

${displaystyle B={frac {4pi }{c}}nI}$ (СГС),

где ${displaystyle mu _{0}}$ — магнитная проницаемость вакуума,
— число витков на единицу длины соленоида,
— число витков,
— длина соленоида,
— ток в обмотке.

Вследствие того, что две половины бесконечного соленоида в точке их соединения вносят одинаковый вклад в магнитное поле, магнитная индукция полубесконечного соленоида у его края вдвое меньше, чем в объёме. То же самое можно сказать о поле на краях конечного, но достаточно длинного соленоида^[3]:

${displaystyle B_{mathrm {KP} }={frac {1}{2}}mu _{0}nI!}$ (СИ).

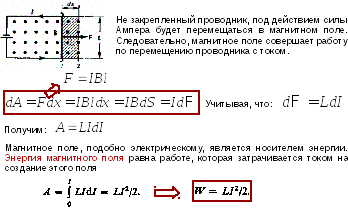
При протекании тока соленоид запасает энергию, равную работе, которую необходимо совершить для установления текущего тока . Величина этой энергии равна

${displaystyle E_{mathrm {coxp} }={{Psi I} over 2}={{LI^{2}} over 2},}$

где — потокосцепление,
— магнитный поток в соленоиде,
— индуктивность соленоида.

При изменении тока в соленоиде возникает ЭДС самоиндукции, значение которой

{displaystyle varepsilon =-L{dI over dt}.}

Индуктивность соленоида

Индуктивность соленоида выражается следующим образом:

${displaystyle L=mu _{0}n^{2}V!={frac {mu _{0}}{4pi }}{frac {z^{2}}{l}}}$

(СИ),

${displaystyle L=4pi n^{2}V!={frac {z^{2}}{l}}}$

(СГС),

где ${displaystyle mu _{0}}$ — магнитная проницаемость вакуума,
— число витков на единицу длины соленоида,
— число витков,
— объём соленоида,
— длина проводника, намотанного на соленоид,
${displaystyle S=pi d^{2}/4}$ — площадь поперечного сечения соленоида,
— длина соленоида,
— диаметр витка.

Без использования магнитного материала магнитная индукция в пределах соленоида является фактически постоянной и равна

${displaystyle B=mu _{0}{frac {N}{l}}I=mu _{0}nI,}$

где — сила тока. Пренебрегая краевыми эффектами на концах соленоида, получим, что потокосцепление через катушку равно магнитной индукции , умноженной на площадь поперечного сечения и число витков :

${displaystyle displaystyle Psi =BSN=mu _{0}N^{2}IS/l=mu _{0}n^{2}VI=LI.}$

Отсюда следует формула для индуктивности соленоида

${displaystyle displaystyle L=mu _{0}N^{2}S/l=mu _{0}n^{2}V,}$

эквивалентная предыдущим двум формулам.

Соленоид на переменном токе

При переменном токе соленоид создаёт переменное магнитное поле. Если соленоид используется как электромагнит, то на переменном токе величина силы притяжения изменяется. В случае якоря из магнитомягкого материала направление силы притяжения не изменяется. В случае магнитного якоря направление силы меняется. На переменном токе соленоид имеет комплексное сопротивление, активная составляющая которого определяется активным сопротивлением обмотки, а реактивная составляющая определяется индуктивностью обмотки.

Применение

Соленоиды постоянного тока чаще всего применяются как поступательный силовой электропривод. В отличие от обычных электромагнитов обеспечивает большой ход. Силовая характеристика зависит от строения магнитной системы (сердечника и корпуса) и может быть близка к линейной.

Соленоиды приводят в движение ножницы для отрезания билетов и чеков в кассовых аппаратах, язычки замков, клапаны в двигателях, гидравлических системах и проч. Один из самых известных примеров — «тяговое реле» автомобильного стартёра.

Соленоиды на переменном токе применяются в качестве индуктора для индукционного нагрева в индукционных тигельных печах.

Примечание

↑ http://www.big-soviet.ru/627/74411/%D0%A1%D0%BE%D0%BB%D0%B5%D0%BD%D0%BE%D0%B8%D0%B4 (БСЭ)
↑ Книга:Савельев И.В.: Электричество и магнетизм. Волны. Оптика.
↑ Книга:Савельев И.В.: Электричество и магнетизм. Волны. Оптика.

См. также

Электромагнетизм
Магнитное поле
Магнит
Электромагнит
Индуктивность
Катушка индуктивности
Катушка Румкорфа

Источник