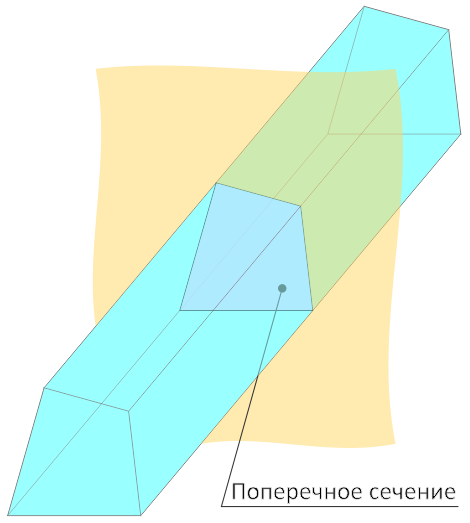
You may encounter situations in which you have a three-dimensional solid shape and need to figure out the area of an imaginary plane inserted through the shape and having borders defined by the boundaries of the solid.
For example, if you had a cylindrical pipe running under your home measuring 20 meters (m) in length and 0.15 m across, you might want to know the cross-sectional area of the pipe.
Cross sections can be perpendicular to the orientation of the axes of the solid if any exist. In the case of a sphere, any cutting plane through the sphere regardless of orientation will result in a disk of some size.
The area of the cross-section depends on the shape of the solid determining the cross-section’s boundaries and the angle between the solid’s axis of symmetry (if any) and the plane that creates the cross section.
Cross-Sectional Area of a Rectangular Solid
The volume of any rectangular solid, including a cube, is the area of its base (length times width) multiplied by its height: V = l × w × h.
Therefore, if a cross section is parallel to the top or bottom of the solid, the area of the cross-section is l × w. If the cutting plane is parallel to one of the two sets the sides, the cross-sectional area is instead given by l × h or w × h.
If the cross-section is not perpendicular to any axis of symmetry, the shape created may be a triangle (if placed through a corner of the solid) or even a hexagon.
Example: Calculate the cross-sectional area of a plane perpendicular to the base of a cube with a volume of 27 m3.
-
Since l = w = h for a cube, any one edge of the cube must be 3 m long (since 3
× 3
× 3 = 27). A cross-section of the type described would therefore be a square 3 m on a side, giving an area of 9 m2.
Cross-Sectional Area of a Cylinder
A cylinder is a solid created by extending a circle through space perpendicular to its diameter. The area of a circle is given by the formula πr2, where r is the radius. It therefore makes sense that the volume of a cylinder would be the area of one of the circles forming its base.
If the cross-section is parallel to the axis of symmetry, then the area of the cross-section is simply a circle with an area of πr2. If the cutting plane is inserted at a different angle, the shape generated is an ellipse. The area uses the corresponding formula: πab (where a is the longest distance from the center of the ellipse to the edge, and b is the shortest).
Example: What is the cross-sectional area of the pipe under your home described in the introduction?
-
This is just πr2 = π(0.15 m)2=
π(0.0225) m2 = 0.071 m2. Note that the length of the pipe is irrelevant to this calculation.
Cross-Sectional Area of a Sphere
Any theoretical plane placed through a sphere will result in a circle (think about this for a few moments). If you know either the diameter or the circumference of the circle the cross-section forms, you can use the relationships C = 2πr and A = πr2 to obtain a solution.
Example: A plane is rudely inserted through the Earth very close to the North Pole, removing a section of the planet 10 m around. What is the cross-sectional area of this chilly slice of Earth?
- Since C = 2πr = 10 m, r = 10/2π = 1.59 m; A = πr2= π(1.59)2= 7.96 m2.
Поперечным сечением называется фигура, образованная пересечением продолговатого тела с воображаемой плоскостью, расположенных перпендикулярно друг другу, т.е. когда тело рассекается строго поперек его длины.
Сечение может иметь простую или сложную форму, а также быть составным.
Площадь и размеры (длина и ширина) поперечного сечения равны соответствующим размерам этой фигуры.
Площадь поперечного сечения
В общем случае, площадь поперечного сечения имеющая сложную или составную форму определяется как сумма (иногда с вычитанием) составляющих ее простых фигур, таких как прямоугольник, треугольник и круг.
Формулы для расчета площади основных фигур.
Пример:
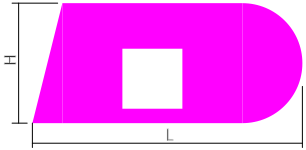
Рассчитать площадь поперечного сечения сложной формы с квадратным отверстием и закруглением.
Для расчета общей площади, сложное сечение раскладывается на простые фигуры:
Прямоугольник — 1, треугольник — 2, полукруг — 3 и прямоугольник — 4, площади которых определяются просто.
В итоге площадь всего поперечного сечения будет получена сложением первых трех фигур с вычитанием фигуры номер 4:
A=A1+A2+A3-A4
Площадь поперечного сечения обозначается латинскими буквами S или A, и измеряется в квадратных единицах длины, например: м2, см2 или мм2.
Площадь составного сечения
Составными называют сечения, которые состоят из двух, трех и более отдельных фигур, не являющихся одним целым.
Это может быть, например сечение балки, состоящее например из швеллера и двух уголков.
Эти сечения сами по себе тоже являются сложными.
Площади поперечного сечения для таких стандартных профилей можно найти в специальном справочнике — сортаменте.
В результате сложив все составляющие профили, получим площадь всего сечения.
Таким образом, расчет площади составного сечения производится аналогично предыдущему порядку, только без вычитаний.
Длина поперечного сечения
Длиной поперечного сечения называют полную (габаритную) длину фигуры как расстояние по горизонтали между двумя её наиболее удаленными точками.
Длина поперечного сечения обозначается латинской буквой L или l и измеряется стандартно в миллиметрах или сантиметрах.
Ширина сечения определяется аналогично, но обозначается буквой H или h.
При решении задач, длину, ширину и площади поперечного сечения рекомендуется переводить соответственно в метры и м2.
Понятие «поперечное сечение» является одним из основных при расчетах на прочность в сопротивлении материалов и технической механике.
Различают два основных вида расчета площади сечений:
- Геометрический — когда требуется найти площадь сечения тела по известным размерам;
- Прочностной — расчет площади поперечного сечения бруса проводится по условию прочности.
Пример расчета поперечных сечений >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Как вычислить площадь поперечного сечения
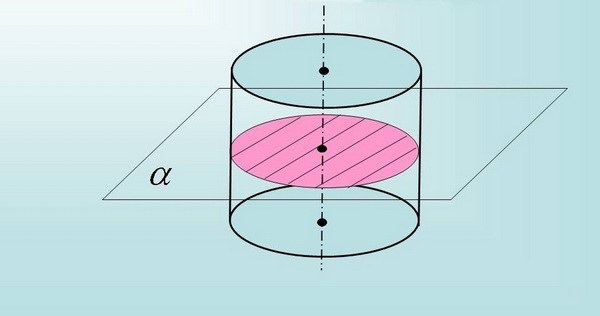
Поперечное сечение образуется под прямым углом по отношению к продольной оси. Причем, сечение разных геометрических фигур представлено может быть различными формами. К примеру, у параллелограмма сечение по внешнему виду напоминает прямоугольник или квадрат, у цилиндра – прямоугольник или круг и т.д.
Вам понадобится
- — калькулятор;
- — исходные данные.
Инструкция
Чтобы найти площадь сечения параллелограмма, нужно знать значение его основания и высоту. Если, к примеру, известна лишь длина и ширина основания, то найдите диагональ, используя для этого теорему Пифагора (квадрат длины гипотенузы в прямоугольном треугольнике равен сумме квадратов катетов: a2 + b2 = c2). Ввиду этого, c = sqrt (a2 + b2).
Найдя значение диагонали, подставьте его в формулу S= c*h, где h – высота параллелограмма. Полученный результат и будет величиной площадью поперечного сечения параллелограмма.
Если же сечение проходит вдоль двух оснований, то его площадь рассчитывайте по формуле: S=a*b.
Для вычисления площади осевого сечения цилиндра, проходящей перпендикулярно основаниям (при условии, что одна сторона этого прямоугольника равна радиусу основания, а вторая – высоте цилиндра), используйте формулу S =2R*h, в которой R – величина радиуса окружности (основания), S – площадь поперечного сечения, а h – высота цилиндра.
Если по условиям задачи сечение не проходит через ось вращения цилиндра, но при этом параллельно его основаниям, значит, сторона прямоугольника не будет равна диаметру окружности основания.
Самостоятельно вычислите неизвестную сторону путем построения окружности основания цилиндра, проведения перпендикуляров от стороны прямоугольника (плоскости сечения) к окружности и расчета размера хорды (по теореме Пифагора). После этого подставьте в S =2а*h полученное значение (2а – значение хорды) и рассчитайте площадь поперечного сечения.
Площадь сечения шара определяется по формуле S = πR2. Обратите внимание на то, что, если расстояние от центра геометрической фигуры до плоскости будет совпадать с плоскостью, то площадь сечения равна будет нулю, потому как шар касается плоскости лишь в одной точке.
Обратите внимание
Дважды пересчитывайте полученный результат: так вы не допустите ошибки в расчетах.
Полезный совет
Чтобы рассчитать площадь сечения любой другой геометрической фигуры, воспользуйтесь математическим справочником, в котором подобраны формулы для расчета и даны подробные рекомендации.
Источники:
- Стереометрия. Теория
- поперечное сечение
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Понятие о геометрических характеристиках однородных поперечных сечений. Центр тяжести; статические моменты; моменты инерции – осевые, центробежный, полярный; моменты сопротивления; радиусы инерции. Главные оси и главные моменты инерции. Понятие об упруго-геометрических характеристиках неоднородных сечений.
2. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПОПЕРЕЧНЫХ СЕЧЕНИЙ
2.1. Некоторые сведения о геометрических характеристиках
Геометрические характеристики – числовые величины (параметры), определяющие размеры, форму, расположение поперечного сечения однородного по упругим свойствам деформируемого элемента конструкции (и, как следствие, характеризующие сопротивление элемента различным видам деформации).
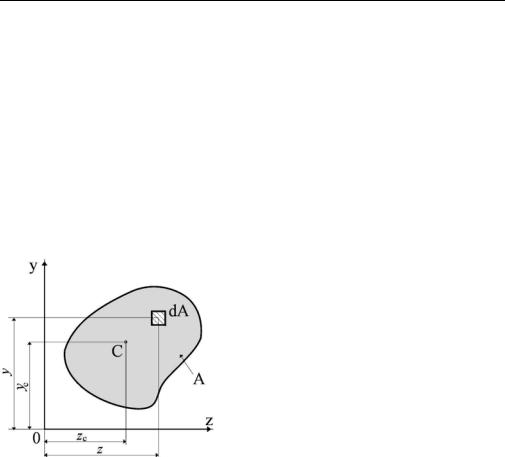
Рассмотрим произвольное поперечное сечение A (сечение бруса) с координатами центра тяжести zc, yc. В точке (z, y) выделим элемент площади dA. Основные геометрические характеристики поперечных сечений элементов конструкций (в том числе и данного сечения) описываются интегралами следующего вида
∫ym zn dA.
A
Рассмотрим некоторые характерные варианты записи этого интеграла и получим выражения для основных геометрических характеристик.
Площадь поперечного сечения
При m=0, n=0 интеграл приобретает вид
∫dA = A ,
A
а соответствующая характеристика, как видим, представляет собой площадь поперечного сечения элемента.
Оказывается, что во многих случаях деформирования тела знание только площади его поперечного сечения недостаточно.
Статические моменты
Если m=1, n=0, тогда получим характеристику
∫y dA = Sz ,
A
которая называется статическим моментом относительно оси z,
или, при m=0, n=1,
∫z dA = Sy
A
статическим моментом относительно оси y.
12
Статический момент относительно данной оси – сумма произведений элементарных площадей dA на их расстояние до данной оси, взятая по всей площади сечения А.
На основании теоремы Вариньяна (из курса теоретической механики) следует, что
|
Sz = ∫y dA =yc A, |
Sy = ∫z dA =zc A, |
|
A |
A |
а для сложного сечения (состоящего из нескольких простых, каждое из кото-
|
рых имеет площадь Ai и координаты собственного центра тяжести yc |
, zс ) |
|
|
i |
i |
|
|
Sz = ∑yci Ai , |
Sy = ∑zci Ai . |
Статический момент относительно какой-либо оси равен произведению всей площади фигуры на расстояние от ее центра тяжести до этой оси.
Отсюда можем получить формулы для определения координат центра тяжести сечения:
|
y = |
Sz |
= ∑yci Ai , |
z |
= |
Sy |
= ∑zci Ai . |
|
c |
A |
∑Ai |
c |
A |
∑Ai |
|
Как видим, относительно осей, проходящих через центр тяжести сечения, статические моменты равны нулю, а сами эти оси называются центральными.
Размерность статических моментов – м3 в системе СИ.
Осевые моменты инерции
Если m=2, n=0, тогда получим характеристику
∫y2 dA = Jz ,
A
которая называется осевым моментом инерции относительно оси z,
или, при m=0, n=2,
∫z2 dA = J y –
A
осевым моментом инерции относительно оси y.
Осевой момент инерции относительно данной оси – сумма произведений элементарных площадей dA на квадрат их расстояний до данной оси, взятая по всей площади сечения А.
Центробежный момент инерции
Если m=1, n=1, тогда получим характеристику
∫z y dA = Jzy ,
A
которая называется центробежным моментом инерции.
13

Центробежный момент инерции относительно осей координат – сумма произведений элементарных площадей dA на их расстояния до этих осей, взятая по всей площади сечения А.
Если хотя бы одна из осей y или z является осью симметрии сечения, центробежный момент инерции такого сечения относительно этих осей равен нулю (так как в этом случае каждой положительной величине z·y·dA можем поставить в соответствие точно такую же, но отрицательную, по другую сторону от оси симметрии сечения, см. рисунок).
Рассмотрим дополнительные геометрические характеристики, которые могут быть получены из перечисленных основных и также часто используются в расчетах на прочность и жесткость.
Полярный момент инерции
Полярным моментом инерции Jp называют характеристику
J p = Jz + J y .
С другой стороны,
J p = Jz + J y = ∫y2 dA +∫z2 dA = ∫(y2 + z2 ) dA = ∫ρ2 dA.
A A A A
Полярный момент инерции (относительно данной точки) – сумма произведений элементарных площадей dA на квадраты их расстояний (ρ2 = y2 + z2 ) до этой точки, взятая по всей площади сечения А.
Размерность моментов инерции – м4 в СИ.
Момент сопротивления Момент сопротивления относительно некоторой оси – величина равная мо-
менту инерции относительно той же оси отнесенному к расстоянию (ymax или zmax) до наиболее удаленной от этой оси точки
|
W = |
J |
z |
; W |
= |
J y |
. |
|
z |
ymax |
y |
zmax |
|||
Размерность моментов сопротивления – м3 в СИ.
Радиус инерции Радиусом инерции сечения относительно некоторой оси, называется величи-
на, определяемая из соотношения:
|
iz = |
J |
z |
, |
iy = |
J y |
. |
|
|
A |
A |
||||||
Радиусы инерции выражаются в м в системе СИ.
Замечание: сечения элементов современных конструкций часто представляют собой некоторую композицию из материалов с разным сопротивлением упругим деформациям, характеризуемым, как известно из курса физики, модулем Юнга E. В самом общем случае неоднородного сечения модуль Юнга является непрерывной функцией координат точек сечения, т. е. E=E(z, y). Поэтому жесткость неоднородного по упругим свойствам сечения
14
характеризуется более сложными, чем геометрические характеристики однородного сечения, характеристиками, а именно упруго-геометрическими вида
∫E (z, y) ym zn dA.
A
2.2. Вычисление геометрических характеристик простых фигур
Прямоугольное сечение
Определим осевой момент инерции прямоугольника относительно оси z.
Разобьем площадь прямоугольника на элементарные площадки с размерами b (ширина) и dy (высота). Тогда площадь такого элементарного прямоугольника (заштрихован) равна dA=b·dy. Подставляя значение dA в первую формулу, получим
|
Jz = ∫y2 dA = +h∫/ 2 y2 b dy =b |
y3 |
+h / 2 = |
b h3 |
. |
||
|
3 |
12 |
|||||
|
A |
−h / 2 |
−h / 2 |
||||
По аналогии запишем
J y = h12b3 .
Подобным образом можно получить геометрические характеристики и для других простых фигур.
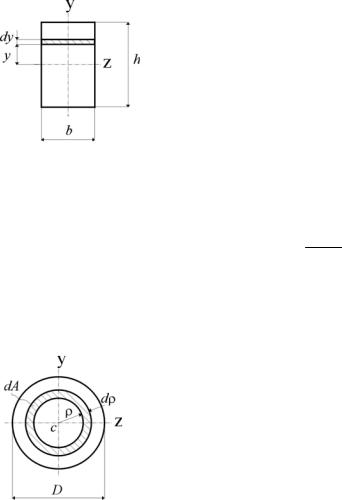
Круглое сечение
Сначала удобно найти полярный момент инерции Jp.
Затем, учитывая, что для круга Jz=Jy, а Jp=Jz+Jy, найдем
Jz=Jy=Jp/2.
Разобьем круг на бесконечно малые кольца толщиной dρ и радиусом ρ; площадь такого кольца dA = 2 π ρ dρ. Подставляя выражение для dA в выражение для Jp и интегрируя,
получим
|
J p = ∫ρ2 dA = D∫/ 2 ρ2 2 π ρ dρ= 2 π |
ρ4 |
D / 2 = |
π D4 |
, |
||||||
|
A |
0 |
4 |
0 |
32 |
||||||
тогда |
J p |
π D4 |
||||||||
|
Jz = J y = |
= |
. |
||||||||
|
2 |
64 |
|||||||||
2.3. Вычисление моментов инерции относительно параллельных осей
Пусть известны моменты инерции произвольного сечения относительно центральных осей z и y:
|
Jz = ∫y2 dA ; |
J y = ∫z2 dA; |
Jzy = ∫z y dA. |
|
A |
A |
A |
15
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Объемные фигуры
Из стереометрии известно, что объемная фигура совершенно любого типа ограничена рядом поверхностей. Например, для таких многогранников, как призма и пирамида, этими поверхностями являются многоугольные стороны. Для цилиндра и конуса речь идет уже о поверхностях вращения цилиндрической и конической фигур.
Вам будет интересно:Что значит слыть: толкование, синонимы
Если взять плоскость и пересечь ею произвольным образом поверхность объемной фигуры, то мы получим сечение. Площадь его равна площади части плоскости, которая будет находиться внутри объема фигуры. Минимальное значение этой площади равно нулю, что реализуется, когда плоскость касается фигуры. Например, сечение, которое образовано единственной точкой, получается, если плоскость проходит через вершину пирамиды или конуса. Максимальное значение площади сечения зависит от взаимного расположения фигуры и плоскости, а также от формы и размеров фигуры.
Ниже рассмотрим, как рассчитывать площади образованных сечений для двух фигур вращения (цилиндр и конус) и двух полиэдров (пирамида и призма).
Расчет
Вычислить число витков, зная конструкцию, можно по формуле нахождения энергии и ее магнитного поля W = LI2/2, где L является индукцией, I — силой тока. Витки находятся из формулы L/d, где d является проводным диаметром. Стоит указать, что есть специальный калькулятор, в который нужно только подставить необходимые параметры. При этом можно определить, однослойный или многослойный проводник.
С сердечником
Стоит отметить, что со стержнем, намоткой, обмоткой индукция вычисляется через замкнутый магнитный поток индуктивных элементов, в то время как без него учитывается поток, который пронизывает только проводник с токовой энергией. Расчитывая индуктивность подобных элементов, необходимо учесть размеры и материал центральной части. Обобщенно можно представить формулу схематично. При этом требуется взять в расчет источник с сопротивлением магнитной цепи, абсолютной магнитной проницаемостью вещества, площадью поперечного сердечникового сечения и длиной средней силовой линии. Зная это, можно посчитать индукцию. Стоит учитывать погрешность. Она будет равна 25%.
Вам это будет интересно Определение резонанса
Без сердечника
Стоит указать, что без ферритового, геометрического и цилиндрического сердечника с мощным каркасом источник имеет небольшую индукцию, а с ним она повышается. Это связано с тем, что имеется материальная магнитная проницаемость. Форма бывает разная. Есть броневой, стержневой и тороидальный материал.
Обратите внимание! Рассчитать можно, используя метод эллиптических максвелловских интегралов и специальную онлайн программу.
Катушка — незаменимый компонент любой электросети, который имеет вид скрученного или обвивающего элемента с проводником. Влияет на ее индукцию число проводных витков, площадь сечения, длина и материал сердечника. Отыскать количество витков и посчитать индуктивность с сердечником и без него несложно, главное — руководствоваться приведенными выше рекомендациями.
Цилиндр
Круговой цилиндр является фигурой вращения прямоугольника вокруг любой из его сторон. Цилиндр характеризуется двумя линейными параметрами: радиусом основания r и высотой h. Ниже схематически показано, как выглядит круговой прямой цилиндр.
Для этой фигуры существует три важных типа сечения:
- круглое;
- прямоугольное;
- эллиптическое.
Эллиптическое образуется в результате пересечения плоскостью боковой поверхности фигуры под некоторым углом к ее основанию. Круглое является результатом пересечения секущей плоскости боковой поверхности параллельно основанию цилиндра. Наконец, прямоугольное получается, если секущая плоскость будет параллельна оси цилиндра.
Площадь круглого сечения рассчитывается по формуле:
S1 = pi*r2
Площадь осевого сечения, то есть прямоугольного, которое проходит через ось цилиндра, определяется так:
S2 = 2*r*h
Формула площади треугольника по длинам всех сторон
S = p ⋅ ( p − a ) ⋅ ( p − b ) ⋅ ( p − c ) S= sqrt{pcdot(p-a)cdot (p-b)cdot (p-c)} S=p⋅(p−a)⋅(p−b)⋅(p−c) ,
a , b , c a, b, c a,b,c — длины сторон треугольника; p p p — половина суммы всех сторон треугольника (то есть, половина периметра треугольника):
p = 1 2 ( a + b + c ) p=frac{1}{2}(a+b+c) p=21(a+b+c)
Эта формула называется формулой Герона.
Пример
Найти площадь треугольника, если известны длины трех его сторон, равные 3 (см.), 4 (см.), 5 (см.).
Решение
a = 3 a=3 a=3 b = 4 b=4 b=4 c = 5 c=5 c=5
Найдем половину периметра p p p:
p = 1 2 ( 3 + 4 + 5 ) = 1 2 ⋅ 12 = 6 p=frac{1}{2}(3+4+5)=frac{1}{2}cdot 12=6 p=21(3+4+5)=21⋅12=6
Тогда, по формуле Герона, площадь треугольника:
S = 6 ⋅ ( 6 − 3 ) ⋅ ( 6 − 4 ) ⋅ ( 6 − 5 ) = 36 = 6 S=sqrt{6cdot(6-3)cdot(6-4)cdot(6-5)}=sqrt{36}=6 S=6⋅(6−3)⋅(6−4)⋅(6−5) =36 =6 (см. кв.)
Ответ: 6 (см. кв.)
Сечения конуса
Конусом является фигура вращения прямоугольного треугольника вокруг одного из катетов. Конус имеет одну вершину и круглое основание. Его параметрами также являются радиус r и высота h. Пример конуса, сделанного из бумаги, показан ниже.
Видов конических сечений существует несколько. Перечислим их:
- круглое;
- эллиптическое;
- параболическое;
- гиперболическое;
- треугольное.
Они сменяют друг друга, если увеличивать угол наклона секущей плоскости относительно круглого основания. Проще всего записать формулы площади сечения круглого и треугольного.
Круглое сечение образуется в результате пересечения конической поверхности плоскостью, которая параллельна основанию. Для его площади справедлива следующая формула:
S1 = pi*r2*z2/h2
Здесь z — это расстояние от вершины фигуры до образованного сечения. Видно, что если z = 0, то плоскость проходит только через вершину, поэтому площадь S1 будет равна нулю. Поскольку z
Треугольное получается, когда плоскость пересекает фигуру по ее оси вращения. Формой получившегося сечения будет равнобедренный треугольник, сторонами которого являются диаметр основания и две образующие конуса. Как находить площадь сечения треугольного? Ответом на этот вопрос будет следующая формула:
S2 = r*h
Это равенство получается, если применить формулу для площади произвольного треугольника через длину его основания и высоту.
Площадь поперечного сечения
В общем случае, площадь поперечного сечения имеющая сложную или составную форму определяется как сумма (иногда с вычитанием) составляющих ее простых фигур, таких как прямоугольник, треугольник и круг.
Формулы для расчета площади основных фигур.
Пример: Рассчитать площадь поперечного сечения сложной формы с квадратным отверстием и закруглением. Для расчета общей площади, сложное сечение раскладывается на простые фигуры:
Прямоугольник — 1, треугольник — 2, полукруг — 3 и прямоугольник — 4, площади которых определяются просто. В итоге площадь всего поперечного сечения будет получена сложением первых трех фигур с вычитанием фигуры номер 4:
A=A1+A2+A3-A4
Площадь поперечного сечения обозначается латинскими буквами S или A, и измеряется в квадратных единицах длины, например: м2, см2 или мм2.
Площадь составного сечения
Составными называют сечения, которые состоят из двух, трех и более отдельных фигур, не являющихся одним целым. Это может быть, например сечение балки, состоящее например из швеллера и двух уголков.
Эти сечения сами по себе тоже являются сложными. Площади поперечного сечения для таких стандартных профилей можно найти в специальном справочнике — сортаменте.
В результате сложив все составляющие профили, получим площадь всего сечения.
Таким образом, расчет площади составного сечения производится аналогично предыдущему порядку, только без вычитаний.
Сечения призмы
Призма — это большой класс фигур, которые характеризуются наличием двух одинаковых параллельных друг другу многоугольных оснований, соединенных параллелограммами. Любое сечение призмы — это многоугольник. В виду разнообразия рассматриваемых фигур (наклонные, прямые, n-угольные, правильные, вогнутые призмы) велико и разнообразие их сечений. Далее рассмотрим лишь некоторые частные случаи.
Если секущая плоскость параллельна основанию, то площадь сечения призмы будет равна площади этого основания.
Если плоскость проходит через геометрические центры двух оснований, то есть является параллельной боковым ребрам фигуры, тогда в сечении образуется параллелограмм. В случае прямых и правильных призм рассматриваемый вид сечения будет представлять собой прямоугольник.
Онлайн-калькулятор
Треугольники бывают различных видов. Например, существует равносторонний треугольник (тот, у которого все стороны равны), равнобедренный (в нем равны две стороны) и прямоугольный (в котором один из углов прямой, т. е. равен 90 градусам).
Площадь треугольника можно найти различными способами в зависимости от того, какие элементы фигуры известны по условию задачи, будь то углы, длины, либо же вообще радиусы окружностей, связанных с треугольником. Рассмотрим каждый способ отдельно с примерами.
Формула площади треугольника по одной стороне и двум углам
S = a 2 2 ⋅ sin β sin γ sin ( β + γ ) S=frac{a^2}{2}cdot frac{sin{beta}sin{gamma}}{sin(beta+gamma)} S=2a2⋅sin(β+γ)sinβsinγ,
a a a — длина стороны треугольника; β , γ beta, gamma β,γ — углы, прилежащие к стороне a a a.
Пример
Дано сторону треугольника, равную 10 (см.) и два прилежащих к ней угла по 30 градусов. Найти площадь треугольника.
Решение
a = 10 a=10 a=10 β = 3 0 ∘ beta=30^{circ} β=30∘ γ = 3 0 ∘ gamma=30^{circ} γ=30∘
По формуле:
S = 1 0 2 2 ⋅ sin 3 0 ∘ sin 3 0 ∘ sin ( 3 0 ∘ + 3 0 ∘ ) = 50 ⋅ 1 2 3 ≈ 14.4 S=frac{10^2}{2}cdot frac{sin{30^{circ}}sin{30^{circ}}}{sin(30^{circ}+30^{circ})}=50cdotfrac{1}{2sqrt{3}}approx14.4 S=2102⋅sin(30∘+30∘)sin30∘sin30∘=50⋅23 1≈14.4 (см. кв.)
Ответ: 14.4 (см. кв.)
Формула площади треугольника по трем сторонам и радиусу описанной окружности
S = a ⋅ b ⋅ c 4 R S=frac{acdot bcdot c}{4R} S=4Ra⋅b⋅c,
a , b , c a, b, c a,b,c — стороны треугольника; R R R — радиус описанной окружности вокруг треугольника.
Пример
Числа возьмем из второй нашей задачи и добавим к ним радиус R R R окружности. Пусть он будет равен 10 (см.).
Решение
a = 3 a=3 a=3 b = 4 b=4 b=4 c = 5 c=5 c=5 R = 10 R=10 R=10
S = 3 ⋅ 4 ⋅ 5 4 ⋅ 10 = 60 40 = 1.5 S=frac{3cdot 4cdot 5}{4cdot 10}=frac{60}{40}=1.5 S=4⋅103⋅4⋅5=4060=1.5 (см. кв.)
Ответ: 1.5 (см.кв.)
Формула площади треугольника по двум сторонам и углу между ними
S = 1 2 ⋅ b ⋅ c ⋅ sin ( α ) S=frac{1}{2}cdot bcdot ccdotsin(alpha) S=21⋅b⋅c⋅sin(α),
b , c b, c b,c — стороны треугольника;
α alpha α — угол между сторонами b b b и c c c.
Пример
Стороны треугольника равны 5 (см.) и 6 (см.), угол между ними равен 30 градусов. Найти площадь треугольника.
Решение
b = 5 b=5 b=5 c = 6 c=6 c=6 α = 3 0 ∘ alpha=30^{circ} α=30∘
S = 1 2 ⋅ 5 ⋅ 6 ⋅ sin ( 3 0 ∘ ) = 7.5 S=frac{1}{2}cdot 5cdot 6cdotsin(30^{circ})=7.5 S=21⋅5⋅6⋅sin(30∘)=7.5 (см. кв.)
Ответ: 7.5 (см. кв.)
Контрольная по геометрии недорого на сервисе Студворк от профильных экспертов!
Формула площади треугольника по трем сторонам и радиусу вписанной окружности
S = p ⋅ r S=pcdot r S=p⋅r,
p p p — половина периметра треугольника:
p = a + b + c 2 p=frac{a+b+c}{2} p=2a+b+c,
a , b , c a, b, c a,b,c — стороны треугольника; r r r — радиус вписанной в треугольник окружности.
Пример
Пусть радиус вписанной окружности равен 2 (см.). Длины сторон возьмем из предыдущей задачи.
Решение
a = 3 a=3 a=3 b = 4 b=4 b=4 c = 5 c=5 c=5 r = 2 r=2 r=2
p = 3 + 4 + 5 2 = 6 p=frac{3+4+5}{2}=6 p=23+4+5=6
S = 6 ⋅ 2 = 12 S=6cdot 2=12 S=6⋅2=12 (см. кв.)
Ответ: 12 (см. кв.)