Эллипс — это геометрическая фигура, которая образуется в результате пересечения кругового цилиндра плоскостью.
Онлайн-калькулятор площади эллипса
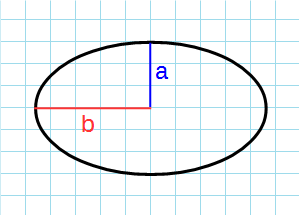
Уравнение эллипса выглядит следующим образом:
x2a2+y2b2=1frac{x^2}{a^2}+frac{y^2}{b^2}=1
aa — это большая полуось эллипса, а bb, соответственно, малая полуось. Кроме этого, у эллипса есть точки на большой полуоси, которые называются фокусами. А расстояние между этими точками называется фокусным. Эти величины связаны между собой одним соотношением:
a2=b2+c2a^2=b^2+c^2,
где cc это половина расстояние между фокусами.
Эта формула оказывается очень полезной при решении различных задач, когда, например, какая-либо величина из трех неизвестна.
Окружность является частным случаем эллипса. Это имеет место тогда, когда большая и малая полуоси совпадают. Они равны радиусу окружности.
Существует еще одна, общая, запись уравнения эллипса:
Ax2+Bxy+Cy2=1Ax^2+Bxy+Cy^2=1
A,B,CA, B, C — для каждого эллипса это постоянные числа.
Перейдем к рассмотрению задач, направленных на нахождение площади эллипса.
Формула площади эллипса через каноническое уравнение
Формула для нахождения площади в этом случае такова:
S=π⋅a⋅bS=picdot acdot b
a,ba, b — большая и мала полуоси эллипса, соответственно.
Решим задачу этим способом.
Дано уравнение эллипса. Найти его площадь и округлить ответ до целого числа.
x225+y29=1frac{x^2}{25}+frac{y^2}{9}=1
Решение
a2=25a^2=25
b2=9b^2=9
Для начала найдем длины наших полуосей:
a=a2=25=5a=sqrt{a^2}=sqrt{25}=5
b=b2=9=3b=sqrt{b^2}=sqrt{9}=3
Вычислим площадь:
S=π⋅a⋅b=π⋅5⋅3≈47S=picdot acdot b=picdot 5cdot 3approx47 (см. кв.)
Ответ: 47 см. кв.
Формула площади эллипса через общее (неканоническое) уравнение
S=2⋅π4⋅A⋅C−B2S=frac{2cdotpi}{sqrt{4cdot Acdot C-B^2}}
A,B,CA, B, C — коэффициенты в общем уравнении эллипса.
Эллипс задан уравнением:
10×2+8xy+1.7y2=110x^2+8xy+1.7y^2=1
Найти площадь фигуры.
Решение
A=10A=10
B=8B=8
C=1.7C=1.7
S=2⋅π4⋅A⋅C−B2=2⋅π4⋅10⋅1.7−82≈3.14S=frac{2cdotpi}{sqrt{4cdot Acdot C-B^2}}=frac{2cdotpi}{sqrt{4cdot 10cdot 1.7-8^2}}approx3.14 (см. кв.)
Ответ: 3.14 см. кв.
Вам нужно решение для контрольной работы по геометрии? Наши эксперты помогут вам с решением!
Тест по теме «Площадь эллипса»
Загрузить PDF
Загрузить PDF
Эллипс — это фигура на плоскости, которая похожа на приплюснутый круг. Формула для нахождения площади эллипса напоминает выражение для площади круга. При этом следует помнить, что у эллипса два важных параметра: большая полуось и малая полуось.
-
1
Определите большую полуось эллипса. Это расстояние от центра эллипса до его самого дальнего края. Большую полуось можно представить себе в качестве максимального радиуса эллипса. Измерьте длину большой полуоси или найдите ее значение в условии задачи. Обозначим эту длину буквой a.
- Большая полуось эллипса является максимальным расстоянием от его центра до края.[1]
- Большая полуось эллипса является максимальным расстоянием от его центра до края.[1]
-
2
Определите малую полуось эллипса. Как можно догадаться по названию, это кратчайшее расстояние от центра эллипса до его края. Обозначим это расстояние латинской буквой b.
- Малая полуось эллипса расположена под прямым углом 90º к его большой полуоси, однако для нахождения площади нет необходимости определять углы.
- Малая полуось эллипса является минимальным расстоянием от его центра до края.
-
3
Умножьте на число «пи». Площадь эллипса равна a x b x π. Поскольку перемножаются две величины с размерностью длины, в ответе получится длина в квадрате.
- Например, если большая полуось эллипса равна 5 единицам, а малая 3 единицам длины, то получим площадь 5 x 3 x π, или около 47 квадратных единиц длины.
- Если у вас нет под рукой калькулятора или на калькуляторе нет символа π, используйте вместо этого числа значение «3,14».
Реклама
-
1
Вспомните формулу для площади круга. Вероятно, вы помните, что площадь круга равна πr2, то есть π x r x r. Что, если мы попробуем найти площадь круга по формуле для эллипса? В этом случае следует измерить радиус в одном направлении: r. Измерим радиус в перпендикулярном направлении, и тоже получим r. Подставим в формулу для площади эллипса: π x r x r! Таким образом, круг является лишь отдельной разновидностью эллипса.[2]
-
2
Представьте, что круг сплющили. Вообразите, что круг сжали до формы эллипса. По мере сжатия один радиус круга будет становиться все короче, а второй — длиннее. При этом площадь круга будет оставаться неизменной, поскольку ничто не покидает его и не добавляется к нему.[3]
Если мы используем в формуле для площади короткий и длинный радиусы, то «сплющивание» и «расширение» уравновесят друг друга, и в результате получится правильный ответ.Реклама
Советы
- Если вам требуется строгое доказательство, его можно получить с помощью интегрирования.[4]
Реклама
Об этой статье
Эту страницу просматривали 33 956 раз.
Была ли эта статья полезной?
Как рассчитать площадь эллипса
На данной странице калькулятор поможет рассчитать площадь эллипса онлайн. Для расчета задайте длину полуосей.
Эллипс – замкнутая овальная кривая, обладающая тем свойством, что сумма расстояний каждой её точки от двух данных точек (фокусов) остаётся постоянной.
Через оси
a:
b:
Результат
Ответы:
Формула для нахождения площади эллипса через полуоси:
π — константа равная (3.14); a — малая полуось; b — большая полуось.
На этой странице вы сможете рассчитать площадь эллипса. Для этого необходимо знать длины полуосей или осей — просто введите их в поля калькулятора и получите результат. Кроме этого вы можете найти площадь эллипса самостоятельно по формулам, которые мы также публикуем на этой странице.
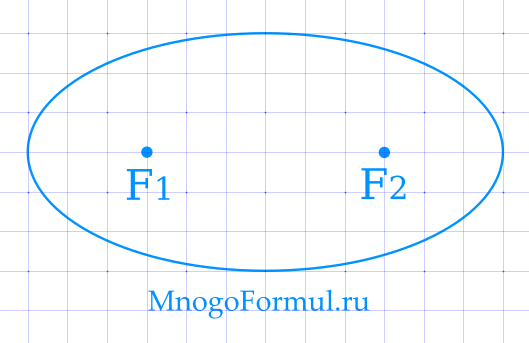
Эллипс — замкнутая кривая на плоскости, которую можно получить пересечением цилиндра плоскостью.
Эллипс можно определить как замкнутую плоскую кривую, сумма расстояний от каждой точки которой до двух точек F1 и F2 равна постоянной величине. Точки F1 и F2 называют фокусами эллипса.
Формула площади эллипса через полуоси
S = pi Rr
R — большая полуось эллипса
r — малая полуось эллипса
Формула площади эллипса через оси
S= pi dfrac{dD}{4}
D — большая ось эллипса
d — малая ось эллипса
Эллипс— это пересечение плоскости и кругового цилиндра.
Поскольку в участии при графическом создании эллипса задействованы два радиуса окружностей – малый и большой, или как их еще называют для эллипса – малая и большая полуоси, то естественно они участвуют и при подсчете площади.
Окружность является частным случаем эллипса. Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой.
Площадь эллипса – это часть поверхности, которая ограничена замкнутыми линиями этой фигуры.

Наш онлайн калькулятор высчитывает площадь при помощи значений большой и малой полуоси фигуры.
Формула, по которой вычисляется площадь эллипса:
Где пи – это постоянное число 3.1415, а — обозначает значение большой полуоси, b— является длиной малой полуоси.
К Вашему вниманию анимация на тему как нарисовать эллипс.